A inteligência artificial dominou dados tabulares, sequenciais e em grade. Planilhas, texto, imagens. Todas estas formas de informação são bem trabalhadas pelo conjunto de algoritmos de aprendizagem de máquina que acabamos colocando sobre o termo inteligência artificial. Contudo, a observadora leitora deve ser capaz de perceber que o mundo real é relacional. Pessoas se conectam à outras pessoas, animais e objetos. Átomos se ligam para formar moléculas. Cidades conectam-se por estradas. Até mesmo os neurônios do seu cérebro se conectam entre si. Usuários compram produtos, e produtos são comprados por usuários. Todas estas relações formam redes grandes e complexas que definem o tecido do universo em que vivemos.
“As redes são o pré-requisito para descrever qualquer sistema complexo, indicando que a teoria da complexidade deve inevitavelmente apoiar-se nos ombros da teoria das redes.” - Albert-László Barabási 1
Estas redes não são apenas coleções de números ou sequências. Elas têm estrutura, contexto e significado. Considere as redes sociais, nas quais, cada usuário é um nó desta rede e cada amizade é uma conexão. Ou a distribuição de energia elétrica na sua cidade. Neste caso, sua casa é um nó com uma conexão, enquanto uma sub-estação é um nó com milhares de conexões.
No mundo real, físico e estruturante, podemos considerar que as moléculas são intrinsecamente redes. Neste caso, cada átomo é um nó, com identidade e características próprias e particulares, tais como peso atômico e carga. Nesta rede molecular, cada ligação química é uma conexão que define a relação, e a força entre eles. A maneira específica como esses átomos se conectam, formando a topologia da rede molecular, não é aleatória e dita a forma tridimensional da molécula, suas propriedades farmacológicas, seu papel em reações bioquímicas ou suas características como material.
As redes que definem a trama do universo são complexas e, muitas vezes, dinâmicas. Elas não podem ser tratadas como tabelas ou sequências. Precisamos de uma nova abordagem para entender e aprender a partir desses dados e suas relações. Esta abordagem é a teoria dos grafos.
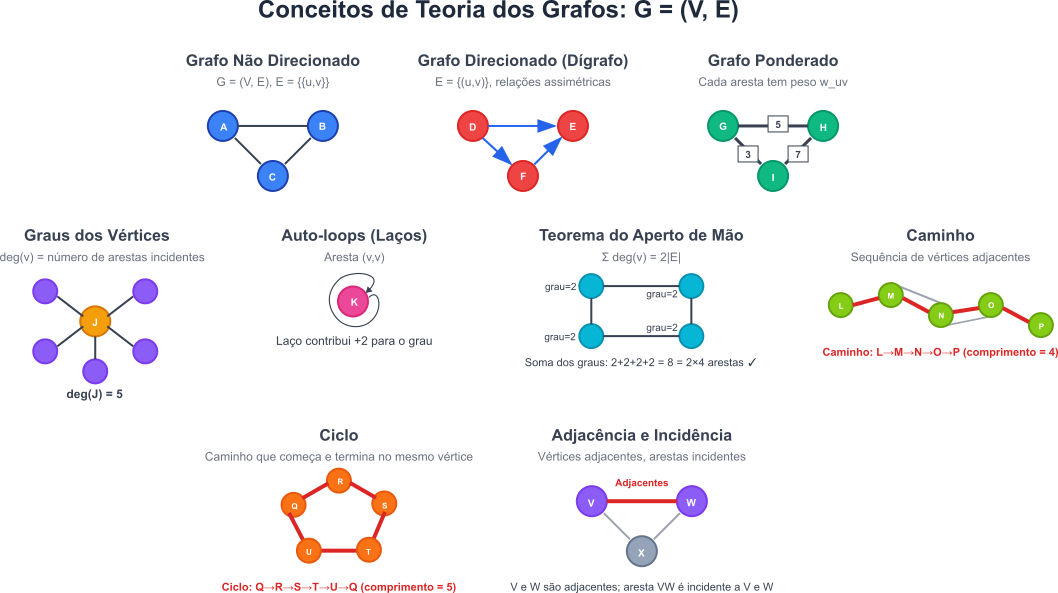
Até este ponto, a atenta leitora leu sobre redes, vértices e conexões. Agora precisamos formalizar isso matematicamente. Vamos definir o que é um grafo, como representá-lo e por que ele é tão importante.
Um grafo, em sua essência matemática, é uma estrutura usada para modelar relações entre objetos. Formalmente, um grafo $G$ será definido como uma tupla dada por $G = (V, E)$, onde $V$ será um conjunto de vértices, que anteriormente chamamos de vértices, e $E$ será um conjunto de arestas, que chamamos de conexões, mas que em muitos livros são chamados de links. Ou seja:
Vértices: são as unidades fundamentais de um grafo, representando entidades, objetos ou conceitos. Por exemplo, em uma rede social, os vértices podem representar usuários individuais; em uma molécula, os vértices podem representar átomos.
Arestas: representam as relações ou conexões entre pares de vértices. Uma aresta $e \in E$ será tipicamente associada a um par de vértices. Por exemplo, em uma rede social, uma aresta pode significar uma relação de amizade ou um seguidor.
Os grafos podem ser classificados com base na natureza de suas arestas:
Grafos Direcionados (Dígrafos): nestes grafos as arestas possuem uma direção, indicando um fluxo ou uma relação assimétrica. Se uma aresta conecta o vértice $u$ ao vértice $v$, ela será representada como um par ordenado $(u,v)$, significando que a relação vai de $u$ para $v$. Um exemplo é a relação “segue” no X, onde um usuário $A$ pode seguir o usuário $B$, mas $B$ não necessariamente segue $$A$. A matriz de adjacência de um dígrafo pode não ser simétrica.
Grafos Não Direcionados: nestes grafos as arestas não possuem direção, representando relações simétricas. Se uma aresta conecta os vértices $u$ e $v$, ela é representada como um par não ordenado ${u,v}$. Um exemplo é uma amizade no Facebook, onde a relação é mútua.A matriz de adjacência de um grafo não direcionado é simétrica.
A atenta leitora notou a diferença na notação: $(u,v)$ para grafos direcionados e ${u,v}$ para grafos não direcionados. Essa diferença é importante, pois reflete a natureza da relação entre os vértices.
Além disso, as arestas podem ter pesos:
Existem alguns termos relacionados à conectividade que precisam ser destacados :
Adjacência: dois vértices são ditos adjacentes se existe uma aresta conectando-os diretamente.
Incidência: uma aresta é dita incidente aos vértices que ela conecta
Grau de um Vértice:
em um grafo não direcionado, o grau de um vértice $v$, denotado por $d(v)$ ou $deg(v)$, é o número de arestas incidentes a ele.
Em um grafo direcionado, distinguimos o grau de entrada, número de arestas que chegam ao vértices, do grau de saída, número de arestas que partem do vértices.
Um laço, do inglês auto-loop, é uma aresta que conecta um vértice a si mesmo, $(v,v)$. Em algumas convenções, um laço contribui com 2 para o grau do vértice para manter a consistência com teoremas como o teorema do aperto de mão. A soma dos graus é duas vezes o número de arestas.
O Teorema do Aperto de Mão
Em qualquer grafo $G = (V, E)$, a soma dos graus de todos os vértices é igual ao dobro do número de arestas:
\[\sum_{v \in V} \deg(v) = 2|E|\]Este teorema revela uma propriedade estrutural fundamental de todos os grafos, conectando vértices individuais à estrutura global.
Na prática, isso significa que este teorema permite verificar se um conjunto de dados representa um grafo válido. Se a soma dos graus for ímpar, não pode haver um grafo correspondente. Isso é útil em várias aplicações: Além disso, o teorema do aperto de mão fornece informações sobre a conectividade e a estrutura do grafo, como a presença de vértices isolados ou componentes desconexos. Isso pode ser útil em aplicações práticas, como redes sociais, onde a conectividade entre usuários é importante.
Lembre-se: o número de vértices com grau ímpar é sempre par
A intuitiva leitora pode considerar uma festa em que cada pessoa é um vértice. Como em uma festa as pessoas educadas se cumprimentam, cada aperto de mão envolve exatamente duas pessoas, então a soma de apertos individuais é sempre o dobro do número total de cumprimentos.
Exemplo: No nosso grafo ciclo de $4$ vértices, cada nó tem grau $2$, então:
\[\sum \deg(v) = 2 + 2 + 2 + 2 = 8 = 2 \times 4 \text{ arestas}\]
Caminho: uma sequência de vértices onde cada par consecutivo é adjacente. O comprimento do caminho é o número de arestas.
Ciclo: um caminho que começa e termina no mesmo vértice, sem repetir arestas ou vértices, exceto o inicial/final. O comprimento do ciclo é o número de arestas.
A curiosa leitora pode deleitar-se com estes conceitos de forma gráfica na Figura 1.

Figura 1: Conceitos de Grafos
Para que a esforçada leitora, e eu, possamos usar um computador para representar grafos e aplicar a estes algoritmos como as GNNs, tema deste capítulo, os grafos precisarão ser representados numericamente. Neste caso, as representações matriciais são comuns e, muitas vezes, fundamentais.
Matriz de Adjacência ($A$): para um grafo com $N = \vert V \vert$ vértices, a matriz de adjacência $A$ será uma matriz $N\times N$ na qual a entrada $A_{ij}$ descreverá a conexão entre o vértice $i$ e o vértice $j$. Neste caso, $A_{ij}$ será definido como:
para grafos não ponderados: $A_{ij} = 1$ se existe uma aresta entre o vértices $i$ e o vértices $j$, e $A_{ij} = 0$ caso contrário.
para grafos ponderados: $A_{ij}=w_{ij}$, o peso da aresta, se existe uma aresta entre $i$ e $j$, e $A_{ij} = 0$ caso contrário.
se o grafo é não direcionado, $A$ é uma matriz simétrica. Tal que: $A_{ij}=$A_{ji}$.
#### Exemplo 1: Matriz de Adjacência
Considere um grafo não direcionado e não ponderado com $V = {1,2,3,4}$ e arestas $E = { {1,2}, {1,3}, {2,3}, {3,4} }$. A matriz de adjacência $A$ será:
\[A = \begin{array}{c|cccc} & 1 & 2 & 3 & 4 \\ \hline 1 & 0 & 1 & 1 & 0 \\ 2 & 1 & 0 & 1 & 0 \\ 3 & 1 & 1 & 0 & 1 \\ 4 & 0 & 0 & 1 & 0 \end{array}\]Neste exemplo, cada linha e cada coluna representam um vértice, e a entrada $A_{ij}$ é $1$ se existe uma aresta entre os vértices $i$ e $j$, e $0$ caso contrário. Assim, o vértice $1$ está conectado ao vértice $2$$ e ao vértice $3$, mas não ao vértice $4$.
Matriz de Grau (D): a matriz de grau $D$ é uma matriz diagonal $N \times N$ onde cada elemento diagonal $D_{ii}$ é o grau do vértice $i$. Para grafos não ponderados, $D_{ii} = \sum_j A_{ij}$. Todos os elementos fora da diagonal são zero.
#### Exemplo 2: Matriz de Grau
Continuando com o grafo $V = {1,2,3,4}$ e arestas $E = { {1,2}, {1,3}, {2,3}, {3,4} }$ que usamos no exemplo 1, o grau de cada vértice será:
Sendo assim, a matriz de grau $D$ será dada por:
\[D = \begin{array}{c|cccc} & 1 & 2 & 3 & 4 \\ \hline 1 & 2 & 0 & 0 & 0 \\ 2 & 0 & 2 & 0 & 0 \\ 3 & 0 & 0 & 3 & 0 \\ 4 & 0 & 0 & 0 & 1 \end{array}\]Matriz de Características ($X$ ou $H$): a matriz de características $X$ (ou $H$ para representações ocultas) é uma matriz $N \times F$, onde $N$ é o número de vértices e $F$ é o número de características (atributos) associadas a cada vértice. Cada linha $X_i$ (ou $H_i$) é o vetor de características do vértice $i$. Essas características podem ser informações estruturais, como o grau do vértice ou atributos específicos do domínio. Por exemplo, informações de perfil de usuário em uma rede social, ou propriedades de átomos em uma molécula.
#### Exemplo Numérico 1.2.3: Matriz de Características**
Continuando com o grafo $V = {1,2,3,4}$ e arestas $E = { {1,2}, {1,3}, {2,3}, {3,4} }$ que usamos no exemplo 1, vamos supor que cada vértice tenha $F = 2$ características dadas por:
A matriz de características $X$ é:
\[X = \begin{array}{c|cc} & f_1 & f_2 \\ \hline 1 & 0.5 & 0.2 \\ 2 & 0.1 & 0.8 \\ 3 & 0.9 & 0.3 \\ 4 & 0.4 & 0.6 \end{array}\]No contexto de redes neurais representações ocultas referem-se aos vetores de características aprendidos pelas camadas intermediárias, do inglês: hidden layers, da rede neural. Especificamente:
- $X$: matriz de características iniciais ou de entrada - contém os atributos originais dos vértices do grafo
- $H$: matriz de representações ocultas - contém os vetores de características processados e aprendidos pelas camadas da GNN
Durante o processo de aprendizado de uma GNN:
- A rede inicia com as características originais $X$
- Cada camada transforma essas características, incorporando informações da estrutura do grafo e dos vértices vizinhos
- As saídas das camadas intermediárias são as “representações ocultas” $H^{(l)}$, onde $l$ indica a camada
- Essas representações capturam padrões mais complexos e abstratos que não estavam explícitos nas características originais
A escolha entre representações matriciais não é meramente uma decisão de armazenamento de dados. A representação escolhida irá moldar a arquitetura das GNNs que construiremos.
A atenta leitora deve observar qua a matriz de adjacência informa diretamente como a informação dos vizinhos é acessada. Enquanto as matrizes de grau são cruciais para técnicas de normalização para estabilizar o aprendizado. Finalmente, as matrizes de características definem o estado inicial dos vértices a partir do qual as GNNs aprendem. As limitações dessas representações, por exemplo, a densidade da matriz de adjacência para grafos grandes, impulsionam a pesquisa em abordagens mais escaláveis.
Outras representações importantes, embora menos relacionadas com nosso objetivo de estudo, incluem:
A tabela abaixo resume as notações comuns usadas na teoria dos grafos e nas GNNs:
Tabela 1: Notações Comuns em Grafos
| Símbolo | Descrição | Forma Matemática/Exemplo (se aplicável) |
|---|---|---|
| $G$ | Grafo | $G = (V, E)$ |
| $V$ | Conjunto de Vértices | ${v_1, v_2, \ldots, v_N}$ |
| $E$ | Conjunto de Arestas | ${{u,v} \mid u,v \in V}$ ou ${(u,v) \mid u,v \in V}$ |
| $N$ | Número de vértices | $|V|$ |
| $M$ | Número de Arestas | $|E|$ |
| $A$ | Matriz de Adjacência | Matriz $N \times N$, $A_{ij} = 1$ se $(i,j) \in E$ (não ponderado) |
| $X$ ou $H$ | Matriz de Características dos vértices | Matriz $N \times F$ |
| $F$ | Número de Características dos vértices | Inteiro positivo |
| $D$ | Matriz de Grau | Matriz diagonal $N \times N$, $D_{ii} = \deg(i)$ |
| $L$ | Laplaciana do Grafo | $L = D - A$ |
| $\mathcal{N}(v)$ | Vizinhança do vértice $v$ | ${u \mid (v,u) \in E}$ |
| $w_{uv}$ | Peso da aresta $(u,v)$ | Escalar |
####################################Parei aqui####################################
A aplicação direta de arquiteturas de redes neurais tradicionais, como Redes Neurais Convolucionais (CNNs) ou Redes Neurais Recorrentes (RNNs), a dados em grafos apresenta desafios significativos:
Esses desafios motivaram o desenvolvimento de Redes Neurais em Grafos, que são projetadas especificamente para lidar com essas propriedades únicas dos dados em grafo.3
Um grafo $G$ é um par ordenado $G = (V, E)$ onde:
Exemplo Concreto 2.1: Considere uma rede social simples com 4 pessoas:
$V = {v_1, v_2, v_3, v_4}$
$E = {(v_1, v_2), (v_2, v_3), (v_3, v_4), (v_4, v_1)}$
Este grafo forma um ciclo — cada pessoa conhece exatamente duas outras.
Grafo Não Direcionado: Se João conhece Maria, Maria conhece João. Conexão bidirecional.
Grafo Direcionado: Se João segue Maria no Twitter, Maria não segue João necessariamente. Conexão unidirecional.
Grafo Ponderado: Cada amizade tem “força” — melhor amigo vs. conhecido.
Grafo Simples: Sem loops (pessoa conectada a si mesma) nem múltiplas conexões entre o mesmo par.
Para um grafo com $N$ vértices, a matriz de adjacência $A$ é $N \times N$:
\[A_{ij} = \begin{cases} 1 & \text{se existe aresta de } i \text{ para } j \\ 0 & \text{caso contrário} \end{cases}\]Exemplo Prático 2.3.1: Usando nosso grafo social:
\[A = \begin{bmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{bmatrix}\]Onde cada linha representa as conexões de um vértices: $v_1$ conecta a $v_2$ e $v_4$, $v_2$ conecta a $v_1$ e $v_3$, e assim por diante.
Nota a simetria — reflexo da natureza não direcionada.
A matriz diagonal $D$ onde $D_{ii}$ = número de conexões do vértices $i$:
\[D_{ii} = \sum_{j=1}^{N} A_{ij}\]Cálculo Manual 2.3.2: Para nosso exemplo:
Imagine uma conversa em uma festa. Cada pessoa (vértices) escuta seus vizinhos imediatos, processa as informações, e forma uma nova opinião. Repita isso várias rodadas — pessoas distantes começam a influenciar umas às outras indiretamente.
Esse é o princípio das GNNs: propagação de mensagens.
Matematicamente:
\[h_i^{(l+1)} = \text{ATUALIZAÇÃO}\left(h_i^{(l)}, \text{AGREGAÇÃO}\left(\{h_j^{(l)} : j \in N(i)\}\right)\right)\]Onde:
A Graph Convolutional Network elegantemente resolve propagação de mensagens usando álgebra linear. Sua fórmula define uma era:
\[H^{(l+1)} = \sigma\left(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}H^{(l)}W^{(l)}\right)\]$H^{(l)}$: Matriz $N \times F_l$ com características de todos os vértices na camada $l$
$W^{(l)}$: Matriz de pesos treináveis $F_l \times F_{l+1}$ — o que a rede aprende
$\sigma(\cdot)$: Função de ativação (ReLU) introduzindo não-linearidade
$\tilde{A} = A + I_N$: Matriz de adjacência com self-loops — cada vértices influencia a si mesmo
$\tilde{D}$: Matriz de grau para $\tilde{A}$
$\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}$: Normalização simétrica prevenindo explossão/desvanecimento de gradientes
Sem self-loops, um vértices “esquece” suas características originais após algumas camadas. A matriz identidade $I_N$ preserva a informação própria de cada vértices.
vértices populares (alto grau) dominariam a agregação sem normalização. Dividir por $\sqrt{d_i d_j}$ equilibra contribuições independente da popularidade.
Vamos calcular uma camada GCN manualmente para cristalizar o entendimento.
Grafo: Mesmo ciclo de 4 vértices
Características iniciais $H^{(0)}$ (2 features por vértices):
Onde cada linha representa: $v_1$ com [energia=1.0, sociabilidade=0.5], $v_2$ com [energia=0.8, sociabilidade=0.2], e assim por diante.
Pesos $W^{(0)}$ (output 2D):
\[W^{(0)} = \begin{bmatrix} 0.5 & 0.3 \\ 0.1 & 0.4 \end{bmatrix}\]Graus em $\tilde{A}$:
Interpretação: Cada vértices agora combina suas características com as de seus vizinhos, ponderadas igualmente.
Como todos os valores são positivos, ReLU não altera nada:
\[H^{(1)} = \begin{bmatrix} 0.427 & 0.347 \\ 0.397 & 0.397 \\ 0.317 & 0.303 \\ 0.360 & 0.363 \end{bmatrix}\]Resultado: Cada vértices possui novas características que codificam tanto informações próprias quanto de sua vizinhança.
GNNs não existem no vácuo. Elas resolvem problemas específicos:
Classificação de vértices: Spam vs. usuário legítimo
softmax$(H^{(L)}W_{\text{class}})$Classificação de Grafos: Molécula tóxica vs. segura
Predição de Arestas: Novas amizades prováveis
score$(h_i, h_j) = h_i^T h_j$Over-smoothing: Muitas camadas → todos os vértices ficam idênticos
Agregação Simplista: Média ponderada pode perder nuances
Grafos Homogêneos: Assume todos os vértices/arestas são iguais
GraphSAGE: Amostragem de vizinhos para grafos grandes
GAT: Mecanismo de atenção para pesos adaptativos
Graph Transformer: Self-attention global entre vértices
A GCN revoluciona como processamos dados relacionais. Sua elegância matemática esconde poder computacional profundo: transformar conexões em conhecimento.
Você dominou:
Próximos passos: Implementar GCNs em PyTorch, explorar GraphSAGE e GATs, aplicar em datasets reais.
A revolução das GNNs começou. Seja parte dela.
Este capítulo estabelece fundação sólida para arquiteturas mais sofisticadas. Cada conceito aqui resurge em variantes avançadas — domine-os agora, colha benefícios depois.
BARABÁSI, Albert-László. Linked: a nova ciência das redes. Tradução de Jonas Pereira dos Santos. São Paulo: Leopardo, 2009. ↩