Começamos com os fundamentos teóricos e seguimos para as aplicações práticas em linguagens de programação funcionais. Explicamos abstração, aplicação e recursão. Mostramos exemplos de currying e combinadores de ponto fixo. O cálculo lambda é a base da computação funcional.

1. Introdução, História e Motivações e Limites

Todos os exercícios desta página foram removidos. Os exercícios estarão disponíveis apenas no livro que está sendo escrito. Removi também o capítulo sobre cálculo lambda simplesmente tipado.

O cálculo lambda é uma teoria formal para expressar computação por meio da visão de funções como fórmulas. Um sistema para manipular funções como sentenças, desenvolvido por Alonzo Church sob uma visão extensionista das funções na década de 1930. Nesta teoria usamos funções para representar todos os dados e operações. Em cálculo lambda, tudo é uma função e uma função simples é parecida com:

Esta função adiciona $1$ ao seu argumento. O $\lambda$ indica que estamos definindo uma função.

Na teoria da computação definida por Church com o cálculo lambda existem três componentes básicos: as variáveis: $x\,$, $y\,$, $z$; as abstrações $\lambda x.\;E\,$. O termo $E$ representa uma expressão lambda e a aplicação $(E\;M)\,$. Com estes três componentes e o cálculo lambda é possível expressar qualquer função computacionalmente possível.

A década de 1930 encerrou a busca pela consistência da matemática iniciada nas última décadas do século XIX. Neste momento histórico os matemáticos buscavam entender os limites da computação. Questionavam: Quais problemas podem ser resolvidos por algoritmos? Existem problemas não computáveis?

Estas questões surgiram como consequência dos trabalhos no campo da lógica e da lógica combinatória que despontaram no final do século XIX e começo do século XX. Em um momento crítico, Church ofereceu respostas, definindo que as funções computáveis são aquelas que podem ser expressas em cálculo lambda. Um exemplo simples de função computável seria:

Esta função soma dois números. Todas as funções lambda são, por definição unárias e anônimas. Assim, a função acima está sacrificando o rigor matemático para facilitar o entendimento. Esta é uma liberdade que é abusada descaradamente, neste livro, sempre com a esperança que estando mais próximo do que aprendemos nos ciclos básicos de estudo, é mais simples criar o nível de entendimento necessário.

O trabalho de Church estabeleceu limites claros para computação, ajudando a revelar o que é e o que não é computável. Sobre esta formalização foi construída a Ciência da Computação. Seu objetivo era entender e formalizar a noção de computabilidade. Church buscava um modelo matemático preciso para computabilidade. Nesta busca ele criou uma forma de representar funções e operações matemáticas de forma abstrata, usando como base a lógica combinatória desenvolvida anos antes ¹.

Na mesma época, Alan Turing propôs a máquina de Turing, uma abordagem diferente para tratar a computabilidade. Apesar das diferenças, essas duas abordagens provaram ser equivalentes e, juntas, estabeleceram os alicerces da teoria da computação moderna. O objetivo de Church era capturar o conceito de cálculo efetivo². Em 1936, no artigo On computable numbers, with an application to the Entscheidungsproblem³, Turing criou a Ciência da Computação e iniciou a computação artificial determinando o futuro da civilização⁴.

O artigo On computable numbers, with an application to the Entscheidungsproblem foi submetido para publicação em 28 de maio de 1936. Sendo esta a data de nascimento da Ciência da Computação.

Seu trabalho foi uma das primeiras tentativas de formalizar matematicamente o ato de computar. Mais tarde, a equivalência entre o cálculo lambda e a máquina de Turing consolidou a ideia de que ambos podiam representar qualquer função computável, levando à formulação da Tese de Church-Turing. Afirmando que qualquer função computável pode ser resolvida pela máquina de touring e, equivalentemente, pelo cálculo lambda, fornecendo uma definição matemática precisa do que é, ou não é, computável.

A partir do meio da década de 1930, vários matemáticos e lógicos, como Church, Turing, Gödel e Post, desenvolveram modelos diferentes para formalizar a computabilidade. Cada um desses modelos abordou o problema de uma perspectiva exclusiva. Como pode ser visto na Tabela 1.

Tabela 1.A. Relação entre as contribuições de Church, Gödel e Post

Church propôs o cálculo lambda para descrever funções de forma simbólica, usando a abstração lambda. Esse modelo representa funções como estruturas de primeira classe formalizando a computabilidade de funções e variáveis.

Em 1936, Alan Turing propôs a máquina de Turing. Essa máquina, conceitual, é formada por uma fita infinita que pode ser lida e manipulada por uma cabeça de leitura/escrita, seguindo um conjunto de regras e se movendo entre estados fixos.

A visão de Turing apresentava uma abordagem mecânica da computação, complementando a perspectiva simbólica de Church e sendo complementada por esta. Church havia provado que algumas funções não são computáveis. O Problema da Parada é um exemplo famoso:

Church mostrou que esta função não pode ser expressa no cálculo lambda e, consequentemente, não pode ser computada. A atenta leitora deve saber que Church e Turing, não trabalharam sozinhos.

Kurt Gödel contribuiu com a ideia de funções recursivas, uma abordagem algébrica que define a computação por meio de funções primitivas e suas combinações. Ele explorou a computabilidade a partir de uma perspectiva aritmética, usando funções que podem ser definidas recursivamente. Essa visão trouxe uma base numérica e algébrica para o conceito de computabilidade.

Em paralelo, Emil Post desenvolveu os sistemas de reescrita, ou Cálculo Sentencial, baseados em regras de substituição de strings. O trabalho de Post foi importante para a teoria das linguagens formais e complementou as outras abordagens, fornecendo uma visão baseada em regras de substituição.

Apesar das diferenças estruturais entre o cálculo lambda, as máquinas de Turing, as funções recursivas e o Cálculo Sentencial de Post, todos esses modelos têm o mesmo poder computacional. Uma função que não for computável em um destes modelos, não o será em todos os outros. Neste ponto estava definida a base para a construção da Ciência da Computação.

1.1. A Inovação de Church: Abstração Funcional

O trabalho de Alonzo Church é estruturado sobre a ideia de abstração funcional. Esta abstração permite tratar funções como estruturas de primeira classe. Neste cenário, as funções podem ser passadas como argumentos, retornadas como resultados e usadas em expressões compostas.

No cálculo lambda, uma função é escrita como $\lambda x.\;E\,$. Aqui, $\lambda$ indica que é uma função, $x$ é a variável ligada, na qual a função é aplicada, e $E$ é o corpo da função. Por exemplo, a função que soma $1$ a um número é escrita como $\lambda x.\;x + 1\,$. Isso possibilita a manipulação direta de funções, sem a necessidade de linguagens ou estruturas rígidas. A Figura 1.1.A apresenta o conceito de funções de primeira classe.

Figura 1.1.A: Diagrama de Abstração e Aplicação usando funções no corpo da função. A função principal é a função de ordem superior, ou de primeira classe

No cálculo lambda, uma função de ordem superior é uma função que aceita outra função como argumento ou retorna uma função como resultado. Isso significa que uma função de ordem superior trata funções como valores, podendo aplicá-las, retorná-las ou combiná-las com outras funções.

Seja $f$ uma função no cálculo lambda. Dizemos que $f$ é uma função de ordem superior se:

1. $f$ aceita uma função como argumento.
2. $f$ retorna uma função como resultado.

No cálculo lambda puro, as funções são anônimas. No entanto, em contextos de programação funcional, é comum nomear funções de ordem superior para facilitar seu uso e identificação em operações complexas. Vamos tomar esta licença poética, importada da programação funcional, de forma livre e temerária em todo este texto. Sempre que agradar ao pobre autor.

Considere a mesma função de adição de ordem superior, agora nomeada como adicionar:

\[\text{adicionar} = \lambda x.\; \lambda y.\; x + y\]

Essa função nomeada pode ser usada como argumento para outras funções de ordem superior, como mapear:

\[\text{mapear} \; (\text{adicionar} \; 2) \; [1, 2, 3]\]

Neste caso, a aplicação resulta em:

\[[3, 4, 5]\]

A abstração funcional induziu a criação do conceito de funções anônimas em linguagens de programação, em especial, e em linguagens formais de forma geral. Linguagens de programação, como Haskell, Lisp, Python e JavaScript, adotam essas funções como parte das ferramentas disponíveis em sua sintaxe. Tais funções são conhecidas como lambda functions ou arrow functions.

Na matemática, a abstração funcional possibilitou a criação de operações de combinação, um conceito da lógica combinatória. Estas operações de combinação são representadas na aplicação de combinadores que, por sua vez, definem como combinar funções. No cálculo lambda, e nas linguagens funcionais, os combinadores, como o combinador Y, facilitam a prova de conceitos matemáticos ou, permitem acrescentar funcionalidades ao cálculo lambda. O combinador $Y\,$, por exemplo, permite o uso de recursão em funções. O combinador $Y\,$, permitiu provar a equivalência entre o Cálculo lambda, a máquina de touring e a recursão de Gödel. Solidificando a noção de computabilidade.

Na notação matemática clássica, as funções são representadas usando símbolos de variáveis e operadores. Por exemplo, uma função quadrática pode ser escrita como:

Essa notação é direta e representa um relação matemática entre dois conjuntos. Descrevendo o resultado da aplicação da relação a um dos elementos de un conjunto, encontrando o elemento relacionado no outro. No exemplo acima, se aplicarmos $f$ em $2$ teremos $9$ como resultado da aplicação. A definição da função $f$ não apresenta o processo de computação necessário. Nós sabemos como calcular o resultado porque conhecemos a sintaxe da aritmética e a semântica da álgebra.

O cálculo lambda descreve um processo de aplicação e transformação de variáveis. Enquanto a Máquina de Turing descreve a computação de forma mecânica, o cálculo lambda foca na transformação de expressões. Para começarmos a entender o poder do cálculo lambda, podemos trazer a função $F$ um pouco mais perto dos conceitos de Church.

Vamos começar definindo uma expressão $M$ contendo uma variável $x\,$, na forma:

A medida que $x$ varia no domínio dos números naturais podemos obter a função representada na notação matemática padrão por $x \mapsto x^2 + x + 1$ este relação define o conjunto de valores que $M$ pode apresentar em relação aos valores de $x\,$. Porém, se fornecermos um valor de entrada específico, por exemplo, $2\,$, para $x\,$, valor da função será $2^2 + 4 + 1 = 9\,$.

Avaliando funções desta forma, Church introduziu a notação

Para representar a expressão $M\,$. Nesta representação temos uma abstração. Justamente porque a expressão estática $M(x)\,$, para $x$ fixo, torna-se uma função abstrata representada por $λx:M\,$.

Linguagens de programação modernas, como Python ou JavaScript, têm suas próprias formas de representar funções. Por exemplo, em Python, uma função pode ser representada assim:

-- Define a função f, que toma um argumento x and devolve x^2 + 2*x + 1
f :: Int -> Int
f x = x^2 + 2*x + 1

As linguagens funcionais representam funções em um formato baseado na sintaxe do cálculo lambda. Em linguagens funcionais, funções são tratadas como elementos e a aplicação de funções é a operação que define a computação. Neste ambiente as funções têm tal importância, e destaque, que dizemos que no cálculo lambda, funções são cidadãos de primeira classe. Uma metáfora triste. Porém, consistente.

No cálculo lambda, usamos abstração e aplicação para criar e aplicar funções. Na criação de uma função que soma dois números, escrita como:

A notação $\lambda$ indica que estamos criando uma função anônima. Essa abstração explícita é menos comum na notação matemática clássica na qual, geralmente definimos funções nomeadas.

A atenta leitora deve notar que a abstração e a aplicação são operações distintas do cálculo lambda, como pode ser visto na Figura 1.1.B.

Figura 1.1.B: Diagrama da relação entre abstração e aplicação no cálculo lambda

A abstração, representada por $\lambda x.\;E\,$, define uma função na qual $x$ é o parâmetro e $E$ é o corpo da função. Por exemplo, $\lambda x.\;x + 5$ define uma função que soma $5$ ao argumento fornecido. Outro exemplo é $\lambda f. \lambda x.\;f\;(f\;x)\,$, que descreve uma função que aplica o argumento $f$ duas vezes ao segundo argumento $x\,$.

A abstração cria uma função sem necessariamente avaliá-la. A variável $x$ em $\lambda x.\;E$ está ligada à função e não é avaliada até que um argumento seja aplicado. A abstração é puramente declarativa, descreve o comportamento da função sem produzir um valor imediato.

A aplicação, expressa por $M\;N\,$, é o processo equivalente a avaliar uma função algébrica em um argumento. Aqui, $M$ representa a função e $N$ o argumento que é passado para essa função. Ou, como dizemos em cálculo lambda, o argumento que será aplicado a função*. Considere a expressão:

Neste caso, temos a aplicação da função $\lambda x.\;x + 5$ ao argumento $3\,$, resultando em $8\,$. Outro exemplo:

Neste caso, temos uma função de composição dupla é aplicada à função que multiplica valores por dois e, em seguida, ao número $3\,$, resultando em $12\,$.

Em resumo, a abstração define uma função ao associar um parâmetro a um corpo de expressão; enquanto a aplicação avalia essa função ao fornecer um argumento. Ambas operações são independentes, mas interagem para permitir a avaliação de expressões no cálculo lambda.

O elo entre abstração e aplicação é uma forma de avaliação chamada redução-$beta\,$. Dada uma abstração $λ\,$, $λx:M$ e algum outro termo $N\,$, pensado como um argumento, temos a regra de avaliação, chamada redução-$beta$ dada por:

Neste caso, $M[N/x]$ indica o resultado de substituir $N$ em todas as ocorrências de $x$ em $M\,$. Por exemplo, se $M = λx: (x^2 + x + 1)$ e $N = 2y + 1\,$, teremos:

Esta uma operação puramente formal, inserindo $N$ em todos os lugares em que $x$ ocorra em $M\,$.

Ainda há uma coisa que a amável leitora deve ter em mente antes de continuarmos. No cálculo lambda, os números naturais, as operações aritméticas $+$ e $\times\,$, assim como a exponenciação que usamos em $M$ precisam ser representados como termos $λ\,$. Só assim, a avaliação das expressões lambda irão computar corretamente.

1.2. O Cálculo Lambda e a Lógica

O cálculo lambda possui uma relação direta com a lógica matemática, especialmente através do isomorfismo de Curry-Howard. Esse isomorfismo cria uma correspondência entre provas matemáticas e programas computacionais. Em termos simples, uma prova de um teorema é um programa que constrói um valor a partir de uma entrada, e provar teoremas equivale a computar funções.

Essa correspondência deu origem ao paradigma das provas como programas.

O paradigma de provas como programas é uma correspondência entre demonstrações matemáticas e programas de computador, conhecida como correspondência de Curry-Howard. Segundo esse paradigma, cada prova em lógica formal corresponde a um programa e cada tipo ao qual uma prova pertence corresponde ao tipo de dado que um programa manipula. Essa ideia estabelece uma ponte entre a lógica e a teoria da computação, permitindo a formalização de demonstrações como estruturas computáveis e o desenvolvimento de sistemas de prova automáticos e seguros.

O cálculo lambda define computações e serve como uma linguagem para representar e verificar a correção de algoritmos. Esse conceito se expandiu na pesquisa moderna e fundamenta assistentes de prova e linguagens de programação com sistemas de tipos avançados, como o Sistema F e o Cálculo de Construções.

O Sistema F, conhecido como cálculo lambda polimórfico de segunda ordem, é uma extensão do cálculo lambda que permite quantificação universal sobre tipos. Desenvolvido por Jean-Yves Girard e John Reynolds de forma independente.

O Sistema F é utilizado na teoria da tipagem em linguagens de programação, permitindo expressar abstrações mais poderosas, como tipos genéricos e polimorfismo paramétrico. Servindo como base para a formalização de alguns sistemas de tipos usados em linguagens funcionais modernas.

O Cálculo de Construções é um sistema formal que combina elementos do cálculo lambda e da teoria dos tipos para fornecer uma base para a lógica construtiva. Ele foi desenvolvido por Thierry Coquand e é uma extensão do Sistema F, com a capacidade de definir tipos dependentes e níveis mais complexos de abstração. O cálculo de construções é a base da linguagem Coq, um assistente de prova utilizado para formalizar demonstrações matemáticas e desenvolver software verificado.

A atenta leitora deve ter percebido que o cálculo lambda não é um conceito teórico abstrato; ele possui implicações práticas, especialmente na programação funcional. Linguagens como Lisp, Haskell, OCaml e F# incorporam princípios do cálculo lambda. Exemplos incluem:

1. Funções como cidadãos de primeira classe: No cálculo lambda, funções são valores. Podem ser passadas como argumentos, retornadas como resultados e manipuladas livremente. Isso é um princípio central da programação funcional, notadamente em Haskell.

2. Funções de ordem superior: O cálculo lambda permite a criação de funções que operam sobre outras funções. Isso se traduz em conceitos aplicados em funções como map, filter e reduce em linguagens funcionais.

3. currying: A técnica de transformar uma função com múltiplos argumentos em uma sequência de funções de um único argumento é natural no cálculo lambda e no Haskell e em outras linguagens funcionais.

4. Avaliação preguiçosa (lazy): Embora não faça parte do cálculo lambda puro, a semântica de redução do cálculo lambda, notadamente a estratégia de redução normal inspirou o conceito de avaliação preguiçosa em linguagens como Haskell.

5. Recursão: Definir funções recursivas é essencial em programação funcional. No cálculo lambda, isso é feito com combinadores de ponto fixo.

1.3. Representação de Valores e Computações

Uma das características principais do cálculo lambda é representar valores, dados e computações complexas, usando exclusivamente funções. Até números e booleanos são representados de forma funcional. Um exemplo indispensável é a representação dos números naturais, chamada Numerais de Church:

Voltaremos a esta notação mais tarde. O importante é que essa codificação permite que operações aritméticas sejam definidas inteiramente em termos de funções. Por exemplo, a função sucessor, usada para provar a criação de conjuntos de números contáveis, como os naturais e os inteiros, pode ser expressa como:

Assim, operações como adição e multiplicação podem ser construídas usando termos lambda.

Um dos resultados mais profundos da formalização da computabilidade, utilizando o cálculo lambda e as máquinas de Turing, foi a identificação de problemas indecidíveis. Problemas para os quais não podemos decidir se o algoritmo que os resolve irá parar em algum ponto, ou não.

O exemplo mais emblemático é o Problema da Parada, formulado por Alan Turing em 1936. O Problema da Parada questiona se é possível construir um algoritmo que, dado qualquer programa e uma entrada, determine se o programa eventualmente terminará ou continuará a executar indefinidamente. Em termos formais, essa questão pode ser expressa como:

Turing demonstrou, por meio de um argumento de diagonalização, que tal função $f$ não pode existir. Esse resultado mostra que não é possível determinar, de forma algorítmica, o comportamento de todos os programas para todas as possíveis entradas.

Outro problema indecidível, elucidado pelas descobertas em computabilidade, é o décimo problema de Hilbert. Esse problema questiona se existe um algoritmo que, dado um polinômio com coeficientes inteiros, possa determinar se ele possui soluções inteiras. Formalmente, o problema pode ser expresso assim:

Os problemas de Hilbert são uma lista de 23 problemas matemáticos propostos por David Hilbert em 1900, durante o Congresso Internacional de Matemáticos em Paris. Esses problemas abordam questões em várias áreas da matemática e estimularam muitas descobertas ao longo do século XX. Cada problema visava impulsionar a pesquisa e delinear os desafios mais importantes da matemática da época. Alguns dos problemas foram resolvidos, enquanto outros permanecem abertos ou foram provados como indecidíveis, como o décimo problema de Hilbert, que pergunta se existe um algoritmo capaz de determinar se um polinômio com coeficientes inteiros possui soluções inteiras.

Em 1970, Yuri Matiyasevich, em colaboração com Julia Robinson, Martin Davis e Hilary Putnam, provou que tal algoritmo não existe. Esse resultado teve implicações profundas na teoria dos números e demonstrou a indecidibilidade de um problema central na matemática.

A equivalência entre o cálculo lambda, as máquinas de Turing e as funções recursivas permitiu estabelecer os limites da computação algorítmica. O Problema da Parada e outros resultados indecidíveis, como o décimo problema de Hilbert, mostraram que existem problemas além do alcance dos algoritmos.

A Tese de Church-Turing formalizou essa ideia, afirmando que qualquer função computável pode ser expressa por um dos modelos computacionais mencionados, Máquina de Turing, recursão e o cálculo lambda⁵. Essa tese forneceu a base rigorosa necessária ao desenvolvimento da Ciência da Computação, permitindo a demonstração da existência de problemas não solucionáveis por algoritmos.

1.4. Limitações do Cálculo Lambda e Sistemas Avançados

O cálculo lambda é poderoso. Ele pode expressar qualquer função computável. Mas tem limitações: não tem tipos nativos ou qualquer sistema de tipos. Tudo é função. Números, booleanos, estruturas de dados são codificados como funções; Não tem estado mutável. cada expressão produz um novo resultado. Não modifica valores existentes. Isso é uma vantagem em alguns cenários, mas agrega complexidade à definição de algoritmos; não tem controle de fluxo direto, Loops e condicionais são simulados com funções recursivas.

Apesar de o cálculo lambda ser chamado de a menor linguagem de programação a criação de algoritmos sem controle de fluxo não é natural para programadores, ou matemáticos, nativos do mundo imperativo.

Por fim, o cálculo lambda pode ser ineficiente. Por mais que doa confessar isso. Mas temos que admitir que codificações como números de Church podem levar a cálculos lentos. Performance nunca foi um objetivo.

Sistemas mais avançados de cálculo lambda abordam algumas das deficiências do cálculo lambda expandindo, provando conceitos, criando novos sistemas lógicos, ou criando ferramentas de integração. Entre estes sistemas, a leitora poderia considerar:

1. Sistemas de tipos: o cálculo lambda tipado adiciona tipos. O Sistema F, por exemplo, permite polimorfismo. A função $\Lambda \alpha. \lambda x:\alpha.\;x$ é polimórfica e funciona para qualquer tipo $\alpha\,$.

2. Efeitos colaterais: o cálculo lambda com efeitos colaterais permite mutação e I/O. A função $\text{let}\;x = \text{ref}\;0\;\text{in}\;x := !x + 1$ cria uma referência mutável e providencia um incremento.

3. Construções imperativas: algumas extensões adicionam estruturas de controle diretas. Este é o caso de $\text{if}\;b\;\text{then}\;e_1\;\text{else}\;e_2\,$. Neste caso, temos um condicional direto, não implementado como uma função.

4. Otimizações: implementações eficientes usam representações otimizadas. A função $2 + 3 \rightarrow 5$ usa aritmética tradicional, não números de Church. Aqui, a observadora leitora já deve ter percebido que, neste livro, quando encontrarmos uma operação aritmética, vamos tratá-la como tal.

Estas extensões agregam funcionalidade e transformam o cálculo lambda em uma ferramenta matemática mais flexível. Muitas vezes com o objetivo de criar algoritmos, facilitar o uso de linguagens de programação baseadas em cálculo lambda no universo fora da matemática.

1.5. Notações e Convenções

O cálculo lambda utiliza uma notação específica para representar funções, variáveis, termos e operações. Abaixo estão as notações e convenções, além de algumas expansões necessárias para a compreensão completa.

1.4.1. Símbolos Básicos

• $\lambda$: indica a definição de uma função anônima. Por exemplo, $\lambda x.\;x + 1$ define uma função que recebe $x$ e retorna $x + 1\,$.

• Variáveis: letras minúsculas, como $x\,$, $y\,$, $z\,$, representam variáveis no cálculo lambda.

• Termos: letras maiúsculas, como $M\,$, $N\,$, representam termos ou expressões lambda.

• Aplicação de função: a aplicação de uma função a um argumento é representada como $(M\;N)\,$. Na aplicação $M$ é uma função e $N$ é o argumento. Quando há múltiplas aplicações, como em $((M\;N)\;P)\,$, elas são processadas da esquerda para a direita.

• Redução: a seta $\rightarrow$ indica o processo de avaliação, ou redução, de uma expressão lambda. Por exemplo, $(\lambda x.\;x + 1)\;2 \rightarrow 3\,$. Indica que depois da aplicação e substituição a função chegará a $3\,$.

• redução-$beta$: a notação $ \rightarrow_\beta $ é usada para indicar a redução beta, um passo específico de substituição em uma expressão lambda. Exemplo: $(\lambda x.\;x + 1)\;2 \rightarrow_\beta 3\,$. A redução beta será a substituição de $x$ por $2\,$, resultando em $2+1$ e finalmente em $3\,$.

• Equivalência de termos: o símbolo $\equiv$ denota equivalência entre termos. Dois termos $M \equiv N$ são considerados estruturalmente equivalentes.

1.4.2. Tipagem e Contexto

• Contexto de Tipagem ($\Gamma$): representa o contexto de tipagem, que é um conjunto de associações entre variáveis e seus tipos. Por exemplo, $\Gamma = { x: \text{Nat}, y: \text{Bool} }\,$. Dentro de um contexto $\Gamma\,$, um termo pode ter um tipo associado: $\Gamma \vdash M : A$ significa que no contexto $\Gamma\,$, o termo $M$ tem tipo $A\, \,$.

• Julgamento de tipo: o símbolo $\vdash$ é utilizado para julgar o tipo de um termo dentro de um contexto de tipagem. Por exemplo, $\Gamma \vdash M : A$ significa que, no contexto $\Gamma\,$, o termo $M$ tem o tipo $A\,$.

• Tipagem explícita: usamos $x : A$ para declarar que a variável $x$ tem tipo $A\,$. Por exemplo, $n : \text{Nat}$ indica que $n$ é do tipo número natural ($\text{Nat}$).

1.4.3. Funções de Alta Ordem e Abstrações

• Funções de Alta Ordem: funções que recebem outras funções como argumentos ou retornam funções como resultado são chamadas de funções de alta ordem. Por exemplo, $(\lambda f. \lambda x.\;f(f\;x))$ é uma função de alta ordem que aplica $f$ duas vezes ao argumento $x\,$.

• Abstrações Múltiplas: abstrações aninhadas podem ser usadas para criar expressões mais complexas, como $(\lambda x.\;(\lambda y.\;x + y))\,$. Esse termo define uma função que retorna outra função.

1.4.4. Variáveis Livres e Ligadas

• Variáveis Livres: uma variável $x$ é considerada livre em uma expressão lambda se não estiver ligada a um operador $\lambda\,$. A notação $FV(M)$ é usada para representar o conjunto de variáveis livres, Free Variables, em um termo $M\,$. Por exemplo, em $\lambda y.\;x + y\,$, a variável $x$ é livre e $y$ é ligada.

• Variáveis Ligadas: uma variável é considerada ligada se estiver associada a um operador $\lambda\,$. Por exemplo, em $\lambda x.\;x + 1\,$, a variável $x$ é ligada. A notação $BV(M)$ representa o conjunto das variáveis ligadas, Bound Variable, no termo $M\,$.

1.4.5. Operações Aritméticas

O cálculo lambda permite incluir operações aritméticas dentro das expressões. Por exemplo:

• Adição: $x + 1\,$, neste caso, $x$ é uma variável e $+$ é a operação de soma.
• Multiplicação: $x \times 2\,$, na qual, $\times$ representa a multiplicação.
• Potência: $x^2\,$, o operador de potência eleva $x$ ao quadrado.
• Operações compostas: exemplos incluem $x^2 + 2x + 1$ e $x \times y\,$, que seguem as regras usuais de aritmética.

1.4.6. Expansões Específicas

• Notação de Tuplas e Produtos Cartesianos: o produto cartesiano de conjuntos pode ser representado por notações como $(A \times B) \rightarrow C\,$, que denota uma função que recebe um par de elementos de $A$ e $B$ e retorna um valor em $C\,$.

• Funções Recursivas: funções recursivas podem ser descritas usando notação lambda. Um exemplo comum é a definição da função de fatoriais: $f = \lambda n.\;\text{if}\;n = 0\;\text{then}\;1\;\text{else}\;n \times f(n - 1)\,$.

1.4.7. Notações Alternativas

• Parênteses Explícitos: frequentemente os parênteses são omitidos por convenção, mas podem ser adicionados para clareza em expressões mais complexas, como $((M\;N)\;P)\,$.

• Reduções Sequenciais: Quando múltiplas reduções são realizadas, pode-se usar notação como $M \rightarrow_\beta N \rightarrow_\beta P\,$, para descrever o processo completo de avaliação.

1.4.8. Convenção de Nomes e Variáveis Livres e Ligadas

No cálculo lambda, as variáveis têm escopo léxico. O escopo é determinado pela estrutura sintática do termo, não pela ordem de avaliação. Uma variável é ligada quando aparece dentro do escopo de uma abstração que a introduz. Por exemplo: em $\lambda x.\lambda y.x\;y\,$, tanto $x$ quanto $y$ estão ligadas e em $\lambda x.(\lambda x.\;x)\;x\,$, ambas as ocorrências de $x$ estão ligadas, mas a ocorrência interna (no termo $\lambda x.\;x$) sombreia a externa.

Uma variável é livre quando não está ligada por nenhuma abstração. por exemplo: em $\lambda x.\;x\;y\,$, $x$ está ligada, mas $y$ está livre. Ou ainda, em $(\lambda x.\;x)\;y\,$, $y$ está livre.

O conjunto de variáveis livres de um termo $E\,$, denotado por $FV(E)\,$, pode ser definido recursivamente:

1. $FV(x) = {x}$
2. $FV(\lambda x.\;E) = FV(E) \setminus {x}$
3. $FV(E\;N) = FV(E) \cup FV(N)$

Formalmente dizemos que para qualquer termo termo lambda $M\,$, o conjunto $FV(M)$ de variáveis livres de $M$ e o conjunto $BV(M)$ de variáveis ligadas em $M$ são definidos de forma indutiva da seguinte:

1. Se $M = x$ (uma variável), então:
   • $FV(x) = {x}$
   • $BV(x) = \emptyset$
2. Se $M = (M_1 M_2)\,$, então:
   • $FV(M) = FV(M_1) \cup FV(M_2)$
   • $BV(M) = BV(M_1) \cup BV(M_2)$
3. Se $M = (\lambda x: M_1)\,$, então:
   • $FV(M) = FV(M_1) \setminus {x}$
   • $BV(M) = BV(M_1) \cup {x}$

Se $x \in FV(M_1)\,$, dizemos que as ocorrências da variável $x$ ocorrem no escopo de $\lambda\,$. Um termo lambda $M$ é fechado se $FV(M) = \emptyset\,$, ou seja, se não possui variáveis livres.

O que a atenta leitora não deve perder de vista é que as variáveis ligadas são somente marcadores de posição, de modo que elas podem ser renomeadas livremente sem alterar o comportamento de redução do termo, desde que não entrem em conflito com as variáveis livres.

Os termos $\lambda x:\;(x(\lambda y:\;x(y\;x))$ e $\lambda x:\;(x(\lambda z: x\;(z\;x))$ devem ser considerados equivalentes. Da mesma forma, os termos $\lambda x:\; (x\;(\lambda y:\; x\;(y\;x))$ e $\lambda w:\; (w\;(\lambda z:\; w\;(z\;w))$ serão considerados equivalentes. No cálculo lambda está definido um conjunto de regras, redução-$\alpha$ que determina como podemos renomear variáveis.

Exemplo:

e

A amável leitora deve entender o conceito de variáveis livres e ligadas observando uma convenção importante no cálculo lambda que diz que podemos renomear variáveis ligadas, Bound Variables, sem alterar o significado do termo, desde que não capturemos variáveis livres, Free Variables, durante o processo de renomeação. Esta operação é chamada de redução-$\alpha$ e é estudada com mais fervor em outra parte do livro. Neste momento, podemos dizer que essa renomeação não deve alterar o comportamento ou o significado da função, desde que seja feita com cuidado evitando a captura de variáveis livres. A afoita leitora pode avaliar os exemplos a seguir:

Exemplo 1: renomeação segura de variáveis ligadas. Considere a expressão:

Nesta expressão, temos duas abstrações aninhadas. A primeira, $\lambda x\,$, define uma função que recebe $x$ como argumento. A segunda, $\lambda y\,$, define uma função que recebe $y\,$. O termo $x\;y$ é a aplicação de $x$ ao argumento $y\,$. Este termo pode ser visto na árvore sintática a seguir:

A observadora leitora já deve ter percebido que podemos realizar uma redução-$\alpha$ para renomear as variáveis ligadas sem alterar o significado da expressão. Como não há variáveis livres aqui, podemos renomear $x$ para $z$ e $y$ para $w$:

As variáveis ligadas $x$ e $y$ foram renomeadas para $z$ e $w\,$, respectivamente, mas o significado da função permanece o mesmo: ela ainda aplica o primeiro argumento ao segundo. Este é um exemplo de renomeação correta, sem captura de variáveis livres.

Exemplo 2: problema de captura de variáveis livres. Para entender este problema, vejamos o segundo exemplo:

No primeiro termo, $y$ é uma variável livre, ou seja, não está ligada por uma abstração $\lambda$ dentro da expressão e pode representar um valor externo. Se tentarmos renomear $x$ para $y\,$, acabamos capturando a variável livre $y$ em uma abstração. No segundo termo, $y$ se torna uma variável ligada dentro da abstração $\lambda y\,$, o que altera o comportamento do termo. O termo original dependia de $y$ como uma variável livre, mas no segundo termo, $y$ está ligada e aplicada a si mesma:

No termo original, $y$ poderia ter um valor externo fornecido de outro contexto. No termo renomeado, $y$ foi capturada e usada como uma variável ligada, o que altera o comportamento do termo. Este é um exemplo de renomeação incorreta por captura de uma variável livre, mudando o significado do termo original.

2. Sintaxe e Semântica

O cálculo lambda usa uma notação simples para definir e aplicar funções. Ele se baseia em três elementos principais: variáveis, abstrações e aplicações.

As variáveis representam valores que podem ser usados em expressões. Uma variável é um símbolo que pode ser substituído por um valor ou outra expressão. Por exemplo, $x$ é uma variável que pode representar qualquer valor.

A abstração é a definição de uma função. No cálculo lambda, uma abstração é escrita usando a notação $\lambda\,$, seguida de uma variável, um ponto e uma expressão. Por exemplo:

Aqui, $\lambda x.$ indica que estamos criando uma função de $x$. A expressão $x^2 + 2x + 1$ é o corpo da função. A abstração define uma função anônima que pode ser aplicada a um argumento.

A aplicação é o processo de usar uma função em um argumento. No cálculo lambda, representamos a aplicação de uma função a um argumento colocando-os lado a lado. Por exemplo, se tivermos a função $\lambda x.\;x + 1\;$ e quisermos aplicá-la ao valor $2\,$, escrevemos:

O resultado da aplicação é a substituição da variável $x$ pelo valor $2\,$, resultando em $2 + 1$ equivalente a $3\,$. Outros exemplos interessantes de função são a função identidade, que retorna o próprio valor e que é escrita como $\lambda x.\;x$ e uma função que some dois números e que pode ser escrita como $\lambda x. \lambda y.\;(x + y)\,$.

No caso da função que soma dois números, $\lambda x. \lambda y.\;(x + y)\,$, temos duas abstrações $\lambda x$ e $\lambda y\,$, cada uma com sua própria variável. Logo, $\lambda x. \lambda y.\;(x + y)$ precisa ser aplicada a dois argumentos. Tal como: $\lambda x. \lambda y.\;(x + y)\;3\;4\,$.

Formalmente dizemos que:

1. Se $x$ é uma variável, então $x$ é um termo lambda.

2. Se $M$ e $N$ são termos lambda, então $(M\; N)$ é um termo lambda chamado de aplicação.

3. Se $E$ é um termo lambda, e $x$ é uma variável, então a expressão $(λx. E)$ é um termo lambda chamado de abstração lambda.

Esses elementos básicos, variáveis, abstração e aplicação, formam a base do cálculo lambda. Eles permitem definir e aplicar funções de forma simples sem a necessidade de nomes ou símbolos adicionais.

2.1. Estrutura Sintática - Gramática

O cálculo lambda é um sistema formal para representar computação baseado na abstração de funções e sua aplicação. Sua sintaxe é simples, porém expressiva. Enfatizando a simplicidade. Tudo é uma expressão, ou termo, e existem três tipos de termos:

1. Variáveis: representadas por letras minúsculas como $x\,$, $y\,$, $z\,$. As variáveis não possuem valor intrínseco, como acontece nas linguagens imperativa. Variáveis atuam como espaços reservados para entradas potenciais de funções.

2. Aplicação: a aplicação $(M\;N)$ indica a aplicação da função $M$ ao argumento $N\,$. A aplicação é associativa à esquerda, então $M\;N\;P$ é interpretado como $((M\;N)\;P)\,$.

3. Abstração: a abstração $(\lambda x.\;E)$ representa uma função que tem $x$ como parâmetro e $E$ como corpo. O símbolo $\lambda$ indica que estamos definindo uma função. Por exemplo, $(\lambda x.\;x)$ é a função identidade.

A abstração é a base do cálculo lambda. Ela permite criar funções anonimas. Um conceito importante relacionado à abstração é a distinção entre variáveis livres e ligadas. Uma variável é ligada se aparece no escopo de uma abstração lambda que a define. Em $(\lambda x.\;x\;y)\,$, $x$ é uma variável ligada. Por outro lado, uma variável é livre se não estiver ligada a nenhuma abstração. No exemplo anterior, $y$ é uma variável livre.

A distinção entre variáveis livres e ligadas permitirá o entendimento da operação de substituição no cálculo lambda. A substituição é a base do processo de computação no cálculo lambda. O poder computacional do cálculo lambda está na forma como esses elementos simples podem ser combinados para expressar operações complexas como valores booleanos, estruturas de dados e até mesmo recursão usando esses os conceitos básicos, variáveis, abstração e aplicação, e a existência, ou não, de variáveis ligadas. Formalmente, podemos definir a sintaxe do cálculo lambda usando uma gramática representada usando sintaxe da Forma de Backus-Naur (BNF):

A gentil leitora pode facilitar o entendimento de abstrações e aplicações se pensar em um termo lambda como sendo uma árvore, cuja forma corresponde à forma como o termo aplica as regras de produção da gramática. Chamamos a árvore criada pela derivação das regras de produção de de árvore sintática ou árvore de derivação. Para um dado termo $M\,$, qualquer, está árvore terá vértices rotulados por $\lambda x$ ou $@\,$, enquanto as folhas serão rotuladas por variáveis.

Indutivamente, podemos definir que a árvore de construção de uma variável $x$ é somente uma folha, rotulada por $x\,$. A árvore de construção de uma abstração $\lambda x.\;E$ consistirá em um vértice rotulado por $\lambda x$ com uma única subárvore, que é a árvore de construção de $E\,$. Por fim, a árvore de construção de uma aplicação $E\;N$ consistirá em um vértice rotulado por $@$ com duas subárvores: a subárvore esquerda é a árvore de construção de $E$ e a subárvore direita é a árvore de construção de $N\,$. Por exemplo, a árvore de construção do termo $\lambda x \lambda y.\;x\;y\;\lambda z.\;y\;z$ será:

Neste texto, vamos dar prioridade a derivação gramatical, deixando as árvores para suporte a explicação das abstrações. Pelo sim, pelo não, vamos ver mais dois exemplos.

Exemplo 1: Representação da abstração $\lambda x.\;x\;x$

Antes de vermos a árvore, podemos analisar a estrutura do termo $\lambda x.\;x\;x\,$. Nesta expressão, o termo $\lambda x$ indica que $x$ é o parâmetro da função e o corpo da função é $x\;x\,$, a aplicação de $x$ a si mesmo.

Agora que a curiosa leitora entendeu a expressão construir a árvore.

Esta árvore é composta de um vértice raiz, no topo, $\lambda x\,$, indicando a abstração de $x\,$. Logo em seguida, a leitora pode ver o vértice de aplicação $@$ no meio da árvore representando que $x$ está sendo aplicado a $x\,$. Finalmente, as folhas da árvore são as variáveis $x$ à esquerda e à direita do vértice de aplicação, correspondendo às duas ocorrências de $x$ no corpo da função.

Exemplo 2: Representação da aplicação $(\lambda x.\;x + 1)\;2$

Outra vez podemos começar com a estrutura do termo $(\lambda x.\;x + 1)\;2\,$. A expressão $\lambda x.\;x + 1$ define uma função que recebe $x$ como argumento e retorna $x + 1\,$. O termo $2$ é o argumento que é passado para a função. Consequentemente, a aplicação $(\lambda x.\;x + 1)\;2$ envolve a substituição de $x$ por $2$ no corpo da função, o que resultará na expressão $2 + 1\,$. Esta função é representada pela árvore:

A árvore sintática representa a aplicação de uma função a um argumento. O vértice de aplicação é representado por $@$ e suas subárvores mostram a função e o argumento.

Em detalhes, temos: o vértice de aplicação, $@\,$, no topo da árvore indica uma aplicação. Não poderia ser diferente já que a aplicação de uma função a um argumento é sempre representada por esse vértice. O galho à esquerda, e abaixo do vértice de aplicação, representa $\lambda x.\;x + 1\,$. Essa parte da árvore representa a função que toma $x$ como parâmetro e retorna $x + 1\,$. Abaixo de $\lambda x\,$, está o corpo da função, $x + 1\,$, que mostra como o argumento $x$ é manipulado. No galho a direita do vértice de aplicação está o valor $2\,$. Este é o argumento que é aplicado a função. Ou, sendo mais claro, o valor $2$ substituirá $x$ no corpo da função. Por último, temos o corpo da função no nível mais baixo, sob $\lambda x\,$, vemos o corpo da função $x + 1\,$. No processo de redução, esse termo é avaliado como $2 + 1\,$, resultando em $3\,$.

Como vimos, a gramática é simples, poucas regras de produção e poucos símbolos. Entretanto, a combinação destas regras pode criar termos complexos. Para facilitar o entendimento a semântica do cálculo lambda pode ser dividida em semântica operacional e semântica denotacional. A semântica denotacional especifica o significado dos termos da linguagem enquanto a semântica operacional especifica o que acontece quado estes termos são executados. A esperta leitora deve estar pensando que a semântica operacional é mais direta já que, podemo relacionar a semântica operacional com a forma como as expressões, ou uma linguagem formal deve funcionar.

2.2. Semântica Operacional

A semântica operacional é uma abordagem rigorosa para descrever o comportamento de linguagens formai, especificando como as expressões de uma linguagem são avaliadas. No caso de linguagens de programação é a semântica operacional que define como os programas irão funcionar.

No contexto do cálculo lambda, a semântica operacional se concentra em como os termos são transformados por meio de uma sequência de reduções. As reduções operam sobre a estrutura sintática dos termos, permitindo a análise detalhada do processo de avaliação, desde a aplicação de funções até a substituição de variáveis.

Abaixo, são apresentadas as principais reduções operacionais utilizadas no cálculo lambda:

1. Redução Beta: A regra que define a ação de aplicação e chamada de redução beta ou redução-$beta$. Usamos a redução beta quando uma função é aplicada a um argumento. Neste caso, a redução beta substitui a variável ligada no corpo da função pelo argumento fornecido:

   \[(\lambda x.\;e_1)\;e_2\;\rightarrow\;e_1[x := e_2]\]

   Isso significa que aplicamos a função $\lambda x.\;e_1$ ao argumento $e_2\,$, substituindo $x$ por $e_2$ em $e_1\,$.

   Exemplo: considere o termo:

   \[(\lambda x.\;x^2)\;3\;\rightarrow\;3^2\]

   Existem duas estratégias para realização da redução beta:

   1. Ordem normal: reduzimos a aplicação mais à esquerda e mais externa primeiro. Essa estratégia sempre encontra a forma normal, se esta existir.

      Exemplo: considere o termo:

      \[(\lambda x.\;(\lambda y.\;y + x)\;2)\;(3 + 4)\]

      Não reduzimos $3 + 4$ imediatamente. Aplicamos a função externa:

      \[(\lambda x.\;(\lambda y.\;y + x)\;2)\;7\]

      Substituímos $x$ por $(3 + 4)$ em $(\lambda y.\;y + x)\;2$:

      \[(\lambda y.\;y + (3 + 4))\;2\]

      Aplicamos a função interna:

      \[2 + (3 + 4) \rightarrow 9\]

   2. Ordem aplicativa: avaliamos primeiro os subtermos (argumentos) antes de aplicar a função.

      Exemplo:

      \[(\lambda x.\;(\lambda y.\;y + x)\;2)\;(3 + 4)\]

      Avaliamos $3 + 4$:

      \[(\lambda x.\;(\lambda y.\;y + x)\;2)\;7\]

      Substituímos $x$ por $7$:

      \[(\lambda y.\;y + 7)\;2\]

      Avaliamos $2 + 7$:

      \[9\]

2. Redução alfa ou redução-$\alpha$: esta redução determina as regras que permitem renomear variáveis ligadas na esperança de evitar conflitos.

   Exemplo:

   \[\lambda x.\;x + 1 \rightarrow \lambda y.\;y + 1\]

3. Redução eta ou redução-$\eta$: esta redução define as regras de captura a equivalência entre funções que produzem os mesmos resultados.

   Exemplo:

   \[\lambda x.\;f(x) \rightarrow f\]

Essas regras garantem que a avaliação seja consistente. Por fim, mas não menos importante, o Teorema de Church-Rosser parece implicar que, se uma expressão pode ser reduzida de várias formas então todas chegarão à mesma forma normal, se esta forma existir⁶.

No cálculo lambda, podemos dizer que um termo está em forma normal quando não é possível realizar mais nenhuma redução beta sobre ele. Ou seja, é um termo que não contém nenhum redex, expressão redutível e, portanto, não pode ser simplificado ou reescrito de nenhuma outra forma. Formalmente: um termo $M$ está em forma normal se:

\[\forall N \, : \, M \not\rightarrow N\]

Isso significa que não existe nenhum termo $N$ tal que o termo $M$ possa ser reduzido a $N\,$.

No cálculo lambda, um termo pode não ter uma forma normal se o processo de redução continuar indefinidamente sem nunca alcançar um termo irredutível. Isso acontece devido à possibilidade de loops infinitos ou recursões que não terminam. Os termos com esta característica são conhecidos como termos divergentes**.

2.3. Substituição

A substituição é a operação estrutural do cálculo lambda. Ela funciona substituindo uma variável livre por um termo, e sua formalização evita a captura de variáveis, garantindo que ocorra de forma correta. A substituição é definida recursivamente:

1. $[N/x] x\;N$
2. $[N/x] y\;y, \quad \text{se}\;x \neq y$
3. $[N/x]\;(M_1 \, M_2) ([N/x]M_1)([N/x]M_2)$
4. $[N/x]\;(\lambda Y \, M) \lambda Y \, ([N/x]M), \quad \text{se} ; x \neq Y \quad \text{e} \quad Y \notin FV(N)$

Aqui, $FV(N)$ é o conjunto de variáveis livres, Free Variable de $N\,$. A condição $y \notin FV(N)$ é necessária para evitar a captura de variáveis livres.

Formalmente dizemos que: para qualquer termo lambda $M$, o conjunto $FV(M)$ de variáveis livres de $M$ e o conjunto $BV(M)$ de variáveis ligadas em $M$ serão definidos de forma indutiva:

1. Se $M = x$ (uma variável), então:
   • $FV(x) = {x}$
   • $BV(x) = \emptyset$
2. Se $M = (M_1 M_2)$, então:
   • $FV(M) = FV(M_1) \cup FV(M_2)$
   • $BV(M) = BV(M_1) \cup BV(M_2)$
3. Se $M = (\lambda x: M_1)$, então:
   • $FV(M) = FV(M_1) \setminus {x}$
   • $BV(M) = BV(M_1) \cup {x}$

Se $x \in FV(M_1)$, dizemos que as ocorrências da variável $x$ ocorrem no escopo de $\lambda$. Um termo lambda $M$ é fechado se $FV(M) = \emptyset$, ou seja, se não possui variáveis livres.

A atenta leitora não deve perder de vista que as variáveis ligadas são unicamente marcadores de posição, de modo que elas podem ser renomeadas livremente sem alterar o comportamento deste termo durante a substituição, desde que não entrem em conflito com as variáveis livres. Por exemplo, os termos $\lambda x:\;(x(\lambda y:\;x(y\;x))$ e $\lambda x:\;(x(\lambda z: x\;(z\;x))$ devem ser considerados equivalentes. Da mesma forma, os termos $\lambda x:\; (x\;(\lambda y:\; x\;(y\;x))$ e $\lambda w:\; (w\;(\lambda z:\; w\;(z\;w))$ devem ser considerados equivalentes.

Exemplo:

e

Podemos pensar na substituição como um processo de buscar e substituir em uma expressão, mas com algumas regras especiais. Lendo estas regras em bom português teríamos:

• A regra 1 (Regra de Substituição Direta): $[N/x]\,x = N$ indica que a variável $x$ será substituída pelo termo $N\,$. Esta é a regra fundamenta a substituição. De forma mais intuitiva podemos dizer que esta regra significa que se encontrarmos exatamente a variável que estamos procurando, substituímos por nosso novo termo. Por exemplo, em $[3/x]\,x\,$, substituímos $x$ por $3\,$.

• A regra 2 (Regra de Variável Livre): $[N/x]\,y = y\,$, se $x \neq y\,$, está correta ao indicar que as variáveis que não são $x$ permanecem inalteradas. Ou seja, se durante a substituição de uma variável encontramos uma variável diferente, deixamos como está. Por exemplo: na substituição $[3/x]\,y\,$, $y$ permanece $y$

• A regra 3 (Regra de Distribuição da Substituição): $[N/x]\;(M_1\;M_2)\,=\,([N/x]M_1)([N/x]M_2)$ define corretamente a substituição em uma aplicação de termos. O que quer dizer que, se estivermos substituindo em uma aplicação de função, fazemos a substituição em ambas as partes. Por exemplo: em $[3/x]\;(x\;y)\,$, substituímos em $x$ e $y$ separadamente, resultando em $(3\;y)\,$.

• A regra 4 (Regra de Evitação de Captura de Variáveis): $[N/x]\;(\lambda y.\;M) \, = \lambda y.\;([N/x]M)\,$, se $x \neq y$ e $y \notin FV(N)\,$, está bem formulada, indicando que a variável vinculada $y$ não será substituída se $x \neq y$ e $y$ não estiverem no conjunto de variáveis livres de $N\,$, o que evita a captura de variáveis. Em uma forma mais intuitiva podemos dizer que se encontrarmos uma abstração lambda, temos que ter cuidado: se a variável ligada for a mesma que estamos substituindo, paramos; se for diferente, substituímos no corpo, mas só se for seguro (sem captura de variáveis). Por exemplo: em $[3/x]\;(\lambda y.\;x)\,$, substituímos $x$ no corpo, resultando em $\lambda y.\;3\,$.

Para que a esforçada leitora possa fixar o entendimento destes conceitos, considere o seguinte exemplo:

Se realizarmos a substituição diretamente, a variável livre $y$ será capturada, alterando o significado do termo original. Para evitar isso, utilizamos a substituição com evasão de captura. Isto é feito com a aplicando a redução-$\alpha$ para as variáveis ligadas que possam causar conflito. Considere:

Neste processo, a variável ligada $y$ foi renomeada como $z$ antes de realizar a substituição, evitando assim a captura da variável livre $y\,$.

Outro exemplo ilustrativo:

Se fizermos a substituição diretamente, a variável $z$ livre em $x$ será capturada pela abstração $\lambda z\,$, modificando o significado do termo. A solução correta é renomear a variável ligada antes da substituição:

Este procedimento assegura que a variável livre $z$ em $x$ não seja capturada pela abstração $\lambda z\,$, preservando o significado original do termo.

Exemplo 1: Substituição direta sem captura de variável livre

Neste caso, substituímos a variável $x$ pelo termo $a$ na expressão $x + y\,$, resultando em $a + y\,$. Não há risco de captura de variáveis livres, pois $y$ não está ligada a nenhuma abstração e permanece livre na expressão resultante.

Exemplo 2: Substituição direta mantendo variáveis livres

Aqui, substituímos $x$ por $b$ na expressão $x\;z\,$, obtendo $b\;z\,$. A variável $z$ permanece livre e não ocorre captura, pois não está sob o escopo de nenhuma abstração lambda que a ligue.

Exemplo 3: Evasão de captura com renomeação de variável ligada

Neste exemplo, se realizássemos a substituição diretamente, a variável livre $y$ em $x$ seria capturada pela abstração $\lambda y\,$, alterando o significado da expressão. Para evitar isso, seguimos os passos:

1. Renomeação (Redução Alfa): Renomeamos a variável ligada $y$ para $z$ na abstração, obtendo $\lambda z.\, [z/y]x\,$.

2. Substituição: Aplicamos $[y/x]\;(x)\,$, resultando em $y\,$.

3. Resultado: A expressão torna-se $\lambda z.\;y \,$, e $y$ permanece livre.

Evitamos a captura da variável livre $y$ pela abstração lambda.

Exemplo 4: Evasão de captura para preservar o significado da expressão

Neste caso, a substituição direta capturaria a variável livre $w$ em $x\,$. Para prevenir isso:

1. Renomeação (Redução Alfa): Renomeamos a variável ligada $w$ para $v\,$, obtendo $\lambda v.\;[v/w]x\,$.

2. Substituição: Aplicamos $[w/x]\;(x)\,$, resultando em $w\,$.

3. Resultado: A expressão fica $\lambda v.\;w\,$, mantendo $w$ como variável livre.

Assim, garantimos que a variável livre $w$ não seja capturada, preservando o significado original da expressão.

Ao aplicar a evasão de captura por meio da renomeação de variáveis ligadas (redução-$\alpha$), asseguramos que as substituições não alterem o comportamento semântico das expressões, mantendo as variáveis livres intactas.

2.3.1. Relação da Substituição com Outros Conceitos do Cálculo Lambda

A substituição não é um processo autônomo. Esta integrada às reduções $\alpha$ e $\beta\,$, ao conceito de variáveis ligadas, ao conceito de recursão e ponto fixo. A atenta leitora já deve ter percebido que sem esta integração a substituição não seria possível, ou não possibilitaria as reduções.

Começando com a redução-$beta$: a redução $beta$ utiliza a substituição como parte de seu mecanismo. A regra de redução beta é definida como:

Neste caso, $[N/x]M$ indica a substituição de todas as ocorrências livres de $x$ em $M$ por $N\,$. Por exemplo:

A computação, ou avaliação de expressões, envolve uma série de reduções beta, cada uma requerendo substituições. Considere a expressão:

Sua avaliação procede assim:

A redução-$\alpha\,$, por outro lado, é usada durante a substituição para evitar a captura de variáveis. Por exemplo:

Neste caso, a redução-$\alpha$ é usada para renomear $y$ para $z$ antes da substituição.

Finalmente, a substituição $[N/x]M\,$, regra primordial da substituição, afeta exclusivamente as ocorrências livres de $x$ em $M\,$. As ocorrências ligadas de $x$ em $M$ permanecem inalteradas. Esta é a relação entre a substituição e os conceitos de variáveis livres e ligadas.

Além destes conceitos que já vimos, a amável leitora, deve ter em mente que a substituição está relacionada com os conceitos de recursão e ponto fixo, que ainda não estudamos neste livro. De fato, a substituição é usada na definição de combinadores de ponto fixo, como o combinador Y:

A aplicação deste combinador envolve substituições que permitem a definição de funções recursivas.

A substituição interage com estes conceitos no funcionamento do cálculo lambda e em sua aplicação em linguagens de programação funcionais. A atenta leitora deve dedicar algum tempo para analisar o código em Haskell, a seguir.

A implementação da substituição em Haskell pode ajudar a concretizar os conceitos teóricos do cálculo lambda. Vamos analisar o código sugerido:

data Expr = Var String | App Expr Expr | Lam String Expr
  deriving (Eq, Show)

-- Função de substituição que inclui a redução alfa para evitar captura
substitute :: String -> Expr -> Expr -> Expr
substitute x n (Var y)
  | x == Y    = n
  | otherwise = Var y
substitute x n (App e1 e2) \, = App (substitute x n e1) (substitute x n e2)
substitute x n (Lam Y e)
  | Y == x = Lam Y e  -- Variável ligada é a mesma que estamos substituindo
  | Y `elem` freeVars n =  -- Risco de captura, aplicar redução alfa
      let y' = freshVar Y (n : e : [])
          e' = substitute Y (Var y') e
      in Lam y' (substitute x n e')
  | otherwise = Lam Y (substitute x n e)

-- Função para obter as variáveis livres em uma expressão
freeVars :: Expr -> [String]
freeVars (Var x) = [x]
freeVars (App e1 e2) = freeVars e1 ++ freeVars e2
freeVars (Lam x e) = filter (/= x) (freeVars e)

-- Função para gerar um novo nome de variável que não cause conflitos
freshVar :: String -> [Expr] -> String
freshVar x exprs = head $ filter (`notElem` allVars) candidates
  where
    allVars = concatMap (\e -> freeVars e ++ boundVars e) exprs
    candidates = [x ++ show n | n <- [1..]]

-- Função para obter as variáveis ligadas em uma expressão
boundVars :: Expr -> [String]
boundVars (Var _) \, = []
boundVars (App e1 e2) \, = boundVars e1 ++ boundVars e2
boundVars (Lam x e) \, = x : boundVars e

Este código possui algumas características que requerem a nossa atenção. Começando com a definição de tipos:

data Expr = Var String | App Expr Expr | Lam String Expr
  deriving (Eq, Show)

Esta linha define, em Haskell, o tipo de dados Expr que representa expressões do cálculo lambda: Var String: representa uma variável; App Expr Expr: representa a aplicação de uma função e Lam String Expr: representa uma abstração lambda.

A seguir, no código, temos a assinatura e a definição da função de substituição que inclui a redução-$\alpha$:

substitute :: String -> Expr -> Expr -> Expr

A função substitute implementa a substituição $[N/x]M\,$. Ela recebe três argumentos: a variável a ser substituída (x); o termo substituto (n) e a expressão na qual fazer a substituição (Expr).

Agora, que definimos a assinatura da função substitute vamos analisar cada um dos seus casos:

1. Substituição em Variáveis:

   substitute x n (Var y)
     | x == Y = n
     | otherwise = Var y
   

   Se a variável y é a mesma que estamos substituindo (x), retornamos o termo substituto n. Isto corresponde à regra 1 da substituição formal. Caso contrário, mantemos a variável original y inalterada, conforme a regra 2.

2. Substituição em Aplicações:

   substitute x n (App e1 e2) \, = App (substitute x n e1) (substitute x n e2)
   

   Aplicamos a substituição recursivamente em ambos os termos da aplicação. Isto reflete a regra 3 da substituição formal.

3. Substituição em Abstrações Lambda:

   substitute x n (Lam Y e)
     | Y == x = Lam Y e  -- Variável ligada é a mesma que estamos substituindo
     | Y `elem` freeVars n =  -- Risco de captura, aplicar redução alfa
         let y' = freshVar Y (n : e : [])
             e' = substitute Y (Var y') e
         in Lam y' (substitute x n e')
     | otherwise = Lam Y (substitute x n e)
   

   Este é o caso mais complexo e corresponde à regra 4 da substituição formal. Aqui, temos três subcasos:

   1. Se a variável ligada y é a mesma que estamos substituindo (x). Não fazemos nada, pois x está sombreada pela ligação de y.

   2. Se y está nas variáveis livres do termo substituto n: existe o risco de captura de variável livre. Para evitar isso, aplicamos a redução-$\alpha$, renomeando y para um novo nome y' que não cause conflito. Utilizamos a função freshVar para gerar um novo nome que não esteja nas variáveis livres ou ligadas das expressões envolvidas. Realizamos a substituição no corpo e após a renomeação.

   3. Caso contrário: substituímos recursivamente no corpo da abstração e, mantendo y inalterado.

4. Função para Variáveis Livres:

   freeVars :: Expr -> [String]
   freeVars (Var x) \, = [x]
   freeVars (App e1 e2) \, = freeVars e1 ++ freeVars e2
   freeVars (Lam x e) \, = filter (/= x) (freeVars e)
   

   Esta função calcula o conjunto de variáveis livres em uma expressão, essencial para evitar a captura de variáveis durante a substituição.

5. Função para Gerar Novos Nomes de Variáveis:

   freshVar :: String -> [Expr] -> String
   freshVar x exprs = head $ filter (`notElem` allVars) candidates
     where
       allVars = concatMap (\e -> freeVars e ++ boundVars e) exprs
       candidates = [x ++ show n | n <- [1..]]
   

   A função freshVar gera um novo nome de variável (y') que não está presente em nenhuma das variáveis livres ou ligadas das expressões fornecidas.

   Isso é crucial para a redução-$\alpha\,$, garantindo que o novo nome não cause conflitos.

6. Função para Variáveis Ligadas:

   boundVars :: Expr -> [String]
   boundVars (Var _) \, = []
   boundVars (App e1 e2) \, = boundVars e1 ++ boundVars e2
   boundVars (Lam x e) \, = x : boundVars e
   

   Esta função auxilia freshVar ao fornecer o conjunto de variáveis ligadas em uma expressão.

Implementando a redução-$\alpha$ no código, conseguimos evitar a captura de variáveis livres durante a substituição, conforme ilustrado nos exemplos anteriores. Vamos ver um exemplo de evasão de captura com renomeação de variável ligada. Considere o termo:

No código Haskell, este caso seria processado da seguinte forma:

1. Detectar o Risco de Captura: a variável ligada y está presente nas variáveis livres do termo substituto n (que é y). Portanto, precisamos aplicar a redução-$\alpha\,$.

2. Aplicar redução-$\alpha$: utilizamos freshVar para gerar um novo nome, digamos z. Renomeamos y para z na abstração, e substituímos y por z no corpo.

3. Realizar a Substituição: substituímos x por y no corpo renomeado.

4. Resultado: a expressão resultante é \lambda z.\;y, e y permanece livre.

Neste ponto, se a amável leitora se perdeu no Haskell, deve voltar as definições formais da substituição e tentar fazer o paralelo entre as definições formais e o código em Haskell. A importância desta implementação está na demonstração de como os conceitos teóricos do cálculo lambda podem ser traduzidos para código executável, fornecendo uma ponte entre a teoria e a prática.

2.4. Semântica Denotacional no Cálculo Lambda

A semântica denotacional é uma abordagem matemática para atribuir significados formais às expressões de uma linguagem formal, como o cálculo lambda.

Na semântica denotacional, cada expressão é mapeada para um objeto matemático que representa seu comportamento computacional. Isso fornece uma interpretação abstrata da computação, permitindo analisar e provar propriedades sobre programas com rigor.

No contexto do cálculo lambda, o domínio semântico é construído como um conjunto de funções e valores. O significado de uma expressão é definido por sua interpretação nesse domínio, utilizando um ambiente $\rho$ que associa variáveis a seus valores.

A interpretação denotacional é formalmente definida pelas seguintes regras:

1. Variáveis:

   \[[x]_\rho = \rho(x)\]

   O significado de uma variável $x$ é o valor associado a ela no ambiente $\rho\,$.Intuitivamente podemos entender esta regra como: quando encontramos uma variável $x\,$, consultamos o ambiente $\rho$ para obter seu valor associado.

   Exemplo: suponha um ambiente $\rho$ de tal forma que $\rho(x) \, = 5\,$.

   \[[x]_\rho = \rho(x) \, = 5\]

   Assim, o significado da variável $x$ é o valor $5$ no ambiente atual.

2. Abstrações Lambda:

   \[[\lambda x.\;E]_\rho = f\]

   O termo $f$ é uma função tal que:

   \[f(v) \, = [E]_{\rho[x \mapsto v]}\]

   Isso significa que a interpretação de $\lambda x.\;E$ é uma função que, dado um valor $v\,$, avalia o corpo $E$ no ambiente no qual $x$ está associado a $v\,$. Em bom português esta regra significa que uma abstração $\lambda x.\;E$ representa uma função anônima. Na semântica denotacional, mapeamos essa abstração para uma função matemática que, dado um valor de entrada, produz um valor de saída. Neste caso, teremos dois passos:

   1. Definição da Função $f$: A abstração é interpretada como uma função $f\,$. Neste caso, para cada valor de entrada $v\,$, calculamos o significado do corpo $e$ no ambiente estendido $\rho[x \mapsto v]\,$.

   2. Ambiente Estendido: O ambiente $\rho[x \mapsto v]$ é igual a $\rho\,$, exceto que a variável $x$ agora está associada ao valor $v\,$.

   Exemplo:

   Considere a expressão $\lambda x.\;x + 1\,$.

   Interpretação:

   \[[\lambda x.\;x + 1]_\rho = f\]

   O termo $f(v) \, = [x + 1]_{\rho[x \mapsto v]} = v + 1\,$.

   Significado: A abstração é interpretada como a função que incrementa seu argumento em 1.

3. Aplicações:

   \[[e_1\;e_2]_\rho = [e_1]_\rho\left([e_2]_\rho\right)\]

   O significado de uma aplicação $e_1\;e_2$ é obtido aplicando o valor da expressão $e_1$ (que deve ser uma função) ao valor da expressão $e_2\,$. Para interpretar uma aplicação $e_1\;e_2\,$, avaliamos ambas as expressões e aplicamos o resultado de $e_1$ ao resultado de $e_2\,$. Neste cenário temos três passos:

   1. Avaliar $e_1$: Obtemos $[e_1]_\rho\,$, que deve ser uma função.

   2. Avaliar $e_2$: Obtemos $[e_2]_\rho\,$, que é o argumento para a função.

   3. Aplicar: Calculamos $[e_1]\rho\left([e_2]\rho\right)\,$.

   Exemplo: considere a expressão $(\lambda x.\;x + 1)\;4\,$. Seguiremos três passos:

   Passo 1: Interpretar $\lambda x.\;x + 1\,$.

   \[[\lambda x.\;x + 1]_\rho = f, \quad \text{tal que} \quad f(v) \, = v + 1\]

   Passo 2: Interpretar $4\,$.

   \[[4]_\rho = 4\]

   Passo 3: Aplicar $f$ a $4\,$.

   \[[(\lambda x.\;x + 1)\;4]_\rho = f(4) \, = 4 + 1 = 5\]

   A expressão inteira é interpretada como o valor $5\,$.

2.4.1. Ambiente $\rho$ e Associação de Variáveis

O ambiente $\rho$ armazena as associações entre variáveis e seus valores correspondentes. Especificamente, $\rho$ é uma função que, dado o nome de uma variável, retorna seu valor associado. Ao avaliarmos uma abstração, estendemos o ambiente com uma nova associação utilizando $[x \mapsto v]\,$.

Exemplo de Atualização:

• Ambiente inicial: $\rho = { Y \mapsto 2 }$

• Avaliando $\lambda x.\;x + y$ com $x = 3$:

• Novo ambiente: $\rho’ = \rho[x \mapsto 3] = { Y \mapsto 2, x \mapsto 3 }$

• Avaliamos $x + y$ em $\rho’$:

A semântica denotacional facilita o entendimento do comportamento dos programas sem se preocupar com detalhes de implementação. Permite demonstrar formalmente que um programa satisfaz determinadas propriedades. Na semântica denotacional o significado de uma expressão complexa é construído a partir dos significados de suas partes.

A experta leitora deve concordar que exemplos, facilitam o entendimento e nunca temos o suficiente.

Exemplo 1: Com Variáveis Livres: considere a expressão $\lambda x.\;x + y\,$, na qual $y$ é uma variável livre.

• Ambiente Inicial: $\rho = { Y \mapsto 4 }$
• Interpretação da Abstração:

• Aplicação: Avaliando $f(6)\,$, obtemos $6 + 4 = 10\,$.

Exemplo 2: Aninhamento de Abstrações. Considere $\lambda x.\;\lambda y.\;x + y\,$.

• Interpretação:

  • Primeiro, interpretamos a abstração externa:
  \[[\lambda x.\;\lambda y.\;x + y]_\rho = f, \quad \text{tal que} \quad f(v) \, = [\lambda y.\;x + y]_{\rho[x \mapsto v]}\]
  • Agora, interpretamos a abstração interna no ambiente estendido:
  \[f(v) \, = g, \quad \text{tal que} \quad g(w) \, = [x + y]_{\rho[x \mapsto v, Y \mapsto w]} = v + w\]

• Aplicação:

  • Avaliando $((\lambda x.\;\lambda y.\;x + y)\;3)\;5$:

    • $f(3) \, = g\,$, para $g(w) \, = 3 + w$
    • $g(5) \, = 3 + 5 = 8$

A semântica denotacional oferece um sistema matemático de atribuir significados às expressões do cálculo lambda. Ao mapear expressões para objetos matemáticos, valores e funções, podemos analisar programas de forma precisa e rigorosa. Entender essas regras permite uma compreensão mais profunda de como funções e aplicações funcionam no cálculo lambda.

Conceitos da semântica denotacional são fundamentais em linguagens funcionais modernas, como Haskell e OCaml.

Ferramentas baseadas em semântica denotacional podem ser usadas para verificar propriedades de programas, como terminação e correção.

Finalmente, a atenta leitora pode perceber que a semântica denotacional permite pensar em expressões lambda como funções matemáticas. Já a semântica operacional foca nos passos da computação.

Observe que a Semântica Operacional é geralmente mais adequada para descrever a execução procedural de linguagens que usam passagem por referência, pois permite capturar facilmente como os estados mudam durante a execução. Por outro lado, a Semântica Denotacional é mais alinhada com linguagens puras, que preferem passagem por cópia, evitando efeitos colaterais e garantindo que o comportamento das funções possa ser entendido matematicamente.

Existe uma conexão direta entre a forma como a semântica de uma linguagem é modelada e o mecanismo de passagem de valor que a linguagem suporta. Linguagens que favorecem efeitos colaterais tendem a ser descritas de forma mais natural por semântica operacional, enquanto aquelas que evitam efeitos colaterais são mais bem descritas por semântica denotacional.

No caso do cálculo lambda, a semântica denotacional é preferida. O cálculo lambda é uma linguagem puramente funcional sem efeitos colaterais. A semântica denotacional modela suas expressões como funções matemáticas. Isso está em alinhamento com a natureza do cálculo lambda. Embora a semântica operacional possa descrever os passos de computação, a semântica denotacional fornece uma interpretação matemática abstrata adequada para linguagens que evitam efeitos colaterais.

3. Técnicas de Redução, Confluência e Combinadores

As técnicas de redução no cálculo lambda são mecanismos para simplificar e avaliar expressões lambda. Estas incluem a redução-$\alpha$ e a redução beta, que são utilizadas para manipular e computar expressões lambda. Essas técnicas são relevantes tanto para a teoria quanto para a implementação prática de sistemas baseados em lambda, incluindo linguagens de programação funcional. A compreensão dessas técnicas permite entender como funções são definidas, aplicadas e transformadas no contexto do cálculo lambda. A redução-$\alpha$ lida com a renomeação de variáveis ligadas, enquanto a redução beta trata da aplicação de funções a argumentos.

O Teorema de Church-Rosser, conhecido como propriedade de confluência local, estabelece a consistência do processo de redução no cálculo lambda. currying, por sua vez, é uma técnica que transforma funções com múltiplos argumentos em uma sequência de funções de um único argumento. Os combinadores, como S, K, e I, são expressões lambda sem variáveis livres que permitem a construção de funções complexas a partir de blocos básicos. Esses conceitos complementam as técnicas de redução e formam a base teórica para a manipulação e avaliação de expressões no cálculo lambda.

3.1. Redução Alfa

A redução-$\alpha\,$, ou alpha reduction, é o processo de renomear variáveis ligadas em termos lambda, para preservar o comportamento funcional dos termos. Dois termos são equivalentes sob redução-$\alpha$ se diferirem unicamente nos nomes de suas variáveis ligadas.

A atenta leitora deve considerar um termo lambda $\lambda x.\;E\,$, na qual $E$ é o corpo do termo. A redução-$\alpha$ permitirá a substituição da variável ligada $x$ por outra variável, digamos $y\,$, desde que $y$ não apareça livre em $E\,$. O termo resultante é $\lambda y.\;E[x \mapsto y]\,$. Neste caso, a notação $E[x \mapsto y]$ indica a substituição de todas as ocorrências de $x$ por $y$ em $E\,$. Formalmente:

Seja $\lambda x.\;E$ um termo lambda, teremos:

com a condição:

O termo $\text{FV}(E)$ representa o conjunto de variáveis livres em $E\,$, e $E[x \mapsto y]$ indica o termo resultante da substituição de todas as ocorrências da variável $x$ por $y$ em $E\,$, respeitando as ligações de variáveis para evitar a captura. A substituição $E[x \mapsto y]$ é definida formalmente por indução na estrutura de $E\,$. As possibilidades que devemos analisar são:

1. Se $E$ é uma variável, e for igual a $x\,$, a substituição resulta em $y$; caso contrário, $E[x \mapsto y]$ é o próprio $E\,$.

2. Se $E$ é uma aplicação $E_1\;E_2\,$, a substituição é aplicada a ambos os componentes, ou seja, $E[x \mapsto y] = E_1[x \mapsto y]\;E_2[x \mapsto y]\,$.

3. Se $E$ é uma abstração $\lambda z.\;E’\,$, a situação depende da relação entre $z$ e $x\,$.

   • Se $z$ é igual a $x\,$, então $E[x \mapsto y]$ é $\lambda z.\;E’\,$, pois $x$ está ligada por $\lambda z$ e não deve ser substituída dentro de seu próprio escopo.

   • Se $z$ é diferente de $x\,$, e $y$ não aparece livre em $E’$ e $z$ é diferente de $y\,$, então $E[x \mapsto y]$ é $\lambda z.\;E’[x \mapsto y]\,$.

4. Se $y$ aparece livre em $E’$ ou $z$ é igual a $y\,$, é necessário renomear a variável ligada $z$ para uma nova variável $w$ que não apareça em $E’$ nem em $y\,$, reescrevendo $E$ como $\lambda w.\;E’[z \mapsto w]$ e então procedendo com a substituição: $E[x \mapsto y] = \lambda w.\;E’[z \mapsto w][x \mapsto y]\,$.

Finalmente temos que a condição $y \notin \text{FV}(E)$ é a forma de evitar a captura de variáveis livres durante a substituição, garantindo que o conjunto de variáveis livres permaneça inalterado e que a semântica do termo seja preservada.

Usamos A redução-$\alpha$ para evitar a captura de variáveis livres durante a substituição na redução beta. Ao substituir um termo $N$ em um termo $E\,$, é possível que variáveis livres em $N$ tornem-se ligadas em $E\,$, o que irá alterar o significado semântico do termo. Para evitar isso, é necessário renomear as variáveis ligadas em $E$ para novas variáveis que não conflitem com as variáveis livres em $N\,$.

Exemplo 1: Considere o termo:

Este termo é uma aplicação de função com duas funções identidade. Podemos começar com a estrutura do termo: uma função externa $\lambda x.\;x$ aplicada a um argumento que é uma função, $\lambda y.\;y\,$.

Uma vez que entendemos a estrutura, podemos fazer a análise das variáveis ligadas. Na função externa, $(\lambda x.\;x)\,$, $x$ é uma variável ligada. No argumento, $(\lambda y.\;y)\,$, $y$ é uma variável ligada.

Nosso próximo passo é verificar o escopo das variáveis. No termo original, $x$ está ligada no escopo de $\lambda x.\;x$ e $y$ está ligada no escopo de $\lambda y.\;y$

Em resumo, no termo original, $(\lambda x.\;x)\;(\lambda y.\;y)\,$, as variáveis ligadas $x$ e $y$ estão em escopos diferentes. Não há sobreposição ou conflito entre os escopos de $x$ e $y\,$. Ou seja, a substituição de $x$ por $(\lambda y.\;y)\,$, durante a aplicação, não causará captura de variáveis. Neste caso, não há necessidade de aplicar a redução-$\alpha\,$. As variáveis $x$ e $y$ podem permanecer com seus nomes originais sem causar ambiguidade ou conflito.

Neste ponto, já sabemos que não há necessidade de redução-$\alpha$ o que simplifica o processo de avaliação do termo. Logo, a aplicação, redução-$beta\,$, pode ser aplicada diretamente. Neste caso, substituímos todas as ocorrências de $x$ no corpo da abstração externa pelo argumento $\lambda y.\;y\,$, como $x$ aparece uma vez no corpo, o resultado é simplesmente $\lambda y.\;y\,$.

Este exemplo ilustra uma situação em que, apesar de termos múltiplas variáveis ligadas ($x$ e $y$), suas definições em escopos distintos e não sobrepostos eliminam a necessidade de redução-$\alpha\,$.

Com o Exemplo 2 podemos perceber que a necessidade de redução-$\alpha$ não depende somente da presença de variáveis ligadas, mas depende de como seus escopos interagem no termo como um todo.

Exemplo 2: Considere o termo:

Observe que neste termo, a variável $x$ está ligada duas vezes em escopos diferentes, duas abstrações lambda. Para evitar confusão, podemos aplicar a redução-$\alpha$ para renomear uma das variáveis ligadas. Podemos aplicar na abstração interna ou na abstração externa. Vejamos:

1. Renomear a variável ligada interna:

   \[\lambda x.\;\lambda x.\;x \to_\alpha \lambda x.\;\lambda z.\;z\]

   Esta escolha é interessante por alguns motivos. O primeiro é que esta redução preserva a semântica do termo mantendo o significado original da função externa intacto. A redução da abstração interna preserva o escopo mínimo de mudança. Alterando o escopo mais interno, minimizamos o impacto em possíveis referências externas.

   A escolha pela abstração interna mantém a clareza da substituição. Durante a aplicação, redução-$beta\,$, ficará evidente que $y$ irá substituir o $x$ externo, enquanto $z$ permanece inalterado. Por fim, a redução da abstração interna é consistente com as práticas de programação e reflete o princípio de menor surpresa, mantendo variáveis externas estáveis. Por último, a escolha da abstração interna previne a captura acidental de variáveis livres.

2. Renomear a variável ligada externa:

   \[\lambda x.\;\lambda x.\;x \to_\alpha \lambda z.\;\lambda x.\;x\]

   A escolha pela abstração externa implica no risco de alteração semântica, correndo o risco de mudar o comportamento se o termo for parte de uma expressão maior que referencia $x\,$. Outro risco está na perda de informação estrutural. Isso será percebido após a aplicação, redução-$\beta\,$, ($\lambda x.\;x$), perde-se a informação sobre a abstração dupla original. Existe ainda possibilidade de criarmos uma confusão de escopos que pode acarretar uma interpretações errônea sobre qual variável está sendo referenciada em contextos mais amplos.

   Há uma razão puramente empírica. A escolha pela abstração externa contraria as práticas comuns ao cálculo lambda, no qual as variáveis externas geralmente permanecem estáveis. Por fim, a escolha pela abstração externa reduz a rastreabilidade das transformações em sistemas de tipos ou em sistemas de análise estáticas.

A perspicaz leitora deve ter percebido o esforço para justificar a aplicação da redução-$\alpha$ a abstração interna. Agora que a convenci, podemos fazer a aplicando, β-redução, após a abordagem 1:

Esta redução resulta em uma expressão que preserva a estrutura essencial do termo original, mantendo a abstração interna intacta e substituindo a variável externa, conforme esperado na semântica do cálculo lambda.

3.1.1. Formalização da Equivalência Alfa

A equivalência alfa é um conceito do cálculo lambda que estabelece quando dois termos são considerados essencialmente idênticos, diferindo exclusivamente nos nomes de suas variáveis ligadas. Formalmente dizemos que dois termos lambda $M$ e $N$ são considerados alfa-equivalentes, denotado por $M \equiv_\alpha N\,$, se um pode ser obtido do outro por meio de uma sequência finita de renomeações consistentes de variáveis ligadas.

Podemos definir a equivalência alfa considerando as três estruturas básicas do cálculo lambda:

1. Variáveis: $x \equiv_\alpha x$

2. Aplicação: Se $E_1 \equiv_\alpha F_1$ e $E_2 \equiv_\alpha F_2\,$, então $(E_1\;E_2) \equiv_\alpha (F_1\;F_2)$

3. Abstração: Se $E \equiv_\alpha F[y/x]$ e $y$ não ocorre livre em $E\,$, então $\lambda x.\;E \equiv_\alpha \lambda y. F$

O termo $F[y/x]$ indica a substituição de todas as ocorrências livres de $x$ por $y$ no corpo $F\,$.

Para que a equivalência alfa seja válida, precisamos seguir três regras básicas: garantir que as variáveis ligas a um termo lambda sejam renomadas; ao renomear uma variável ligada aplicamos a renomeação a todas as ocorrências da variável dentro de seu escopo, corpo $E\,$, devem ser substituídas pelo novo nome; e finalmente, o novo nome escolhido para a variável ligada não deve aparecer livre no corpo $E$ depois que a substituição for aplicada.

Do ponto de vista da análise relacional, a relação $\equiv_\alpha$ é uma relação de equivalência, o que significa que ela possui as propriedades de: Reflexividade, significando que para todo termo $M\,$, $M \equiv_\alpha M\,$. Ou seja, todo termo é alfa equivalente a si mesmo; Simetria, se $M \equiv_\alpha N\,$, então $N \equiv_\alpha M\,$. Todos os termos equivalentes, são equivalentes entre si; e Transitividade, se $M \equiv_\alpha N$ e $N \equiv_\alpha P\,$, então $M \equiv_\alpha P\,$. Se dois termos, $M$ e $N$ são equivalentes entre si e um deles e equivalente a um terceiro termo, então o outro será equivalente ao terceiro termo, como pode ser visto na Figura 3.1.1.A.

Diagrama apresentando a transitividade da $\equiv_\alpha$.{: class=”legend”}

A amável leitora pode estudar os exemplos a seguir para entender os conceitos da $\equiv_\alpha$.

Exemplo 1:

Neste termo, $E$ representa o corpo da função, e $E[y/x]$ representa a substituição de $x$ por $y$ em $E\,$.

Exemplo 2:

Aqui $E[a/x][b/y]$ representa o corpo $E$ com $x$ substituído por $a$ e $y$ por $b\,$.

Exemplo 3:

Essa expressão indica que a abstração lambda $\lambda x.\;E$ é alfa-equivalente à abstração $\lambda z.\;E[z/x]\,$, no qual a variável ligada $x$ foi substituída por $z\,$. Esse processo de renomeação não afeta as variáveis livres em $E\,$. Se em $E$ existir uma variável $y\,$, esta variável seria livre e não seria afetada.

Exemplo 4: Renomeação Inválida. Considere a expressão:

Uma tentativa inválida de renomeação seria:

Esta renomeação é inválida porque: Viola a regra de captura de variáveis: ao renomear $y$ para $x\,$, estamos potencialmente capturando ocorrências livres de $x$ que possam existir em $E$; Provoca Perda de distinção: as variáveis $x$ e $y\,$, que originalmente eram distintas, agora se tornaram a mesma variável, alterando potencialmente o significado da expressão; e Altera a estrutura de escopo: o escopo da variável $x$ externa foi efetivamente estendido para incluir o que antes era o escopo de $y\,$. Para ilustrar com um exemplo concreto desse problema, considere:

A renomeação inválida resultaria em:

Observe que o significado da expressão mudou. Na expressão original, $x$ e $y$ poderiam ter valores diferentes, mas na versão renomeada incorretamente, elas são forçadas a ter o mesmo valor.

Uma renomeação válida seria:

Aqui, renomeamos $y$ para $z\,$, mantendo a distinção entre as variáveis e preservando a estrutura e o significado da expressão original.

3.1.1.1. Importância para a redução-$beta$

A equivalência alfa é impacta na correção da aplicação da redução-$beta\,$. Vamos analisar o seguinte exemplo:

Se aplicássemos a redução-$beta$ diretamente, obteríamos $\lambda y.\;E[y/x]\,$, o que poderia mudar o significado da expressão se $y$ ocorrer livre em $E\,$. Para evitar isso, primeiro aplicamos uma redução-$\alpha$:

Agora podemos aplicar a redução-$beta$ com segurança:

Este exemplo ilustra como a equivalência alfa permite o uso seguro da redução beta e da substituição no cálculo lambda, preservando o significado pretendido do corpo $E$ da função original.

3.1.3. Convenções Práticas: Convenção de Variáveis de Barendregt

Na prática, a redução-$\alpha$ é frequentemente aplicada implicitamente durante as substituições no cálculo lambda. A convenção das variáveis de Barendregt⁷ estabelece que todas as variáveis ligadas em um termo devem ser escolhidas de modo que sejam distintas entre si e distintas de quaisquer variáveis livres presentes no termo. Essa convenção elimina a necessidade de renomeações explícitas frequentes e simplifica a manipulação dos termos lambda.

A partir da Convenção de Barendregt, a definição de substituição pode ser simplificada. Em particular, ao realizar a substituição $[N/x]\;(\lambda y.\;M)\,$, podemos escrever:

Assumindo implicitamente que, se necessário, a variável ligada $y$ é renomeada para evitar conflitos, garantindo que $y \neq x$ e que $y$ não apareça livre em $N\,$. Isso significa que não precisamos nos preocupar com a captura de variáveis livres durante a substituição, pois a convenção assegura que as variáveis ligadas são sempre escolhidas de forma apropriada. Permitido que tratemos os termos alfa-equivalentes como se fossem idênticos. Por exemplo, podemos considerar os seguintes termos como iguais:

Ambos representam a mesma função, diferindo unicamente nos nomes das variáveis ligadas. Essa abordagem simplifica significativamente a manipulação de termos lambda, pois não precisamos constantemente lidar com conflitos de nomes ou realizar reduções alfa explícitas. Podemos focar nas reduções beta e na estrutura funcional dos termos, sabendo que a escolha dos nomes das variáveis ligadas não afeta o comportamento das funções representadas.

3.2. redução Beta

A redução beta é o mecanismo de computação do cálculo lambda que permite simplificar expressões por meio da aplicação de funções aos seus argumentos. As outras reduções $\beta$ e $\eta$ são mecanismos de transformação que facilitam, ou possibilitam, a redução-$beta\,$.Formalmente, a redução beta é definida como:

A notação $[x/N]M$ representa a substituição de todas as ocorrências livres da variável $x$ no termo $E$ pelo termo $N\,$. Eventualmente, quando estudamos semântica denotacional, ou provas formais, usamos a notação $E[x := y]\,$.

A substituição indicada em uma redução-$beta$ deve ser realizada com cuidado para evitar a captura de variáveis livres em $N$ que possam se tornar ligadas em $E$ após a substituição. Para evitar a captura de varáveis livres, pode ser necessário realizar uma redução-$\alpha$ antes de começar a redução beta, renomeando variáveis ligadas em $E$ que possam entrar em conflito com variáveis livres em $N\,$, Figura 3.2.A.

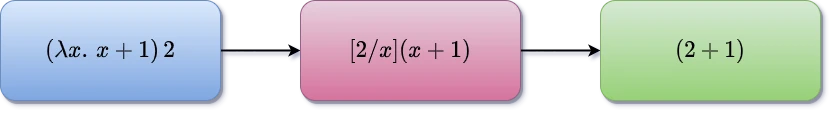3.2.A: Exemplo de Redução Beta

Considere, por exemplo, o termo $E = (\lambda y.\;x + y)$ e o objetivo de substituir $x$ por $N = y\,$. Se fizermos a substituição diretamente, obteremos:

Nesse caso, a variável livre $y$ em $N$ tornou-se ligada devido ao $\lambda y$ em $E\,$, resultando em captura de variável e alterando o significado original da expressão. Para evitar a captura, aplicamos uma redução-$\alpha$ ao termo $E\,$, renomeando a variável ligada $y$ para uma nova variável que não apareça em $N\,$, como $z$:

Agora, ao substituir $x$ por $y\,$, obtemos:

A variável livre $y$ permanece livre após a substituição, e a captura é evitada. Outro exemplo é o termo $E = (\lambda x.\;\lambda y.\;x + y)$ com $N = y\,$. Tentando substituir diretamente, temos:

Aqui, a variável livre $y$ em $N$ foi capturada pelo $\lambda y$ interno. Para prevenir isso, realizamos uma redução-$\alpha$ renomeando a variável ligada $y$ para $z$:

Procedendo com a substituição:

Assim, a variável livre $y$ não é capturada, preservando o significado da expressão original.

Em suma, ao realizar a substituição $[x/N]E\,$, é essencial garantir que as variáveis livres em $N$ permaneçam livres após a substituição e não sejam capturadas por variáveis ligadas em $E\,$. A persistente leitora deve avaliar os exemplos a seguir:

Exemplo 1: considere a expressão:

Aplicando a redução beta:

Neste caso, substituímos $x$ por $3$ no corpo da função $x + y\,$, resultando em $3 + y\,$. A variável $y$ permanece inalterada por ser uma variável livre.

Exemplo 2: se houver risco de captura de variáveis, é necessário realizar uma redução-$\alpha$ antes. Por exemplo:

Aplicando a redução beta diretamente:

Aqui, a variável livre $y$ no argumento foi capturada pela variável ligada $y$ na função interna. Para evitar isso, realizamos uma redução-$\alpha$ renomeando a variável ligada $y$ para $z$:

Agora podemos aplicar a redução beta:

Assim, evitamos a captura da variável livre $y\,$, mantendo o significado original da expressão.

Exemplo 3: considere a expressão:

Aplicando a redução beta:

Aqui, o valor $2$ é substituído pela variável $x$ na expressão $x + 1\,$, resultando em $2 + 1 = 3\,$.

Exemplo 4: um exemplo mais complexo envolvendo uma função de ordem superior:

Reduzindo passo a passo:

Neste exemplo, aplicamos primeiro a função $(\lambda f.\lambda x.\;f\;(f\;x))$ ao argumento $(\lambda y.\;y \times 2)\,$, resultando em uma expressão que aplica duas vezes a função de duplicação ao número $3\,$, obtendo $12\,$.

3.3. Redução Eta

A redução-$\eta$ é uma das três formas de redução no cálculo lambda, juntamente com as reduções alfa e beta. A redução-$\eta$ captura a ideia de extensionalidade, permitindo simplificar termos que representam a mesma função pelo comportamento externo. Formalmente, a redução-$\eta$ é definida pela seguinte regra:

Neste caso, esta expressão é formada por: uma função $\lambda x.\;f\;x$ que recebe um argumento $x$ e aplica a função $f$ a $x$; $\text{FV}(f)$ representa o conjunto de variáveis livres em $f$ e a condição $x \notin \text{FV}(f)$ garante que $x$ não aparece livre em $f\,$, evitando a captura de variáveis.

A redução-$\eta$ permite eliminar a abstração $\lambda x$ quando a função aplica $f$ diretamente a $x\,$, resultando que $\lambda x.\;f\;x$ é equivalente a comportamentalmente a $f$. Isso ocorre quando $x$ não aparece livre em $f\,$, garantindo que a eliminação da abstração não altera o significado do termo. Podemos dizer que a redução-$\eta$ expressa o princípio de que duas funções são iguais se, para todos os argumentos, elas produzem os mesmos resultados. Se uma função $\lambda x.\;f\;x$ aplica $f$ diretamente ao seu argumento $x\,$, e $x$ não aparece livre em $f\,$, então $\lambda x.\;f\;x$ pode ser reduzido a $f\,$.

Exemplo 1: Considere o termo:

Se $f = \lambda y.\;y + 2$ e $x$ não aparece livre em $f\,$, a redução-$\eta$ pode ser aplicada:

Assim, $\lambda x.\;f\;x$ reduz-se a $f\,$.

Exemplo 2: Considere o termo:

Como $x$ não aparece livre em $f = \lambda y.\;y^2\,$, a redução-$\eta$ pode ser aplicada:

Portanto, $\lambda x.\;(\lambda y.\;y^2)\;x$ reduz-se a $\lambda y.\;y^2\,$.

Se $x$ aparece livre em $f\,$, a redução-$\eta$ não é aplicável, pois a eliminação de $\lambda x$ alteraria o comportamento do termo. Por exemplo, se $f = \lambda y.\;x + y\,$. Neste caso, $x$ é uma variável livre em $f\,$, então:

Neste caso, não é possível aplicar a redução-$\eta$ para obter $f\,$, pois $x$ aparece livre em $f\,$, e remover $\lambda x$ deixaria $x$ indefinida.

A condição $x \notin \text{FV}(f)$ é crucial. Se $x$ aparecer livre em $f\,$, a redução-$\eta$ não pode ser aplicada, pois a remoção da abstração $\lambda x$ poderia alterar o significado do termo.

Exemplo Contrário: Considere a expressão:

Aqui, $x$ aparece livre no corpo $x\;x\,$. Não podemos aplicar a redução-$\eta$ para obter $x\,$, pois isso alteraria o comportamento da função.

3.3.1. Propriedade de Extensionalidade

A redução-$\eta$ está relacionada ao conceito de extensionalidade em matemática. Neste conceito, duas funções são consideradas iguais se produzem os mesmos resultados para todos os argumentos. No cálculo lambda, a redução-$\eta$ formaliza esse conceito, permitindo a simplificação de funções que são extensionais.

Em matemática, o conceito de extensionalidade refere-se à ideia de que dois objetos são considerados iguais se têm as mesmas propriedades externas ou observáveis. No contexto das funções, a extensionalidade implica que duas funções $f$ e $g$ são consideradas iguais se, para todo argumento $x$ em seu domínio comum, $f(x) \, = g(x)\,$. Isso significa que a identidade de uma função é determinada pelos seus valores de saída para cada entrada possível, e não pela sua definição interna ou pela forma como é construída.

A extensionalidade é um princípio em várias áreas da matemática, incluindo teoria dos conjuntos e lógica matemática. Na teoria dos conjuntos, o axioma da extensionalidade afirma que dois conjuntos são iguais se e somente se contêm exatamente os mesmos elementos. No cálculo lambda e na programação funcional, a extensionalidade se manifesta através de conceitos como a redução-$\eta\,$, que permite tratar funções que produzem os mesmos resultados para todas as entradas como equivalentes, independentemente de suas estruturas internas.

Para ilustrar o conceito de extensionalidade e sua relação com a redução-$\eta\,$, a esforçada leitora deve considerar os seguintes exemplos:

Exemplo 1: Suponha que temos duas funções no cálculo lambda:

e

Embora $f$ e $g$ tenham definições diferentes, podemos demonstrar que elas produzem o mesmo resultado para qualquer valor de $x$:

Portanto, para todo $x\,$, $f(x) \, = g(x)\,$, o que significa que $f$ e $g$ são extensionais, apesar de suas diferentes expressões internas.

Exemplo 2: Considere as funções:

Se $x$ não aparece livre em $f\,$, a redução-$\eta$ nos permite afirmar que $h$ é equivalente a $k$:

Isso mostra que, embora $h$ seja definido como uma função que aplica $f$ a $x\,$, ela é extensionamente igual a $f$ em si, reforçando o princípio de que a forma interna da função é menos relevante do que seu comportamento externo.

Exemplo 3: No contexto da programação funcional, suponha que temos a seguinte função em Haskell:

-- Definição explícita
doubleList :: [Int] -> [Int]
doubleList xs = map (\x -> x * 2) xs

Aplicando a redução-$\eta$ e considerando o conceito de extensionalidade, podemos simplificar a função:

-- Após a redução eta
doubleList :: [Int] -> [Int]
doubleList = map (* 2)

Apesar das diferenças na implementação, ambas as versões de doubleList produzem os mesmos resultados para qualquer lista de inteiros fornecida, demonstrando que são extensionais.

Exemplo 4: Na teoria dos conjuntos, considere:

Ambos os conjuntos $A$ e $B$ contêm exatamente os mesmos elementos. Pelo axioma da extensionalidade, concluímos que $A = B\,$, mesmo que suas definições sejam diferentes.

Em resumo, a extensionalidade nos permite focar no comportamento observável das funções ou conjuntos, em vez de suas definições internas. No cálculo lambda, a redução-$\eta$ é a ferramenta que formaliza esse princípio, simplificando termos que representam funções com o mesmo efeito para todos os argumentos. Ao aplicar a redução-$\eta\,$, estamos essencialmente afirmando que a forma como a função é construída é irrelevante se seu comportamento externo permanece inalterado.

3.3.2. Expansão $\eta$

Além da redução-$\eta\,$, existe a expansão $\eta$, que é a operação inversa da redução-$\eta$:

A expansão $\eta$ pode ser útil para transformar termos em formas que facilitam outras reduções ou para provar equivalências entre funções. Neste caso, a equivalência lambda ($\equiv$) é a relação de equivalência gerada pelas reduções alfa, beta e $\eta\,$. Dois termos $M$ e $N$ são equivalentes lambda ($M \equiv N$) se podem ser transformados um no outro por uma sequência finita de reduções e expansões alfa, beta e $\eta\,$.

Exemplo: considere a definição de uma função identidade:

E uma função $F$ definida como:

Aplicando a redução-$\eta$ a $F$ podemos observar que $I\;x = (\lambda y.\;y)\;x \to_\beta x\,$, ou seja:

Ou seja, $F$ pode ser reduzido a $I\,$. No entanto, usando a redução-$\eta$ diretamente:

Como $x$ não aparece livre em $I\,$, podemos aplicar a redução-$\eta$ para obter $F = I\,$.

3.3.3. Relação entre redução-$\eta$ e outras Formas de Redução

No cálculo lambda, as reduções alfa, beta e $\eta$ formam um conjunto integrado de transformações que permitem manipular e simplificar expressões lambda. Cada uma dessas reduções desempenha um papel específico, mas elas frequentemente interagem e complementam-se mutuamente.

Vamos começar com a redução-$\alpha\,$, que lida com a renomeação de variáveis ligadas, pode ser necessária antes de aplicar a redução-$\eta$ para evitar conflitos de nomes. Por exemplo:

Neste caso, a redução-$\alpha$ foi aplicada primeiro para renomear $y$ para $z\,$, evitando a captura de variável, antes de aplicar a redução-$\eta\,$.

A interação entre redução-$\eta$ e beta é particularmente interessante. Em alguns casos, a redução-$\eta$ pode simplificar expressões após a aplicação da redução beta:

Aqui, a redução beta é aplicada primeiro, seguida pela redução-$\eta$ para simplificar ainda mais a expressão.

Nesta interação entre as reduções precisamos tomar cuidado com a ordem de aplicação das reduções pode afetar o resultado e a eficiência do processo de redução. Em linhas gerais, podemos seguir as seguintes regras:

1. A redução-$\alpha$ é aplicada conforme necessário para evitar conflitos de nomes.

2. A redução beta é frequentemente aplicada após a aplicação alfa para realizar computações.

3. A redução-$\eta$ é aplicada para simplificar a estrutura da função após as reduções beta.

O processo de aplicar todas as reduções possíveis (alfa, beta e $\eta$) até que nenhuma outra redução seja possível é chamado de normalização. A forma normal de um termo lambda é única, se existir, independentemente da ordem das reduções, graças ao Teorema de Church-Rosser.

Exemplo Integrado: Considere a seguinte expressão:

Podemos aplicar as reduções na seguinte ordem:

1. Redução beta: $(\lambda x. \lambda y.\;x) (\lambda z.\;z) \to_\beta \lambda y. (\lambda z.\;z)$

2. redução-$\eta$: $\lambda y. (\lambda z.\;z) \to_\eta \lambda z.\;z$

O resultado\;$\lambda z.\;z\,$, é a função identidade, obtida através da aplicação combinada de reduções beta e $\eta\,$.

Entender a interação entre estas formas de redução é crucial para manipular eficientemente expressões lambda e para compreender a semântica de linguagens de programação funcional baseadas no cálculo lambda.

3.3.4. Relação entre a redução-$\eta$ e a Programação Funcional

A redução-$\eta$ é frequentemente utilizada em programação funcional para simplificar código e torná-lo mais conciso. Em Haskell, essa técnica é particularmente comum. Vejamos alguns exemplos práticos:

Exemplo 1: Simplificação de Funções

Em Haskell, podemos usar a redução-$\eta$ para simplificar definições de funções:

-- Antes da redução-$\eta$
addOne :: Int -> Int
addOne x = (+ 1) x

-- Após a redução-$\eta$
addOne :: Int -> Int
addOne = (+ 1)

Neste exemplo, definimos uma função addOne que adiciona $1$ a um número inteiro. Vamos entender como a redução-$\eta$ é aplicada aqui:

Na versão antes da redução-$\eta$: addOne x = (+ 1) x define uma função que toma um argumento x. Enquanto (+ 1) é uma função parcialmente aplicada em Haskell, equivalente a \y -> Y + 1. A função addOne aplica (+ 1) ao argumento x.

A redução-$\eta$ nos permite simplificar esta definição: observamos que x aparece como o último argumento tanto no lado esquerdo (addOne x) quanto no lado direito ((+ 1) x) da equação. A redução-$\eta$ permite remover este argumento x de ambos os lados.

Após a redução-$\eta$ temos addOne = (+ 1) é a forma simplificada. Isso significa que addOne é definida como sendo exatamente a função (+ 1).

No cálculo lambda, temos:

Em Haskell, isso se traduz em remover o argumento $x$ e a aplicação deste argumento. Graças a redução-$\eta\,$, as duas versões de addOne são funcionalmente idênticas. Para qualquer entrada n, tanto addOne n quanto (+ 1) n produzirão o mesmo resultado.

Exemplo 2: Composição de Funções

-- Antes da redução-$\eta$
compose :: (b -> c) -> (a -> b) -> a -> c
compose f g x = f (g x)

-- Após a redução-$\eta$
compose :: (b -> c) -> (a -> b) -> a -> c
compose f g = f . g

Este exemplo demonstra como a redução-$\eta$ pode simplificar a definição de uma função de composição. Detalhando temos:

1. Antes da redução-$\eta$ temos: - compose f g x = f (g x) define uma função que toma três argumentos: f, g, e x. Neste caso, f é uma função de tipo b -> c, g é uma função de tipo a -> b e x é um valor de tipo a. Ou seja, a função aplica g a x, e então aplica f ao resultado.

2. Aplicando a redução-$\eta$ observamos que x aparece como o último argumento tanto no lado esquerdo (compose f g x) quanto no lado direito (f (g x)) da equação. A redução-$\eta$ nos permite remover este argumento x de ambos os lados.

3. Após a redução-$\eta$ temos: compose f g = f . g é a forma simplificada. Neste caso, o operador . em Haskell representa a composição de funções. (f . g) é equivalente a \x -> f (g x).

No cálculo lambda, temos:

O termo $\circ$ representa a composição de funções. Em Haskell, isso se traduz em remover o argumento x e usar o operador de composição .. Desta forma, as duas versão de compose são funcionalmente idênticas. Ou seja, para quaisquer funções f e g e um valor x, tanto compose f g x quanto (f . g) x produzirão o mesmo resultado.

A versão após a redução-$\eta$ expressa mais diretamente o conceito de composição de funções. Já que, elimina a necessidade de mencionar explicitamente o argumento x, focando na relação entre as funções f e g. A redução-$\eta$ neste caso, não somente simplifica a sintaxe, mas destaca a natureza da composição de funções como uma operação sobre funções, em vez de uma operação sobre os valores que essas funções processam.

Exemplo 3: Funções de Ordem Superior

-- Antes da redução-$\eta$
map' :: (a -> b) -> [a] -> [b]
map' f xs = map f xs

-- Após a redução-$\eta$
map' :: (a -> b) -> [a] -> [b]
map' = map

Este exemplo demonstra como a redução-$\eta$ pode simplificar a definição de uma função que envolve outra função de ordem superior. Detalhando o processo temos:

1. Antes da redução-$\eta$: map' f xs = map f xs define uma função map' que toma dois argumentos: f (uma função) e xs (uma lista). Esta função simplesmente aplica a função map padrão do Haskell com os mesmos argumentos.

2. Aplicando a redução-$\eta$: observamos que tanto f quanto xs aparecem na mesma ordem no lado esquerdo e direito da equação. A redução-$\eta$ nos permite remover ambos os argumentos.

3. Após a redução-$\eta$: map' = map é a forma simplificada. Isso define map' como sendo exatamente a função map padrão do Haskell.

No cálculo lambda, temos:

Cada passo remove um argumento, resultando na função map por si só.

Do ponto de vista da equivalência funcional temos: map' f xs e map f xs são funcionalmente idênticas para quaisquer f e xs. Finalmente, a versão reduzida map' = map expressa que map' é exatamente a mesma função que map. Esta redução mostra que map' não adiciona nenhuma funcionalidade extra à map. Em um cenário real, se não houver necessidade de uma função wrapper, a definição de map' poderia ser completamente omitida, usando-se diretamente map.

A redução-$\eta$ neste caso, revela que map' é um alias para map. Isso demonstra como a redução-$\eta$ pode ajudar a identificar e eliminar definições de funções redundantes, levando a um código mais conciso e direto.

Exemplo 4: Funções Parcialmente Aplicadas

-- Antes da redução-$\eta$
sumList :: [Int] -> Int
sumList xs = foldr (+) 0 xs

-- Após a redução-$\eta$
sumList :: [Int] -> Int
sumList = foldr (+) 0

Este exemplo demonstra como a redução-$\eta$ pode simplificar a definição de uma função que usa aplicação parcial. Vamos detalhar o processo:

1. Antes da redução-$\eta$: temos sumList xs = foldr (+) 0 xs define uma função sumList que toma uma lista de inteiros xs como argumento. A função usa foldr (fold right) com o operador + e o valor inicial 0 para somar todos os elementos da lista.

2. Aplicando a redução-$\eta$: observamos que xs aparece como o último argumento tanto no lado esquerdo (sumList xs) quanto no lado direito (foldr (+) 0 xs) da equação. A redução-$\eta$ nos permite remover este argumento xs de ambos os lados.

3. Após a redução-$\eta$: sumList = foldr (+) 0 é a forma simplificada. Isso define sumList como a aplicação parcial de foldr com os argumentos (+) e 0.

No cálculo lambda, temos:

O argumento xs é removido, deixando a aplicação parcial de foldr.

Podemos ver, outra vez, como isso funciona em programação funcional: ambas as versões de sumList são funcionalmente idênticas. Para qualquer lista xs, tanto sumList xs quanto foldr (+) 0 xs produzirão o mesmo resultado. Como nos exemplos anteriores, a versão após a redução-$\eta$ expressa mais diretamente que sumList é uma especialização de foldr. Elimina a necessidade de mencionar explicitamente o argumento xs, focando na operação de soma em si.

Neste exemplo, foldr (+) 0 é uma função parcialmente aplicada. Ela espera receber uma lista como seu último argumento. O que demonstra como a redução-$\eta$ pode revelar e tirar proveito da aplicação parcial em Haskell. A redução-$\eta$ neste caso, além de simplificar a sintaxe, destaca o conceito de aplicação parcial em programação funcional. Ela mostra como sumList pode ser definida como uma especialização de foldr, pronta para ser aplicada a uma lista de inteiros.

Exemplo 5. Operadores Infixos

-- Antes da redução-$\eta$
divideBy :: Int -> Int -> Int
divideBy x\;y = x `div` y

-- Após a redução-$\eta$
divideBy :: Int -> Int -> Int
divideBy = div

Este exemplo demonstra como a redução-$\eta$ pode simplificar a definição de uma função que utiliza um operador infixo. Vamos detalhar o processo:

1. Antes da redução-$\eta$ temos: divideBy x\;y = x div y que define uma função que usa o operador infixo div para divisão inteira. O formato div é a notação infixa para a função div.

   Em Haskell, operadores infixos são funções que são normalmente usadas entre dois argumentos. Qualquer função de dois argumentos pode ser usada como um operador infixo colocando-a entre crases (`). Neste caso, x div y é equivalente a div x\;y.

2. Aplicando a redução-$\eta$ observamos que x e y aparecem na mesma ordem no lado esquerdo e direito da equação. Logo, a redução-$\eta$ nos permite remover ambos os argumentos.

3. Após a redução-$\eta$ temos: divideBy = div é a forma simplificada. Isso define divideBy como sendo exatamente a função div.

Se considerarmos o cálculo lambda teremos:

Cada passo remove um argumento, resultando na função div por si só. As expressões divideBy x\;y e div x\;y são funcionalmente idênticas para quaisquer x e y. A versão reduzida divideBy = div deixa claro que divideBy é exatamente a mesma função que div.

Observe que graças a redução-$\eta$ a definição se torna mais concisa e direta. Revelando que divideBy não adiciona nenhuma funcionalidade extra à div. Permitindo que divideBy seja usado tanto de forma infixa quanto prefixa, assim como div. Neste caso, a redução-$\eta$ mostra com um operador infixo pode ser simplificada para revelar sua equivalência direta com a função de divisão padrão. Isso ilustra a flexibilidade do Haskell em tratar operadores e funções intercambiavelmente.

3.3.5. 6. Funções Anônimas

-- Antes da redução-$\eta$
processList :: [Int] -> [Int]
processList = map (\x -> x * 2)

-- Após a redução-$\eta$
processList :: [Int] -> [Int]
processList = map (* 2)

Este exemplo demonstra como a redução-$\eta$ pode simplificar o uso de funções anônimas, conhecidas como lambdas em Haskell. Vamos detalhar o processo:

1. Antes da redução-$\eta$ temos: processList = map (\x -> x * 2) define uma função que aplica map a uma função anônima. Ou seja, a função anônima \x -> x * 2 multiplica cada elemento por 2.

2. Aplicando a redução-$\eta$: observamos que a função anônima \x -> x * 2 pode ser reescrita como uma aplicação parcial do operador *. (\x -> x * 2) é equivalente a (* 2).

Após a redução-$\eta$ temos: processList = map (* 2) é a forma simplificada. Nesta declaração, (* 2) é uma seção em Haskell, uma forma de aplicação parcial para operadores infixos.

No cálculo lambda temos:

Neste caso, o argumento x será removido, deixando a aplicação parcial do operador *.

No caso da programação funcional, as duas versões de processList são funcionalmente idênticas. Para qualquer lista de inteiros, tanto map (\x -> x * 2) quanto map (* 2) produzirão o mesmo resultado.

Observe que a versão após a redução-$\eta$ é mais concisa e expressiva. Eliminando a necessidade de criar uma função anônima explícita e, ao mesmo tempo, aproveitando a notação de seção do Haskell para operadores infixos.

Finalmente, talvez a amável leitora deva saber que uma seção é uma forma de aplicar parcialmente um operador infixo. Ou seja, (* 2) é equivalente a \x -> x * 2. Seções podem ser formadas com o operando à esquerda (2 *) ou à direita (* 2). Neste caso, a redução-$\eta$ simplifica a sintaxe e demonstra como aproveitar as características da linguagem Haskell, como operadores infixos e seções, para criar código mais conciso e expressivo.

3.3.6. A redução-$\eta$ e a Otimização de Compiladores

A redução-$\eta\,$, além de ser um conceito teórico do cálculo lambda e uma técnica de refatoração em programação funcional, tem implicações significativas na otimização de código por compiladores. Ela oferece várias oportunidades para melhorar a eficiência do código gerado, especialmente em linguagens funcionais.

Uma das principais aplicações da redução-$\eta$ na otimização é a eliminação de funções intermediárias desnecessárias. Por exemplo, uma função definida como f x\;y = g (h x) y pode ser otimizada para f = g . h. Esta simplificação reduz a criação de closures e o número de chamadas de função, resultando em código mais eficiente.

No contexto da otimização de compiladores e da redução-$\eta$, closures são estruturas de dados que combinam uma função com seu ambiente léxico. Elas surgem quando uma função captura variáveis do escopo externo, permitindo seu acesso mesmo após o fim do escopo original. Em linguagens funcionais, closures são usadas para implementar funções de ordem superior e currying. Do ponto de vista da otimização, a criação e manutenção de closures podem impactar o uso de memória e o desempenho. A redução-$\eta$ pode eliminar closures desnecessárias, como quando uma função apenas repassa argumentos para outra sem modificá-los. Nesse caso, o compilador pode substituir a closure intermediária por uma referência direta à função original, melhorando o uso de memória e o tempo de execução.

A redução-$\eta$ facilita o inlining de funções, uma técnica na qual o compilador substitui chamadas de função por seu corpo. Por exemplo, uma definição como map' f = map f pode levar o compilador a fazer inline de map', substituindo-a diretamente por map. Isso melhora o desempenho enquanto reduz a alocação de memória para closures, o que é particularmente benéfico em linguagens com coleta de lixo, garbage collector, como é o cado do Haskell.

Em linguagens que utilizam _currying_extensivamente, a redução-$\eta$ pode otimizar a aplicação parcial de funções. Uma expressão como addOne = (+) 1 pode ser otimizada para evitar a criação de uma closure intermediária, melhorando tanto o uso de memória quanto o desempenho.

A fusão de funções é outra área na qual a redução-$\eta$ pode ser útil. Ela pode facilitar a combinação de múltiplas funções em uma única passagem, como transformar sum . map (*2) em uma única função que multiplica e soma em uma operação. Isso reduz o overhead de iterações múltiplas sobre estruturas de dados.

A redução-$\eta$ simplifica a análise de fluxo de dados, permitindo que o compilador rastreie mais facilmente como os valores são usados e transformados. Isso pode levar a otimizações mais eficazes em nível de código de máquina. Em alguns casos, pode até transformar chamadas não-tail em chamadas tail, permitindo a otimização de tail call, crucial para linguagens que garantem essa otimização, como Scheme.

A simplificação da estrutura das funções através da redução-$\eta$ pode resultar em código de máquina mais eficiente e mais fácil de otimizar posteriormente. Isso pode ajudar na especialização de funções polimórficas, levando a implementações mais eficientes para tipos específicos.

No contexto de otimizações inter-procedurais, a redução-$\eta$ pode facilitar a análise e otimização de funções através de limites de módulos, permitindo otimizações mais abrangentes.

É importante notar que a aplicação dessas otimizações deve ser equilibrada com outros fatores, como tempo de compilação e tamanho do código gerado. Em alguns casos, a redução-$\eta$ pode interferir com outras otimizações ou com a legibilidade do código de depuração. Compiladores modernos para linguagens funcionais, como o GHC para Haskell, incorporam a redução-$\eta$ como parte de um conjunto mais amplo de técnicas de otimização.

Em suma, a redução-$\eta$ desempenha um papel importante na otimização de compiladores, especialmente para linguagens funcionais, contribuindo significativamente para a geração de código mais eficiente e performático.

3.4. Teorema de Church-Rosser

Um dos obstáculos enfrentado por Church durante o desenvolvimento do cálculo lambda dizia respeito a consistência do processo de redução. Ou seja, provar que um termo lambda mesmo que reduzido de formas diferentes, chegaria a mesma forma normal, caso esta forma existisse. Em busca desta consistência, Church e J. Barkley Rosser, seu estudante de doutorado, formularam o teorema que viria a ser chamado de Teorema de Church-Rosser⁸. Este teorema, chamado de propriedade da confluência local, garante a consistência e a previsibilidade do sistema de redução beta, afirmando que, independentemente da ordem em que as reduções beta são aplicadas, o resultado\;se existir, é o mesmo Figura 3.4.A.

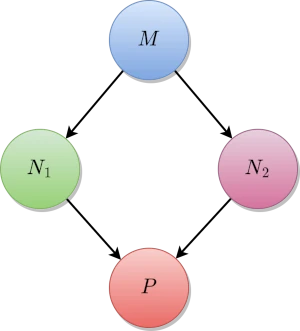
Figura 3.4.A: Diagrama da Propriedade de Confluência determinada pelo Teorema de Church-Rosser

Formalmente teremos:

Ou:

O símbolo $\twoheadrightarrow_\beta$ representa uma sequência, possivelmente vazia, de reduções beta. Com um pouco menos de formalidade, podemos ler o enunciado do Teorema de Church-Rosser como:

Se um termo $M$ pode ser reduzido a $N_1$ e $N_2$ exclusivamente em um passo, então existe um termo $P$ tal que $N_1$ e $N_2$ podem ser reduzidos a $P\,$.

A prova de Barendregt utiliza o Lema de Newman, que afirma que um sistema de reescrita é confluentemente terminante se for fortemente normalizante e localmente confluentemente terminante. A prova pode ser dividida em três partes principais:

1. Confluência Local: a confluência local é definida da seguinte forma:

Se $M$ é um termo no cálculo lambda e pode ser reduzido em um passo para dois termos distintos $N_1$ e $N_2\,$, então existe um termo comum $ P$ tal que $N_1$ e $N_2$ podem ser reduzidos em um número finito de passos para $P\,$. Formalmente:

\[M \rightarrow N_1 \quad \text{e} \quad M \rightarrow N_2 \implies \exists P \, : \, N_1 \twoheadrightarrow P \quad \text{e} \quad N_2 \twoheadrightarrow P\]

Por exemplo: considere o termo $ M = (\lambda x. x\;x) (\lambda x. x\;x)\,$. Esse termo pode ser reduzido de duas formas diferentes:

1. Redução da aplicação externa: $(\lambda x.\;x\;x) (\lambda x.\;x\;x) \rightarrow (\lambda x.\;x\;x) (\lambda x.\;x\;x)$ (permanece o mesmo)

2. Redução da aplicação interna: $(\lambda x.\;x\;x) (\lambda x.\;x\;x) \rightarrow (\lambda x.\;x\;x)$

   No entanto, ambos os caminhos eventualmente se reduzem ao mesmo termo $(\lambda x.\;x\;x)\,$, o que ilustra a confluência local.

3. Confluência Global: a confluência global é estabelecida ao aplicar o Lema de Newman, que afirma que:

   1. Se um sistema de reescrita é fortemente normalizante, ou seja, todas as sequências de reduções terminam em um termo normal, e

   2. Se o sistema é localmente confluentemente terminante, então ele é globalmente confluentemente terminante.

Para aplicar o Lema de Newman no cálculo lambda, é necessário provar duas coisas: a Normalização forte, todos os termos no cálculo lambda podem eventualmente ser reduzidos a uma forma normal (caso exista) e a Confluência local, que demonstrei anteriormente.

Como o cálculo lambda satisfaz ambas as condições, ele é confluente e terminante globalmente.

A prova completa envolve mostrar que, mesmo quando existem múltiplos >redexes, subtermos que podem ser reduzidos, a ordem de redução não interfere no resultado . Barendregt utiliza as técnicas de reescrita paralela e substituição simultânea para lidar com as reduções múltiplas.

A reescrita paralela envolve a ideia de aplicar todas as reduções possíveis de um termo ao mesmo tempo. Por exemplo, se um termo $M$ contém dois redexes diferentes, como $(\lambda x.\;x)\;(\lambda y.\;y)\,$, a reescrita paralela reduz ambos os redexes simultaneamente:

\[M = (\lambda x.\;x)\;(\lambda y.\;y) \rightarrow (\lambda y.\;y)\]

Essa abordagem simplifica a prova de confluência, pois elimina a necessidade de considerar todas as possíveis sequências de redução.

Já substituição simultânea é usada para manter a consistência ao aplicar várias reduções ao mesmo tempo. Por exemplo, se temos um termo $(\lambda x.\;M)\;N\,$, a substituição simultânea permite que o termo $M[N/x]$ seja avaliado sem considerar ordens de substituição diferentes.

A prova de confluência de Barendregt é considerada elegante devido à sua simplicidade e clareza ao estruturar a demonstração de confluência no cálculo lambda. Notadamente porque: assegura a consistência do cálculo lambda, permite que linguagens de programação baseadas no cálculo lambda sejam previsíveis e determinísticas e tem implicações diretas na teoria da prova, nas linguagens de programação funcional e na lógica computacional. ⁹

O Teorema de Church-Rosser ao estabelecer que o cálculo lambda é um sistema confluente, estabelece que, embora possam existir diferentes caminhos de redução a partir de um termo inicial, todos os caminhos levam a um resultado comum. além de provar a consistência do cálculo lambda, O Teorema de Church-Rosser teve impacto na prova da existência da unicidade da forma normal e da independência da estratégia de redução.

Finalmente podemos dizer que o cálculo lambda puro é consistente porque como não é possível derivar termos contraditórios, ou ambíguos. A consistência, por sua vez, implica na confiabilidade em sistemas formais e linguagens de programação funcionais.

Por sua vez, a Unicidade da Forma Normal é uma consequência imediata da consistência. Se um termo $M$ possui uma forma normal, um termo irredutível, então essa forma normal é única. Isso assegura que o processo de computação no cálculo lambda é determinístico em termos do resultado . Até aqui, vimos que o cálculo lambda é consistente e determinístico.

A última consequência do Teorema de Church-Rosser, a Independência da Estratégia de Redução garante que a ordem, ou estratégia, com que as reduções beta são aplicadas não afeta a forma normal final de um termo. Isso permite flexibilidade na implementação de estratégias de avaliação, como avaliação preguiçosa (lazy evaluation) ou avaliação estrita (eager evaluation).

Finalmente, podemos dizer que o Teorema de Church-Rosser é o suporte necessário para que a amável leitora possa entender que o cálculo lambda é consistente, determinístico e flexível. A esforçada leitora de acompanhar os seguintes exemplos:

Exemplo 1: redução de uma Função Aplicada a Dois Argumentos. Considere o termo:

Caminho 1: reduza o termo externo primeiro:

Agora, aplique a segunda função:

Caminho 2: reduza o termo interno primeiro:

Reduza o termo externo:

Finalmente, aplique a segunda função:

Neste exemplo, ambos os caminhos de redução resultam na forma normal $5\,$.

Exemplo 2: redução de uma Função de Ordem Superior. Considere o termo:

Caminho 1: reduza o termo externo primeiro:

Aplique a função interna:

Aplique a primeira função:

Aplique a segunda função:

Caminho 2: reduza o termo interno primeiro:

Aplique a função externa:

Agora, aplique a função interna:

Aplique a primeira função:

Aplique a segunda função:

Neste exemplo, ambos os caminhos de redução resultam na forma normal $3\,$.

Exemplo 3: considere o termo lambda:

Este termo pode ser reduzido de formas diferentes:

Caminho 1: reduza o termo externo primeiro:

Se tomarmos o caminho 1, este processo continuará indefinidamente, indicando que não há forma normal.

Caminho 2: reduza o termo interno primeiro:

Novamente, o processo é infinito e não temos uma forma normal.

Neste caso, ambos os caminhos levam a um processo de redução infinito, mas o Teorema de Church-Rosser assegura que, se houvesse uma forma normal, ela seria única, independentemente do caminho escolhido.

A confluência garantida pelo Teorema de Church-Rosser é análoga a um rio com vários afluentes que eventualmente convergem para o mesmo oceano. Ou se preferir a antiga expressão latina Omnes viae Romam ducunt Não importa qual caminho a água siga, ou que estrada a nômade leitora pegue, ela acabará chegando ao mesmo destino. No contexto do cálculo lambda, isso significa que diferentes sequências de reduções beta não causam ambiguidades no resultado da computação.

Questão de prova: o teorema de Church-Rosser indica que se um termo pode ser reduzido de duas formas diferentes, então existe uma forma comum que ambas as reduções eventualmente alcançarão. Prove que o termo, M, a seguir satisfaz o teorema de Church-Rosser $M = (\lambda f. \; f\; (f\; 3)) (\lambda x. \; x + 1)$.

Podemos considerar duas ordens principais de redução:

1. Redução Externa Primeiro: nesta abordagem, primeiro aplicamos a função externa ao argumento. Depois, resolvemos qualquer aplicação interna que surgir.

• Primeiro, aplicamos $(\lambda f. \;f\;(f\;3))$ ao argumento $(\lambda x.\;x + 1)$. Isso significa substituir $f$ por $(\lambda x.\;x + 1)$:

\[M = (\lambda x.\;x + 1)\;((\lambda x.\;x + 1)\;3)\]

• Agora, resolvemos a aplicação interna $(\lambda x.\;x + 1)\;3$:

\[(\lambda x.\;x + 1)\;3 = 4\]

• Finalmente, aplicamos $(\lambda x.\;x + 1)$ ao valor $4$:

\[M = (\lambda x.\;x + 1)\;4 = 5\]

1. Redução de Cabeça (Redução Interna Primeiro): nesta abordagem, reduzimos primeiro os termos internos antes de aplicar a função externa ao argumento.

• Neste caso, resolvemos a expressão interna antes de aplicar a função externa. Portanto, começamos pela parte mais interna, que é $(f\;3)$ em $(\lambda f.\;f\;(f\;3))$.

• Primeiro, aplicamos $(\lambda f.\;f\;(f\;3))$ ao argumento $(\lambda x.\;x + 1)$:

\[M = (\lambda x.\;x + 1)\;((\lambda x.\;x + 1)\;3)\]

• Resolva a aplicação interna $(\lambda x.\;x + 1)\;3$:

\[(\lambda x.\;x + 1)\;3 = 4\]

• Finalmente, aplique $(\lambda x.\;x + 1)$ ao valor $4$:

\[M = (\lambda x.\;x + 1)\;4 = 5\]

O Teorema de Church-Rosser fornece uma base teórica para otimizações de compiladores e interpretadores, garantindo que mudanças na ordem de avaliação não alterem o resultado . Tem impacto na teoria da computação já que a confluência é uma propriedade desejável em sistemas de reescrita de termos, assegurando a consistência lógica e a previsibilidade dos sistemas formais. Em sistemas de provas formais e lógica matemática o Teorema de Church-Rosser ajuda a garantir que as demonstrações não levem a contradições.

3.5. Currying

O cálculo Lambda assume intrinsecamente que uma função possui um único argumento. Esta é a ideia por trás da aplicação. Como a atenta leitora deve lembrar: dado um termo $M$ visto como uma função e um argumento $N\,$, o termo $(M\;N)$ representa o resultado de aplicar $M$ ao argumento $N\,$. A avaliação é realizada pela redução-$\beta\,$.

Embora o cálculo lambda defina funções unárias estritamente, aqui, não nos limitaremos a essa regra para facilitar o entendimento dos conceitos de substituição e aplicação.

O conceito de _currying_vem do trabalho do matemático Moses Schönfinkel, que iniciou o estudo da lógica combinatória nos anos 1920. Mais tarde, Haskell Curry popularizou e expandiu essas ideias. O cálculo lambda foi amplamente influenciado por esses estudos, tornando o _currying_uma parte essencial da programação funcional e da teoria dos tipos.

Por exemplo, uma função de dois argumentos $f(x, y)$ pode ser convertida em uma sequência de funções $f’(x)(y)\,$. Aqui, $f’(x)$ retorna uma nova função que aceita $y$ como argumento. Assim, uma função que requer múltiplos parâmetros pode ser aplicada parcialmente, fornecendo alguns argumentos de cada vez, resultando em uma nova função que espera os argumentos restantes. Ou, com um pouco mais de formalidade: uma função de $n$ argumentos é vista como uma função de um argumento que toma uma função de $n - 1$ argumentos como argumento.

Considere uma função $f$ que aceita dois argumentos: $f(x, y)$ a versão currificada desta função será:

Agora, $F$ é uma função que aceita um argumento $x$ e retorna outra função que aceita $y\,$. Podemos ver isso com um exemplo: suponha que temos uma função que soma dois números: $soma(x, y) = x + y\,$. A versão currificada seria:

Isso significa que $add$ é uma função que recebe um argumento $x$ e retorna outra função $\lambda y.(\;x + y)\,$. Esta função resultante espera um segundo argumento $y$ para calcular a soma de $x$ e $y\,$.

Quando aplicamos $add$ ao argumento $3\,$, obteremos:

Nesse ponto, estamos substituindo $x$ por $3$ na função externa, resultando em:

Isso é uma nova função que espera um segundo argumento $y\,$. Agora, aplicamos o segundo argumento, $4\,$, à função resultante:

Substituímos $y$ por $4\,$, obtendo:

Finalmente:

Assim, $(add \;3) \;4$ é avaliado para $7$ após a aplicação sequencial de argumentos à função currificada. A Figura 3.5.A, apresenta a aplicação $(add \; 3) = (\lambda x.\;(\lambda y.\;(x + y))) \; 3$ que explicamos acima.

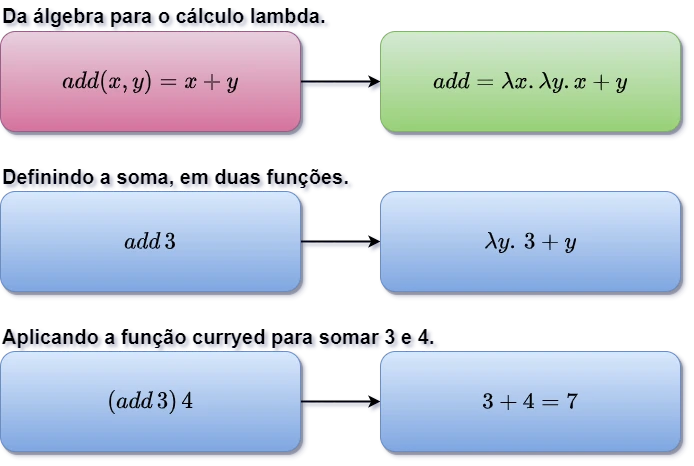_Figura 3.5.A: Diagrama mostrando o processo de currying_em Cálculo lambda

No currying, uma função que originalmente recebe dois argumentos, como $f: \mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}\,$, é transformada em uma função que recebe um argumento e retorna outra função. O resultado é uma função da forma $f’: \mathbb{N} \rightarrow (\mathbb{N} \rightarrow \mathbb{N})\,$. Assim, $f’$ recebe o primeiro argumento e retorna uma nova função que espera o segundo argumento para realizar o cálculo final.

Podemos representar essa transformação de forma mais abstrata usando a notação da teoria dos conjuntos. Uma função que recebe dois argumentos é representada como $\mathbb{N}^{\mathbb{N} \times \mathbb{N}}\,$, o que significa “o conjunto de todas as funções que mapeiam pares de números naturais para números naturais”. Quando fazemos currying, essa função é transformada em $(\mathbb{N}^{\mathbb{N}})^{\mathbb{N}}\,$, o que significa “o conjunto de todas as funções que mapeiam um número natural para outra função que, por sua vez, mapeia um número natural para outro”. Assim, temos uma cadeia de funções aninhadas.

Podemos fazer uma analogia com a álgebra:

Aqui, elevar uma potência a outra potência equivale a multiplicar os expoentes. Similarmente, no currying, estruturamos as funções de forma aninhada, mas o resultado é equivalente, independentemente de aplicarmos todos os argumentos de uma vez ou um por um. Portanto, o currying cria um isomorfismo entre as funções dos tipos:

e

Este isomorfismo significa que as duas formas são estruturalmente equivalentes e podem ser convertidas uma na outra sem perda de informação ou alteração do comportamento da função. A função $f$ que recebe um par de argumentos $(a, b)$ é equivalente à função $g$ que, ao receber $a\,$, retorna uma nova função que espera $b\,$, permitindo que os argumentos sejam aplicados um por vez.

Podemos entender melhor o conceito de _currying_dentro de um contexto mais abstrato, o da teoria das categorias. A teoria das categorias é uma área da matemática que busca generalizar e estudar relações entre diferentes estruturas matemáticas através de objetos e mapeamentos entre eles, chamados de morfismos. No caso do currying, ele se encaixa no conceito de uma categoria fechada cartesiana (CCC). Uma CCC é uma categoria que possui certas propriedades que tornam possível a definição e manipulação de funções de forma abstrata, incluindo a existência de produtos, como pares ordenados de elementos, e exponenciais, que são equivalentes ao conjunto de todas as funções entre dois objetos.

No contexto do currying, uma CCC permite que funções multivariadas sejam representadas similarmente as funções que aceitam um argumento por vez. Por exemplo, quando representamos uma função como $f: A \times B \to C\,$, estamos dizendo que $f$ aceita um par de argumentos e retorna um valor. Com currying, essa função pode ser reestruturada como $g: A \to (B \to C)\,$, na qual $g$ aceita um argumento $a\,$, e retorna uma nova função que aceita um argumento $b$ para então retornar o valor final. Esse tipo de reestruturação só é possível porque as operações básicas de uma CCC, como produto e exponenciais, garantem que esse tipo de transformação é sempre viável e consistente. Assim, a noção de categoria fechada cartesiana formaliza a ideia de que funções podem ser aplicadas um argumento de cada vez, sem perder a equivalência com uma aplicação de múltiplos argumentos simultâneos.

Essa estrutura abstrata da teoria das categorias ajuda a explicar por que o _currying_é uma ferramenta tão natural no cálculo lambda e na programação funcional. No cálculo lambda, todas as funções são unárias por definição; qualquer função que precise de múltiplos argumentos é, na verdade, uma cadeia de funções unárias que se encaixam umas nas outras. Esse comportamento é um reflexo direto das propriedades de uma categoria fechada cartesiana. Cada vez que transformamos uma função multivariada em uma sequência de funções aninhadas, estamos explorando a propriedade exponencial dessa categoria, que se comporta de forma semelhante à exponenciação que conhecemos na álgebra. A identidade $(m^n)^p = m^{n \cdot p}$ é um exemplo de como uma estrutura aninhada pode ser vista de forma equivalente a uma única operação combinada.

Entender o _currying_como uma parte de uma categoria fechada cartesiana nos permite uma visão mais profunda sobre como a programação funcional e o cálculo lambda operam. O _currying_não é simplesmente uma técnica prática para simplificar a aplicação de funções; é, na verdade, uma manifestação de uma estrutura matemática mais ampla, que envolve composição, abstração e a criação de novas funções a partir de funções existentes. Essa perspectiva ajuda a conectar o ato prático de currificar funções com a teoria abstrata que fundamenta essas operações, revelando a elegância que há na reestruturação de funções e na capacidade de manipular argumentos um por um.

Voltando ao cálculo lambda, a atenta leitora deve lembrar que todas as funções são unárias, por definição. Assim, funções que parecem aceitar múltiplos argumentos são, na verdade, uma cadeia de funções que retornam outras funções. Vamos ilustrar isso com um exemplo usando a concatenação de strings.

Para começar, vamos definir uma função que concatena duas strings:

Aqui, $\lambda s_1$ cria uma função que recebe a primeira string $s_1$ e retorna outra função $\lambda s_2\,$, que então recebe a segunda string $s_2$ e realiza a concatenação. Quando aplicamos o primeiro argumento, obtemos:

Agora, podemos aplicar o segundo argumento:

Outro exemplo seria uma função que cria uma saudação personalizada. Primeiro, vamos definir a função currificada:

Aplicando o primeiro argumento:

E, em seguida, aplicando o segundo argumento:

Esses exemplos mostram como o _currying_facilita a aplicação parcial de funções, especialmente em contextos nos quais queremos criar funções específicas a partir de funções mais gerais, aplicando somente alguns dos, ou um argumento inicialmente. Obtendo mais flexibilidade e modularidade no desenvolvimento de nossas funções.

3.5.1. _currying_em Haskell

Haskell implementa o _currying_por padrão para todas as funções. Isso significa que cada função em Haskell tecnicamente aceita somente um argumento, mas pode ser aplicada parcialmente para criar novas funções. Podemos definir uma função de múltiplos argumentos assim:

add :: Int -> Int -> Int
add x y = x + y

Essa definição é equivalente a:

add :: Int -> (Int -> Int)
add = \x -> (\y -> x + y)

Aqui, add é uma função que aceita um Int e retorna uma função que aceita outro Int e retorna a soma.

A aplicação parcial é trivial em Haskell. Sempre podemos criar novas funções simplesmente não fornecendo todos os argumentos:

addCinco :: Int -> Int
addCinco = add 5

resultado :: Int
resultado = addCinco 3  -- Retorna 8

Além da definição de funções usando _currying_e da aplicação parcial. O uso do _currying_no Haskell torna as funções de ordem superior naturais em Haskell:

aplicaDuasVezes :: (a -> a) -> a -> a
aplicaDuasVezes f x = f (f x)

incrementaDuasVezes :: Int -> Int
incrementaDuasVezes = aplicaDuasVezes (+1)

resultado :: Int
resultado = incrementaDuasVezes 5  -- Retorna 7

Operadores infixos são funções binárias (que aceitam dois argumentos) escritas entre seus operandos. Por exemplo, +, -, *, / são operadores infixos comuns. Em Haskell, operadores infixos podem ser facilmente convertidos em funções currificadas usando seções.

Seções são uma característica do Haskell que permite a aplicação parcial de operadores infixos. Elas são uma forma concisa de criar funções anônimas a partir de operadores binários.

1. Definição: Uma seção é criada ao colocar um operador infixo e um de seus operandos entre parênteses. Isso cria uma função que espera o operando faltante.

dobra :: Int -> Int
dobra = (*2)

metade :: Float -> Float
metade = (/2)

Finalmente em Haskell o uso do _currying_permite escrever código mais conciso e expressivo. Enquanto facilita a criação de funções especializadas a partir de funções mais gerais e torna a composição de funções mais natural e intuitiva.

3.5.3. Ordem Normal e Estratégias de Avaliação

A ordem em que as reduções beta são aplicadas pode afetar tanto a eficiência quanto a terminação do cálculo. Existem duas principais estratégias de avaliação:

1. Ordem Normal: Sempre reduz o redex mais externo à esquerda primeiro. Essa estratégia garante encontrar a forma normal de um termo, se ela existir. Na ordem normal, aplicamos a função antes de avaliar seus argumentos.

2. Ordem Aplicativa: Nesta estratégia, os argumentos são reduzidos antes da aplicação da função. Embora mais eficiente em alguns casos, pode não terminar em expressões que a ordem normal resolveria.

A Figura 3.5.3.A apresenta um diagrama destas duas estratégias de avaliação.

Figura 3.5.3.A: Diagrama de Aplicação nas Ordens Normal e Aplicativa.{: class=”legend”}

Talvez a atenta leitora entenda melhor vendo as reduções sendo aplicadas:

1. Ordem Normal: A função $(\lambda x.\;y)$ é aplicada diretamente ao argumento $(\lambda z.\;z\;z)\,$, resultando em:

   \[(\lambda x.\;y)(\lambda z.\;z\;z) \to_\beta y\]

Aqui, não precisamos avaliar o argumento, pois a função simplesmente retorna $y\,$.

1. Ordem Aplicativa: Primeiro, tentamos reduzir o argumento $(\lambda z.\;z\;z)\,$, resultando em uma expressão que se auto-aplica indefinidamente, causando um loop infinito:

   \[(\lambda x.\;y)(\lambda z.\;z\;z) \to_\beta (\lambda x.\;y)((\lambda z.\;z\;z)(\lambda z.\;z\;z)) \to_\beta ...\]

Este exemplo mostra que a ordem aplicativa pode levar a uma não terminação em termos nos quais a ordem normal poderá encontrar uma solução.

3.6. Combinadores e Funções Anônimas

Os combinadores tem origem no trabalho de Moses Schönfinkel. Em um artigo de 1924 Moses Schönfinkel define uma família de combinadores incluindo os combinadores padrão $S\,$, $K$ e $I$ e demonstra que apenas $S$ e $K$ são necessários[\^cite3]. Um conjunto dos combinadores iniciais pode ser visto na Tabela 3.6.A:

Tabela 3.6.A: Relação dos Combinadores Originais.

A Figura 3.6.A mostra as definições dos combinadores $I\,$, $K\,$, $S\,$, e uma aplicação de exemplo de cada um.

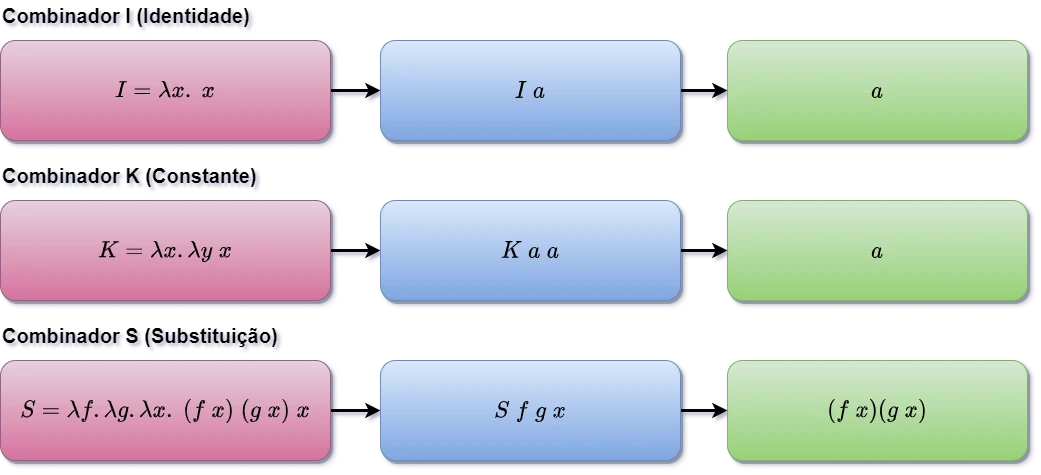Figura 3.6.A: Definição e Aplicação dos Combinadores $I\,$, $K\,$, $S${: class=”legend”}

Schönfinkel apresentou combinadores para representar as operações da lógica de primeiro grau, um para o traço de Sheffer, NAND, descoberto em 1913, e outro para a quantificação.

Em funções booleanas e no cálculo proposicional, o traço de Sheffer é uma operação lógica que representa a negação da conjunção. Essa operação é expressa em linguagem comum como não ambos. Ou seja, dados dois operandos, ao menos um deles deve ser falso. Em termos técnicos, essa operação é chamada de não-conjunção, negação alternativa ou NAND, dependendo do texto no qual estão sendo analisados. Esta operação simplesmente nega a conjunção dos operandos e esta é a origem da nomenclatura NAND a abreviação de Not AND.

Esta operação foi introduzida pelo filósofo e lógico Henry Maurice Sheffer, por isso o nome, em 1913.

O trabalho que definiu o traço de Sheffer demonstrou que todas as operações booleanas podem ser expressas usando somente a operação NAND, simplificando a lógica proposicional. Em lógica de primeira ordem representamos esta a operação NAND por $ \mid \,$, $\uparrow\,$, ou $\overline{\wedge}\,$. Não é raro que neófitos confundam a representação do traço de Sheffer com $\vert \vert\,$, que normalmente é usado para representar disjunção. A precavida leitora deve tomar cuidado com isso.

Formalmente, a operação $p \mid q$ pode ser expressa como:

\[p \mid q = \neg (p \land q)\]

Indicando que a operação do Traço de Sheffer é verdadeira quando a proposição $p \land q$ é falsa. Quando não ambos $p$ e $q$ são verdadeiros.

O Traço de Sheffer possuí as seguintes propriedades:

1. Universalidade: a operação NAND é uma operação lógica universal, significando que qualquer função booleana pode ser construída apenas com NANDs. Isso é particularmente importante em eletrônica digital. A popularidade dessa porta em circuitos digitais se deve à sua versatilidade e à sua implementação relativamente simples em termos de hardware.

2. Identidade: O traço de Sheffer é auto-dual e pode representar qualquer outra operação lógica. Podemos representar a disjunção, a conjunção, a negação, o condicional ou a bicondicional através de combinações específicas de NANDs.

A importância da NAND pode ser verificada construindo uma operação de negação ($\neg p$) usando o traço de Sheffer, podemos fazê-lo com a seguinte expressão:

\[\neg p = p \mid p\]

Neste caso, $p \mid p$ significa “não ambos $p$ e $p$”, ou seja, simplesmente $\neg p\,$.

$p$	$p \mid p$	$\neg p$
V	F	F
F	V	V

Quando $p$ é verdadeiro ($V$): $p \mid p$ é falso, pois o operador NAND aplicado a dois valores verdadeiros resulta em falso. Portanto, $\neg p$ é falso. Quando $p$ é falso ($F$): $p \mid p$ é verdadeiro, pois o operador NAND aplicado a dois valores falsos resulta em verdadeiro. Portanto, $\neg p$ é verdadeiro.

Este exemplo simples ilustra como a operação NAND pode ser usada como um bloco de construção para criar outras operações lógicas.

Schönfinkel, inspirado em Sheffer, buscou reduzir a lógica de predicados ao menor número possível de elementos, e, anos mais tarde, descobriu-se que os quantificadores para todo e existe da lógica de predicados se comportam como abstrações lambda.

O que Schönfinkel e seus sucessores descobriram é que os quantificadores universais ($\forall$) e existenciais ($\exists$) podem ser modelados como abstrações lambda. A estrutura da lógica de predicados é compatível com as regras de abstração e aplicação do cálculo lambda.

O quantificador universal $\forall x. P(x)$ pode ser interpretado como uma função que, dada uma variável $x\,$, retorna verdadeiro para todos os valores de $x$ que satisfazem $P(x)\,$. Esta interpretação esta alinhada com o conceito de abstração lambda, na qual uma função recebe um argumento e retorna um valor dependendo desse argumento. Em termos de cálculo lambda, poderíamos expressar o quantificador universal:

\[\forall x. P(x) \equiv (\lambda x. P(x))\]

Aqui, a função $\lambda x. P(x)$ é uma abstração que, para cada $x\,$, verifica a verdade de $P(x)\,$.

Da mesma forma, o quantificador existencial $\exists x. P(x)$ pode ser interpretado como a aplicação de uma função que verifica se existe algum valor de $x$ que torna $P(x)$ verdadeiro. Novamente, isso pode ser modelado como uma abstração lambda:

\[\exists x. P(x) = (\lambda x. \neg P(x))\]

Essa correspondência revela a natureza fundamental das abstrações lambda e sua aplicação além do cálculo lambda puro.

Para nós, neste momento, um combinador é uma expressão lambda fechada, ou seja, sem variáveis livres. Isso significa que todas as variáveis usadas no combinador estão ligadas dentro da própria expressão.

A perceptiva leitora deve observar que o poder dos combinadores surge de que eles permitem criar funções complexas usando blocos simples, sem a necessidade de referenciar variáveis externas aos blocos.

Começamos com o combinador $K\,$, definido como:

Este combinador é uma função de duas variáveis que sempre retorna o primeiro argumento, ignorando o segundo. Ele representa o conceito de uma função constante. As funções constante sempre retornam o mesmo valor. No cálculo lambda o combinador $K$ sempre retorna o primeiro argumento independentemente do segundo.

Por exemplo, $KAB$ reduz para $A\,$, sem considerar o valor de $B$:

Os três combinadores, a seguir, são referenciados como básicos e estruturais para a definição de funções compostas em cálculo lambda:

1.Combinador I (Identidade):

O combinador identidade retorna o valor que recebe como argumento, sem modificá-lo.

Exemplo: aplicando o combinador $I$ a qualquer valor, ele retornará esse mesmo valor:

Outro exemplo:

2.Combinador K (ou C de Constante):

Este combinador ignora o segundo argumento e retorna o primeiro.

Exemplo: Usando o combinador $K$ com dois valores:

Aqui, o valor $7$ é retornado, e o valor $4$ ignorando.

3.Combinador S (Substituição):

Este combinador é mais complexo, pois aplica a função $f$ ao argumento $x$ e, simultaneamente, aplica a função $g$ a $x\,$, passando o resultado de $g(x)$ como argumento para $f\,$.

Exemplo: Vamos aplicar o combinador $S$ com as funções $f = \lambda z.\;z^2$ e $g = \lambda z.\;z + 1\,$, e o valor $3$:

Primeiro, substituímos $f$ e $g$:

Agora, aplicamos as funções:

Assim, $S\;(\lambda z.\;z^2)\;(\lambda z.\;z + 1)\;3$ resulta em $9\,$.

Finalmente, a lista de combinadores do cálculo lambda é um pouco mais extensa ¹⁰:

Tabela 3.6.B: Definições e Observações sobre os Combinadores.

No cálculo lambda as funções são anônimas. Desta forma, sempre é possível construir funções sem a atribuição nomes explícitos. Aqui estamos próximos da álgebra e longe das linguagens de programação imperativas, baseadas na Máquina de Turing. Isso é possível, como a atenta leitora deve lembrar, graças a existência das abstrações lambda:

A abstração lambda acima, representa uma função que aplica a função identidade ao seu argumento $x\,$. Nesse caso, a função interna $\lambda y.\;y$ é aplicada ao argumento $x\,$, e o valor resultante é simplesmente $x\,$, já que a função interna é a identidade. Estas funções inspiraram a criação de funções anônimas e alguns operadores em linguagens de programação imperativas. Como as funções arrow em JavaScript ou às funções lambdas em C++ e Python.

Os combinadores ampliam a utilidade das funções lambda e permitem a criação de funções complexas sem o uso de variáveis nomeadas. Esse processo, conhecido como abstração combinatória, elimina a necessidade de variáveis explícitas, focando em operações com funções. Podemos ver um exemplo de combinador de composição, denotado como $B\,$, definido por:

Aqui, $B$ aplica a função $f$ ao resultado da função $g\,$, ambas aplicadas a $x\,$. Esse é um exemplo clássico de um combinador que não utiliza variáveis explícitas e demonstra o poder do cálculo lambda puro, no qual toda computação pode ser descrita através de combinações.

Podemos ver um outro exemplo na construção do combinador Mockingbird, ou $M\,$. Um combinador que aplica uma função a si mesma, definido por:

Sua função é replicar a aplicação de uma função sobre si mesma, o que é fundamental em certas construções dentro do cálculo lambda, mas não se relaciona com o comportamento do combinador de composição.

Mesmo correndo o risco de ser redundante e óbvio, é preciso destacar que combinadores podem ser combinados. A expressão $S\;(K\;S)\;K$ é uma combinação de combinadores que possui um comportamento interessante. Podemos a analisar a estrutura do termo $S\;(K\;S)\;K$ observando que: o combinador $S$ é definido como $S = \lambda f.\lambda g.\lambda x.\;f\;x\;(g\;x)\,$, que aplica a função $f$ ao argumento $x\,$, e depois aplica $g$ ao mesmo argumento $x\,$, combinando os resultados; e o combinador $K$ é definido como $K = \lambda x.\lambda y.\;x\,$, que retorna sempre o primeiro argumento, ignorando o segundo. Voltando ao termo original:

A amável leitora deve ficar atenta a redução:

1. Primeiro, aplicamos $S$ ao primeiro argumento $(K\;S)$ e ao segundo argumento $K$:

   \[S(KS)K \rightarrow \lambda x.\;(K\;S)\;x (K\;x)\]

2. O termo $(KS)$ é aplicado a $x\,$, o que nos dará:

   \[(KS) x = (\lambda y.\;S)\;x = S\]

3. Agora, temos:

   \[S(KS)K \rightarrow \lambda x.\;S\;(K\;x)\]

Neste ponto, o combinador $S$ permanece, e o segundo termo $K\;x$ simplesmente retorna a constante $K\,$. O que resulta dessa combinação é uma forma que pode ser usada em certos contextos nos quais se deseja replicar parte do comportamento de duplicação de funções, similar ao combinador Mockingbird, mas com características próprias.

A capacidade de expressar qualquer função computável usando somente combinadores é formalizada pelo teorema da completude combinatória. Este teorema afirma que qualquer expressão lambda pode ser transformada em uma expressão equivalente utilizando os combinadores $S$ e $K$.

Exemplo 1: Definindo uma função constante com o combinador $K$

O combinador $K$ pode ser usado para criar uma função constante. A função criada sempre retorna o primeiro argumento, independentemente do segundo.

Definimos a função constante:

Quando aplicamos $f$ a qualquer valor, o resultado é sempre $A\,$, pois o segundo argumento é ignorado.

Exemplo 2: Definindo a aplicação de uma função com o combinador $S$

O combinador $S$ permite aplicar uma função a dois argumentos e combiná-los. Ele pode ser usado para definir uma função que aplica duas funções diferentes ao mesmo argumento e, em seguida, combina os resultados.

Definimos a função composta:

Aqui, $g$ e $h$ são duas funções que recebem o mesmo argumento $x\,$. O resultado é a combinação das duas funções aplicadas ao mesmo argumento.

A remoção de variáveis nomeadas simplifica a computação. Este é um dos pontos centrais da teoria dos combinadores.

Em linguagens funcionais como Haskell, essa característica é usada para criar expressões modulares e compostas. Isso traz clareza e concisão ao código.

3.7. Estratégias de Avaliação no Cálculo Lambda

As estratégias de avaliação determinam como expressões são computadas. Essas estratégias de avaliação terão impacto na implementação de linguagens de programação. Diferentes abordagens para a avaliação de argumentos e funções podem resultar em diferentes características de desempenho.

3.7.1. Avaliação por Valor vs Avaliação por Nome

No contexto do cálculo lambda e linguagens de programação, existem duas principais abordagens para avaliar expressões:

1. Avaliação por Valor: Nesta estratégia, os argumentos são avaliados antes de serem passados para uma função. O cálculo é feito de forma estrita, ou seja, os argumentos são avaliados imediatamente. Isso corresponde à ordem aplicativa de redução, a função é aplicada após a avaliação completa de seus argumentos. A vantagem desta estratégia é que ela pode ser mais eficiente em alguns contextos, pois o argumento é avaliado somente uma vez.

   Exemplo: Considere a expressão $(\lambda x.\;x + 1) (2 + 3)\,$.

   Na avaliação por valor, primeiro o argumento $2 + 3$ é avaliado para $5\,$, e em seguida a função é aplicada:

   \[(\lambda x.\;x + 1)\;5 \rightarrow 5 + 1 \rightarrow 6\]

2. Avaliação por Nome: Argumentos são passados para a função sem serem avaliados imediatamente. A avaliação ocorre quando o argumento é necessário. Esta estratégia corresponde à ordem normal de redução, em que a função é aplicada diretamente e o argumento só é avaliado quando estritamente necessário. Uma vantagem desta abordagem é que ela pode evitar avaliações desnecessárias, especialmente em contextos nos quais certos argumentos nunca são utilizados.

   Exemplo: Usando a mesma expressão $\lambda x.\;x + 1) (2 + 3)\,$, com avaliação por nome, a função seria aplicada sem avaliar o argumento de imediato:

   \[(\lambda x.\;x + 1) (2 + 3) \rightarrow (2 + 3) + 1 \rightarrow 5 + 1 \rightarrow 6\]

4. Estratégias de Redução

No cálculo lambda, a ordem em que as expressões são avaliadas define o processo de redução dos termos. As duas estratégias mais comuns para essa avaliação são a _estratégia normal e a estratégia aplicativa.

Na estratégia normal, as expressões mais externas são reduzidas antes das internas. Já na estratégia aplicativa, os argumentos de uma função são reduzidos primeiro, antes de aplicar a função.

Essas estratégias influenciam o resultado e o comportamento do processo de computação, especialmente em expressões que podem divergir ou não possuir valor definido. Vamos ver estas estratégias com atenção.

4.1. Ordem Normal (Normal-Order)

Na ordem normal, a redução prioriza o redex mais externo à esquerda (redução externa). Essa estratégia é garantida para encontrar a forma normal de um termo, caso ela exista. Como o argumento não é avaliado de imediato, é possível evitar o cálculo de argumentos que nunca serão utilizados, tornando-a equivalente à avaliação preguiçosa em linguagens de programação.

Uma vantagem da ordem normal é que sempre que encontramos a forma normal de um termo, se existir, podemos evitar a avaliação de argumentos desnecessários. Melhorando a eficiência do processo em termos de espaço.

Por outro lado, a ordem normal pode ser ineficiente em termos de tempo, já que, acabamos por reavaliar expressões várias vezes quando elas são necessárias repetidamente.

Exemplo 1: considere a expressão:

Na ordem normal, a redução ocorre:

O argumento $((\lambda z.\;z\;z) (\lambda w. w w))$ não é avaliado, pois ele nunca é utilizado no corpo da função.

Exemplo 2: Considere a expressão:

Vamos reduzir $M$ usando a ordem normal.

Passo 1: Identificamos o redex mais externo à esquerda:

Aplicamos a redução beta ao redex, substituindo $f$ por $(\lambda y.\;y + 1)$:

Passo 2: Novamente, identificamos o redex mais externo à esquerda:

Aplicamos a redução beta, substituindo $x$ por $(\lambda x.\;(\lambda y.\;y + 1)\;(x\;x))$:

Passo 3: Dentro do argumento, identificamos o redex mais externo:

Aplicamos a redução beta novamente, substituindo $x$ por $(\lambda x.\;(\lambda y.\;y + 1)\;(x\;x))$:

Passo 4: Observamos que o processo está se repetindo. A cada aplicação da redução beta, o termo dentro dos parênteses permanece o mesmo, indicando um loop infinito:

Na estratégia de ordem normal, a redução do termo $M$ não termina, pois entra em um ciclo infinito de reduções. Não é possível alcançar uma forma normal para $M$ usando esta estratégia, já que continuaremos expandindo o termo indefinidamente sem simplificá-lo a um resultado . Este exemplo ilustra como a ordem normal pode levar a reduções infinitas em certos casos, especialmente quando lidamos com termos autoreferenciados ou combinadores que causam expansão infinita.

Observamos que a expressão começa a repetir a si mesma, indicando um ciclo infinito. Contudo, na ordem normal, como o argumento não é necessário para o resultado\;a redução pode ser concluída sem avaliá-lo.

Exemplo 2: Considere a expressão:

Vamos reduzir $M$ usando a ordem normal.

1. Identificamos o redex mais externo à esquerda:

   \[\underline{(\lambda x.\;(\lambda y.\;x))\;\left( (\lambda z.\;z + z)\;3 \right)}\;\left( (\lambda w.\;w\;w)\;(\lambda w.\;w\;w) \right)\]

   Aplicamos a redução beta ao redex, substituindo $x$ por $\left( (\lambda z.\;z + z)\;3 \right)$:

   \[\to_\beta\;(\lambda y.\;\left( (\lambda z.\;z + z)\;3 \right))\;\left( (\lambda w.\;w\;w)\;(\lambda w.\;w\;w) \right)\]

2. Observamos que a função resultante não utiliza o argumento $y$ no corpo da função. Portanto, o segundo argumento $\left( (\lambda w.\;w\;w)\;(\lambda w.\;w\;w) \right)$ não é avaliado na ordem normal, pois não é necessário.

3. Calculamos a expressão $(\lambda z.\;z + z)\;3$ no corpo da função:

   \[(\lambda z.\;z + z)\;3\;\to_\beta\;3 + 3 = 6\]

4. Substituímos o resultado no corpo da função:

   \[\lambda y.\;6\]

Este é o resultado da redução na ordem normal.

4.2. Ordem Aplicativa (Applicative-Order)

Na ordem aplicativa, a estratégia de redução no cálculo lambda consiste em avaliar primeiro os argumentos de uma função antes de aplicar a função em si. Isso significa que a redução ocorre das partes mais internas para as mais externas (redução interna). Essa abordagem corresponde à avaliação estrita, onde os argumentos são completamente avaliados antes da aplicação da função.

A ordem aplicativa é utilizada em muitas linguagens de programação, especialmente nas imperativas e em algumas funcionais, como ML e Scheme. Uma vantagem dessa estratégia é que, quando o resultado de um argumento é utilizado várias vezes no corpo da função, a avaliação prévia evita reavaliações redundantes, podendo ser mais eficiente em termos de tempo. No entanto, a ordem aplicativa pode levar a problemas de não-terminação em casos nos quais a ordem normal encontraria uma solução. E pode resultar em desperdício de recursos ao avaliar argumentos que não são necessários para o resultado da função.

Exemplo 1: Considere a expressão:

Na ordem aplicativa, avaliamos primeiro o argumento: Avaliamos o argumento $N = ((\lambda y.\;y\;y)\;(\lambda y.\;y\;y))$:

Aplicamos a redução beta:

Observamos que o termo se repete indefinidamente, resultando em uma redução infinita. Como o argumento não pode ser completamente avaliado, a aplicação da função não ocorre, e a redução não termina.

Na ordem normal, a função $(\lambda x.\;x)$ não utiliza o argumento além de retornar o próprio argumento. No entanto, na ordem aplicativa, a avaliação do argumento impede a conclusão da redução.

Exemplo 2: considere a expressão:

Na ordem aplicativa, procedemos da seguinte forma: avaliamos o primeiro argumento:

Calculamos $A = (\lambda z.\;z + 1)\;5$:

Avaliamos o segundo argumento:

Calculamos $B = (\lambda w.\;w \times 2)\;3$:

Aplicamos a função ao primeiro argumento avaliado:

Aplicamos a função resultante ao segundo argumento avaliado:

O resultado é $6\,$. Note que ambos os argumentos foram avaliados, embora o segundo argumento não seja utilizado no resultado . Isso exemplifica como a ordem aplicativa pode desperdiçar recursos ao avaliar argumentos desnecessários.

Exemplo 3: considere a expressão:

Na ordem aplicativa, avaliamos primeiro o argumento:

Avaliamos o argumento $N = (\lambda y.\;y\;y)\;(\lambda y.\;y\;y)$:

Aplicamos a redução beta:

O termo entra em uma redução infinita.

Como o argumento não pode ser completamente avaliado, a aplicação da função não ocorre, e a redução não termina. Na ordem normal, a função $(\lambda x.\;42)$ não utiliza o argumento $x\,$, portanto, o resultado seria imediatamente $42\,$, sem necessidade de avaliar o argumento que causa a não-terminação.

Exemplo 4: considere a expressão:

Na ordem aplicativa, procedemos assim:

Avaliamos o argumento $N = (\lambda x.\;x \times x)\,$, que é uma função e não requer avaliação adicional.

Aplicamos a função externa ao argumento:

Avaliamos o argumento interno $(\lambda x.\;x \times x)\;2$:

Aplicamos a redução beta:

Aplicamos a função externa ao resultado:

O resultado é $16\,$. Neste caso, a ordem aplicativa é eficiente, pois avalia os argumentos necessários e evita reavaliações.

A escolha entre ordem aplicativa e ordem normal depende do contexto e das necessidades específicas da computação. Em situações nas quais todos os argumentos são necessários e podem ser avaliados sem risco de não-terminação, a ordem aplicativa pode ser preferível. No entanto, quando há possibilidade de argumentos não terminarem ou não serem necessários, a ordem normal oferece uma estratégia mais segura.

4.3. Impactos em Linguagens de Programação

Haskell é uma linguagem de programação que utiliza avaliação preguiçosa, que corresponde à ordem normal. Isso significa que os argumentos só são avaliados quando absolutamente necessários, o que permite trabalhar com estruturas de dados potencialmente infinitas.

Exemplo 1:

naturals = [0..]
take 5 naturals
-- Retorna [0,1,2,3,4]

Aqui, a lista infinita naturals nunca é totalmente avaliada. Somente os primeiros 5 elementos são calculados, graças à avaliação preguiçosa.

Já o JavaScript usa avaliação estrita. Contudo, oferece suporte à avaliação preguiçosa por meio de geradores, que permitem gerar valores sob demanda.

Exemplo 2:

function* naturalNumbers() {
let n = 0;
While (True) yield n++;
}

const gen = naturalNumbers();
console.log(gen.next().value); // Retorna 0
console.log(gen.next().value); // Retorna 1

O código JavaScript do exemplo utiliza um gerador para criar uma sequência infinita de números naturais, produzidos sob demanda, um conceito semelhante à avaliação preguiçosa (lazy evaluation). Assim como na ordem normal de redução, na qual os argumentos são avaliados só, e quando necessários, o gerador naturalNumbers() só avalia e retorna o próximo valor quando o método next() é chamado. Isso evita a criação imediata de uma sequência infinita e permite o uso eficiente de memória, computando os valores exclusivamente quando solicitados, como ocorre na avaliação preguiçosa.

5. Equivalência Lambda e Definição de Igualdade

No cálculo lambda, a noção de equivalência vai além da simples comparação sintática entre dois termos. Ela trata de quando dois termos podem ser considerados igualmente computáveis ou equivalentes em um sentido mais profundo, independentemente de suas formas superficiais. Esta equivalência tem impactos na otimizações de programas, verificação de tipos e raciocínio em linguagens funcionais.

Dois termos lambda $M$ e $N$ são considerados equivalentes, denotado por $M\to_\beta N\,$, se podemos transformar um no outro através de uma sequência, possivelmente vazia de:

1. $\alpha$-reduções: que permitem a renomeação de variáveis ligadas, assegurando que a identidade de variáveis internas não afeta o comportamento da função.

2. $\beta$-reduções: que representam a aplicação de uma função ao seu argumento, o princípio básico da computação no cálculo lambda.

3. $\eta$-reduções: que expressam a extensionalidade de funções, permitindo igualar duas funções que se comportam da mesma forma quando aplicadas a qualquer argumento.

Extensionalidade refere-se ao princípio de que objetos ou funções são iguais se têm o mesmo efeito em todos os contextos possíveis. Em lógica, duas funções são consideradas extensionais se, para todo argumento, elas produzem o mesmo resultado. Em linguística, extensionalidade se refere a expressões cujo significado é determinado exclusivamente por seu valor de referência, sem levar em conta contexto ou conotação.

Formalmente, a relação $\to_\beta$ é a menor relação de equivalência que satisfaz as seguintes propriedades:

1. redução-$beta$: $(\lambda x.\;M)N \to_\beta M[N/x]$

   Isto significa que a aplicação de uma função $(\lambda x.\;M)$ a um argumento $N$ resulta na substituição de todas as ocorrências de $x$ em $M$ pelo valor $N\,$.

2. $\eta$-redução: $\lambda x.\;Mx\to_\beta M\,$, se $x$ não ocorre livre em $M$

   A $\eta$-redução captura a ideia de extensionalidade. Se uma função $\lambda x.\;Mx$ aplica $M$ a $x$ sem modificar $x\,$, ela é equivalente a $M\,$.

3. Compatibilidade com abstração: Se $M\to_\beta M’\,$, então $\lambda x.\;M\to_\beta \lambda x.\;M’$

   Isto garante que se dois termos são equivalentes, então suas abstrações, funções que os utilizam, serão equivalentes.

4. Compatibilidade com aplicação: Se $M\to_\beta M’$ e $N\to_\beta N’\,$, então $M\;N\to_\beta M’N’$

   Esta regra mostra que a equivalência se propaga para as aplicações de funções, mantendo a consistência da equivalência.

É importante notar que a ordem em que as reduções são aplicadas não afeta o resultado\;devido à propriedade de Church-Rosser do cálculo lambda. Isso garante que, independentemente de como o termo é avaliado, se ele tem uma forma normal, a avaliação eventualmente a encontrará.

A relação $\to_\beta$ é uma relação de equivalência, o que significa que ela possui três propriedades: é uma relação Reflexiva. Ou seja, para todo termo $M\,$, temos que $M\to_\beta M\,$. O que significa que qualquer termo é equivalente a si mesmo, o que é esperado; é uma relação Simétrica. Isso significa que se $M\to_\beta N\,$, então $N\to_\beta M\,$. Se um termo $M$ pode ser transformado em $N\,$, então o oposto é similarmente verdade. E, finalmente, é uma relação Transitiva. Neste caso, se $M\to_\beta N$ e $N\to_\beta P\,$, então $M\to_\beta P\,$. Isso implica que, se podemos transformar $M$ em $N$ e $N$ em $P\,$, então podemos transformar diretamente $M$ em $P\,$.

A equivalência $\to_\beta$ influencia o raciocínio sobre programas em linguagens funcionais, permitindo substituições e otimizações que preservam o significado computacional. As propriedades da equivalência $\to_\beta$ garantem que podemos substituir termos equivalentes em qualquer contexto, sem alterar o significado ou o resultado da computação. Em termos de linguagens de programação, isso permite otimizações e refatorações que preservam a correção do programa.

Neste ponto, a leitora deve estar ansiosa para ver alguns exemplos de equivalência.

1. Identidade e aplicação trivial:

   Exemplo 1:

   \[\lambda x.(\lambda y.\;y)x \to_\beta \lambda x.\;x\]

   Aqui, a função interna $\lambda y.\;y$ é a função identidade, que simplesmente retorna o valor de $x\,$. Após a aplicação, obtemos $\lambda x.\;x\,$, a função identidade.

   Exemplo 2:

   \[\lambda z.(\lambda w.w)z \to_\beta \lambda z.\;z\]

   Assim como no exemplo original, a função interna $\lambda w.w$ é a função identidade. Após a aplicação, o valor de $z$ é retornado.

   Exemplo 3:

   \[\lambda a.(\lambda b.b)a \to_\beta \lambda a.a\]

   A função $\lambda b.b$ é aplicada ao valor $a\,$, retornando o próprio $a\,$. Isso demonstra mais uma aplicação da função identidade.

2. Função constante:

   Exemplo 1:

   \[(\lambda x.\lambda y.x)M\;N \to_\beta M\]

   Neste exemplo, a função $\lambda x.\lambda y.x$ retorna sempre seu primeiro argumento, ignorando o segundo. Aplicando isso a dois termos $M$ e $N\,$, o resultado é simplesmente $M\,$.

   Exemplo 2:

   \[(\lambda a.\lambda b.a)P Q \to_\beta P\]

   A função constante $\lambda a.\lambda b.a$ retorna sempre o primeiro argumento ($P$), ignorando $Q\,$.

   Exemplo 3:

   \[(\lambda u.\lambda v.u)A B \to_\beta A\]

   Aqui, o comportamento é o mesmo: o primeiro argumento ($A$) é retornado, enquanto o segundo ($B$) é ignorado.

3. $\eta$-redução:

   Exemplo 1:

   \[\lambda x.(\lambda y.M)x \to_\beta \lambda x.\;M[x/y]\]

   Se $x$ não ocorre livre em $M\,$, podemos usar a $\eta$-redução para encurtar a expressão, pois aplicar $M$ a $x$ não altera o comportamento da função. Este exemplo mostra como podemos internalizar a aplicação, eliminando a dependência desnecessária de $x\,$.

   Exemplo 2:

   \[\lambda x.(\lambda z.N)x \to_\beta \lambda x.N[x/z]\]

   Similarmente, se $x$ não ocorre em $N\,$, a $\eta$-redução simplifica a expressão para $\lambda x.N\,$.

   Exemplo 3:

   \[\lambda f.(\lambda g.P)f \to_\beta \lambda f.P[f/g]\]

   Aqui, a $\eta$-redução elimina a aplicação de $f$ em $P\,$, resultando em $\lambda f.P\,$.

4. Termo $\Omega$(não-terminante):

   Exemplo 1:

   \[(\lambda x.\;\, x\;x)(\lambda x.\;\, x\;x) \to_\beta (\lambda x.\;\, x\;x)(\lambda x.\;\, x\;x)\]

   Este é o famoso combinador $\Omega$, que se reduz a si mesmo indefinidamente, criando um ciclo infinito de auto-aplicações. Apesar de não ter forma normal (não termina), ele é equivalente a si mesmo por definição.

   Exemplo 2:

   \[(\lambda f.\;f\;f)(\lambda f.\;f\;f) \to_\beta (\lambda f.\;f\;f)(\lambda f.\;f\;f)\]

   Assim como o combinador $\Omega\,$, este termo cria um ciclo infinito de auto-aplicação.

   Exemplo 3:

   \[(\lambda u.\;u\;u)(\lambda u.\;u\;u) \to_\beta (\lambda u.\;u\;u)(\lambda u.\;u\;u)\]

   Outra variação do combinador $\Omega\,$, que resulta em uma redução infinita sem forma normal.

5. Composição de funções:

   Exemplo 1:

   \[(\lambda f.\lambda g.\lambda x.\;f\;(g\;x))\;M\;N \to_\beta \lambda x.\;M\;(N\;x)\]

   Neste caso, a composição de duas funções, $M$ e $N\,$, é expressa como uma função que aplica $N$ ao argumento $x\,$, e então aplica $M$ ao resultado. A redução demonstra como a composição de funções pode ser representada e simplificada no cálculo lambda.

   Exemplo 2:

   \[(\lambda f.\lambda g.\lambda y.\;f\;(g\;y))\;A\;B \to_\beta \lambda y.\;A\;(B\;y)\]

   A composição de $A$ e $B$ é aplicada ao argumento $y\,$, e o resultado de $By$ é então passado para $A\,$.

   Exemplo 3:

   \[(\lambda h.\lambda k.\lambda z.\;h\;(k\;z))\;P\;Q \to_\beta \lambda z.\;P\;(Q\;z)\]

   Similarmente, a composição de $P$ e $Q$ é aplicada ao argumento $z\,$, e o resultado de $Qz$ é passado para $P\,$.

5.1. Equivalência Lambda e seu Impacto em Linguagens de Programação

A equivalência lambda influencia o desenvolvimento e a otimização de linguagens funcionais como Haskell e OCaml. Essa ideia de equivalência cria uma base forte para pensar na semântica dos programas de forma abstrata. Isso é essencial para a verificação formal e otimização automática.

Dois termos lambda $M$ e $N$ são considerados equivalentes, denotado por $M\to_\beta N\,$, se é possível transformar um no outro através de uma sequência (possivelmente vazia) de:

1. $\alpha$ - reduções (renomeação de variáveis ligadas)
2. $\beta$-reduções (aplicação de funções)
3. $\eta$-conversões (extensionalidade de funções)

Formalmente:

Talvez algumas aplicações em linguagem Haskell ajude a fixar os conceitos.

1. Eliminação de Código Redundante

   A equivalência lambda permite a substituição de expressões por versões mais simples sem alterar o comportamento do programa. Por exemplo:

   -- Antes da otimização
   let x = (\y -> Y + 1)\;5 in x * 2
   -- Após a otimização (equivalente)
   let x = 6 in x * 2
   

   Aqui, o compilador pode realizar a redução-$beta$ $(\lambda y.\;y + 1)\;5\to_\beta 6$ em tempo de compilação, simplificando o código.

2. Transformações Seguras de Código

   Os Compiladores podem aplicar refatorações automáticas baseadas em equivalências lambda. Por exemplo:

   -- Antes da transformação
   map (\x -> f (g x)) xs
   
   -- Após a transformação (equivalente)
   map (f . g) xs
   

   Esta transformação, baseada na lei de composição $f \circ g \equiv \lambda x.\;f(g(x))\,$, pode melhorar a eficiência e legibilidade do código.

3. Inferência de Tipos

   A equivalência lambda é crucial em sistemas de tipos avançados. Considere:

   -- Definição de uma função polimórfica f
   f :: (a -> b) -> ([a] -> [b])
   f g = map g
   -- Uso de f com a função show
   h :: ([Int] -> [String])
   h = f show
   
   -- Exemplo de uso
   main :: IO ()
   main = do
   let numbers = [1, 2, 3, 4, 5]
   print $ h numbers
   

   Neste exemplo:

   1. A função f é definida de forma polimórfica. Ela aceita uma função g de tipo a -> b e retorna uma função que mapeia listas de a para listas de b.

   2. A implementação de f usa map, que aplica a função g a cada elemento de uma lista.

   3. A função h é definida como uma aplicação de f à função show.

   4. O sistema de tipos de Haskell realiza as seguintes inferências: show tem o tipo Show a \Rightarrow a \rightarrow String. Ao aplicar f a show, o compilador infere que a = Int e b = String. Portanto, h tem o tipo [Int] -> [String].

   Esta inferência demonstra como a equivalência lambda é usada pelo sistema de tipos: f show é equivalente a map show. O tipo de map show é inferido como [Int] -> [String]. No main, podemos ver um exemplo de uso de h, que converte uma lista de inteiros em uma lista de strings.

   O sistema de tipos usa equivalência lambda para inferir que f show é um termo válido do tipo [Int] -> [String].

4. Avaliação Preguiçosa

Em Haskell, a equivalência lambda fundamenta a avaliação preguiçosa:

 expensive_computation :: Integer
 expensive_computation = sum [1..1000000000]

 lazy_example :: Bool -> Integer
 lazy_example condition =
 let x = expensive_computation
 in if condition then x + 1 else 0

 main :: IO ()
 main = do
 putStrLn _Avaliando com condition = True:_
 print $ lazy_example True
 putStrLn _Avaliando com condition = False:_
 print $ lazy_example False

Neste exemplo: expensive_computation é uma função que realiza um cálculo custoso (soma dos primeiros 1 bilhão de números inteiros).

lazy_example é uma função que demonstra a avaliação preguiçosa. Ela aceita um argumento booleano condition. Dentro de lazy_example, x é definido como expensive_computation, mas devido à avaliação preguiçosa, este cálculo não é realizado imediatamente.

Se condition for True, o programa calculará x + 1, o que forçará a avaliação de expensive_computation. Se condition for False, o programa retornará 0, e expensive_computation nunca é avaliado.

Ao executar este programa, a persistente leitora verá que: quando condition é True, o programa levará um tempo considerável para calcular o resultado. Quando condition é False, o programa retorna instantaneamente, pois expensive_computation não é avaliado.

Graças à equivalência lambda e à avaliação preguiçosa, expensive_computation só é avaliado se condition for verdadeira.

A equivalência Lambda, ainda que seja importante, não resolve todos os problemas possíveis. Alguns dos desafios estão relacionados com:

1. Indecidibilidade: Determinar se dois termos lambda são equivalentes é um problema indecidível em geral. Compiladores devem usar heurísticas e aproximações.

2. Efeitos Colaterais: Em linguagens com efeitos colaterais, a equivalência lambda pode não preservar a semântica do programa. Por exemplo:

   -- Estas expressões não são equivalentes em presença de efeitos colaterais
   f1 = (\x -> putStrLn (_Processando _ ++ show x) >> return (x + 1))
   f2 = \x -> do
   putStrLn (_Processando _ ++ show x)
   return (x + 1)
   
   main = do
      let x = f1 5
      Y <- x
      print y
   
      let z = f2 5
      w <- z
      print w
   

   Neste exemplo, f1 e f2 parecem equivalentes do ponto de vista do cálculo lambda puro. No entanto, em Haskell, que tem um sistema de I/O baseado em monads, elas se comportam diferentemente:

   • f1 cria uma ação de I/O que, quando executada, imprimirá a mensagem e retornará o resultado.
   • f2 de igual forma cria uma ação de I/O, mas a mensagem é impressa imediatamente quando f2 for chamada.

   Ao executar este programa, a incansável leitora verá que a saída para f1 e f2 é diferente devido ao momento em que os efeitos colaterais (impressão) ocorrem.

3. Complexidade Computacional: Mesmo quando decidível, verificar equivalências pode ser computacionalmente caro, exigindo um equilíbrio entre otimização e tempo de compilação.

6. Funções Recursivas e o Combinador Y

No cálculo lambda, uma linguagem puramente funcional, não há uma forma direta de definir funções recursivas. Isso acontece porque, ao tentar criar uma função que se refere a si mesma, como o fatorial, acabamos com uma definição circular que o cálculo lambda puro não consegue resolver. Uma tentativa ingênua de definir o fatorial seria:

Aqui, $\text{fac}$ aparece nos dois lados da equação, criando uma dependência circular. No cálculo lambda puro, não existem nomes ou atribuições; tudo se baseia em funções anônimas. Portanto, não é possível referenciar $\text{fac}$ dentro de sua própria definição.

No cálculo lambda, todas as funções são anônimas. Não existem variáveis globais ou nomes fixos para funções. As únicas formas de vincular variáveis são:

• Abstração lambda: $\lambda x.\;e\,$, na qual $x$ é um parâmetro e $e$ é o corpo da função.
• Aplicação de função: $(f\;a)\,$, na qual $f$ é uma função e $a$ é um argumento.

Não há um mecanismo para definir uma função que possa se referenciar diretamente. Na definição:

queremos que $\text{fac}$ possa chamar a si mesma. Mas no cálculo lambda puro:

1. Não há nomes persistentes: O nome $\text{fac}$ do lado esquerdo não está disponível no corpo da função à direita. Nomes em abstrações lambda são parâmetros locais.

2. Variáveis livres devem ser vinculadas: $\text{fac}$ aparece livre no corpo e não está ligada a nenhum parâmetro ou contexto. Isso viola as regras do cálculo lambda.

3. Sem referência direta a si mesmo: Não se pode referenciar uma função dentro de si mesma, pois não existe um escopo que permita isso.

Considere uma função simples no cálculo lambda:

Esta função está bem definida. Mas, se tentarmos algo recursivo:

O problema é o mesmo: $\text{loop}$ não está definido dentro do corpo da função. Não há como a função chamar a si mesma sem um mecanismo adicional.

Em linguagens de programação comuns, definimos funções recursivas porque o nome da função está disponível dentro do escopo. Em Haskell, por exemplo:

fac :: Int -> Int
fac 0 = 1
fac n = n * fac (n - 1)

Aqui, o nome fac está disponível em um dos casos da função para ser chamado recursivamente. No cálculo lambda, essa forma de vinculação não existe.

6.1. O Combinador $Y$ como Solução

Para contornar essa limitação, usamos o conceito de ponto fixo. Um ponto fixo de uma função $F$ é um valor $X$ tal que $F(X) \, = X\,$. No cálculo lambda, esse conceito é implementado por meio de combinadores de ponto fixo, sendo o mais conhecido o combinador $Y\,$, atribuído a Haskell Curry.

O combinador $Y$ é definido como:

Para ilustrar o funcionamento do Y-combinator na prática, vamos implementá-lo em Haskell e usá-lo para definir a função fatorial:

-- Definição do Y-combinator
y :: (a -> a) -> a
y f = f (y f)

-- Definição da função fatorial usando o Y-combinator
factorial :: Integer -> Integer
factorial = Y \f n -> if n == 0 then 1 else n * f (n - 1)

main :: IO ()
main = do
 print $ factorial 5 -- Saída: 120
 print $ factorial 10 -- Saída: 3628800

Neste exemplo, o Y-combinator (y) é usado para criar uma versão recursiva da função fatorial sem a necessidade de defini-la recursivamente de forma explícita. A função factorial é criada aplicando $Y$ a uma função que descreve o comportamento do fatorial, mas sem se referir diretamente a si mesma. Podemos estender este exemplo para outras funções recursivas, como a sequência de Fibonacci:

fibonacci :: Integer -> Integer
fibonacci = y $\f n -> if n <= 1 then n else f (n - 1) + f (n - 2)

main :: IO ()
main = do
 print $ map fibonacci [0..10] -- Saída: [0,1,1,2,3,5,8,13,21,34,55]

O Y-combinator, ou combinador-Y, tem uma propriedade interessante que a esforçada leitora deve entender:

Isso significa que $Y\;F$ é um ponto fixo de $F\,$, permitindo que definamos funções recursivas sem a necessidade de auto-referência explícita. Quando aplicamos o combinador $Y$ a uma função $F\,$, ele retorna uma versão recursiva de $F\,$.

Matematicamente, o combinador $Y$ cria a recursão ao forçar a função $F$ a se referenciar indiretamente. O processo ocorre:

1. Aplicamos o combinador $Y$ a uma função $F\,$.

2. O $Y$ retorna uma função que, ao ser chamada, aplica $F$ a si mesma repetidamente.

3. Essa recursão acontece até que uma condição de término, como o caso base de uma função recursiva, seja atingida.

Com o combinador $Y\,$, não precisamos declarar explicitamente a recursão. O ciclo de auto-aplicação é gerado automaticamente, transformando qualquer função em uma versão recursiva de si mesma.

6.2. Exemplo de Função Recursiva: Fatorial

Usando o combinador $Y\,$, podemos definir corretamente a função fatorial no cálculo lambda. O fatorial de um número $n$ será:

Aqui, utilizamos funções auxiliares como $\text{isZero}\,$, $\text{mult}$ (multiplicação), e $\text{pred}$ (predecessor), todas definíveis no cálculo lambda. O combinador $Y$ cuida da recursão, aplicando a função a si mesma até que a condição de parada ($n = 0$) seja atendida. Vamos ver isso com mais detalhes usando o combinador $Y$ para definir $\text{fac}$

1. Defina uma função auxiliar que recebe como parâmetro a função recursiva:

   \[\text{Fac} = \lambda f.\;\lambda n.\;\text{if } (n = 0)\;\text{then } 1\;\text{else } n \times (f\;(n - 1))\]

   Aqui, $\text{Fac}$ é uma função que, dado um função $f\,$, retorna outra função que calcula o fatorial usando $f$ para a chamada recursiva.

2. Aplique o combinador $Y$ a $\text{Fac}$ para obter a função recursiva:

   \[\text{fac} = Y\;\text{Fac}\]

Agora, $\text{fac}$ é uma função que calcula o fatorial de forma recursiva.

O combinador $Y$ aplica $\text{Fac}$ a si mesmo para $\text{fac}$ se expande indefinidamente, permitindo as chamadas recursivas sem referência direta ao nome da função.

Exemplo 1:

Vamos calcular $\text{fac}\;2$ usando o combinador Y.

Função Fatorial:

Expansão da Definição de $\text{fatorial}$:

Aplicamos $Y$ à função $\lambda f.\;\lambda n.\;\ldots$:

Então, teremos:

Expandindo o Combinador Y:

A amável leitora deve lembrar que o Combinador $Y$ é definido como:

Aplicando $Y$ à função $g = \lambda f.\;\lambda n.\;\ldots$:

Portanto,

Aplicando $\text{fatorial}$ a 2

Simplificando as Aplicações:

Primeira Aplicação:

Desta forma, $F = \lambda f.\;\lambda n.\;\text{if}\;(n = 0)\;1\;(n \times (f\;(n - 1)))\,$.

Aplicando o Primeiro: $\lambda x$

A atenta leitora deve ter notado que temos uma autorreferência:

Portanto,

Aplicando $F$ com $M$ e $n = 2$:

Então,

Como $2 \ne 0\,$, calculamos:

Calculando $M\;1$:

Precisamos calcular $M\;1\,$, onde $M$ será:

Então,

Novamente, temos:

Aplicando $F$ com $M$ e $n = 1$:

Então,

Como $1 \ne 0\,$, temos:

Calculando $M\;0$:

Aplicando $F$ com $n = 0$:

Como $0 = 0\,$, temos:

Concluindo os Cálculos:

Portanto, o cálculo do fatorial de 2 será:

Exemplo 2:

Agora, vamos verificar o cálculo de $\text{fatorial}\;3$ seguindo o mesmo procedimento.

Aplicando $\text{fatorial}$ a 3:

Onde $F$ e $M$ são como definidos anteriormente.

Aplicando $F$ com $n = 3$:

Como $3 \ne 0\,$, temos:

Calculando $M\;2$:

Seguindo o mesmo processo, teremos:

Calculando os Valores:

Portanto, o cálculo do fatorial de 3 será:

6.2.1. Função Fatorial Usando Funções de Ordem Superior

Vamos rever o combinador $Y\,$, desta vez, usando funções de ordem superior. Como cada função de ordem superior encapsula um conjunto de abstrações lambda reduzindo o número de reduções-$\beta$ necessário. Começamos definindo algumas funções:

1. $\text{isZero}$:

   \[\text{isZero} = \lambda n.\;n\;(\lambda x.\;\text{False})\;\text{True}\]

   Esta função deve retornar $TRUE$ se for aplicada a $0$ e $False$ para qualquer outro valor. Como podemos ver a seguir: Vamos avaliar a função $\text{isZero}$ aplicada primeiro ao número zero e depois ao número um para verificar seu funcionamento.

   1. Aplicando ao zero ($\text{isZero}\;0$):

      \[\begin{align*} \text{isZero}\;0 &= (\lambda n.\;n\;(\lambda x.\;\text{False})\;\text{True})\;(\lambda s.\lambda z.\;z) \\ &\to_\beta (\lambda s.\lambda z.\;z)\;(\lambda x.\;\text{False})\;\text{True} \\ &\to_\beta (\lambda z.\;z)\;\text{True} \\ &\to_\beta \text{True} \end{align*}\]

   2. Aplicando ao um ($\text{isZero}\;1$):

      \[\begin{align*} \text{isZero}\;1 &= (\lambda n.\;n\;(\lambda x.\;\text{False})\;\text{True})\;(\lambda s.\lambda z.\;s\;z) \\ &\to_\beta (\lambda s.\lambda z.\;s\;z)\;(\lambda x.\;\text{False})\;\text{True} \\ &\to_\beta (\lambda z.\;(\lambda x.\;\text{False})\;z)\;\text{True} \\ &\to_\beta (\lambda x.\;\text{False})\;\text{True} \\ &\to_\beta \text{False} \end{align*}\]

2. $\text{mult}$:

   \[\text{mult} = \lambda m.\;\lambda n.\;\lambda f.\;m\;(n\;f)\]

   Esta função deve multiplicar dois números naturais. Podemos ver o resultado da sua aplicação se:

   1. Substituir $m$ por $2$ e $n$ por $3$
   2. Avaliar todas as reduções beta
   3. Verificar se o resultado é $6$ em notação de Church

   Com estas condições satisfeitas, a curiosa leitora pode ver o resultado da aplicação $\text{mult}\; 3\;2$:

   \[\begin{align*} \text{mult}\;2\;3 &= (\lambda m.\;\lambda n.\;\lambda f.\;m\;(n\;f))\;(\lambda s.\;\lambda z.\;s\;(s\;z))\;(\lambda s.\;\lambda z.\;s\;(s\;(s\;z))) \\ \\ &\text{Primeiro, substituímos $m$ por $2$:} \\ &\to_\beta (\lambda n.\;\lambda f.\;(\lambda s.\;\lambda z.\;s\;(s\;z))\;(n\;f))\;(\lambda s.\;\lambda z.\;s\;(s\;(s\;z))) \\ \\ &\text{Agora, substituímos $n$ por $3$:} \\ &\to_\beta \lambda f.\;(\lambda s.\;\lambda z.\;s\;(s\;z))\;((\lambda s.\;\lambda z.\;s\;(s\;(s\;z)))\;f) \\ \\ &\text{Calculamos $(3\;f)$, que aplica $f$ três vezes:} \\ &\to_\beta \lambda f.\;(\lambda s.\;\lambda z.\;s\;(s\;z))\;(\lambda z.\;f\;(f\;(f\;z))) \\ \\ &\text{Agora aplicamos esta função duas vezes:} \\ &\to_\beta \lambda f.\;\lambda z.\;(\lambda z.\;f\;(f\;(f\;z)))\;((\lambda z.\;f\;(f\;(f\;z)))\;z) \\ \\ &\text{Continuamos as reduções:} \\ &\to_\beta \lambda f.\;\lambda z.\;f\;(f\;(f\;(f\;(f\;(f\;z))))) \\ \end{align*}\]

   O resultado $\lambda f.\;\lambda z.\;f\;(f\;(f\;(f\;(f\;(f\;z)))))$ é a representação do número $6$ em numerais de Church, mostrando que $2 \times 3 = 6$. A função aplica $f$ exatamente seis vezes ao argumento $z$, que é precisamente a definição do numeral de Church para $6$. Copy

3. $\text{pred}$ (Predecessor):

   \[\text{pred} = \lambda n.\;\lambda f.\;\lambda x.\;n\;(\lambda g.\;\lambda h.\;h\;(g\;f))\;(\lambda u.\;x)\;(\lambda u.\;u)\]

   Vamos avaliar a validade da função $\text{pred}$ aplicando a função predecessor de $2$. Esta função deve devolver o número natural imediatamente anterior ao número aplicado. A avaliação envolve várias etapas de redução beta:

   \[\begin{align*} \text{pred}\;2 &= (\lambda n.\;\lambda f.\;\lambda x.\;n\;(\lambda g.\;\lambda h.\;h\;(g\;f))\;(\lambda u.\;x)\;(\lambda u.\;u))\;(\lambda s.\;\lambda z.\;s\;(s\;z)) \\ \\ &\text{Substituímos $n$ por $2$:} \\ &\to_\beta \lambda f.\;\lambda x.\;(\lambda s.\;\lambda z.\;s\;(s\;z))\;(\lambda g.\;\lambda h.\;h\;(g\;f))\;(\lambda u.\;x)\;(\lambda u.\;u) \\ \\ &\text{Agora aplicamos $2$ à primeira função:} \\ &\to_\beta \lambda f.\;\lambda x.\;(\lambda z.\;(\lambda g.\;\lambda h.\;h\;(g\;f))\;((\lambda g.\;\lambda h.\;h\;(g\;f))\;z))\;(\lambda u.\;x)\;(\lambda u.\;u) \\ \\ &\text{Reduzimos a aplicação interna:} \\ &\to_\beta \lambda f.\;\lambda x.\;(\lambda g.\;\lambda h.\;h\;(g\;f))\;(\lambda g.\;\lambda h.\;h\;(g\;f))\;(\lambda u.\;x)\;(\lambda u.\;u) \\ \\ &\text{Continuamos as reduções:} \\ &\to_\beta \lambda f.\;\lambda x.\;(\lambda h.\;h\;((\lambda g.\;\lambda h.\;h\;(g\;f))\;f))\;(\lambda u.\;x)\;(\lambda u.\;u) \\ \\ &\text{Aplicamos à $(\lambda u.\;x)$:} \\ &\to_\beta \lambda f.\;\lambda x.\;(\lambda u.\;x)\;((\lambda g.\;\lambda h.\;h\;(g\;f))\;f)\;(\lambda u.\;u) \\ \\ &\text{Continuamos reduzindo:} \\ &\to_\beta \lambda f.\;\lambda x.\;f\;(f\;x) \\ \end{align*}\]

   O resultado $\lambda f.\;\lambda x.\;f\;(f\;x)$ é a representação do número $1$ em numerais de Church, mostrando que o predecessor de $2$ é $1$. A função $\text{pred}$ aplica $f$ exatamente uma vez a menos que o número original, que é precisamente o que desejávamos provar.

Agora vamos definir a função fatorial usando o Combinador $Y$ e as funções de ordem superior que acabamos de definir:

Exemplo 1: Primeiro relembremos a definição do fatorial usando o combinador de ponto fixo:

Agora vamos calcular $\text{fatorial}\;2$ passo a passo:

1. Iniciando com $n = 2$:

   \[\text{fatorial}\;2 = \text{if}\;(\text{isZero}\;2)\;1\;(\text{mult}\;2\;(\text{fatorial}\;(\text{pred}\;2)))\]

Vamos detalhar cada passo das reduções:

1. Avaliando $\text{isZero}\;2$:

 $$\begin{align*}
 \text{isZero}\;2 &= (\lambda n.\;n\;(\lambda x.\;\text{false})\;\text{true})\;(\lambda s.\lambda z.\;s\;(s\;z)) \\
 &\to_\beta (\lambda s.\lambda z.\;s\;(s\;z))\;(\lambda x.\;\text{false})\;\text{true} \\
 &\to_\beta \text{false}
 \end{align*}$$

 Como retornou $\text{false}$, avaliamos:

 $$\begin{align*}
 &= \text{mult}\;2\;(\text{fatorial}\;(\text{pred}\;2)) \\
 &= \text{mult}\;2\;(\text{fatorial}\;1) \quad \text{(pois mostramos anteriormente que $\text{pred}\;2 = 1$)}
 \end{align*}$$

3.  Para $\text{fatorial}\;1$, primeiro avaliamos $\text{isZero}\;1$:

$$\begin{align*}
 \text{isZero}\;1 &= (\lambda n.\;n\;(\lambda x.\;\text{false})\;\text{true})\;(\lambda s.\lambda z.\;s\;z) \\
 &\to_\beta (\lambda s.\lambda z.\;s\;z)\;(\lambda x.\;\text{false})\;\text{true} \\
 &\to_\beta \text{false}
 \end{align*}$$

 Então calculamos:

 $$\begin{align*}
 \text{fatorial}\;1 &= \text{mult}\;1\;(\text{fatorial}\;(\text{pred}\;1)) \\
 &= \text{mult}\;1\;(\text{fatorial}\;0) \quad \text{(pois $\text{pred}\;1 = 0$)}
 \end{align*}$$

4.  Para $\text{fatorial}\;0$, avaliamos $\text{isZero}\;0$:

$$\begin{align*}
 \text{isZero}\;0 &= (\lambda n.\;n\;(\lambda x.\;\text{false})\;\text{true})\;(\lambda s.\lambda z.\;z) \\
 &\to_\beta (\lambda s.\lambda z.\;z)\;(\lambda x.\;\text{false})\;\text{true} \\
 &\to_\beta \text{true}
 \end{align*}$$

 Como retornou $\text{true}$, temos:
 $$\text{fatorial}\;0 = 1$$

5.  Agora substituímos de volta:

$$\begin{align*}
 \text{fatorial}\;1 &= \text{mult}\;1\;(\text{fatorial}\;0) \\
 &= \text{mult}\;1\;1 \\
 &= 1 \quad \text{(pela definição de $\text{mult}$)}
 \end{align*}$$

 E finalmente:

 $$\begin{align*}
 \text{fatorial}\;2 &= \text{mult}\;2\;(\text{fatorial}\;1) \\
 &= \text{mult}\;2\;1 \\
 &= 2 \quad \text{(pela definição de $\text{mult}$)}
 \end{align*}$$

Assim, mostramos que $\text{fatorial}\;2 = 2$, mostrando cada passo da recursão e como os valores são calculados de volta até o Resultado. A função fatorial é um exemplo clássico de recursão. Mas, não é a única.

Podemos definir uma função de exponenciação recursiva, para calcular $m^n$ usando o cálculo lambda, como:

$$\text{power} = Y\;(\lambda f. \lambda m. \lambda n. \text{if}\;(\text{isZero}\;n)\;1\;(\text{mult}\;m\;(f\;m\;(\text{pred}\;n))))$$

Assim como fizemos no fatorial, o combinador $Y$ irá permitir a definição recursiva sem auto-referência explícita. Vamos calcular $2^2$ usando a função $\text{power}$ detalhando cada redução. Começamos aplicando $\text{power}\;2\;2$:

1.  Primeira aplicação ($n = 2$):

$$\begin{align*}
 \text{power}\;2\;2 &= \text{if}\;(\text{isZero}\;2)\;1\;(\text{mult}\;2\;(\text{power}\;2\;(\text{pred}\;2))) \\
 \\
 \text{isZero}\;2 &= (\lambda n.\;n\;(\lambda x.\;\text{false})\;\text{true})\;(\lambda s.\lambda z.\;s\;(s\;z)) \\
 &\to_\beta (\lambda s.\lambda z.\;s\;(s\;z))\;(\lambda x.\;\text{false})\;\text{true} \\
 &\to_\beta \text{false}
 \end{align*}$$

 Como $\text{isZero}\;2$ retorna $\text{false}$, continuamos:

 $$= \text{mult}\;2\;(\text{power}\;2\;(\text{pred}\;2))$$

2.  Calculando $\text{pred}\;2$:

$$\begin{align*}
 \text{pred}\;2 &\to_\beta 1 \quad \text{(como mostramos anteriormente)}
 \end{align*}$$

3.  Segunda aplicação ($n = 1$):

$$\begin{align*}
\text{power}\;2\;1 &= \text{if}\;(\text{isZero}\;1)\;1\;(\text{mult}\;2\;(\text{power}\;2\;(\text{pred}\;1))) \\
\\
\text{isZero}\;1 &= (\lambda n.\;n\;(\lambda x.\;\text{false})\;\text{true})\;(\lambda s.\lambda z.\;s\;z) \\
&\to_\beta (\lambda s.\lambda z.\;s\;z)\;(\lambda x.\;\text{false})\;\text{true} \\
&\to_\beta \text{false}
\end{align*}$$

Como $\text{isZero}\;1$ retorna $\text{false}$, continuamos:

$$= \text{mult}\;2\;(\text{power}\;2\;(\text{pred}\;1))$$

4.  Calculando $\text{pred}\;1$:

$$\begin{align*}
\text{pred}\;1 &\to_\beta 0
\end{align*}$$

5.  Terceira aplicação ($n = 0$):

$$\begin{align*}
\text{power}\;2\;0 &= \text{if}\;(\text{isZero}\;0)\;1\;(\text{mult}\;2\;(\text{power}\;2\;(\text{pred}\;0))) \\
\\
\text{isZero}\;0 &= (\lambda n.\;n\;(\lambda x.\;\text{false})\;\text{true})\;(\lambda s.\lambda z.\;z) \\
&\to_\beta (\lambda s.\lambda z.\;z)\;(\lambda x.\;\text{false})\;\text{true} \\
&\to_\beta \text{true}
\end{align*}$$

Como $\text{isZero}\;0$ retorna $\text{true}$:

$$\text{power}\;2\;0 = 1$$

6.  Substituindo de volta:

$$\begin{align*}
\text{power}\;2\;1 &= \text{mult}\;2\;(\text{power}\;2\;0) \\
&= \text{mult}\;2\;1 \\
&\to_\beta 2
\end{align*}$$

E, finalmente:

$$\begin{align*}
\text{power}\;2\;2 &= \text{mult}\;2\;(\text{power}\;2\;1) \\
&= \text{mult}\;2\;2 \\
&\to_\beta 4
\end{align*}$$

Assim, mostramos que $\text{power}\;2\;2 = 4$, ou seja, $2^2 = 4$ em números de Church.

## 6.3. A Função de Ackermann

A Função de [Ackermann](https://en.wikipedia.org/wiki/Wilhelm_Ackermann), $\phi$, definida em cálculo lambda usando o combinador Y, ocupa uma posição singular na teoria da computação. Ela foi descoberta durante as investigações sobre computabilidade no início do século XX, quando matemáticos buscavam entender os limites do que poderia ser calculado mecanicamente. No cálculo lambda, ela é expressa como:

$$\text{Ack} = Y\;(\lambda f.\;\lambda m.\;\lambda n.\;\text{if}\;(\text{isZero}\;m)\;(\text{succ}\;n)\;(\text{if}\;(\text{isZero}\;n)\;(f\;(\text{pred}\;m)\;1)\;(f\;(\text{pred}\;m)\;(f\;m\;(\text{pred}\;n)))))$$

Sua importância é devida porque esta Função de Ackermann foi a primeira função demonstrada ser computável, porém não primitiva recursiva. As funções recursivas primitivas eram consideradas suficientes para expressar qualquer cálculo matemático prático, pois incluíam operações básicas como adição, multiplicação, exponenciação e suas generalizações.

> Funções recursivas primitivas são uma classe de funções que podem ser construídas a partir de funções básicas usando apenas composição e recursão primitiva. Sem muita profundidade, podemos definir as funções recursivas primitivas são funções que podem ser computadas usando apenas laços *For*.
>
> Formalmente, começamos com:
>
> 1.  A função sucessor: $S(n) = n + 1$
> 2.  A função zero constante: $Z(n) = 0$
> 3.  As funções de projeção: $P^n_i(x_1,...,x_n) = x_i$
>
> E então permitimos duas operações para construir novas funções:
>
> 1.  **Composição**: Se $g$ é uma função de $k$ variáveis e $h_1,...,h_k$ são funções de $n$ variáveis, então podemos formar:
>
> $$f(x_1,...,x_n) = g(h_1(x_1,...,x_n),...,h_k(x_1,...,x_n))$$
>
> 2.  **Recursão Primitiva**: Se $g$ é uma função de $n$ variáveis e $h$ é uma função de $n+2$ variáveis, então podemos definir $f$ por:
>
> $$\begin{align*}
> f(x_1,...,x_n,0) &= g(x_1,...,x_n) \\
> f(x_1,...,x_n,y+1) &= h(x_1,...,x_n,y,f(x_1,...,x_n,y))
> \end{align*}$$
>
> Usando estas regras, podemos construir funções como: - Adição: $a + b$ (usando recursão em $b$ com $g(a) = a$ e $h(a,b,c) = S(c)$) - Multiplicação: $a \times b$ (usando recursão em $b$ com $g(a) = 0$ e $h(a,b,c) = c + a$) - Exponenciação: $a^b$ (usando recursão em $b$ com $g(a) = 1$ e $h(a,b,c) = c \times a$)Vamos detalhar cada uma destas construções:
>
> 1.  Para a adição $a + b$:
>
> -   Fazemos recursão em $b$
> -   O caso base $g(a) = a$ significa que $a + 0 = a$
> -   No passo recursivo, $h(a,b,c) = S(c)$ onde $c$ é o resultado de $a + b$, significa que:
>
> $$\begin{align*}
>  a + (b+1) &= S(a + b)
>  \end{align*}$$
>
> 2.  Para a multiplicação $a \times b$:
>
> -   Fazemos recursão em $b$
> -   O caso base $g(a) = 0$ significa que $a \times 0 = 0$
> -   No passo recursivo, $h(a,b,c) = c + a$ onde $c$ é o resultado de $a \times b$, significa que:
>
> $$\begin{align*}
>  a \times (b+1) &= (a \times b) + a
>  \end{align*}$$
>
> 3.  Para a exponenciação $a^b$:
>
> -   Fazemos recursão em $b$
> -   O caso base $g(a) = 1$ significa que $a^0 = 1$
> -   No passo recursivo, $h(a,b,c) = c \times a$ onde $c$ é o resultado de $a^b$, significa que:
>
> $$\begin{align*}
>  a^{b+1} &= a^b \times a
>  \end{align*}$$

A função de Ackermann é significativa por demonstrar os limites das funções recursivas primitivas. Ela possui duas propriedades cruciais:

1.  **Crescimento Ultra-Rápido**:

-   Para qualquer função primitiva recursiva $f(n)$, existe algum $k$ onde $A(2,k)$ cresce mais rapidamente que $f(n)$

-   Por exemplo, $A(4,2)$ já é um número tão grande que excede a quantidade de átomos no universo observável

2.  **Recursão Não-Primitiva**:

-   Em funções recursivas primitivas, o valor recursivo $f(x_1,...,x_n,y)$ só pode aparecer como último argumento de $h$

-   A Ackermann usa o valor recursivo para gerar novos valores recursivos. Por exemplo:

$$\begin{align*}
  A(m,n) &= n + 1 &\text{se } m = 0 \\
  A(m,n) &= A(m-1,1) &\text{se } m > 0 \text{ e } n = 0 \\
  A(m,n) &= A(m-1,A(m,n-1)) &\text{se } m > 0 \text{ e } n > 0
  \end{align*}$$

Este resultado demonstra que existem funções computáveis que não podem ser capturadas pelo esquema de recursão primitiva, motivando definições mais gerais de computabilidade como as Máquinas de Turing. Esta descoberta estabeleceu uma hierarquia de funções computáveis, onde funções como fatorial e exponenciação ocupam níveis relativamente baixos, enquanto a função de Ackermann transcende toda esta hierarquia. Em termos práticos, sua implementação em cálculo lambda serve como um teste rigoroso para sistemas que lidam com recursão profunda, pois mesmo valores pequenos como $\text{Ack}\;4\;2$ geram números astronomicamente grandes. Isto a torna uma ferramenta valiosa para testar otimizações de compiladores e explorar os limites práticos da computação recursiva.

A Função de Ackermann:

$$\text{Ack} = Y\;(\lambda f.\;\lambda m.\;\lambda n.\;\text{if}\;(\text{isZero}\;m)\;(\text{succ}\;n)\;(\text{if}\;(\text{isZero}\;n)\;(f\;(\text{pred}\;m)\;1)\;(f\;(\text{pred}\;m)\;(f\;m\;(\text{pred}\;n)))))$$

É composta por:

1.  **Estrutura Base**:

$$\text{Ack} = Y\;(\lambda f.\;\lambda m.\;\lambda n.\;[\text{expressão}])$$

Onde: $Y$ é o combinador de ponto fixo que permite a recursão; $f$ é a própria função (recursão) e $m$ e $n$ são os argumentos da função

2.  **Primeiro Caso** (quando $m = 0$):

$$\text{if}\;(\text{isZero}\;m)\;(\text{succ}\;n)$$

Onde: se $m = 0$, retorna $n + 1$

Exemplo: $\text{Ack}(0,n) = n + 1$

3.  **Segundo Caso** (quando $m > 0$ e $n = 0$):

    $$\text{if}\;(\text{isZero}\;n)\;(f\;(\text{pred}\;m)\;1)$$

    Onde: se $n = 0$, calcula $\text{Ack}(m-1,1)$

    Exemplo: $\text{Ack}(m,0) = \text{Ack}(m-1,1)$

4.  **Terceiro Caso** (quando $m > 0$ e $n > 0$):

    $$f\;(\text{pred}\;m)\;(f\;m\;(\text{pred}\;n))$$

    Aqui calculamos $\text{Ack}(m-1,\text{Ack}(m,n-1))$ É uma recursão dupla:

    1.  Calcula $\text{Ack}(m,n-1)$ internamente
    2.  Usa esse resultado como segundo argumento para $\text{Ack}(m-1,\_)$

5.  **Funções Auxiliares**:

-   $\text{isZero}$: testa se um número é zero
-   $\text{pred}$: retorna o predecessor de um número
-   $\text{succ}$: retorna o sucessor de um número

As funções $\text{isZero}$ e $\text{pred}$ foram estudadas anteriormente, falta $\text{succ}$.

$$\text{succ} = \lambda n.\lambda f.\lambda x.f(n\;f\;x)$$

Aqui temos: $n$ é um número de Church ($\lambda f.\lambda x.f^n(x)$) e o resultado será o resultado será o número de Church imediatamente posterior a $n$, representando $n + 1$. Para entender esta função vamos realizar a redução completa de $\text{succ}\;2$, onde $2 = \lambda f.\lambda x.f(f(x))$:

$$\begin{align*}
   \text{succ}\;2 &= (\lambda n.\lambda f.\lambda x.f(n\;f\;x))\;(\lambda f.\lambda x.f(f(x))) \\
   &\rightarrow_\beta \lambda f.\lambda x.f((\lambda f.\lambda x.f(f(x)))\;f\;x) \\
   &\rightarrow_\beta \lambda f.\lambda x.f((\lambda x.f(f(x)))\;x) \\
   &\rightarrow_\beta \lambda f.\lambda x.f(f(f(x))) \\
   \end{align*}$$

O resultado $\lambda f.\lambda x.f(f(f(x)))$ é a representação de Church do número $3$, o número imediatamente posterior a $2$. Se a curiosa leitora desejar, pode verificar que este é realmente o número $3$, se aplicá-lo a qualquer função $f$ e argumento $x$:

$$(\lambda f.\lambda x.f(f(f(x))))\;g\;a \rightarrow_\beta^* g(g(g(a)))$$

Finalmente podemos fazer uma aplicação da Função de Ackermann usando apenas cálculo lambda puro:

Vamos calcular $\text{Ack}(1,1)$ usando cálculo lambda puro. Para clareza, usaremos a seguinte notação: números de Church: $\underline{n}$ representa o número $n$; $Y$ é o combinador de ponto fixo e omitiremos algumas reduções do $Y$ por clareza.

$$\begin{align*}
   \text{Ack}(1,1) &= Y\;(\lambda f.\;\lambda m.\;\lambda n.\;\text{if}\;(\text{isZero}\;m)\;(\text{succ}\;n)\;(\text{if}\;(\text{isZero}\;n)\;(f\;(\text{pred}\;m)\;\underline{1})\;(f\;(\text{pred}\;m)\;(f\;m\;(\text{pred}\;n)))))\;\underline{1}\;\underline{1} \\
   &\rightarrow_\beta \text{if}\;(\text{isZero}\;\underline{1})\;(\text{succ}\;\underline{1})\;(\text{if}\;(\text{isZero}\;\underline{1})\;(\text{Ack}\;(\text{pred}\;\underline{1})\;\underline{1})\;(\text{Ack}\;(\text{pred}\;\underline{1})\;(\text{Ack}\;\underline{1}\;(\text{pred}\;\underline{1})))) \\
   &\rightarrow_\beta \text{if}\;(\text{false})\;(\text{succ}\;\underline{1})\;(\text{if}\;(\text{false})\;(\text{Ack}\;\underline{0}\;\underline{1})\;(\text{Ack}\;\underline{0}\;(\text{Ack}\;\underline{1}\;\underline{0}))) \\
   &\rightarrow_\beta \text{Ack}\;\underline{0}\;(\text{Ack}\;\underline{1}\;\underline{0}) \\
   &\rightarrow_\beta \text{Ack}\;\underline{0}\;(\text{Ack}\;\underline{0}\;\underline{1}) \\
   &\rightarrow_\beta \text{Ack}\;\underline{0}\;(\text{succ}\;\underline{1}) \\
   &\rightarrow_\beta \text{Ack}\;\underline{0}\;\underline{2} \\
   &\rightarrow_\beta \text{succ}\;\underline{2} \\
   &\rightarrow_\beta \underline{3}
   \end{align*}$$

Portanto, $\text{Ack}(1,1) = 3$. A observadora leitora de perceber que: o primeiro argumento $m = 1$ é não-zero, então avaliamos o segundo `if`; o segundo argumento $n = 1$ é não-zero, então calculamos $\text{Ack}(0,\text{Ack}(1,0))$; $\text{Ack}(1,0)$ reduz para $\text{Ack}(0,1)$ que reduz para $2$. Finalmente, $\text{Ack}(0,2)$ reduz para $3$

Sem usar a notação de números de Church, é possível simplificar a Função de Ackermann:

$$\begin{align*}
   \text{Ack} = Y\;(&\lambda f.\;\lambda m.\;\lambda n.\\
   &\lambda s.\;\lambda z.\\
   &m\;(\lambda x.n\;(\lambda y.f\;x\;(f\;m\;y\;s\;z)\;s\;z)\;(\lambda y.f\;x\;(\lambda s.\lambda z.z)\;s\;z))\;(\lambda x.n\;s\;z))
   \end{align*}$$

Onde: $Y$ é o combinador de ponto fixo $\lambda f.(\lambda x.f(x\;x))(\lambda x.f(x\;x))$; cada número $n$ é representado como $\lambda s.\lambda z.s^n(z)$; o teste $\text{isZero}$ está embutido em $m$ e $n$ através da aplicação de booleanos de Church; a redução de $\text{pred}$ acontece naturalmente na aplicação $x$ dentro de $m$; finalmente, o $\text{succ}$ está representado pela própria aplicação de $s$;

Por exemplo, para $\text{Ack}(1,1)$:

$$\begin{align*}
   \text{Ack}\;&(\lambda s.\lambda z.s(z))\;(\lambda s.\lambda z.s(z)) \\
   &\rightarrow_\beta^* \lambda s.\lambda z.s(s(s(z)))
   \end{align*}$$

Esta é a forma onde cada operação é reduzida aos seus elementos mais básicos de abstração e aplicação.

A capacidade do cálculo lambda de expressar a função de Ackermann usando apenas funções anônimas e o combinador Y demonstra sua completude computacional de uma forma que vai além das meras definições recursivas de operações aritméticas básicas. Ela mostra que mesmo funções que transcendem a recursão primitiva podem ser expressas no minimalismo do cálculo lambda.

# 7. Estruturas de Dados Simples

As estruturas de dados são componentes da ciência da computação, e sua representação em diferentes modelos computacionais permite compreender suas propriedades e manipulações. Este capítulo explora números naturais e valores booleanos, na ótica do cálculo lambda. Começamos investigando como os números naturais são codificados usando apenas funções, através dos números de Church, e suas operações aritméticas básicas. Em seguida, exploramos como a lógica proposicional é implementada no mesmo framework.

No cálculo lambda, os números naturais são representados como funções de ordem superior que aplicam uma função $f$ a um argumento $x$ um número específico de vezes. Por exemplo, o número $2$ é representado como $\lambda s. \lambda z. s\;(s\;z)$, que aplica a função $s$ duas vezes ao argumento $z$. Esta representação permite implementar todas as operações aritméticas como manipulações dessas funções.

A lógica proposicional é construída começando com a representação dos valores verdade como funções que selecionam entre dois argumentos: $\text{True} = \lambda x. \lambda y. x$ e $\text{False} = \lambda x. \lambda y. y$. A partir dessa base, todas as operações lógicas - negação, conjunção, disjunção e outras - são implementadas como combinações dessas funções fundamentais, demonstrando como o cálculo lambda codifica não apenas números, mas também lógica e controle de fluxo.

## 7.1 Representação de Números Naturais no Cálculo Lambda

Estudar cálculo lambda após a álgebra abstrata nos faz pensar numa relação entre a representação dos números naturais por Church e a definição dos números naturais de [Georg Cantor](https://en.wikipedia.org/wiki/Georg_Cantor). Embora estejam em contextos teóricos diferentes, ambos tentam capturar a essência dos números naturais com estruturas básicas distintas.

Cantor é conhecido por seu trabalho na teoria dos conjuntos. Ele definiu os números naturais como um conjunto infinito e ordenado, começando do $0$ e progredindo com o operador sucessor. Para Cantor, cada número natural é construído a partir do anterior por meio de uma sucessão bem definida. O número $1$ é o sucessor de $0\,$, o número $2$ é o sucessor de $1\,$, e assim por diante. Esta estrutura fornece uma base sólida para a aritmética dos números naturais, especialmente na construção de conjuntos infinitos e na cardinalidade.

Enquanto Cantor desenvolveu sua teoria baseada em conjuntos e sucessores, Church adotou uma abordagem funcional. Em vez de tratar os números como elementos de um conjunto, Church os define como funções que operam sobre outras funções. Isso permite realizar a aritmética de forma puramente funcional. Esta diferença reflete duas abstrações dos números naturais, ambas capturando sua essência recursiva, mas com ferramentas matemáticas diferentes.

A ligação entre essas abordagens está no conceito de sucessor e na construção incremental e recursiva dos números. Embora Cantor e Church tenham trabalhado em áreas distintas — Cantor na teoria dos conjuntos e Church no cálculo lambda —, ambos representam os números naturais como entidades geradas de forma recursiva.

Agora podemos explorar os números de Church.

Os números de Church são uma representação elegante dos números naturais no cálculo lambda puro. Essa representação além de permitir a codificação dos números naturais, permite a implementação de operações aritméticas.

A ideia central dos números de Church é representar o número $n$ como uma função $f\,$. Essa função aplica outra função $f$ $n$ vezes a um argumento $x\,$. Formalmente, o número de Church para $n$ será:

$$n = \lambda s. \lambda z.\;s^n\;(z)$$

Aqui, $s^n(z)$ significa aplicar $s$ a $z\,$, $n$ vezes. $s$ representa o sucessor, e $z$ representa zero. Essa definição captura a essência dos números naturais: zero é a base, e cada número seguinte é obtido aplicando a função sucessor repetidamente.

Os primeiros números naturais podem ser representados:

-   $0 = \lambda s. \lambda z.\;z$
-   $1 = \lambda s. \lambda z. s\;(z)$
-   $2 = \lambda s. \lambda z. s\;(s\;(z))$
-   $3 = \lambda s. \lambda z. s\;(s\;(s\;(z)))$

A representação dos números naturais no cálculo lambda permite definir funções que operam sobre esses números.

A função sucessor, que incrementa um número natural como sucessor de outro número natural, é definida como:

$$\text{succ} = \lambda n. \lambda s. \lambda z.\;s\;(n\;s\;z)$$

A **função sucessor** é essencial para entender como os números naturais são criados. No entanto, para que os números de Church sejam considerados números naturais, é preciso implementar operações aritméticas no cálculo lambda puro. Para entender como isso funciona na prática, vamos aplicar $\text{succ}$ ao número $2$:

$$
\begin{aligned}
\text{succ }\;2 &= (\lambda n. \lambda s. \lambda z.\;s(n\;s\;z)) (\lambda s. \lambda z.\;s\;(s\;(z))) \\
&= \lambda s. \lambda z.\;s((\lambda s. \lambda z.\;s\;(s\;(z)))\;s\;z) \\
&= \lambda s. \lambda z.\;s\;(s\;(s\;(z))) \\
&= 3
\end{aligned}
$$

A **adição** entre dois números de Church, $m$ e $n\,$, pode ser definida como:

$$\text{add} = \lambda m. \lambda n. \lambda s. \lambda z.\;m\;s\;(n\;s\;z)$$

Essa definição funciona aplicando $n$ vezes a função $s$ ao argumento $z\,$, representando o número $n\,$. Em seguida, aplica $m$ vezes a função $s$ ao resultado anterior, somando $m$ e $n\,$. Isso itera sobre $n$ e depois sobre $m\,$, combinando as duas operações para obter a soma. Vamos ver um exemplo:

Vamos usar os números de Church para calcular a soma de $2 + 3$ em cálculo lambda puro. Primeiro, representamos os números $2$ e $3$ usando as definições de números de Church:

$$2 = \lambda s. \lambda z.\;s\;(s\;z)$$

$$3 = \lambda s. \lambda z.\;s\;(s\;(s\;z))$$

Agora, aplicamos a função de adição de números de Church:

$$\text{add} = \lambda m. \lambda n. \lambda s. \lambda z.\;m\;s\;(n\;s\;z)$$

Substituímos $m$ por $2$ e $n$ por $3$:

$$\text{add}\;2\;3 = (\lambda m. \lambda n. \lambda s. \lambda z.\;m\;s\;(n\;s\;z))\;2\;3$$

Expandimos a função:

$$= \lambda s. \lambda z. 2\;s\;(3\;s\;z)$$

Substituímos as representações de $2$ e $3$:

$$= \lambda s. \lambda z. (\lambda s. \lambda z. s\;(s\;z))\;s\;( (\lambda s. \lambda z. s\;(s\;(s\;z)))\;s\;z)$$

Primeiro, resolvemos o termo $3\;s\;z$:

$$= s\;(s\;(s\;z))$$

Agora, aplicamos $2\;s$ ao resultado:

$$= s\;(s\;(s\;(s\;(s\;z))))$$

E chegamos ao aninhamento de cinco funções o que representa $5\,$, ou seja, o resultado de $2 + 3$ em cálculo lambda puro.

A **multiplicação** de dois números de Church, $m$ e $n\,$, é expressa assim:

$$\text{mult} = \lambda m. \lambda n. \lambda s. m\;(n\;s)$$

Nesse caso, a função $n\;s$ aplica $s\,$, $n$ vezes, representando o número $n\,$. Então, aplicamos $m$ vezes essa função, resultando em $s$ sendo aplicada $m \times n$ vezes. A multiplicação, portanto, é obtida através da repetição combinada da aplicação de $s\,$. Vamos usar os números de Church para calcular a multiplicação de $2 \times 2$ em cálculo lambda puro. Primeiro, representamos o número $2$ usando a definição de números de Church:

$$2 = \lambda s. \lambda z.\;s\;(s\;z)$$

Agora, aplicamos a função de multiplicação de números de Church:

$$\text{mult} = \lambda m. \lambda n. \lambda s.\;m\;(n\;s)$$

Substituímos $m$ e $n$ por $2$:

$$\text{mult}\;2\;2 = (\lambda m. \lambda n. \lambda s.\;m\;(n\;s))\;2\;2$$

Expandimos a função:

$$= \lambda s. 2\;(2\;s)$$

Substituímos a representação de $2$:

$$= \lambda s. (\lambda s. \lambda z. s\;(s\;z))\;(2\;s)$$

Agora resolvemos o termo $2\;s$:

$$2\;s = \lambda z.\;s\;(s\;z)$$

Substituímos isso na expressão original:

$$= \lambda s. (\lambda z.\;s\;(s\;z))$$

Agora aplicamos a função $2\;s$ mais uma vez:

$$= \lambda s. \lambda z.\;s\;(s\;(s\;(s\;z)))$$

O que representa $4\,$, ou seja, o resultado de $2 \times 2$ em cálculo lambda puro.

A exponenciação, por sua vez, é dada pela fórmula:

$$\text{exp} = \lambda b. \lambda e.\;e\;b$$

Aqui, a função $e\;b$ aplica $b\,$, $e$ vezes. Como $b$ já é um número de Church, aplicar $e$ vezes sobre ele significa calcular $b^e\,$. A exponenciação é realizada repetindo a aplicação da base $b$ sobre si mesma, $e$ vezes. Vamos usar os números de Church para calcular a exponenciação $2^2$ em cálculo lambda puro. Primeiro, representamos o número $2$ usando a definição de números de Church:

$$2 = \lambda s. \lambda z.\;s\;(s\;z)$$

Agora, aplicamos a função de exponenciação de números de Church:

$$\text{exp} = \lambda b. \lambda e.\;e\;b$$

Substituímos $b$ e $e$ por $2$:

$$\text{exp}\;2\;2 = (\lambda b. \lambda e.\;e\;b)\;2\;2$$

Expandimos a função:

$$= 2\;2$$

Agora substituímos a representação de $2$ no lugar de $e$:

$$= (\lambda s. \lambda z.\;s\;(s\;z))\;2$$

Agora aplicamos $2$ a $b$:

$$= (\lambda z.\;2\;(2\;z))$$

Substituímos a definição de $2$ para ambos os termos:

$$= \lambda z. (\lambda s. \lambda z.\;s\;(s\;z))\;(\lambda s. \lambda z. s\;(s\;z))\;z$$

Aplicamos a função de $2$:

$$= \lambda z. \lambda s.\;s\;(s\;(s\;(s\;z)))$$

O que representa $4\,$, ou seja, o resultado de $2^2$ em cálculo lambda puro.

Agora, que vimos três operações básicas, podemos expandir o conceito de números de Church e incluir mais operações aritméticas.

A subtração pode ser definida de forma mais complexa, utilizando combinadores avançados como o **combinador de predecessor**. A definição é a seguinte:

$$
\text{pred} = \lambda n. \lambda f. \lambda x.\;n (\lambda g. \lambda h.\;h\;(g\;f)) (\lambda u.\;x) (\lambda u.\;u)
$$

Esta função retorna o predecessor de $n\,$, ou seja, o número $n - 1\,$. Vamos ver um exemplo de aplicação da função $\text{pred}$ e calcular o predecessor de $3\,$.

$$
\begin{aligned}
\text{pred }\;3 &= (\lambda n. \lambda f. \lambda x.\;n (\lambda g. \lambda h.\;h\;(g\;f)) (\lambda u.\;x) (\lambda u. u)) (\lambda s. \lambda z.\;s(\;s(\;s\;(z)))) \\
&= \lambda f. \lambda x.\;(\lambda s. \lambda z.\;s(\;s(\;s\;(z)))) (\lambda g. \lambda h.\;h\;(g\;f)) (\lambda u.\;x) (\lambda u.\;u) \\
&= \lambda f. \lambda x.\;f\;(f\;(x)) \\
&= 2
\end{aligned}
$$

Podemos definir a divisão como uma sequência de subtrações sucessivas e construir uma função $\text{div}$ que calcule quocientes utilizando $\text{pred}$ e $\text{mult}\,$. A expansão para números inteiros pode ser feita definindo funções adicionais para lidar com números negativos.

Para definir números negativos, e assim representar o conjunto dos números inteiros, em cálculo lambda puro, usamos **pares de Church**. Cada número é representado por dois contadores: um para os sucessores (números positivos) e outro para os predecessores (números negativos). Assim, podemos simular a existência de números negativos. O número zero é definido assim:

$$\text{zero} = \lambda s. \lambda p.\;p$$

Um número positivo, como $2\,$, seria definido assim:

$$\text{positive-2} = \lambda s. \lambda p.\;s\;(s\;p)$$

Um número negativo, como $-2\,$, seria:

$$\text{negative-2} = \lambda s. \lambda p.\;p\;(p\;s)$$

Para manipular esses números, precisamos de funções de sucessor e predecessor. A função de sucessor, que incrementa um número, é definida assim:

$$\text{succ} = \lambda n. \lambda s. \lambda p.\;s\;(n\;s\;p)$$

A função de predecessor, que decrementa um número, será:

$$\text{pred} = \lambda n. \lambda s. \lambda p. p\;(n\;s\;p)$$

Com essas definições, podemos representar e manipular números positivos e negativos. Sucessores são aplicados para aumentar números positivos, e predecessores são usados para aumentar números negativos.

Agora que temos uma representação para números negativos, vamos calcular a soma de $3 + (-2)$ usando cálculo lambda puro. Primeiro, representamos os números $3$ e $-2$ usando as definições de pares de Church:

$$3 = \lambda s. \lambda p.\;s\;(s\;(s\;p))$$

$$-2 = \lambda s. \lambda p.\;p\;(p\;s)$$

A função de adição precisa ser adaptada para lidar com pares de Church (positivos e negativos). Aqui está a nova definição de adição:

$$\text{add} = \lambda m. \lambda n. \lambda s. \lambda p.\;m\;s\;(n\;s\;p)$$

Substituímos $m$ por $3$ e $n$ por $-2$:

$$\text{add}\;3\;(-2) \, = (\lambda m. \lambda n. \lambda s. \lambda p.\;m\;s\;(n\;s\;p))\;3\;(-2)$$

Expandimos a função:

$$= \lambda s. \lambda p.\;3\;s\;(-2\;s\;p)$$

Substituímos a representação de $3$ e $-2$:

$$= \lambda s. \lambda p. (\lambda s. \lambda p.\;s\;(s\;(s\;p)))\;s\;((\lambda s. \lambda p.\;p\;(p\;s))\;s\;p)$$

Resolvemos primeiro o termo $-2\;s\;p$:

$$= p\;(p\;s)$$

Agora aplicamos o termo $3\;s$ ao resultado:

$$= s\;(s\;(p\;s))$$

O que representa $1\,$, ou seja, o resultado de $3 + (-2)$ em cálculo lambda puro.

Para implementar a divisão corretamente no cálculo lambda puro, precisamos do combinador $Y\,$, que permite recursão. O combinador $Y$ veremos o combinador $Y$ com mais cuidado em outra parte deste texto, por enquanto, basta saber que ele é definido assim:

$$Y = \lambda f. (\lambda x. f\;(x\;x)) (\lambda x. f\;(x\;x))$$

Agora, podemos definir a função de divisão com o combinador $Y\,$. Primeiro, definimos a lógica de subtração repetida:

$$\text{divLogic} = \lambda f. \lambda m. \lambda n. \lambda s. \lambda z.\;\text{ifZero}\;(\text{sub}\;m\;n)\;z\;(\lambda q. \text{succ}\;(f\;(\text{sub}\;m\;n)\;n\;s\;z))$$

Aplicamos o combinador $Y$ para permitir a recursão:

$$\text{div} = Y\;\text{divLogic}$$

Para chegar a divisão precisamos utilizar o combinador $Y$ que permite a recursão necessária para subtrair repetidamente o divisor do dividendo. A função $\text{ifZero}\,$, que não definimos anteriormente usada para verificar se o resultado da subtração é zero ou negativo. A função $\text{sub}$ subtrai $n$ de $m\,$. Finalmente usamos a função $\text{succ}$ para contar quantas vezes subtraímos o divisor.

A capacidade de representar números e operações aritméticas no cálculo lambda mostra que ele pode expressar computações lógicas e funcionais e manipulações concretas de números. Isso mostra que o cálculo lambda pode representar qualquer função computável, como afirma a Tese de Church-Turing.

Ao definir números inteiros — positivos, negativos, e zero — e as operações de adição, subtração, multiplicação e divisão, o cálculo lambda mostra que pode ser uma base teórica para linguagens de programação que manipulam dados numéricos. Isso ajuda a entender a relação entre matemática e computação.

Definir números inteiros e operações básicas no cálculo lambda demonstra a universalidade do sistema. Ao mostrar que podemos modelar aritmética e computação de forma puramente funcional, o cálculo lambda prova que pode representar qualquer função computável, inclusive as aritméticas.

Já que modelamos a aritmética podemos avançar para a implementação desses conceitos em Haskell, começando pelos números de Church:

``` haskell
-- Números de Church em Haskell
type Church a = (a -> a) -> a -> a

zero :: Church a
zero = \f -> \x -> x

one :: Church a
one = \f -> \x -> f\;x

two :: Church a
two = \f -> \x -> f (f\;x)

three :: Church a
three = \f -> \x -> f (f (f\;x))

-- Função sucessor
succ' :: Church a -> Church a
succ' n = \f -> \x -> f (n f\;x)

-- Adição
add :: Church a -> Church a -> Church a
add m n = \f -> \x -> m f (n f\;x)

-- Multiplicação
mult :: Church a -> Church a -> Church a
mult m n = \f -> m (n f)

-- Conversão para Int
toInt :: Church Int -> Int
toInt n = n (+1) 0

-- Testes
main = do
 print (toInt zero) -- Saída: 0
 print (toInt one) -- Saída: 1
 print (toInt two) -- Saída: 2
 print (toInt three) -- Saída: 3
 print (toInt (succ' two)) -- Saída: 3
 print (toInt (add two three)) -- Saída: 5
 print (toInt (mult two three)) -- Saída: 6

Haskell é uma linguagem de programação funcional que, talvez, a curiosa leitora ainda não a conheça. Por isso, vamos explorar a implementação das operações aritméticas dos números de Church (adição e multiplicação) em C++20 e Python. Vamos ver como essas operações são transformações e como podemos implementá-las em linguagens imperativas.

A função sucessor aplica uma função $f$ a um argumento $z$ uma vez a mais do que o número existente. Aqui está uma implementação da função sucessor em C++20.

# 6. include <iostream> // Standard library for input and output
# 7. include <functional> // Standard library for std::function, used for higher-order functions

// Define a type alias `Church` that represents a Church numeral.
// A Church numeral is a higher-order function that takes a function f and returns another function.
using Church = std::function<std::function<int(int)>(std::function<int(int)>)>;

// Define the Church numeral for 0.
// `zero` is a lambda function that takes a function `f` and returns a lambda that takes an integer `x` and returns `x` unchanged.
// This is the definition of 0 in Church numerals, which means applying `f` zero times to `x`.
Church zero = [] \;,(auto f) {
 return [f] \;,(int x) { return x; }; // Return the identity function, applying `f` zero times.
};

// Define the successor function `succ` that increments a Church numeral by 1.
// `succ` is a lambda function that takes a Church numeral `n` (a number in Church encoding) and returns a new function.
// The new function applies `f` to the result of applying `n(f)` to `x`, effectively adding one more application of `f`.
Church succ = [] \;,(Church n) {
 return [n] \;,(auto f) {
 return [n, f] \;,(int x) {
 return f(n(f)(x)); // Apply `f` one more time than `n` does.
 };
 };
};

// Convert a Church numeral to a standard integer.
// `to_int` takes a Church numeral `n`, applies the function `[] \;,(int x) { return x + 1; }` to it,
// which acts like a successor function in the integer world, starting from 0.
int to_int(Church n) {
 return n([] \;,(int x) { return x + 1; })(0); // Start from 0 and apply `f` the number of times encoded by `n`.
}

int main() {
 // Create the Church numeral for 1 by applying `succ` to `zero`.
 auto one = succ(zero);

 // Create the Church numeral for 2 by applying `succ` to `one`.
 auto two = succ(one);

 // Output the integer representation of the Church numeral `two`.
 std::cout << _Sucessor de 1: _ << to_int(two) << std::endl;

 return 0; // End of program
}

Para finalizar podemos fazer uma implementação em python 3.x:

# Define the Church numeral for 0.
# `zero` is a function that takes a function `f` and returns another function that takes an argument `x` and simply returns `x`.
# This represents applying `f` zero times to `x`, which is the definition of 0 in Church numerals.
def zero(f):
 return lambda x: x # Return the identity function, applying `f` zero times.

# Define the successor function `succ` that increments a Church numeral by 1.
# `succ` is a function that takes a Church numeral `n` (a function) and returns a new function.
# This new function applies `f` one additional time to the result of `n(f)(x)`, effectively adding 1.
def succ(n):
 return lambda f: lambda x: f(n(f)(x)) # Apply `f` one more time than `n` does.

# Convert a Church numeral to a standard integer.
# `to_int` takes a Church numeral `church_n` and applies the function `lambda x: x + 1` to it,
# which mimics the successor function for integers, starting from 0.
def to_int(church_n):
 return church_n(lambda x: x + 1)(0) # Start from 0 and apply `f` the number of times encoded by `church_n`.

# Create the Church numeral for 1 by applying `succ` to `zero`.
one = succ(zero)

# Create the Church numeral for 2 by applying `succ` to `one`.
two = succ(one)

# Output the integer representation of the Church numeral `two`.
print(_Sucessor de 1:_, to_int(two)) # This will print 2, the successor of 1 in Church numerals.

Poderíamos refazer todas as operações em cálculo lambda que demonstramos anteriormente em cálculo lambda puro, contudo este não é o objetivo deste texto.

A representação dos números naturais no cálculo lambda mostra como um sistema simples de funções pode codificar estruturas matemáticas complexas. Essa representação nos permite uma visão sobre a natureza da computação e a expressividade de sistemas baseados em funções. Isso prova a universalidade do cálculo lambda, mostrando que ele pode representar funções e dados.

Complementarmente a representação dos números naturais no cálculo lambda serve de base para sistemas de tipos em linguagens de programação funcionais. Ela mostra como abstrações matemáticas podem ser codificadas em funções puras. Embora linguagens como Haskell não usem diretamente os números de Church, o conceito de representar dados como funções é essencial. Em Haskell, por exemplo, listas são manipuladas com funções de ordem superior que se parecem com os números de Church.

Os números de Church mostram como o cálculo lambda pode codificar dados complexos e operações usando exclusivamente funções. Eles dão uma base sólida para entender computação e abstração em linguagens de programação.

Questão de Prova: usando apenas cálculo lambda puro, reduza a função $(\lambda x.\; \lambda y.\; y\; (x\; x))\;(\lambda z.\; z + 1)\; 2$

Primeira Redução Beta, substituímos $x$ por $(\lambda z.\;z + 1)$ em $\lambda x.\;\lambda y.\;y\;(x\;x)$:

\[(\lambda x.\;\lambda y.\;y\;(x\;x))\;(\lambda z.\;z + 1) \rightarrow \lambda y.\;y\;((\lambda z.\;z + 1)\;(\lambda z.\;z + 1))\]

Reduzimos $(\lambda z.\;z + 1)\;(\lambda z.\;z + 1)$ Substituindo $z$ por $(\lambda z.\;z + 1)$ em $(z + 1)$:

\[(\lambda z.\;z + 1)\;(\lambda z.\;z + 1) \rightarrow (\lambda z.\;z + 1) + 1\] \[\rightarrow (\lambda w.\;w + 1) + 1\]

Então temos:

\[\lambda y.\;y\;((\lambda w.\;w + 1) + 1)\]

Segunda Redução Beta, aplicamos ao número 2:

\[(\lambda y.\;y\;((\lambda w.\;w + 1) + 1))\;2\] \[\rightarrow 2\;((\lambda w.\;w + 1) + 1)\]

A expressão continua em um processo infinito de adição de 1. Cada vez que tentamos avaliar $(\lambda w.\;w + 1)$, geramos outra função que adiciona 1, entrando em um loop infinito.

Podemos fazer novamente, considerando apenas o cálculo >lambda puro. Neste caso, teremos:

O termo inicial:

\[(\lambda x.\;\lambda y.\;y\;(x\;x))\;(\lambda z.\;z + 1)\;2\]

Deve ser reescrito substituindo as operações aritméticas por suas representações em cálculo lambda puro:

1. O número 2 como número de Church:

\[2 = \lambda f.\;\lambda x.\;f\;(f\;x)\]

1. O sucessor (substitui z + 1):

\[\text{succ} = \lambda n.\;\lambda f.\;\lambda x.\;f\;(n\;f\;x)\]

Então o termo se torna:

\[(\lambda x.\;\lambda y.\;y\;(x\;x))\;\text{succ}\;(\lambda f.\;\lambda x.\;f\;(f\;x))\]

Redução Beta, primeira Aplicação, substituímos $x$ por $\text{succ}$ em $\lambda x.\;\lambda y.\;y\;(x\;x)$:

\[(\lambda x.\;\lambda y.\;y\;(x\;x))\;\text{succ} \rightarrow \lambda y.\;y\;(\text{succ}\;\text{succ})\]

Redução Beta, segunda Aplicação, aplicamos ao número de Church 2:

\[(\lambda y.\;y\;(\text{succ}\;\text{succ}))\;(\lambda f.\;\lambda x.\;f\;(f\;x))\] \[\rightarrow (\lambda f.\;\lambda x.\;f\;(f\;x))\;(\text{succ}\;\text{succ})\]

Nos dois casos, o termo não possui forma normal beta. A redução continua indefinidamente devido à auto-aplicação do sucessor. Isto acontece porque $\text{succ}\;\text{succ}$ gera uma sequência infinita de aplicações quando usado como função em um número de Church.

7.2. Representação da Lógica Proposicional no Cálculo Lambda

O cálculo lambda oferece uma representação formal para lógica proposicional, similar aos números de Church para os números naturais. Neste cenário é possível codificar valores verdade e operações lógicas como termos lambda. Essa abordagem permite que operações booleanas sejam realizadas através de expressões funcionais.

Para entender o impacto desta representação podemos começar com os dois valores verdade, True (Verdadeiro) e False (Falso), que podem ser representados na forma de funções de ordem superior como:

Verdadeiro: $\text{True} = \lambda x. \lambda y.\;x$

Falso: $\text{False} = \lambda x. \lambda y.\;y$

Aqui, True é uma função que quando aplicada a dois argumentos, retorna o primeiro, enquanto False aplicada aos mesmos dois argumentos retornará o segundo. Tendo definido os termos para verdadeiro e falso, todas as operações lógicas podem ser construídas.

A esperta leitora deve concordar que é interessante, para nossos propósitos, começar definindo as operações estruturais da lógica proposicional: negação (NOT), conjunção (AND), disjunção (OR) e completar com a disjunção exclusiva (XOR) e a condicional (IF-THEN-ELSE).

7.2.1. Negação

A operação de negação, NOT ou $\lnot$ inverte o valor de uma proposição lógica atendendo a Tabela Verdade 19.1.1.A:

Tabela Verdade 19.1.1.A. Operação de negação.

Utilizando o cálculo lambda a operação de negação pode ser definida como a seguinte função de ordem superior nomeada:

A função $\text{Not}$ recebe um argumento booleano $b$ e se $b$ for True, $\text{Not}$ False; caso contrário, retorna True. Para ver isso acontecer com funções nomeadas podemos avaliar $\text{Not}\;\text{True}$:

A persistente leitora irá apreciar esta mesma avaliação sem usar qualquer função nomeada, ou seja cálculo lambda puro:

7.2.2. Conjunção

A operação de conjunção é uma operação binária que retorna True unicamente se ambos os operandos forem True obedecendo a Tabela Verdade 19.1.1.B.

Tabela Verdade 19.1.1.B. Operação conjunção.

No cálculo lambda, a operação de conjunção pode ser expresso por:

Vamos avaliar uma conjunção aplicada a dois verdadeiros, usando funções nomeadas $\text{And}\;\text{True}\;\text{False}$ passo a passo:

Esta aplicação fica mais simples se usarmos funções nomeadas:

A insistente leitora pode avaliar a conjunção usando unicamente o cálculo lambda puro, sem nenhuma função nomeada.

7.2.3. Disjunção

A operação de disjunção retorna True se pelo menos um dos operandos for True em obediência a Tabela Verdade 19.1.1.C.

Tabela Verdade 19.1.1.C. Operação disjunção.

Em cálculo lambda puro a operação de disjunção pode ser definida por:

Vamos avaliar $\text{Or}\;\text{True}\;\text{False}$ usando somente funções nomeadas:

Vamos refazer esta mesma aplicação, porém em cálculo lambda puro:

7.2.4. Disjunção Exclusiva

A operação Xor (ou disjunção exclusiva) retorna True se um, e somente um, dos operandos for True e obedece a Tabela Verdade 19.1.1.D.

Tabela Verdade 19.1.1.D. Operação disjunção exclusiva

Sua definição no cálculo lambda é dada por:

Para entender, podemos, novamente, avaliar $\text{Xor}\;\text{True}\;\text{False}$ usando funções nomeadas:

Para manter a tradição, vamos ver esta aplicação em cálculo lambda puro:

Questão de Prova 1: A operação $XNOR$ ($Not XOR$) retorna verdadeiro se as duas entradas forem iguais (ambas verdadeiras ou ambas falsas), e falso caso contrário. Crie uma função lambda que represente a operação $XNOR$ em cálculo lambda puro e aplique a $True$ e $False$.

Definições:

True: Representa a escolha do primeiro argumento.

\[\text{True} = \lambda x.\; \lambda y.\; x\]

False: Representa a escolha do segundo argumento.

\[\text{False} = \lambda x.\; \lambda y.\; y\]

Not: Inverte a entrada (de True para False e vice-versa).

\[\text{Not} = \lambda b.\; b\; \text{False}\; \text{True}\]

Xor: Retorna $True$ se uma e somente uma das entradas for $True$.

\[\text{Xor} = \lambda b.\; \lambda c.\; b\; (\text{Not}\; c)\; c\]

Agora que temos $True$, $False$, $Not$, e $XOR$, podemos definir $Not XOR$ ($XNOR$). Como $XNOR$ é o inverso de $XOR$, podemos usar a operação $Not$ aplicada ao resultado de $XOR$.

\[\text{XNOR} = \lambda b.\; \lambda c.\; (\text{Not}\; (\text{Xor}\; b\; c))\]

Em lambda puro precisaremos substitui r $XOR$ e $Not$ por suas definições lambda, para transformar tudo em uma expressão pura.

\[\text{XNOR} = \lambda b.\; \lambda c.\; (\lambda b.\; b\; \text{False}\; \text{True}) ((\lambda b.\; \lambda c.\; b\; (\lambda b.\; b\; \text{False}\; \text{True})\; c)\; b\; c)\]

Aplicação de $XNOR$ a $True$ e $False$

\[(\lambda b.\lambda c.(\lambda b.b(\lambda x.\lambda y.y)(\lambda x.\lambda y.x)) ((\lambda b.\lambda c.b(\lambda b.b(\lambda x.\lambda y.y)(\lambda x.\lambda y.x))c)bc)) (\lambda x.\lambda y.x)(\lambda x.\lambda y.y)\] \[(\lambda c.(\lambda b.b(\lambda x.\lambda y.y)(\lambda x.\lambda y.x)) ((\lambda b.\lambda c.b(\lambda b.b(\lambda x.\lambda y.y)(\lambda x.\lambda y.x))c) (\lambda x.\lambda y.x)c))(\lambda x.\lambda y.y)\] \[(\lambda b.b(\lambda x.\lambda y.y)(\lambda x.\lambda y.x)) ((\lambda b.\lambda c.b(\lambda b.b(\lambda x.\lambda y.y)(\lambda x.\lambda y.x))c) (\lambda x.\lambda y.x)(\lambda x.\lambda y.y))\] \[(\lambda b.b(\lambda x.\lambda y.y)(\lambda x.\lambda y.x))(\lambda x.\lambda y.x)\] \[\lambda x.\lambda y.y\]

O resultado é False ($\lambda x.\lambda y.y$), que é o valor esperado para XNOR True False.

7.2.5. Implicação, ou condicional

A operação implicação ou condicional, retorna True ou False, conforme a Tabela Verdade 19.1.1.E. A implicação é verdadeira quando a premissa é falsa ou quando tanto a premissa quanto a conclusão são verdadeiras.

Tabela Verdade 19.1.1.E. Operação de implicação.

A operação de implicação pode ser definida no cálculo lambda como:

Essa definição de implicação retorna False sempre que a premissa ($a$) é True e a conclusão ($b$) é False. Nos demais casos, retorna True.

Novamente podemos ver uma aplicação da implicação usando funções nomeadas:

E, ainda mantendo a tradição, vamos ver a mesma aplicação em cálculo lambda puro:

7.2.6. Operação IF-THEN-ELSE

A operação IF-THEN-ELSE não é uma das operações da lógica proposicional. IF-THEN-ELSE é, provavelmente, a mais popular estrutura de controle de fluxo em linguagens de programação. Em cálculo lambda podemos expressar esta operação por:

Nesta definição: $b$ representa a condição booleana (True ou False), $b$ representa o operador condicional do IF-THAN-ELSE. O $x$ representa o valor retornado se $b$ for True e $y$ representa o valor retornado se $b$ for False.

Vamos aplicar a estrutura condicional para a expressão em dois casos distintos:

1. Aplicação de IF-THEN-ELSE a True $x$ $y$

   \[\begin{align*} \text{IF-THEN-ELSE}\;\text{True}\;x\;y &= (\lambda b.\; \lambda x.\; \lambda y.\; b\; x\; y)\; (\lambda x.\; \lambda y.\; x)\; x\; y \\ \\ &\text{Substituímos $\text{True}$ e $\text{IF-THEN-ELSE}$ por suas definições em cálculo lambda:} \\ &= (\lambda b.\; \lambda x.\; \lambda y.\; b\; x\; y)\; (\lambda x.\; \lambda y.\; x)\; x\; y \\ \\ &\text{Aplicamos a primeira redução beta, substituindo $b$ por $\text{True}$ $(\lambda x.\; \lambda y.\; x)$:} \\ &\to_\beta (\lambda x.\; \lambda y.\; (\lambda x.\; \lambda y.\; x)\; x\; y) \\ \\ &\text{Aplicamos a segunda redução beta, aplicando $\text{True}$ $(\lambda x.\; \lambda y.\; x)$ ao argumento $x$:} \\ &\to_\beta (\lambda y.\; x) \\ \\ &\text{Finalmente, aplicamos a última redução beta, retornando $x$:} \\ &\to_\beta x \end{align*}\]

   Outra vez, para não perder o hábito, vamos ver esta mesma aplicação em Cálculo Lambda Puro:

   \[\begin{align*} \text{IF-THEN-ELSE}\;\text{True}\;x\;y &= (\lambda b.\; \lambda x.\; \lambda y.\; b\; x\; y)\; (\lambda x.\; \lambda y.\; x)\; x\; y \\ \\ &\text{Substituímos $\text{True}$ e $\text{IF-THEN-ELSE}$ por suas definições:} \\ &= (\lambda b.\; \lambda x.\; \lambda y.\; b\; x\; y)\; (\lambda x.\; \lambda y.\; x)\; x\; y \\ \\ &\text{Aplicamos a primeira redução beta, substituindo $b$ por $\text{True}$ $(\lambda x.\; \lambda y.\; x)$:} \\ &\to_\beta (\lambda x.\; \lambda y.\; (\lambda x.\; \lambda y.\; x)\; x\; y) \\ \\ &\text{Aplicamos a segunda redução beta, aplicando $\text{True}$ ao argumento $x$:} \\ &\to_\beta (\lambda y.\; x) \\ \\ &\text{Finalmente, aplicamos a última redução beta, retornando $x$:} \\ &\to_\beta x \end{align*}\]

2. Aplicação de IF-THEN-ELSE a False $x$ $y$

   \[\begin{align*} \text{IF-THEN-ELSE}\;\text{False}\;x\;y &= (\lambda b.\; \lambda x.\; \lambda y.\; b\; x\; y)\; (\lambda x.\; \lambda y.\; y)\; x\; y \\ \\ &\text{Substituímos $\text{False}$ e $\text{IF-THEN-ELSE}$ por suas definições em cálculo lambda:} \\ &= (\lambda b.\; \lambda x.\; \lambda y.\; b\; x\; y)\; (\lambda x.\; \lambda y.\; y)\; x\; y \\ \\ &\text{Aplicamos a primeira redução beta, substituindo $b$ por $\text{False}$ $(\lambda x.\; \lambda y.\; y)$:} \\ &\to_\beta (\lambda x.\; \lambda y.\; (\lambda x.\; \lambda y.\; y)\; x\; y) \\ \\ &\text{Aplicamos a segunda redução beta, aplicando $\text{False}$ $(\lambda x.\; \lambda y.\; y)$ ao argumento $y$:} \\ &\to_\beta (\lambda y.\; y) \\ \\ &\text{Finalmente, aplicamos a última redução beta, retornando $y$:} \\ &\to_\beta y \end{align*}\]

   Eu sei que a amável leitora não esperava por essa. Mas, eu vou refazer esta aplicação em cálculo lambda puro.

   \[\begin{align*} \text{IF-THEN-ELSE}\;\text{False}\;x\;y &= (\lambda b.\; \lambda x.\; \lambda y.\; b\; x\; y)\; (\lambda x.\; \lambda y.\; y)\; x\; y \\ \\ &\text{Substituímos $\text{False}$ e $\text{IF-THEN-ELSE}$ por suas definições:} \\ &= (\lambda b.\; \lambda x.\; \lambda y.\; b\; x\; y)\; (\lambda x.\; \lambda y.\; y)\; x\; y \\ \\ &\text{Aplicamos a primeira redução beta, substituindo $b$ por $\text{False}$ $(\lambda x.\; \lambda y.\; y)$:} \\ &\to_\beta (\lambda x.\; \lambda y.\; (\lambda x.\; \lambda y.\; y)\; x\; y) \\ \\ &\text{Aplicamos a segunda redução beta, aplicando $\text{False}$ ao argumento $y$:} \\ &\to_\beta (\lambda y.\; y) \\ \\ &\text{Finalmente, aplicamos a última redução beta, retornando $y$:} \\ &\to_\beta y \end{align*}\]

No cálculo lambda, o controle de fluxo é feito inteiramente através de funções e substituições. A estrutura IF-THEN-ELSE introduz decisões condicionais a este sistema lógico. Permitindo escolher entre dois resultados diferentes com base em uma condição booleana.

Afirmamos anteriormente que o cálculo lambda é um modelo de computação completo, capaz de expressar qualquer computação que uma máquina de Turing pode executar. Para alcançar essa completude, é necessário ser capaz de tomar decisões. A função IF-THEN-ELSE é uma forma direta de conseguir esta funcionalidade.

8. Estruturas de Dados Compostas

Embora o cálculo lambda puro não possua estruturas de dados nativas, podemos representá-las usando funções. Um exemplo clássico é a codificação de listas no estilo de Church, que nos permite aplicar recursão a essas estruturas.

Como a amável leitora deve lembrar, O cálculo lambda é um sistema formal para expressar computação baseada em abstração e aplicação de funções. Sendo Turing completo, o cálculo lambda pode expressar qualquer computação, ou estrutura de dados, realizável. Podemos representar estas estruturas usando funções. Esta seção explora como listas e tuplas são representadas e manipuladas no cálculo lambda puro.

Para nos mantermos na mesma linha de raciocínio, vamos lembrar que:

1. Listas: Representam coleções ordenadas de elementos, potencialmente infinitas.

2. Tuplas: Representam coleções finitas e heterogêneas de elementos. Nesta seção, tuplas representarão pares ordenados.

No cálculo lambda, estas estruturas são representadas usando funções de ordem superior. Por exemplo, uma lista $[1, 2, 3]$ em cálculo lambda puro é representada como:

Uma tupla $(3, 4)$ é representada como:

8.1. Listas

Para definirmos uma lista precisamos do conceito de lista vazia, que aqui será representado por $\text{nil}$ e uma função de construção de listas, $\text{cons}$:

1. Lista vazia ($\text{nil}$):

   \[\text{nil} = \lambda c.\,\lambda n.\;n\]

   Esta função ignora o primeiro argumento e retorna o segundo representando a lista vazia.

2. Construtor de lista ($\text{cons}$):

   \[\text{cons} = \lambda h. \lambda t. \lambda c. \, \lambda n.\;c\;h\;(t\;c\;n)\]

   O construtor recebe um elemento $h$ e uma lista $t\,$, e cria uma nova lista com $h$ na frente de $t\,$.

O termo $\text{cons}\,$ é, uma função de ordem superior e, como tal, não faz parte do cálculo lambda puro. Porém, facilita a visualização dos processos de aplicação e substituição e, consequentemente seu entendimento. Com $\text{nil}$ e $\text{cons}\,$, podemos criar e manipular listas. Por exemplo, a lista $[1, 2, 3]$ será representada como:

Esta lista está diagramada na Figura 20.1.B:

Figura 6.1.B: Diagrama de uma lista em cálculo lambda

Quando a leitora olha para o diagrama e para a função que representa a lista $[1,2,3]$ em cálculo lambda imagina que existe um abismo entre a sua ideia de lista e a função que encontramos. Não perca as esperanças, não é tão complicado quanto parece. Só trabalhoso. Chegamos a esta função começando com a lista vazia:

Adicionamos o elemento 3:

Após a redução-$beta\,$, temos:

Adicionamos o elemento 2:

Após a redução-$beta\,$, obtemos:

Finalmente, adicionamos o elemento 1:

Após a redução-$beta\,$, a representação final será:

Esta é a representação completa da lista $[1, 2, 3]$ em cálculo lambda puro. Esta representação permite operações recursivas sobre listas, como mapear funções ou calcular comprimentos. A curiosa leitora pode matar a curiosidade vendo a definição de uma de duas funções em cálculo lambda puro para lidar com listas:

8.1.1. Função Comprimento de lista (Length)

Vamos criar uma função para calcular o comprimento de uma lista usando o combinador $Y$:

Aqui, $\text{succ}$ é a função que retorna o sucessor de um número, e o corpo da função aplica-se recursivamente até que a lista seja esvaziada.

Exemplo 1: Vamos calcular o Comprimento da Lista $[1, 2, 3]$ em Cálculo Lambda Puro, usando $\text{length}$:

Definição de $\text{length}$:

Representação da lista $[1, 2, 3]$:

Aplicamos $\text{length}$ à lista:

O combinador $Y$ permite a recursão. Após aplicá-lo, obtemos:

Aplicamos a função à lista:

Reduzimos, aplicando $c$ e $n$:

Reduzimos cada aplicação de $(\lambda h. \lambda t. \text{succ}\;(\text{length}\;t))$:

Sabemos que $\text{length}\;\text{nil} = 0\,$, então:

Cada $\text{succ}$ incrementa o número por 1, então o resultado é 3.

Portanto, $\text{length}\;[1, 2, 3] = 3$ em cálculo lambda puro.

8.1.1.1. Função Soma (Sum) dos Elementos de uma Lista

Da mesma forma que fizemos com a função comprimento, podemos definir uma função para somar os elementos de uma lista:

Essa função percorre a lista somando os elementos, aplicando recursão via o combinador $Y$ até que a lista seja consumida.

Exemplo 1: Vamos aplicar esta função à lista $[1, 2, 3]$:

Representação da lista $[1, 2, 3]$:

Aplicamos $\text{sum}$ à lista:

O combinador $Y$ permite a recursão. Após aplicá-lo, obtemos:

Aplicamos a função à lista:

Reduzimos, aplicando $c$ e $n$:

Reduzimos cada aplicação de $(\lambda h. \lambda t. \text{add}\;h\;(\text{sum}\;t))$:

Sabemos que $\text{sum}\;\text{nil} = 0\,$, então:

Realizamos as adições de dentro para fora:

Portanto, $\text{sum}\;[1, 2, 3] = 6$ em cálculo lambda puro.

8.1.1.2. Funções Head e Tail em Cálculo Lambda Puro

As funções Head e Tail são funções uteis na manipulação de listas, principalmente em linguagens funcionais. Vamos definir estas funções em cálculo lambda puro. Começando pela função $\text{head}$:

Em seguida, temos a função $\text{tail}$:

Exemplo 1: Aplicação à lista [1, 2, 3]

Aplicação de Head: Aplicamos Head à lista:

Reduzimos:

Aplicamos $c$ e $n$:

Reduzimos:

Portanto, $\text{head}\;[1, 2, 3] = 1\,$.

Aplicação de Tail:

Seja o estado após a aplicação de $c$ e $n$:

Avaliamos de dentro para fora. Começando com a expressão mais interna:

Aplicando $h = 3$:

Aplicando $t = (\lambda x.\;x)$:

Agora a expressão intermediária:

Aplicando $h = 2$:

Aplicando $t = (\lambda x.\;x)$:

Por fim, a expressão mais externa:

Aplicando $h = 1$:

Aplicando $t = (\lambda x.\;x)$:

Após todas estas reduções, a lista resultante é construída usando o construtor de lista padrão:

Que representa a lista $[2, 3]$.

Listas são um tipo de dado composto útil para a maior parte das linguagens de programação. Não poderíamos deixar de definir listas em cálculo lambda puro para exemplificar a possibilidade da criação de algoritmos em cálculo lambda. Outra estrutura indispensável são as tuplas.

8.2. Tuplas em Cálculo Lambda Puro

Definimos uma tupla de dois elementos, que pode representar um par ordenado, como:

A tupla $(3,4)$ é representada assim:

Para que uma tupla seja útil, precisamos ser capazes de trabalhar com seus elementos individualmente. Para isso, podemos definir duas funções: $\text{first}$ e $\text{follow}\,$.

8.2.1. Função First

A função First retorna o primeiro elemento da tupla:

Exemplo: Aplicação a $(3,4)$:

Redução:

8.2.2. Função Last

A função Last retorna o último elemento da tupla:

Exemplo 2: Aplicação a $(3,4)$:

Redução:

Questão de Prova 1: usando cálculo lambda puro crie uma tupla para o par $(3,5)$ e aplique a ela as funções $first$ e $last$.

O par $(x, y)$ pode ser definido no cálculo lambda utilizando a seguinte expressão de pares de Church:

\[(x, y) = \lambda f.\;f\;x\;y\]

Queremos criar a tupla $(3, 5)$. Primeiro, precisamos representar os números $3$ e $5$ usando a notação lambda de números naturais (também conhecidos como números de Church).

Representação de $3$:

\[3 = \lambda s.\;\lambda z.\;s\;(s\;(s\;z))\]

Representação de $5$:

\[5 = \lambda s.\;\lambda z.\;s\;(s\;(s\;(s\;(s\;z))))\]

Agora podemos criar a tupla $(3, 5)$ usando a definição de pares:

\[\text{pair} = (\lambda f.\;f\;3\;5)\]

Funções first e last: as funções first e last são responsáveis por extrair o primeiro e o segundo elemento do par, respectivamente. Elas são definidas como:

first:

\[\text{first} = \lambda p.\;p\;(\lambda x.\;\lambda y.\;x)\]

last:

\[\text{last} = \lambda p.\;p\;(\lambda x.\;\lambda y.\;y)\]

Aplicação das Funções first e last à Tupla: vamos aplicar as funções first e last à tupla $(3, 5)$.

Para first, aplicamos a tupla à função que retorna o primeiro elemento:

\[\text{first}\;(\text{pair}) = (\lambda p.\;p\;(\lambda x.\;\lambda y.\;x))\;(\lambda f.\;f\;3\;5)\]

Para last, aplicamos a tupla à função que retorna o segundo elemento:

\[\text{last}\;(\text{pair}) = (\lambda p.\;p\;(\lambda x.\;\lambda y.\;y))\;(\lambda f.\;f\;3\;5)\]

Em resumo temos:

\[3 = \lambda s.\; \lambda z.\; s\; (s\; (s\; z))\] \[5 = \lambda s.\; \lambda z.\; s\; (s\; (s\; (s\; (s\; z))))\]

Criação da Tupla (3, 5):

\[\text{pair} = \lambda f.\; f\; 3\; 5\]

Função first e Aplicação à Tupla:

\[\text{first} = \lambda p.\; p\; (\lambda x.\; \lambda y.\; x)\] \[\text{first}\; (\text{pair}) = (\lambda p.\; p\; (\lambda x.\; \lambda y.\; x))\; (\lambda f.\; f\; 3\; 5)\]

Substituindo $\text{pair}$:

\[= (\lambda f.\; f\; 3\; 5)\; (\lambda x.\; \lambda y.\; x)\]

Aplicando a função:

\[= (\lambda x.\; \lambda y.\; x)\; 3\; 5\]

Avaliando a aplicação:

\[= 3\]

Função last e Aplicação à Tupla

\[\text{last} = \lambda p.\; p\; (\lambda x.\; \lambda y.\; y)\]

Aplicação:

\[\text{last}\; (\text{pair}) = (\lambda p.\; p\; (\lambda x.\; \lambda y.\; y))\; (\lambda f.\; f\; 3\; 5)\]

Substituindo $\text{pair}$:

\[= (\lambda f.\; f\; 3\; 5)\; (\lambda x.\; \lambda y.\; y)\]

Aplicando a função:

\[= (\lambda x.\; \lambda y.\; y)\; 3\; 5\]

Avaliando a aplicação:

\[= 5\]

9. Cálculo Lambda e Haskell

Haskell implementa diretamente conceitos do cálculo lambda. Vejamos alguns exemplos:

1. Funções Lambda: em Haskell, funções lambda são criadas usando a sintaxe \x -> …, que é análoga à notação $\lambda x.$ do cálculo lambda.

   -- Cálculo lambda: \lambda x.\;x
   identidade = \x -> x
   -- Cálculo lambda: \lambda x.\lambda y.x
   constante = \x -> \y -> x
   -- Uso:
   main = do
   print (identidade 5) -- Saída: 5
   print (constante 3 4) -- Saída: 3
   

2. Aplicação de Função: a aplicação de função em Haskell é semelhante ao cálculo lambda, usando justaposição:

   -- Cálculo lambda: (\lambda x.\;x+1)\;5
   incrementar = (\x -> x + 1)\;5
   main = print incrementar -- Saída: 6
   

3. currying: Haskell usa _currying_por padrão, permitindo aplicação parcial de funções:

   -- Função de dois argumentos
   soma :: Int -> Int -> Int
   soma x\;y = x + y
   -- Aplicação parcial
   incrementar :: Int -> Int
   incrementar = soma 1
   
   main = do
   print (soma 2 3) -- Saída: 5
   print (incrementar 4) -- Saída: 5
   

4. Funções de Ordem Superior: Haskell suporta funções de ordem superior, um dos conceitos do cálculo lambda:

   -- map é uma função de ordem superior
   dobrarLista :: [Int] -> [Int]
   dobrarLista = map (\x -> 2 * x)
   
   main = print (dobrarLista [1,2,3]) -- Saída: [2,4,6]
   

5. Codificação de Dados: no cálculo lambda puro, não existem tipos de dados primitivos além de funções. Haskell, sendo uma linguagem prática, fornece tipos de dados primitivos, mas ainda permite codificações similares às do cálculo lambda.

6. Booleanos: no cálculo lambda, os booleanos podem ser codificados como:

Em Haskell, podemos implementar isso como:

True :: a -> a -> a
True = \x -> \y -> x

False :: a -> a -> a
False = \x -> \y -> y

-- Função if-then-else
if' :: (a -> a -> a) -> a -> a -> a
if' b t e = b t e

main = do
   print (if' True _verdadeiro_ _falso_) -- Saída: _verdadeiro_
   print (if' False _verdadeiro_ _falso_) -- Saída: _falso_

1. Números Naturais: os números naturais podem ser representados usando a codificação de Church:

Em Haskell, teremos:

type Church a = (a -> a) -> a -> a

zero :: Church a
zero = \f -> \x -> x

succ' :: Church a -> Church a
succ' n = \f -> \x -> f (n f\;x)

one :: Church a
one = succ' zero

two :: Church a
two = succ' one
-- Converter para Int
toInt :: Church Int -> Int
toInt n = n (+1) 0
main = do
   print (toInt zero) -- Saída: 0
   print (toInt one) -- Saída: 1
   print (toInt two) -- Saída: 2

O cálculo lambda é a base teórica para as linguagens de programação que usam o paradigma da programação funcional, especialmente em Haskell. Mas, para isso, precisamos considerar os tipos.

10. Notas e Referências