Competitive Programming in C++ Insights - Introduction

Advanced optimization strategies for competitive programming in C++20 focus on using macros, lambdas, and templates to improve efficiency and minimize errors. Techniques like dynamic data manipulation and compile-time evaluation streamline coding for high-performance contests. By applying these methods, programmers can write cleaner, faster code, making complex algorithms easier to implement during competition.
C++ remains one of the most popular languages in competitive programming due to its performance, flexibility, and rich standard library. However, knowledge of efficient algorithms is as important,if not more so, than the programming language itself. Mastering efficient algorithms and optimized techniques is crucial for success in programming contests, where solving complex problems under strict time and memory constraints is the norm. in that same vein, understanding the nuances of algorithmic complexity can dramatically affect both performance and outcomes.
This work explores advanced algorithmic strategies, optimization techniques, and data structures that help tackle a wide range of computational challenges effectively. By optimizing input/output operations, leveraging modern C++ features, and utilizing efficient algorithms, we’ll see how to improve problem-solving skills in competitive programming. We’ll be pushing the boundaries of what can be achieved with minimal resources and tight constraints.
The scene of this particular whodunnit may seem unlikely, but input/output operations often become the hidden bottleneck in performance-critical applications. By default, C++ performs synchronized I/O with C’s standard I/O libraries, which can be slower. A simple trick to improve I/O speed is disabling this synchronization:
std::ios_base::sync_with_stdio(false);
cin.tie(nullptr);
This small change can make a significant difference when dealing with large input datasets. Throughout this guide, we will explore similar techniques, focusing on the efficient use of data structures like arrays and vectors, as well as modern C++20 features that streamline your code. You will learn how to apply optimizations that minimize overhead and effectively leverage STL containers and algorithms to boost both runtime performance and code readability. From handling large-scale data processing to optimizing solutions under tight time constraints, these strategies will prepare you to excel in programming contests.
Besides C++20, we will study the most efficient algorithms for each of the common problems found in competitions held by organizations like USACO and ICPC.
In this goal, processing large arrays or sequences quickly and efficiently is essential in competitive programming. Techniques in array manipulation are tailored to handle millions of operations with minimal overhead, maximizing performance. In graph algorithms, the focus shifts to implementing complex traversals and finding shortest paths, addressing problems from route optimization to network connectivity. These methods require precise control over nodes and edges, whether working with directed or undirected graphs.
String processing handles tasks like matching, parsing, and manipulating sequences of characters. It requires carefully crafted algorithms to search, replace, and transform strings, often using specialized data structures like suffix trees to maintain performance. Data structures go beyond basic types, introducing advanced forms such as segment trees and Fenwick trees. These are essential for managing and querying data ranges quickly, especially in scenarios where direct computation is too slow.
Computational geometry tackles geometric problems with high precision, calculating intersections, areas, and volumes. The focus is on solving spatial problems using algorithms that respect boundaries of precision and efficiency, delivering results where accuracy is crucial.
The journey through competitive programming in C++ starts with the basics. It’s not a journey we chose lightly. Ana Flávia Martins dos Santos, Isabella Vanderlinde Berkembrock, and Michele Cristina Otta inspired it. They succeeded without training. We wanted to build on that. Our goal is not only to present C++20 and a key set of algorithms for competitive programming, but also to inspire them, and everyone who reads this work or follows my courses, to become better professionals. We hope they master a wide range of computational tools that are rarely covered in traditional courses.
We’ll start with a set of small tricks and tips for typing and writing code to cut down the time spent drafting solutions. In many contests, it’s not enough for your code to be correct and fast; the time you spend presenting your solutions to the challenges matters too. So, typing less and typing fast is key.
For each problem type, we’ll study the possible algorithms, show the best one based on complexity, and give you a Python pseudocode followed by a full C++20 solution. We won’t fine-tune the Python code, but it runs and works as a solid base for competitive programming practice in Python. When needed, we’ll break down C++20 methods, functions, operators, and classes, often highlighting them for focus. There are clear, solid reasons why we picked C++20.
C++ is a powerful tool for competitive programming. It excels in areas like array manipulation, graph algorithms, string processing, advanced data structures, and computational geometry. Its speed and rich standard library make it ideal for creating efficient solutions in competitive scenarios.
We cover the essentials of looping, from simple for and while loops to modern C++20 techniques like range-based for loops with views and parallel execution policies. The guide also explores key optimizations: reducing typing overhead, leveraging the Standard Template Library (STL) effectively, and using memory-saving tools like std::span.
Mastering these C++20 techniques prepares you for a wide range of competitive programming challenges. Whether handling large datasets, solving complex problems, or optimizing for speed, these strategies will help you write fast, efficient code. This knowledge will sharpen your skills, improve your performance in competitions, and deepen your understanding of both C++ and algorithmic thinking—skills that go beyond the competition.
C++ shows its strength when solving complex problems. In array manipulation, it supports fast algorithms like binary search with $O(\log n)$ time complexity, crucial for quick queries in large datasets. For graph algorithms, C++ can implement structures like adjacency lists with a space complexity of $O(V + E)$, where $V$ is vertices and $E$ is edges, making it ideal for sparse graphs.
In string processing, C++ handles pattern searching efficiently, using algorithms like KMP (Knuth-Morris-Pratt), which runs in $O(n + m)$, where $n$ is the text length and $m$ is the pattern length. Advanced data structures, such as segment trees, allow for query and update operations in $O(\log n)$, essential for range queries and frequent updates.
C++ also handles computational geometry well. Algorithms like Graham’s scan find the convex hull with $O(n \log n)$ complexity, demonstrating C++’s efficiency in handling geometric problems.
We are going to cover a lot of ground. From basic techniques to advanced algorithms. But remember, it all started with Ana, Isabella, and Michele. Their success without training showed us what’s possible. Now, armed with these tools and knowledge, you’re ready to take on any challenge in competitive programming. The code is clean. The algorithms are efficient. The path is clear. Go forth and compete.
1.1 Time and Space Complexity
In this section, we’ll gona take a tour by time and space complexities, looking at how they affect algorithm efficiency, especially in competitive programming, without all mathematics. We’ll break down loops, recursive algorithms, and how different complexity classes shape performance. We’ll also look at space complexity and memory use, which matter when handling large datasets.
In this section, we’ll take a tour through time and space complexities, looking at how they affect algorithm efficiency, especially in competitive programming, without heavy mathematics. Before diving into specific examples, let’s visualize how different complexity classes grow with input size. Figure 1.1.A provides a clear picture of how various algorithmic complexities scale:
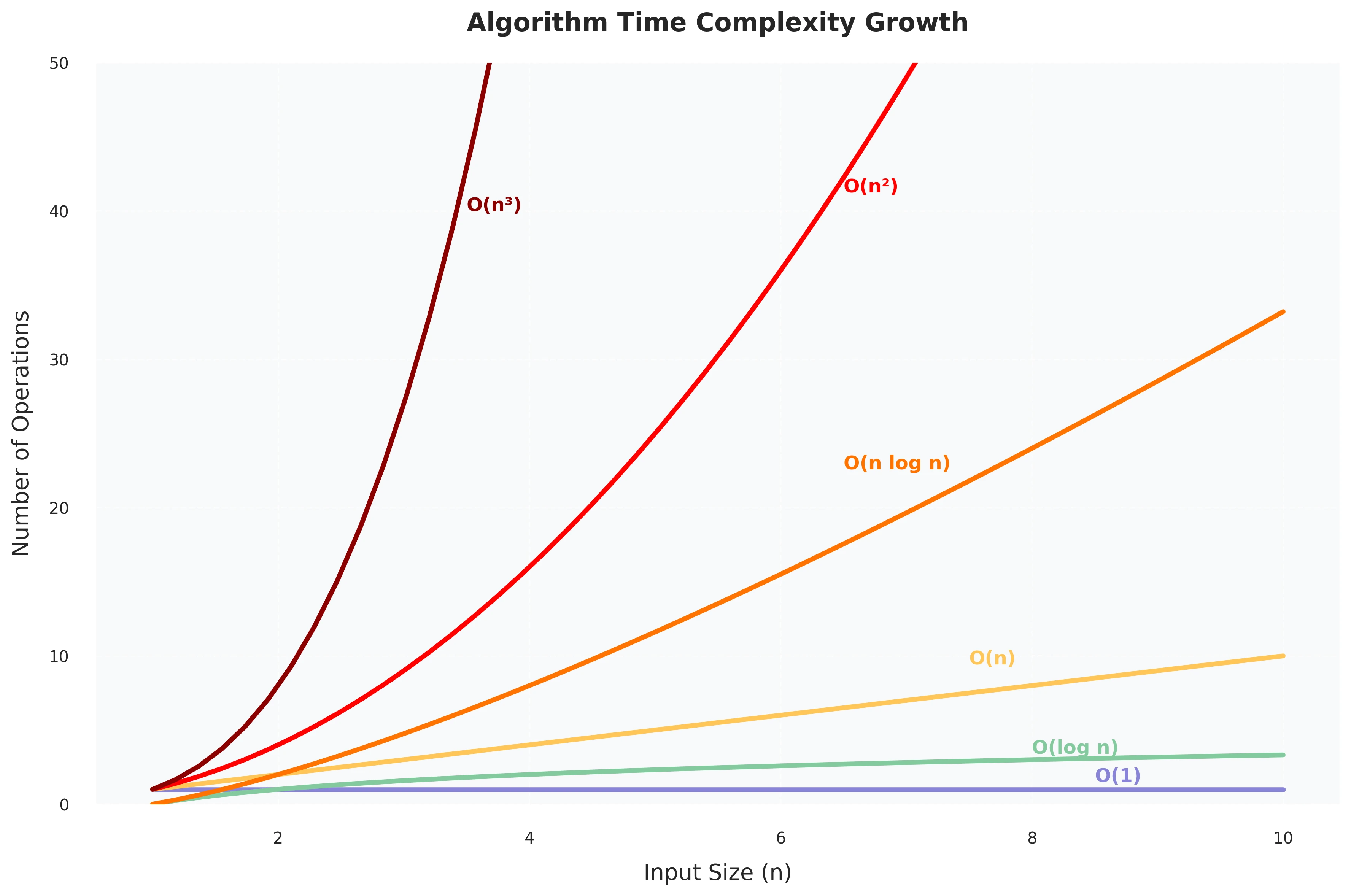
Figure 1.1.A: Growth comparison of common algorithmic complexities. The graph shows how the number of operations increases with input size for different complexity classes. Notice how O(1) remains constant, O(log n) grows very slowly, O(n) increases linearly, while O(n²) and O(n³) show dramatically steeper growth curves.
This visualization helps us understand why choosing the right algorithm matters. For small inputs, the differences might seem negligible, but as the input size grows, the impact becomes dramatic. A cubic algorithm (O(n³)) processing an input of size 10 performs 1,000 operations, while a linear algorithm (O(n)) only needs 10 operations for the same input. This difference becomes even more pronounced with larger inputs, making algorithm selection crucial for competitive programming, where both time and memory constraints are strict.
We’ll break down loops, recursive algorithms, and how different complexity classes shape performance. We’ll also look at space complexity and memory use, which matter when handling large datasets.
One major cause of slow algorithms is having multiple nested loops that run over the input data. The more nested loops there are, the slower the algorithm gets. With $k$ nested loops, the time complexity rises to $O(n^k)$. Alright, I lied. There is a little bit of math.
For instance, the time complexity of the following code fragment is $O(n)$:
for (int i = 1; i <= n; i++) {
// code
}
And the time complexity of the following code is $O(n^2)$ due to the nested loops:
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
// code
}
}
While time complexity gets most of the attention, space complexity is just as crucial, especially with large inputs. A loop like the one below has a time complexity of $O(n)$, but if it creates an array to store values, it also has a space complexity of $O(n)$:
std::vector<int> arr(n);
for (int i = 1; i <= n; i++) {
arr.push_back(i);
}
Don’t worry if you don’t know all the C++ syntax. I mean, I wish you did, but hey, we’ll get there. In competitive programming, excessive memory use can cause your program to exceed memory limits, though this isn’t very common in competitions. Always keep an eye on space complexity, especially when using arrays, matrices, or other data structures that grow with input size. Manage memory wisely to avoid crashes and penalties. And, there are penalties.
1.1.2. Order of Growth
Time complexity doesn’t show the exact number of times the code inside a loop runs; it shows how the runtime grows. In these examples, the loop runs $3n$, $n+5$, and $\lfloor n/2 \rfloor$ times, but all still have a time complexity of $O(n)$:
for (int i = 1; i <= 3*n; i++) {
// code
}
for (int i = 1; i <= n+5; i++) {
// code
}
for (int i = 1; i <= n; i += 2) {
// code
}
This is true because time complexity looks at growth, not exact counts. Big-O ignores constants and small terms since they don’t matter much as input size ($n$) gets large.
Here’s why each example still counts as $O(n)$:
-
$3n$ executions: The loop runs $3n$ times, but the constant $3$ doesn’t change the growth. It’s still linear, so it’s $O(n)$.
-
$n + 5$ executions: The $+5$ is just a fixed number. It’s small next to $n$ when things get big. The main growth is still $n$, so it’s $O(n)$.
-
$\lfloor n/2 \rfloor$ executions: Cutting $n$ in half or any fraction doesn’t change the overall growth rate. It’s still linear, so it’s $O(n)$.
Big-O isn’t disconnected from real execution speed. Constants like the $3$ in $3n$ do affect how fast the code runs, but they aren’t the focus of Big-O. In real terms, an algorithm with $3n$ operations will run slower than one with $n$, but both grow at the same rate—linearly. That’s why they both fall under $O(n)$ notation.
Big-O doesn’t ignore these factors because they don’t matter; it simplifies them. It’s all about the growth rate, not the exact count, because that’s what matters most when inputs get large.
Another example where time complexity is $O(n^2)$:
for (int i = 1; i <= n; i++) {
for (int j = i+1; j <= n; j++) {
// code
}
}
When an algorithm has consecutive phases, the overall time complexity is driven by the slowest phase. The phase with the highest complexity usually becomes the bottleneck. For example, the code below has three phases with time complexities of $O(n)$, $O(n^2)$, and $O(n)$. The slowest phase dominates, making the total time complexity $O(n^2)$:
for (int i = 1; i <= n; i++) {
// phase 1 code
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
// phase 2 code
}
}
for (int i = 1; i <= n; i++) {
// phase 3 code
}
When looking at algorithms with multiple phases, remember that each phase can also add to memory use. In the example above, if phase 2 creates an $n \times n$ matrix, the space complexity jumps to $O(n^2)$, matching the time complexity. Sometimes, time complexity depends on more than one factor. This means the formula includes multiple variables. For instance, the time complexity of the code below is $O(nm)$:
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// code
}
}
If the algorithm above uses a data structure like an $n \times m$ matrix, the space complexity also becomes $O(n\times m)$. This increases memory usage, especially with large inputs.
The time complexity of a recursive function depends on how often it’s called and the complexity of each call. To understand this better, let’s look at a progression of recursive functions, from simple to complex:
-
Linear Recursion - Simple Countdown:
void countdown(int n) { if (n == 0) return; std::cout << n << " "; countdown(n-1); }This function makes $n$ calls, each doing $O(1)$ work, resulting in $O(n)$ complexity. It’s a straightforward example where each call leads to exactly one recursive call. Let’s see it a little bit more careful: Here, each call to the function creates exactly one more call, until n = 0. The Table 1.1.A shows the calls made from a single initial call to countdown(n):
Function Call Number of Calls countdown(n) 1 countdown(n-1) 1 countdown(n-2) 1 … … countdown(1) 1 Table 1.1.A - Counting calls in linear recursion.
So, the total time complexity is:
\[1 + 1 + 1 + \cdots + 1 = n = O(n)\] -
Tail Recursion with Accumulator:
int sum_to_n(int n, int acc = 0) { if (n == 0) return acc; return sum_to_n(n-1, acc + n); }The accumulator doesn’t affect the number of calls. Each call creates one recursive call until $n = 0$. The Table 1.1.B shows the pattern:
Function Call Number of Calls Accumulator Value sum_to_n(n, 0) 1 0 sum_to_n(n-1, n) 1 n sum_to_n(n-2, n+(n-1)) 1 n+(n-1) … … … sum_to_n(1, partial) 1 partial Table 1.1.B - Analyzing tail recursion with accumulator.
The total time complexity is:
\[1 + 1 + 1 + \cdots + 1 = n = O(n)\] -
Binary Recursion - Generating Paths:
binary_paths(int n, std::string path = "") { if (n == 0) { std::cout << path << "\n"; return; } binary_paths(n-1, path + "0"); binary_paths(n-1, path + "1"); }Each call creates two new calls, doubling at each level until $n = 0$. The Table 1.1.C shows this exponential growth:
Function Call Number of Calls Paths Generated binary_paths(n) 1 Root binary_paths(n-1) 2 “0”, “1” binary_paths(n-2) 4 “00”,”01”,”10”,”11” … … … binary_paths(0) 2^n All binary strings Table 1.1.C - Analyzing binary recursive growth.
The total time complexity is:
\[1 + 2 + 4 + \cdots + 2^n = 2^{n+1} - 1 = O(2^n)\] -
Multiple Recursion - Tribonacci Sequence:
tribonacci(int n) { if (n <= 1) return 0; if (n == 2) return 1; return tribonacci(n-1) + tribonacci(n-2) + tribonacci(n-3); // First numbers: 0, 0, 1, 1, 2, 4, 7, 13, 24, 44... // Each number is the sum of the previous 3 numbers }Each call spawns three recursive calls until the base cases. The Table 1.1.D shows the exponential growth:
Function Call Number of Calls Total New Calls tribonacci(n) 1 3 tribonacci(n-1) 3 9 tribonacci(n-2) 9 27 … … … tribonacci(≤2) 3^{n-2} Base cases Table 1.1.D - Analyzing three-way recursive growth.
The total time complexity is:
\[1 + 3 + 9 + \cdots + 3^{n-2} = \frac{3^{n-1} - 1}{2} = O(3^n)\]
These examples illustrate how recursive patterns affect complexity: Single recursion typically leads to linear complexity $O(n)$; Binary recursion often results in exponential complexity $O(2^n)$ e Multiple recursion can lead to even higher exponential complexity $O(k^n)$, where k is the number of recursive calls
Recursive functions also bring space complexity issues. Each call adds to the call stack, and with deep recursion, like this exponential example, the space complexity can be $O(n)$. Be aware that recursion depth is limited by the call stack’s size. In C++ and Java, the call stack has a fixed size determined by the system or runtime settings. If too many recursive calls occur, the stack can overflow, causing the program to terminate. Modern C++ compilers like GCC, Clang and MSVC can optimize tail-recursive calls through tail-call optimization (TCO), but this is not guaranteed and is generally not implemented in Java. In Python, recursion also has a limit, but it is managed differently. Python raises a RecursionError when the recursion depth exceeds a preset limit (default is $1,000$ calls). This exception can be caught, providing a safer way to handle deep recursion. However, adjusting the recursion limit with sys.setrecursionlimit() in Python can still lead to a stack overflow if set too high, as Python’s call stack size remains fixed. Unlike C++ and Java, Python does not support TCO, making deep recursion slower and more memory-intensive.
1.1.3. Common Complexity Classes
Here is a Table 1.1.E of common time complexities of algorithms:
| Complexity | Description | Examples |
|---|---|---|
| $O(1)$ | Constant time; the execution time remains the same regardless of input size. | Accessing an array element, hash lookups. |
| $O(\log n)$ | Logarithmic time; the input size is reduced by half in each step. | Binary search, finding largest power of $2$. |
| $O(\sqrt{n})$ | Sub-linear but slower than $O(\log n)$; often arises in problems where input is reduced by its square root. | Trial division for prime checking. |
| $O(n)$ | Linear time; the algorithm processes each element once. | Single loop over an array, linear search. |
| $O(n \log n)$ | Log-linear time; typical of algorithms that involve sorting or divide-and-conquer strategies. | Mergesort, heapsort, Fast Fourier Transform. |
| $O(n^2)$ | Quadratic time; usually involves two nested loops, processing pairs of elements. | Bubble sort, matrix multiplication (naive). |
| $O(n^3)$ | Cubic time; involves three nested loops, processing triples of elements. | Floyd-Warshall algorithm, matrix chain multiplication. |
| $O(2^n)$ | Exponential growth; common in recursive algorithms that explore all subsets or configurations. | Recursive subset generation, solving the Traveling Salesman Problem (TSP) recursively. |
| $O(n!)$ | Factorial time; often seen in algorithms that generate all possible permutations of input. | Permutation generation, brute-force TSP. |
Table 1.1.E - Common time complexities of algorithms.
The following text offers a more comprehensive explanation of each complexity listed in the table, recognizing that each of us may understand these concepts in different ways. You might find it helpful to keep both the table and the text on hand for reference.
$O(1)$ - Algorithms with constant time complexity execute in the same amount of time, regardless of input size. No matter how large or small the input is, the execution time remains unchanged. Examples include accessing an element in an array by its index or checking if a number is even. Constant-time operations are optimal for performance, making them desirable in many algorithmic designs.
$O(\log n)$ - Algorithms with logarithmic time complexity increase their runtime logarithmically as the input size grows. This typically occurs in divide-and-conquer algorithms, where the problem size is halved at each step. An example is binary search, where a sorted array is repeatedly divided in half until the target element is found. As input size increases, the runtime grows slowly, making logarithmic algorithms highly efficient for large inputs.
$O(\sqrt{n})$ - $O(\sqrt{n})$ algorithms reduce the input by its square root at each step, which is slower than logarithmic complexity but faster than linear complexity. This complexity often arises in specific mathematical algorithms, such as trial division for prime checking, where the factors are tested up to the square root of the number. It is efficient for certain computational problems but less common than other complexities.
$O(n)$ - $O(n)$ algorithms process each element of the input once, making the runtime proportional to the input size. Examples include linear search through an unsorted array or iterating through a list to calculate its sum. Linear algorithms are generally efficient for moderate input sizes but may become slow as input size grows significantly.
$O(n \log n)$ - $O(n \log n)$ algorithms have a runtime that grows in proportion to the input size multiplied by the logarithm of the input size. This complexity is common in efficient sorting algorithms like mergesort and heapsort, which combine linear processing with logarithmic division of input. It strikes a balance between scalability and efficiency, making it a standard choice for practical sorting and divide-and-conquer problems.
$O(n^2)$ - $O(n^2)$ algorithms have a runtime that grows quadratically as the input size increases, often due to two nested loops processing pairs of elements. Examples include bubble sort, insertion sort, and naive matrix multiplication. As the input size increases, the runtime grows significantly, making quadratic algorithms inefficient for large inputs.
$O(n^3)$ - $O(n^3)$ algorithms involve three nested loops and are often found in problems that require processing triples of elements. For example, the Floyd-Warshall algorithm for finding shortest paths in a graph has cubic complexity. Similar to quadratic algorithms, cubic ones become inefficient as input size increases, but they are sometimes unavoidable in certain computations.
$O(2^n)$ - $O(2^n)$ algorithms experience exponential growth in runtime as the input size increases, doubling with each additional input element. These algorithms often involve exploring all possible solutions, as seen in recursive solutions to problems like the Traveling Salesman Problem or generating all subsets of a set. Exponential algorithms become impractical for even moderately large inputs due to rapid increases in runtime.
$O(n!)$ - $O(n!)$ algorithms generate all possible permutations of the input, resulting in extremely high runtimes. This complexity is common in brute-force solutions to problems like permutation generation or the Traveling Salesman Problem. Factorial algorithms are the least efficient, with runtime growing rapidly even for small input sizes, making them unsuitable for large-scale computation.
Now that we’ve explored different time complexities, it’s useful to think about how they translate to actual performance. The next section will help you estimate whether an algorithm will be fast enough, based on input size and typical competition constraints.
1.1.4. Estimating Efficiency
Now that we’ve explored different time complexities, it’s useful to think about how they translate to actual performance. A modern Intel i7 processor can handle around $10^9$ operations per second. The next section will help you estimate whether an algorithm will be fast enough, based on input size and typical competition constraints. For instance, if an algorithm with $O(n^2)$ complexity requires $10^{10}$ operations, it would take roughly 10 seconds to run, which is too slow for most programming competitions 1.
You can also judge what time complexity you need based on the input size. Here’s a quick guide, assuming a one-second time limit, very common for C++ competitions:
| Input Size | Required Time Complexity |
|---|---|
| $n \leq 10$ | $O(n!)$ |
| $n \leq 20$ | $O(2^n)$ |
| $n \leq 500$ | $O(n^3)$ |
| $n \leq 5000$ | $O(n^2)$ |
| $n \leq 10^6$ | $O(n \log n)$ or $O(n)$ |
| $n$ is large | $O(1)$ or $O(\log n)$ |
Table 1.1.F - Theoretical relationship between time complexity and input size.
So, if your input size is $n = 10^5$, you’ll probably need an algorithm with $O(n)$ or $O(n \log n)$ time complexity. This helps you steer clear of approaches that are too slow.
Remember, time complexity is an estimate; it hides constant factors. An $O(n)$ algorithm could do $n/2$ or $5n$ operations, and these constants can change the actual performance.
1.2. Typing Better, Faster, Less
This section gives you practical steps to improve your speed and performance in competitive programming with C++20. C++ is fast and powerful, but using it well takes skill and focus. We will cover how to type faster, write cleaner code, and manage complexity. The goal is to help you code quicker, make fewer mistakes, and keep your solutions running fast.
Typing matters. The faster you type, the more time you save. Accuracy also counts, mistakes slow you down. Next, we cut down on code size without losing what’s important. Using tools like the Standard Template Library (STL), you can write less code and keep it clean. This is about direct, simple code that does the job right.
In this section, we won’t confine ourselves to general tricks. We will explore certain nuances and techniques specific to C++20, particularly those related to typing efficiency. Undoubtedly, in other chapters and sections, we will return to these same topics, but from different angles.From this point forward, the idea of clean and well-structured code will be left behind.
1.2.1. Typing Tips
If you don’t type quickly, you should invest at least two hours per week on the website: https://www.speedcoder.net. Once you have completed the basic course, select the C++ lessons and practice regularly. Time is crucial in competitive programming, and slow typing can be disastrous.
To expand on this, efficient typing isn’t just about speed; it’s about reducing errors and maintaining a steady flow of code. When you’re in a competitive programming, every second matters. Correcting frequent typos or having to look at your keyboard will significantly slow down your progress. Touch typing—knowing the layout of the keyboard and typing without looking—becomes a vital skill.
In a typical competitive programming contest, you have to solve several, typically $12$ or $15$, problems within a set time, about five hours. Typing fast lets you spend more time solving problems instead of struggling to get the code in. But speed means nothing without accuracy. Accurate and fast typing ensures that once you know the solution, you can code it quickly and correctly. Aim for a typing speed of at least 60 words per minute with high accuracy. Websites like https://www.speedcoder.net let you practice typing code syntax, which helps more than regular typing lessons. Besides it, learning specific shortcuts in C++ or Python boosts your speed in real coding situations. There are a simple equation for that:
\[\text{Time spent fixing errors } + \text{Time lost from slow typing }\] \[= \text{Lower overall performance in competitive programming}\]To keep improving your typing in competitive programming, start by using IDE shortcuts. Learn the keyboard shortcuts for your preferred Integrated Development Environment (IDE). Those shortcuts help you navigate and edit code faster, cutting down the time spent moving between the keyboard and mouse. In ICPC contests, the available IDE’s are, usually, Eclipse or VsCode, so knowing its shortcuts can boost your efficiency. Always check which IDE will be used in each competition since this may vary. And use it daily while training.
While typing, focus on frequent patterns in your code. Practice typing common elements like loops, if-else conditions, and function declarations. Embedding these patterns into your muscle memory saves time during contests. The faster you can type these basic structures, the quicker you can move on to solving the actual problem.
To succeed in a C++ programming competition, your first challenge is to type the following code fragment in under two minutes. If you can’t, don’t give up. Just keep practicing. To be the best in the world at anything, no matter what it is, the only secret is to train and train some more.
#include <iostream>
#include <vector>
#include <span>
#include <string>
#include <algorithm>
#include <random>
// Type aliases
using VI = std::vector<int>;
using IS = std::span<int>;
using STR = std::string;
// Function to double each element in the vector
void processVector(VI& vec) {
std::cout << "Processing vector...\n";
for (int i = 0; i < vec.size(); ++i) {
vec[i] *= 2;
}
}
// Function to display elements of a span
void displaySpan(IS sp) {
std::cout << "Displaying span: ";
for (const auto& elem : sp) {
std::cout << elem << " ";
}
std::cout << "\n";
}
int main() {
VI numbers;
STR input;
// Input loop: collect numbers from user
std::cout << "Enter integers (type 'done' when finished):\n";
while (true) {
std::cin >> input;
if (input == "done") break;
numbers.push_back(std::stoi(input));
}
// Process and display the vector
processVector(numbers);
std::cout << "Processed vector:\n";
int index = 0;
while (index < numbers.size()) {
std::cout << numbers[index] << " ";
++index;
}
std::cout << "\n";
// Shuffle the vector using a random number generator
std::random_device rd;
std::mt19937 gen(rd());
std::shuffle(numbers.begin(), numbers.end(), gen);
std::cout << "Shuffled vector:\n";
for (const auto& num : numbers) {
std::cout << num << " ";
}
std::cout << "\n";
// Display a span of the first 5 elements (if available)
if (numbers.size() >= 5) {
IS numberSpan(numbers.data(), 5);
displaySpan(numberSpan);
}
// Calculate sum of elements at even indices
int sum = 0;
for (int i = 0; i < numbers.size(); i += 2) {
sum += numbers[i];
}
std::cout << "Sum of elements at even indices: " << sum << "\n";
return 0;
}
Code Fragment 1.2.A - Code for self-assessment of your typing speed.
Don’t give up before trying. If you feel your typing speed isn’t enough, don’t stop here. Keep practicing. With each new algorithm, copy it and practice again until typing between $60$ and $80$ words per minute with an accuracy above $95%$ feels natural.
1.2.2. Typing Less in Competitive Programming
In competitive programming, time is a critical resource, and C++ is a language where you have to type a lot… like, seriously a lot. If anyone finds out I said that, I’ll have to deny it completely, it’s part of the C++ survival code! Therefore, optimizing typing speed and avoiding repetitive code can make a significant difference. Below, we will discuss strategies to minimize typing when working with std::vector during competitive programmings, where access to the internet or pre-prepared code snippets may be restricted.
1.2.2.1. Abbreviations
It may not be the cleanest approach, but the first thing that comes to mind… We can use #define to create short aliases for common vector types. This is particularly useful when you need to declare multiple vectors throughout the code.
#define VI std::vector<int>
#define VVI std::vector<std::vector<int>>
#define VS std::vector<std::string>
With these definitions, declaring vectors becomes much faster:
VI numbers; // std::vector<int> numbers;
VVI matrix; // std::vector<std::vector<int>> matrix;
VS words; // std::vector<std::string> words;
In this book, I’ll use a lot of comments to explain concepts, code, or algorithms. You, on the other hand, won’t use any comments. Not during training, and definitely not during competitions. If you even think about using one, seek professional advice. There are plenty of psychiatrists available online.
In C++, you can use
#defineto create macros and short aliases. Macros can define constants or functions at the preprocessor level. Macros can cause problems. They ignore scopes and can lead to unexpected behavior. So, For functions, macros can be unsafe. They don’t respect types or scopes.// Macro function #define SQUARE(x) ((x) * (x)) // Template function template<typename T> constexpr T square(T x) { return x * x; }Macros are processed before compilation. This makes debugging hard. The compiler doesn’t see macros the same way it sees code. With modern C++, you have better tools that the compiler understands. C++20 offers features like
constexprfunctions, inline variables, and templates. These replace most uses of macros. They provide type safety and respect scopes. They make code easier to read and maintain. You can define aconstexprfunction to compute the square of a number:constexpr int square(int n) { return n * n; }If you call
square(5)in a context requiring a constant expression, the compiler evaluates it at compile time.In summary, avoid macros when you can. Use modern C++20 features instead. They make your code safer and clearer.C++20 offers features like constexpr functions, inline variables, and templates. These replace most uses of macros. They provide type safety and respect scopes. They make code easier to read and maintain. You can define a constexpr function to compute the square of a number:
constexpr int square(int n) { return n * n; }If you call
square(5)in a context requiring a constant expression, the compiler evaluates it at compile time. Let’s explore how to use these features effectively, starting with basic constants and progressing to advanced compile-time computations:
- Basic Constant Declaration:
// Old way using macros (avoid) #define MAX_SIZE 100 // Modern way using const const int MAX_SIZE = 100;
- Simple Compiler-time Computation
// Basic constexpr function constexpr int square(int x) { return x * x; } // Usage: constexpr int result = square(5); // Computed at compile-time
- Conditional Compile-time Logic:
/// constexpr with conditionals constexpr int max(int a, int b) { return (a > b) ? a : b; } // This enables compile-time decision making constexpr int larger = max(10, 20); // Evaluates to 20 at compile-time
- Recursive Compile-time Computation:
// Recursive constexpr function constexpr int factorial(int n) { return (n <= 1) ? 1 : n * factorial(n-1); } // The entire recursion happens at compile-time constexpr int fact5 = factorial(5); // Evaluates to 120 at compile-time
- Generic Compile-time Computation:
// Template constexpr combining generics and compile-time evaluation template<typename T> constexpr T power(T base, int exp) { if (exp == 0) return 1;> if (exp == 1) return base; return base * power(base, exp-1); } // Works with different types, all at compile-time constexpr int int_power = power(2, 3); // 8 constexpr double dbl_power = power(2.5, 2); // 6.25In competitive programming, constexpr can be an advantage or disadvantage. It optimizes code by computing results at compile time, saving processing time during execution. If certain values are constant, you can precompute them with constexpr. However, many problems have dynamic input provided at runtime, where constexpr cannot help since it cannot compute values that depend on runtime input. Overall, constexpr is valuable when dealing with static data or fixed input sizes. But in typical ICPC-style competitions, you use it less often because most problems require processing dynamic input.
A smart way to reduce typing time is by using using to create abbreviations for frequently used vector types.
In many cases, the use of #define can be replaced with more modern and safe C++ constructs like using, typedef, or constexpr. The old #define does not respect scoping rules and does not offer type checking, which can lead to unintended behavior. Using typedef or using provides better type safety and integrates smoothly with the C++ type system, making the code more predictable and easier to debug.
For example:
#define VI std::vector<int>
#define VVI std::vector<std::vector<int>>
#define VS std::vector<std::string>
Can be replaced with using or typedef to create type aliases:
using VI = std::vector<int>;
using VVI = std::vector<std::vector<int>>;
using VS = std::vector<std::string>;
// Or using typedef (more common in C++98/C++03)
typedef std::vector<int> VI;
typedef std::vector<std::vector<int>> VVI;
typedef std::vector<std::string> VS;
using and typedef are preferred because they respect C++ scoping rules and offer better support for debugging, making the code more secure and readable. nevertheless, there are moments when we need a constant function.
In C++20, the use of
usingoffers significant advantages over the traditionaltypedef. The syntax ofusingis clearer, especially when defining complex types like pointers, templates, and function types. For instance,using FuncPtr = void(*)(int);is more readable thantypedef void(*FuncPtr)(int);, as the type definition aligns more closely with the general C++ syntax. Additionally,usingallows for creating aliases for templates, which is not possible withtypedef. This makes defining template-dependent types more flexible and straightforward, simplifying alias creation liketemplate<typename T> using Vec = std::vector<T>;, enhancing code reusability.Another benefit of
usingis that it aligns well with other modern language constructs, such asusing namespace, bringing greater consistency to modern C++ code. This helps maintain clarity in longer and more complex type definitions, making the code easier to read and maintain. Therefore, in C++20 projects, it is advisable to adoptusingfor type definitions, ensuring cleaner and more flexible code.
Nevertheless, if you have macros that perform calculations, you can replace them with constexpr functions:
#define SQUARE(x) ((x) * (x))
Can be replaced with:
constexpr int square(int x) {
return x * x;
}
constexpr functions provide type safety, avoid unexpected side effects, and allow the compiler to evaluate the expression at compile-time, resulting in more efficient and safer code.
In competitive programming, you might think using #define is the fastest way to type less and code faster. But typedef or using are usually more efficient. They avoid issues with macros and integrate better with the compiler. While reducing variable names or abbreviating functions might save time in a contest, remember that in professional code, clarity and maintainability are more important than typing speed. So avoid using shortened names and unsafe constructs like #define in production code, libraries, or larger projects.
In C++, you can create aliases for types. This makes your code cleaner. You use
typedeforusingto do this.using ull = unsigned long long;Now,
ullis an alias forunsigned long long. You can use it like this:ull bigNum = 123456789012345ULL;Numbers need type-specific suffixes like
ULL. When you writeull bigNumber = 123456789012345ULL;, theULLtells the compiler the number is anunsigned long long. Without it, the compiler might assume a smaller type likeintorlong, which can’t handle large values. This leads to errors and bugs. The suffix forces the right type, avoiding overflow and keeping your numbers safe. It’s a simple step but crucial. The right suffix means the right size, no surprises.In C++, suffixes are also used with floating-point numbers to specify their exact type. The suffix
fdesignates afloat, while no suffix indicates adouble, andlorLindicates along double. By default, the compiler assumesdoubleif no suffix is provided. Using these suffixes is important when you need specific control over the type, such as saving memory withfloator gaining extra precision withlong double. The suffix ensures that the number is treated correctly according to your needs.Exact type, exact behavior.
The rule is: know your numbers, suffix your numbers, and be happy.
1.2.2.2. Predefining Common Operations
If you know that certain operations, such as sorting or summing elements, are frequent in a competitive programming or in the algorithm you are going to code, consider defining these operations at the beginning of the code. The only real reason to use a macro in competitive programming is to predefine functions. For example:
#include <vector>
#include <algorithm>
// Alias for integer vector
using VI = std::vector<int>;
// Alias for the full range of the vector
#define ALL(vec) vec.begin(), vec.end()
// Function to sort the vector using constexpr
constexpr auto sVec = [](VI& vec) {
std::sort(vec.begin(), vec.end());
};
// Usage:
VI vec = {5, 3, 8, 1};
sVec(vec); // Sorts the vector using the lambda function
// Alternatively, you can still use ALL to simplify the sort:
std::sort(ALL(vec)); // Another way to sort the vector
Code Fragment 1.2.B: Example of using and constexpr to reduce typing time.
Keeping the macro #define ALL(vec) vec.begin(), vec.end() wasn’t madness, it was the competitive programming bug. The C++20 code needed to replace this macro with modern structures requires a lot of typing.
template<typename T>
constexpr auto all(T& container) {
return std::make_pair(container.begin(), container.end());
}
VI vec = {5, 3, 8, 1};
sort_vector(vec); // Sorts the vector using the lambda
std::sort(all(vec).first, all(vec).second); // Another way to sort using the utility function
In C++,
#includebrings code from libraries into your program. It lets you use functions and classes defined elsewhere. The line#include <vector>includes the vector library.Vectors are dynamic arrays. They can change size at runtime. You can add or remove elements as needed. We will know more about vectors and the vector library soon. In early code fragments we saw some examples of vector initialization. We will travel down this road soon.
The line
#include <algorithm>includes the algorithm library. It provides functions to work with data structures. You can sort, search, and manipulate collections.We can merge
<vector>and<algorithm>for efficient data processing. We’ve seen this in previous code examples where we used competitive programming techniques. Without competitive programming tricks and hacks, the libraries can be combined like this:#include <vector> #include <algorithm> #include <iostream> int main() { std::vector<int> numbers = {4, 2, 5, 1, 3}; std::sort(numbers.begin(), numbers.end()); for (int num : numbers) { std::cout << num << " "; } return 0; }Code 1.2.B: Simple and small program to print a vector
The program in Code 1.2.B, a simple example of professional code, sorts the numbers and prints:
1 2 3 4 5
Summing the values contained in a vector, or anther container, is a common problem in competitive programming. For these cases, C++20 offers std::accumulate. In C++, std::accumulate is part of the <numeric> library and calculates the sum (or other operations) over a range of elements starting from an initial value. Unlike other languages, C++ does not have a built-in sum function, but std::accumulate serves that purpose. As we can see in the provided fragment:
#define ALL(x) x.begin(), x.end() //that macro again
\\...
int sum_vector(const VI& vec) {
return std::accumulate(ALL(vec), 0);
}
The code std::accumulate(ALL(vec), 0); will be replaced in compilation time for std::accumulate(vec.begin(), vec.end(), 0) witch takes three arguments: the first two define the range to sum (vec.begin() to vec.end()); the third argument is the initial value, which is $0$, added to the summation result. If std::accumulate is used without a custom function, it defaults to addition, behaving like a simple summation. To calculate the sum of a vector’s elements:
std::accumulateuses functions to operate on elements. These functions are straightforward. They take two values and return one. Let’s see how they work.We can begin for Lambda functions, they are unnamed functions, useful for quick operations.
[](int a, int b) { return a + b; }This lambda adds two numbers. The
[]is called the capture list, which specifies which variables from the surrounding scope can be accessed inside the lambda. In this case, it’s empty, meaning no variables are captured. The(int a, int b)part defines the parameters, while{ return a + b; }is the function body that adds the two numbers. For example, we could write:int sum = std::accumulate(ALL(vec), 0, [](int a, int b) { return a + b; });This lambda sums all elements in
v. Nevertheless, the C++ provides standard functions for common operations instd::accumulate.int sum = std::accumulate(All(vec), 0, std::plus<>());
std::plus<>adds two numbers. It’s the default forstd::accumulate.int product = std::accumulate(ALL(vec), 1, std::multiplies<>());
std::multiplies<>multiplies two numbers.Using lambda functions, or not, you can create your own functions.
int max_element = std::accumulate(ALL(vec), v[0], [](int a, int b) { return std::max(a, b); });This lambda function finds the largest element in
v. In this case,std::accumulateapplies the function repeatedly. It starts with an initial value. For each element:
- It takes the previous result.
- It takes the current element.
- It applies the function to both values.
- The result is used in the next iteration.
This process continues until the sequence ends. Let’s see how
std::accumulatesums the squares of numbers:std::vector<int> vec = {1, 2, 3, 4}; int sum_of_squares = std::accumulate(ALL(vec), 0, [](int acc, int x) { return acc + x * x; });The process goes like this:
- Start: $acc = 0$
- For $1$: $acc = 0 + 1 * 1 = 1$
- For $2$: $acc = 1 + 2 * 2 = 5$
- For $3$: $acc = 5 + 3 * 3 = 14$
- For $4$: $acc = 14 + 4 * 4 = 30$
The final result is $30$.
1.2.2.3. Using Lambda Functions
Let’s can back to Lambdas.
Starting with C++11, C++ introduced lambda functions. Lambdas are anonymous functions that can be defined exactly where they are needed. If your code needs a simple function used only once, you should consider using lambdas. Let’s start with a simple example, Code 1.2.B, written without competitive programming tricks.
#include <iostream> // Includes the input/output stream library for console operations
#include <vector> // Includes the vector library for using dynamic arrays
#include <algorithm> // Includes the algorithm library for functions like sort
// Traditional function to sort in descending order
bool compare(int a, int b) {
return a > b; // Returns true if 'a' is greater than 'b', ensuring descending order
}
int main() {
std::vector<int> numbers = {1, 3, 2, 5, 4}; // Initializes a vector of integers
// Uses the compare function to sort the vector in descending order
std::sort(numbers.begin(), numbers.end(), compare);
// Prints the sorted vector
for (int num : numbers) {
std::cout << num << " "; // Prints each number followed by a space
}
std::cout << "\n"; // Prints a newline at the end
return 0; // Returns 0, indicating successful execution
}
Code 1.2.B: Code example to sort a number vector and print it. {: class=”legend”}
The Code 1.2.B sorts a vector of integers in descending order using a traditional comparison function. It begins by including the necessary libraries: <iostream> for input and output, <vector> for dynamic arrays, and <algorithm> for sorting operations. The compare function is defined to take two integers, returning true if the first integer is greater than the second, setting the sorting order to descending.
In the main function, a vector named numbers is initialized with the integers {1, 3, 2, 5, 4}. The std::sort function is called on this vector, using the compare function to sort the elements from highest to lowest. After sorting, a for loop iterates through the vector, printing each number followed by a space. The program ends with a newline to cleanly finish the output. This code is a simple and direct example of using a custom function to sort data in C++. Now, let’s see the same code using lambda functions and other competitive programming tricks, Code 1.2.C:
#include <iostream> // Includes the input/output stream library for console operations
#include <vector> // Includes the vector library for using dynamic arrays
#include <algorithm> // Includes the algorithm library for functions like sort
#define ALL(vec) vec.begin(), vec.end() // Macro to simplify passing the entire range of a vector
using VI = std::vector<int>; // Alias for vector<int> to simplify code and improve readability
int main() {
VI num = {1, 3, 2, 5, 4}; // Initializes a vector of integers using the alias VI
// Sorts the vector in descending order using a lambda function
std::sort(ALL(num), [](int a, int b) { return a > b; });
// Prints the sorted vector
for (int n : num) {
std::cout << n << " "; // Prints each number followed by a space
}
std::cout << "\n"; // Prints a newline at the end
return 0; // Returns 0, indicating successful execution
}
Code 1.2.C: Sort and print vector using lambda functions.
To see the typing time gain, just compare the normal definition of the compare function followed by its usage with the use of the lambda function.
The Code 1.2.C sorts a vector of integers in descending order using a lambda function, a modern and concise way to define operations directly in the place where they are needed. It starts by including the standard libraries for input/output, dynamic arrays, and algorithms. The macro ALL(vec) is defined to simplify the use of vec.begin(), vec.end(), making the code cleaner and shorter.
An alias VI is used for std::vector<int>, reducing the verbosity when declaring vectors. Inside the main function, a vector named num is initialized with the integers {1, 3, 2, 5, 4}. The std::sort function is called to sort the vector, using a lambda function [](int a, int b) { return a > b; } that sorts the elements in descending order.
The lambda is defined and used inline, removing the need to declare a separate function like compare. After sorting, a for loop prints each number followed by a space, ending with a newline. This approach saves time and keeps the code concise, highlighting the effectiveness of lambda functions in simplifying tasks that would otherwise require traditional function definitions.
Lambda functions in C++, introduced in C++11, are anonymous and defined where they are needed. They shine in short, temporary tasks like inline calculations or callbacks. Unlike regular functions, lambdas can capture variables from their surrounding scope. With C++20, lambdas became even more powerful and flexible, extending their capabilities beyond simple operations.
The general syntax for a lambda function in C++ is as follows:
[capture](parameters) -> return_type { // function body};Where:
Capture: Specifies which variables from the surrounding scope can be used inside the lambda. Variables can be captured by value[=]or by reference[&]. You can also specify individual variables, such as[x]or[&x], to capture them by value or reference, respectively.Parameters: The input parameters for the lambda function, similar to function arguments.Return Type: Optional in most cases, as C++ can infer the return type automatically. However, if the return type is ambiguous or complex, it can be specified explicitly using-> return_type.Body: The actual code to be executed when the lambda is called.C++20 brought new powers to lambdas. Now, they can be used in immediate functions, which are functions marked with
constevalthat must be evaluated entirely at compile-time. This makes the code faster by catching errors early and optimizing performance. Lambdas can also be default-constructed without capturing anything, meaning they don’t rely on external variables. Additionally, they support template parameters, allowing lambdas to work with different data types, making them more flexible and generic. Let’s see some examples.Example 1: Basic Lambda Function: A simple example of a lambda function that sums two numbers:
auto sum = [](int a, int b) -> int {return a + b;}; std::cout << sum(5, 3); // Outputs: 8Example 2: Lambda with Capture: In this example, a variable from the surrounding scope is captured by value:
int x = 10; // Initializes an integer variable x with the value 10 // Defines a lambda function that captures x by value (creates a copy of x) auto multiply = [x](int a) {return x * a;}; // Multiplies the captured value of x by the argument a std::cout << multiply(5); // Calls the lambda with 5; Outputs: 50Here, the lambda captures
xby value and uses it in its body. This meansxis copied when the lambda is created. The lambda holds its own version ofx, separate from the original. Changes toxoutside the lambda won’t affect the copy inside. It’s like taking a snapshot ofxat that moment. The lambda works with this snapshot, keeping the original safe and unchanged. But this copy comes at a cost—extra time and memory are needed. For simple types like integers, it’s minor, but for larger objects, the overhead can add up.Example 3: Lambda with Capture by Reference: In this case, the variable
yis captured by reference, allowing the lambda to modify it:int y = 20; // Initializes an integer variable y with the value 20 // Defines a lambda function that captures y by reference (no copy is made) auto increment = [&y]() { y++; // Increments y directly }; increment(); // Calls the lambda, which increments y std::cout << y; // Outputs: 21In this fragment, there’s no extra memory or time cost. The lambda captures
yby reference, meaning it uses the original variable directly. No copy is made, so there’s no overhead. Whenincrement()is called, it changesyright where it lives. The lambda works with the realy, not a snapshot, so any change happens instantly and without extra resources. This approach keeps the code fast and efficient, avoiding the pitfalls of capturing by value. The result is immediate and uses only what’s needed. In competitive or high-performance programming, we capture by reference. It’s faster and uses less memory.Example 4: Generic Lambda Function with C++20: With C++20, lambdas can now use template parameters, making them more generic:
// Defines a generic lambda function using a template parameter <typename T> // The lambda takes two parameters of the same type T and returns their sum auto generic_lambda = []<typename T>(T a, T b) { return a + b; }; std::cout << generic_lambda(5, 3); // Calls the lambda with integers, Outputs: 8 std::cout << generic_lambda(2.5, 1.5); // Calls the lambda with doubles, Outputs: 4.0This code defines a generic lambda using a template parameter, a feature from C++20. The lambda accepts two inputs of the same type
Tand returns their sum. It’s flexible—first, it adds integers, then it adds doubles. The power of this lambda is in its simplicity and versatility. It’s short, clear, and works with any type as long as the operation makes sense. C++20 lets you keep your code clean and adaptable, making lambdas more powerful than ever. And it doesn’t stop there.In C++20, lambdas that don’t capture variables can be default-constructed. This means you can create, assign, and save them for later use without calling them immediately. This feature is useful for storing lambdas as placeholders for default behavior, making them handy for deferred execution. As you can see in Code 1.2.D
#include <iostream> #include <vector> #include <algorithm> #define ALL(vec) vec.begin(), vec.end() // Macro to simplify passing the entire range of a vector using VI = std::vector<int>; // Alias for vector<int> to simplify code and improve readability // Define a default-constructed lambda that prints a message auto print_message = []() {std::cout << "Default behavior: Printing message." << "\n";}; int main() { // Store the default-constructed lambda and call it later print_message(); // Define a vector and use the lambda as a fallback action VI num = {1, 2, 3, 4, 5}; // If vector is not empty, do something; else, call the default lambda if (!num.empty()) { std::for_each(ALL(num), [](int n) {std::cout << n * 2 << " ";}); // Prints double of each number } else { print_message(); // Calls the default lambda if no numbers to process } return 0; }Code 1.2.D: Using lambdas default-constructed.
This feature lets you set up lambdas for later use (deferred execution). In the Code 1.2.D, the lambda
print_messageis default-constructed. It captures nothing and waits until it’s needed. The main function shows this in action. If the vector has numbers, it doubles them. If not, it calls the default lambda and prints a message. C++20 makes lambdas simple and ready for action, whenever you need them.We also have the immediate lambdas: C++20 brings in
consteval, a keyword that forces functions to run at compile-time. With lambdas, this means the code is executed during compilation, and the result is set before the program starts. When a lambda is used in aconstevalfunction, it must run at compile-time, making your code faster and results predictable. In programming competitions,constevallambdas are rarely useful. Contests focus on runtime performance, not compile-time tricks. Compile-time evaluation doesn’t give you an edge when speed at runtime is what counts. Most problems don’t benefit from execution before the program runs; the goal is to be fast during execution.Nevertheless,
Constevalensures the function runs only at compile-time. If you try to use aconstevalfunction where it can’t run at compile-time, you’ll get a compile-time error. It’s strict: no runtime allowed.consteval auto square(int x) { return [] (int y) { return y * y; }(x); } int value = square(5); // Computed at compile-timeIn this example, the lambda inside the
squarefunction is evaluated at compile-time, producing the result before the program starts execution. Programming contests focus on runtime behavior and dynamic inputs, makingconstevalmostly useless. In contests, you deal with inputs after the program starts running, so compile-time operations don’t help. The challenge is to be fast when the program is live, not before it runs.Finally, we have template lambdas: C++20 lets lambdas take template parameters, making them generic. They can handle different data types without needing overloads or separate template functions. The template parameter is declared right in the lambda’s definition, allowing one lambda to adapt to any type.
Example:
auto generic_lambda = []<typename T>(T a, T b) { return a + b; }; std::cout << generic_lambda(5, 3); // Outputs: 8 std::cout << generic_lambda(2.5, 1.5); // Outputs: 4.0Template lambdas are a powerful tool in some competitive programming. They let you write one lambda that works with different data types, saving you time and code. Instead of writing multiple functions for integers, doubles, or custom types, you use a single template lambda. It adapts on the fly, making your code clean and versatile. In contests, where every second counts, this can speed up coding and reduce bugs. You get generic, reusable code without the hassle of writing overloads or separate templates.
Lambdas are great for quick, one-time tasks. But too many, especially complex ones, can make code harder to read and maintain. In competitive programming, speed often trumps clarity, so this might not seem like a big deal. Still, keeping code readable helps, especially when debugging tough algorithms. Use lambdas wisely.
Complete Series
References
-
Silberschatz, A., Galvin, P. B., & Gagne, G. (2013). Operating system concepts essentials (2nd ed.). John Wiley & Sons. ↩
