O Eletromagnetismo é a lei, o ordenamento que embala o universo. Como uma divindade antiga que rege a existência e os movimentos de tudo que existe. Duas forças, elétrica e magnética, em uma dança interminável, moldam de um grão de poeira a um oceano de estrelas, até o mesmo dispositivo que você usa para decifrar essas palavras deve sua existência e funcionamento ao Eletromagnetismo.

Imagem de Asimina Nteliou de Pixabay

“Nesta longa vida eu aprendi que toda a nossa ciência se comparada com a realidade é primitiva e infantil. Ainda assim, é a coisa mais preciosa que temos.” Albert Einstein

1. Álgebra Vetorial
   1. Vetores, os compassos de tudo que há e haverá
      1. Exercício 1
   2. Vetores Unitários
      1. Exercício 2
      2. Exercício 3
   3. Multiplicação por Escalar
   4. Vetor Oposto
   5. Adição e Subtração de Vetores
   6. Exercício 4
      1. Exercício 5
      2. Exercício 6
      3. Exercício 7
      4. Exercício 8
   7. Vetores Posição e Distância
      1. Exercício 9
      2. Exercício 10
   8. Produto Escalar
      1. Exercício 11
      2. Exercício 12
      3. Exercício 13
   9. Produto Vetorial
      1. Exercício 14
   10. Produto Triplo Escalar
2. PRECISA REESCREVER PARA INCLUIR O CONCEITO DA REGRA DA MÃO DIREITA
3. Usando a Álgebra Vetorial no Eletromagnetismo
   1. Lei de Coulomb
4. Cálculo Vetorial
   1. Campos Vetoriais
   2. Gradiente
      1. Significado do Gradiente
      2. Propriedades do Gradiente
   3. Divergência
      1. Fluxo e a Lei de Gauss
      2. Teorema da Divergência
      3. Propriedades da Divergência
   4. Rotacional

Estudaremos linhas de força invisíveis que se entrelaçam, tangenciam e interferem umas nas outras, formando o tecido do Cosmos e o fluxo da vida, tão real quanto a terra sob os pés ou o ar que respiramos, e como este último, completamente invisíveis.

O estudo do Eletromagnetismo será uma batalha própria, individual, dura. É a esperança lançar luz sobre o desconhecido, descobrir as regras que governam a vida e o universo, e então aproveitar essas regras para criar, para progredir, para sobreviver. Não é para os fracos de coração, nem para aqueles que buscam respostas fáceis. É para aqueles que não temem o desconhecido, para os que se levantam diante do abismo do desconhecido e dizem: eu entenderei.

O estudo do Eletromagnetismo é um desafio, uma luta, um chamado. E, como em qualquer luta, haverão perdas, dores, mas também alegrias, triunfos e, no final de tudo, um compreensão diferente de tudo que está ao seu redor. Esta é uma jornada que começou a milhares de anos, e deverá continuar por outro tanto. Prepare-se sua forma de ver o universo vai mudar.

Quando o século XIX caminhava para seu final, James Clerk Maxwell, orquestrou as danças dos campos elétrico e do magnético em uma sinfonia de equações. Desenhando na tela do universo, Maxwell delineou a interação dessas forças com o espaço e a matéria. Sua obra, extraordinária em todos os aspectos, destaca-se pela simplicidade refinada e pela beleza lírica. Um balé de números, símbolos e equações que desliza pela folha, fluido e elegante como um rio.

Mas essa beleza, essa simplicidade, não é acessível a todos. Ela é um jardim murado, reservado àqueles que conquistaram o direito de entrar através de estudo e compreensão. Sem o conhecimento apropriado, seja da física que fundamenta o universo ou da matemática que o descreve, as equações de Maxwell são como flores de pedra: frias, inalteráveis, sem vida. Com esse entendimento, no entanto, elas florescem em cores e formas maravilhosas, vivas e palpitantes com significado.

Aqui embarcamos na nossa jornada! Uma exploração desse jardim de pedras e sombras, na busca da beleza oculta na rispidez fria do desconhecimento. Neste livro nosso foco estará no entendimento da matemática que define, e explica, as equações que estruturam o entendimento do universo. Nosso interesse começará no abstrato, no puro, na dança dos números e símbolos que compõem estas equações e terminará, paulatinamente na análise dos fenômenos que a matemática explica. Há uma vã esperança que esta estratégia crie as estruturas cognitivas que a amável leitora precisará para entender estes fenômenos e ir além desta modesta introdução.

Considere este texto como se estivesse liberando a nau do seu conhecimento das toas do porto da ignorância. Este é o início da sua jornada em um mar de dúvidas. Dúvidas intrigantes, excitantes e provocativas. Quase um enigma. Gosta de enigmas? Precisa vencer estes desafios? Tem a satisfação de resolvê-los? Se sim, embarque nesta viagem em busca do conhecimento mais estruturante do Universo. Talvez você chegue lá, talvez não.

Lágrimas de decepção não a encontrarão em cada porto. Isso eu posso garantir. Da mesma forma que posso antever todo o cansaço, frustração e a dor resultantes do esforço do aprendizado. Aprender, nunca é fácil. Mesmo que nossa nau não chegue ao destino desejado. Cada porto de entendimento lhe trará o presente do conhecimento no final você será uma pessoa diferente. São mares revoltos, não será fácil. Mas estaremos juntos. Eu estarei no leme, o tempo todo, tentando encontrar bons ventos e evitar mares revoltos. Como diria o poeta:

“…Tudo vale a pena Se a alma não é pequena…”. Fernando Pessoa.

Álgebra Vetorial

Área da matemática envolvida com o espaço, vetores e seu baile atemporal, ritmado por regras intrínsecas e características do espaço. Vetores e Matrizes, soldados organizados em linhas e colunas, cada um contando histórias de variáveis e transformações. Divergências, gradientes e rotacionais, gestos majestosos na dança do cálculo vetorial. Tudo tão complexo quanto a vida, tão real quanto a morte, tão honesto quanto o mar, profundo, impiedoso e direto.

O mar bravo só respeita rei. Arnaud Rodrigues / Chico Anísio

O espaço será definido por vetores, cheio de mistério e beleza. A Análise vetorial será a bússola do navegante, guiando-o através do vasto oceano do desconhecido. A cada dia, a cada cálculo, desvendaremos um pouco mais desse infinito, mapearemos um pouco mais desse oceano de números, direções, sentidos e valores, entendemos um pouco mais de como o Universo dança ao som da álgebra linear e da análise vetorial.

Existe uma pequena diferença entre a álgebra vetorial e a álgebra linear. Esta última tem uma estrutura rígida e formal que, sempre que possível, eu irei ignorar na esperança de tornar mais simples a compreensão. Por isso escolhi o campo da álgebra vetorial. O mesmo campo de estudo, com menos formalidade e mais aplicação. Este é um escambo, estou trocando a beleza da rigidez matemática pela simplicidade nas operações. O vetor é o elemento primitivo da álgebra vetorial, e por ele começaremos.

Vetores, os compassos de tudo que há e haverá

Vetores, feixes silenciosos de informação, conduzem o entendimento além do simples tamanho. São como bússolas com uma medida, apontando com determinação e direção para desvendar os segredos das grandezas que precisam mais do que só a magnitude. Vetores, abstrações matemáticas que usamos para entender as gradezas que precisam de direção e sentido além da pura magnitude. Parecem ser o resultado da mente brilhante de Simon Stevin que, estudando mecânica teve a estudando hidrostática, propôs uma regra empírica para resolver o problema de duas forças, ou mais forças, aplicadas no mesmo ponto por meio de uma regra que hoje conhecemos como a Regra do Paralelogramo publicada em De Beghinselen der Weeghconst (1586; em tradução livre: Estática e Hidrostática). Usamos vetores para superar as limitações das grandezas escalares, incluindo em uma mesma representação amplitude, direção e sentido.

As grandezas escalares, aquelas que podem ser medidas como medimos a massa de um peixe, o tempo que demora para o sol se pôr ou a velocidade de um veleiro cortando a paisagem em linha, quisera eu, reta. Cada grandeza escalar é um número único, uma quantidade, uma magnitude. Um fato em si mesmo carregando todo o conhecimento necessário para seu entendimento ¹.

São as contadoras de histórias silenciosas do mundo, falando de tamanho, de quantidade, de intensidade. E, como um bom whisky, sua força reside na simplicidade. Ainda assim, as grandezas escalares oferecem uma medida da verdade.

As grandezas vetoriais, por outro lado são complexas, diversas e intrigantes. Vetores são as abstrações que para entender estas grandezas, guerreiras da direção e do sentido. Navegam o mar da matemática com uma clareza de propósito que vai além da mera magnitude. Elas possuem uma seta, uma bússola, que indica para onde se mover. Sobrepujam o valor em si com uma direção, um sentido, uma indicação, uma seta. E fazemos assim, usamos setas em respeito as ideias de Gaspar Wessel que em seu trabalho On the Analytical Representation of Direction de 1778 sugeriu o uso de linhas orientadas para indicar o ponto onde duas linhas se cruzam o mesmo conceito que usamos em somas de vetores. A seta, nossa amiga contemporânea, surge no trabalho de Jean-Victor Poncelet trabalhando em problemas de engenharia e usando as regras definidas por Stevin e o conceito de direção de Wessel, resolver usar uma seta para indicar uma força. E assim, as mãos e a mente de um engenheiro deram a luz aos vetores.

A seta, uma extensão de ser do próprio vetor, representa sua sua orientação. Aponta o caminho para a verdade, mostrando não apenas o quanto, mas também o onde. Seu indica sua magnitude, o quanto, sua essência. Assim vetores escondem intensidade, direção e sentido em uma única entidade, fugaz e intrigante.

As grandezas vetoriais são como o vento, cuja direção e força você sente, mas cuja essência não se pode segurar. Elas são como o rio, cujo fluxo e direção moldam a paisagem. São essenciais para entender o mundo em movimento, o mundo de forças, velocidades e acelerações. Elas dançam nas equações do eletromagnetismo, desenham os padrões da física e guiam os marinheiros na imensidão do desconhecido. No mar da compreensão, grandezas vetoriais são a bússola e o vento, dando não apenas escala, mas também orientação e sentido à nossa busca pelo conhecimento. Como é belo o idioma de Machado de Assis, mas, de tempos em tempos, temos que recorrer as imagens. Toda esta poesia pode ser resumida na geometria de uma seta com origem e destino em um espaço multidimensional contendo informações de direção, sentido e intensidade.

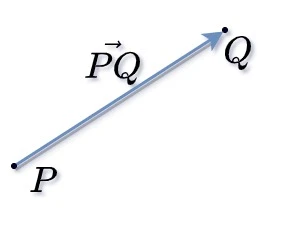
Nesta jornada, não seremos limitados pela frieza da geometria. Buscamos a grandeza da álgebra. Na álgebra vetores são representados por operações de soma entre outros vetores.

Tentarei, juro que tentarei, limitar o uso da geometria ao mínimo necessário para o entendimento dos conceitos relacionados a aplicação das forças, e campos, que usaremos para entender o universo do eletromagnetismo.

Na física moderna, quântica principalmente, usamos os vetores como definido por Dirac (1902-1984), que chamamos de Vetores Ket, ou simplesmente ket. Não aqui, pelo menos não por enquanto. Aqui utilizaremos a representação vetorial como definida por Willard Gibbs (1839–1903) no final do Século XIX. Adequada ao estudo clássico do Eletromagnetismo. O estudo das forças que tecem campos vetoriais que abraçam a própria estrutura do Universo. Invisíveis porém implacáveis.

Entender esses campos é uma forma de começar a entender o universo. É ler a história que está sendo escrita nas linhas invisíveis de força. É mergulhar no mar profundo do desconhecido, e emergir com um conhecimento novo e precioso. É se tornar um tradutor da linguagem cósmica, um leitor das marcas deixadas pelas forças em seus campos. É, em resumo, a essência da ciência. E é essa ciência, esse estudo dos campos e das forças que neles atuam, que iremos explorar. Para nós, sedentos de curiosidade, campos serão funções capazes de especificar valores em qualquer ponto de uma dada região do espaço ¹.

Para lançar as pedras fundamentais do nosso conhecimento representaremos os vetores por meio de letras latinas maiúsculas $\, \vec{A}, \vec{B}, \vec{C}, …$ marcadas com uma pequena seta. Estes vetores serão os elementos construtivos de um espaço vetorial $\mathbf{V}$. Como a leitora pode ver espaços vetoriais também serão representados por letras latinas maiúsculas, desta feita em negrito.

Neste texto introdutório, mapa de nossa jornada, os espaços vetoriais serão sempre representados em três dimensões. O espaço que procuramos é o nosso, o espaço onde vivemos, a forma como percebemos mares, montanhas, planícies, o céu, nosso universo.

Não é qualquer espaço, é um espaço específico, limitado à realidade e limitante das operações que podemos fazer com os elementos deste espaço. Assim, nosso estudo se fará a partir de um espaço vetorial específico. Um espaço vetorial $\mathbf{V}$ que satisfaça às seguintes condições:

1. o espaço vetorial $\mathbf{V}$ seja fechado em relação a adição. Isso quer dizer que para cada par de vetores $\vec{A}$ e $\vec{B}$ pertencentes a $\mathbf{V}$ existe um, e somente um, vetor $\vec{C}$ que representa a soma de $\vec{A}$ e $\vec{B}$ e que também pertence ao espaço vetorial $\mathbf{V}$, dizemos que:

   \[\exists \, \vec{A} \in \mathbf{V} \wedge \exists \vec{B} \in \mathbf{V} \therefore \exists (\, \vec{a}+\vec{B}=\vec{C}) \in \mathbf{V}\]

2. a adição seja associativa:

   \[(\, \vec{A}+\vec{B})+\vec{C} = \, \vec{a}+(\vec{B}+\vec{C})\]

3. existe um vetor zero: a adição deste vetor zero a qualquer vetor $\, \vec{A}$ resulta no próprio vetor $\, \vec{A}$, inalterado, imutável. De tal forma que:

   \[\forall \, \vec{A} \in \mathbf{V} \space \space \exists \wedge \vec{0} \in \space \mathbf{V} \space \therefore \space \vec{0}+\, \vec{A}=\, \vec{A}\]

4. existe um vetor negativo $-\, \vec{A}$ de forma que a soma de um vetor com seu vetor negativo resulta no vetor zero. Tal que:

   \[\exists -\, \vec{A} \in \mathbf{V} \space \space \vert \space \space -\, \vec{A}+\, \vec{A}=\vec{0}\]

5. o espaço vetorial $\mathbf{V}$ seja fechado em relação a multiplicação por um escalar, um valor sem direção ou sentido, de tal forma que para todo e qualquer elemento $c$ do conjunto dos números complexos $\mathbb{C}$ multiplicado por um vetor $\, \vec{a}$ do espaço vetorial $\mathbf{V}$ existe um, e somente um vetor $c\, \vec{a}$ que também pertence ao espaço vetorial $\mathbf{V}$. Tal que:

   \[\exists \space c \in \mathbb{C} \space \space \wedge \space \space \exists \space \, \vec{A} \in \mathbf{V} \space \space \therefore \space \space \exists \space c\, \vec{A} \in \mathbf{V}\]

6. Existe um escalar neutro $1$: tal que a multiplicação de qualquer vetor $\vec{A}$ por $1$ resulta em $\, \vec{A}$. Ou seja:

   \[\exists \space 1 \in \mathbb{R} \space \space \wedge \space \space \exists \space \, \vec{A} \in \mathbf{V} \space \space \vert \space \space 1\, \vec{A} = \, \vec{A}\]

É preciso manter a atenção voltada para a hierarquia que rege o mundo dos conjuntos. O conjunto dos números reais $\mathbb{R}$ é um subconjunto do conjunto dos números imaginários $\mathbb{C}={a+bi \space \space a.b \in \mathbb{R}}$. Esta relação de pertencimento determina que o conjunto $\mathbb{R}$, o conjunto dos números reais, se visto de forma mais abrangente, representa de forma concisa, todos os números imaginários cuja parte imaginária é igual a zero. Se usarmos a linguagem da matemática dizemos que:

\[\mathbb{R}=\{a+bi \space \space \vert \space \space a.b \in \mathbb{R} \wedge b=0\}\]

A representação algébrica dos vetores definida por Willard Gibbs (1839–1903), que usaremos neste documento, indica que um vetor em um espaço vetorial $\mathbf{V}$ qualquer é, pura e simplesmente, o resultado de operações realizadas entre os vetores que definem os componentes deste espaço vetorial.

Já sabemos que nosso espaço $\mathbf{V}$ será formado em três dimensões então precisamos escolher um conjunto de coordenadas, que definam os pontos deste espaço e usar estes pontos para determinar os componentes vetoriais que usaremos para especificar todos os vetores do espaço $\mathbf{V}$.

Maxwell, seguindo os passos de Newton, também se apoiou nos ombros de gigantes. E eis que em nossa jornada nos defrontamos com um destes gigantes. Em meados do Século XVII, René Descartes criou um sistema de coordenadas definindo o espaço que conhecemos. Tão preciso, simples e eficiente que prevaleceu contra o tempo e até hoje leva o nome latino do seu criador: Sistema de Coordenadas Cartesianas.

Vetores, são setas que representam forças, uma metáfora, uma abstração matemática que permite o entendimento do universo por meio da análise das forças que o compõem, definem e movimentam. Definimos um vetor simplesmente observando seu ponto de origem e destino, marcando estes pontos no espaço e traçando um seta ligando estes dois pontos. E isso deixaremos no domínio da geometria sempre que pudermos. Na álgebra do mundo real, este que estamos estudando, vetores serão definidos pela subtração. O vetor será definido pelas coordenadas do ponto de destino é o ponto de origem. Fica claro quando usamos o Sistema de Coordenadas Cartesianas.

Exercício 1

Em uma tarde quente em um bar à beira-mar, um velho pescador conversava com um jovem aprendiz sobre os vetores. “Eles são como o vento, têm direção, sentido e intensidade”, disse o pescador. “Imagine dois pontos no mar, e queremos saber a direção e força do vento entre eles”. Ele desenhou no chão com um pedaço de carvão os pontos: A(1,2,3) e B(-1,-2,3). “Agora”, ele perguntou, “como determinamos o vetor entre esses dois pontos?”

No Sistema de Coordenadas Cartesianas, limitamos o espaço com três eixos, perpendiculares e ortogonais e pelos valores das coordenadas $(x,y.z)$ colocadas sobre estes eixos. Do ponto de vista da Álgebra Vetorial, para cada um destes eixos teremos um vetor de comprimento unitário. São estes vetores, que chamamos de vetores unitários e identificamos por $(\, \vec{a}_x, \, \vec{a}_y, \, \vec{a}_z)$ respectivamente, Chamamos estes vetores de unitários porque têm magnitude $1$ e estão orientados segundo os eixos cartesianos $(x,y,z)$.

Lembrando: a magnitude de um vetor é seu comprimento. Vetores unitários tem comprimento $1$.

O encanto da matemática se apresenta quando dizemos que todos os vetores do espaço vetorial $\mathbf{V}$ podem ser representados por somas dos vetores unitários $(\, \vec{a}_x, \, \vec{a}_y, \, \vec{a}_z)$ desde que estes vetores sejam multiplicados independentemente por fatores escalares. Isto implica, ainda que não fique claro agora, que qualquer vetor no espaço será o produto de um vetor unitário por um escalar. Para que fique claro temos que entender os vetores unitários.

Vetores Unitários

Um vetor $\vec{B}$ qualquer tem magnitude, direção e sentido. A magnitude, também chamada de intensidade, módulo, ou comprimento, será representada por $ \vert \vec{B} \vert $. Definiremos um vetor unitário $\, \vec{a}$ na direção $\vec{B}$ por $\, \vec{a}_B$ de tal forma que:

\[\, \vec{a}_B=\frac{\vec{B}}{|\vec{B}|}\]

Um vetor unitário $\, \vec{a}_B$ é um vetor que tem a mesma direção e sentido de $\vec{B}$ com magnitude $1$ logo o módulo, ou magnitude, ou ainda comprimento de $\, \vec{a}_b$ será representado por:

\[\vert \, \vec{a}_B \vert =1\]

Agora que conhecemos os vetores unitários podemos entender as regras que sustentam a Álgebra Vetorial e fazem com que todos os conceitos geométricos que fundamentaram a existência de vetores possam ser representados algebricamente, sem linhas nem ângulos, em um espaço, desde que este espaço esteja algebricamente definido em um sistema de coordenadas. Aqui, usaremos sistemas de coordenadas tridimensionais.

Em um sistema de coordenadas tridimensionais ortogonais podemos expressar qualquer vetor na forma da soma dos seus componentes unitários ortogonais. Qualquer vetor, independente da sua direção, sentido, ou magnitude pode ser representado pela soma dos os vetores unitários que representam as direções, eixos e coordenadas, do sistema de coordenadas escolhido. A cada fator desta soma daremos o nome de componente vetorial, ou simplesmente componente. Existirá um componente para cada dimensão do sistema de coordenadas e estes componentes são específicos do sistema de coordenadas que escolhermos para representar o espaço que chamaremos $\mathbf{V}$.

Como somos marinheiros de primeira viagem, navegamos de dia, em mares conhecidos mantendo a terra a vista. Neste caso, começaremos com o Sistema de Coordenadas Cartesianas. Um sistema de coordenadas conhecido, seguro e fácil de representar. Não será difícil visualizar um espaço vetorial definido neste sistema já que é o espaço em que vivemos. A sala de sua casa tem uma largura $x$, um comprimento $y$ e uma altura $z$. No Sistema de Coordenadas Cartesianas a representação de um vetor $\vec{B}$ qualquer, segundo seus componentes unitários e ortogonais será dada por:

\[\vec{B}=b_x\, \vec{a}_x+b_y\, \vec{a}_y+b_z\, \vec{a}_z\]

Nesta representação, $b_x$, $b_y$, $b_z$ representam os fatores escalares que devemos usar para multiplicar os vetores unitários $\, \vec{a}_x$, $\, \vec{a}_y$, $\, \vec{a}_z$ de forma que a soma destes vetores represente o vetor $B$ no espaço $\Bbb{R}^3$.

Aqui chamaremos $b_x$, $b_y$, $b_z$ de componentes vetoriais nas direções $x$, $y$, $z$, ou de projeções de $\vec{B}$ nos eixos $x$, $y$, $z$. A prova da equivalência entre os componentes e as projeções sobre os eixos pertence ao domínio da geometria que ficou no porto na hora em que começamos esta viagem.

A simplicidade do Sistema de Coordenadas Cartesianas é também a sua maldição. Estudando Eletromagnetismo enfrentaremos muitos problemas nos quais o uso deste sistema tornará a matemática desnecessariamente torturante. Neste caso podemos recorrer a qualquer outro sistema de coordenadas. Com a única condição de termos três dimensões ortogonais entre si. Por exemplo, poderíamos definir nosso vetor $\vec{B}$ como:

\[\vec{B}=b_x\, \vec{a}_x+b_y\, \vec{a}_y+b_z\, \vec{a}_z\] \[\vec{B}=b_r\, \vec{a}_r+b_\phi \, \vec{a}_\phi+b_z\, \vec{a}_z\] \[\vec{B}=b_r\, \vec{a}_r+b_\phi \, \vec{a}_\phi+b_\theta \, \vec{a}_\theta\]

Respectivamente para os Sistemas de Coordenadas Cartesianas, Cilíndricas e Esféricas.

Sistemas de coordenadas diferentes para o mesmo espaço são como diferentes mapas náuticos para o mesmo oceano. Em cada mapa, o norte ainda é o norte e uma constelação ainda a guiará ao porto. O vetor $\vec{B}$ mantém sua magnitude, direção e sentido, não importa qual carta náutica você desenrole sobre a mesa. E quando for necessário transitar entre esses sistemas, faremos isso com a precisão de um pescador experiente mergulhando nas profundezas azuis para recuperar um arpão precioso. Não tenha dúvidas, o essencial permanecerá constante; apenas o meio mudará. E, quando for necessário, estudaremos estes sistemas para entender como mapas diferentes mostram o mesmo oceano.

A matemática, tal qual o mar, guarda suas próprias surpresas. Às vezes, depois de definir o sistema de coordenadas como um velho marinheiro escolhe sua rota, os vetores se desnudam até suas essências mais simples, suas componentes vetoriais, deixando para trás os vetores unitários como um navio abandona seu lastro. No Sistema de Coordenadas Cartesianas, o vetor $\vec{B} = 3\, \vec{a}_x + \, \vec{a}_y - \, \vec{a}_z$ se transforma, e pode ser representado apenas por suas coordenadas $\vec{B} = (3, 1, -1)$, como um navio que içou suas velas, pronto para a jornada, livre do peso desnecessário. A substância permanece, enquanto a forma se adapta ao desafio do momento. Durante a árdua tarefa de resolver seus próprios problemas você terá que escolher como representará seus vetores. Eu, volúvel que sou, hora escreverei $\vec{B} = 3\, \vec{a}_x + \, \vec{a}_y - \, \vec{a}_z$ ora escreverei $\vec{B} = (3, 1, -1)$. Caberá a paciente leitora a tarefa da interpretação, extrato da atenção e do aprendizado.

Se tivermos um vetor $\vec{B} = b_x\, \vec{a}_x + b_y\, \vec{a}_y + b_z\, \vec{a}_z$ sua magnitude será dada por:

\[\vert \vec{B} \vert =\sqrt{ {b_x}^2 + {b_y}^2 + {b_z}^2}\]

A princípio fugirá a percepção da amável leitora, mas é fato que desta forma poderemos encontrar o vetor unitário ${\, \vec{a}_B}$, que leremos vetor unitário a na direção do vetor $\vec{B}$ por:

\[\, \vec{a}_B=\frac{ \vec{B} }{ \vert \vec{B} \vert }= \frac{b_x\, \vec{a}_x+b_y\, \vec{a}_y+b_z\, \vec{a}_z}{ \sqrt{b_x^2+b_y^2+b_z^2} }\]

Equação que deve ser lida como: o vetor unitário de um dado vetor será o próprio vetor dividido pela sua magnitude. Talvez toda essa rigidez da matemática desvaneça diante dos seus olhos, lindos e cansados, se recorrermos a um exemplo.

Exemplo 1:
Calcule o vetor unitário $\, \vec{a}_A$ do vetor $\, \vec{a}=\, \vec{a}_x-3\, \vec{a}_y+2\, \vec{a}_z$.

Solução: partindo da definição de vetor unitário. \[\, \vec{a}_A=\frac{\, \vec{a}_x\, \vec{a}_x+\, \vec{a}_y\, \vec{a}_y+\, \vec{a}_z\, \vec{a}_z}{\sqrt{\, \vec{a}_x^2+\, \vec{a}_y^2+\, \vec{a}_z^2} }\] Substituindo os valores, dados no enunciado: \[\, \vec{a}_A=\frac{\, \vec{a}_x-3\, \vec{a}_y+2\, \vec{a}_z}{\sqrt{1^2+(-3)^2+2^2} }=\frac{\, \vec{a}_x-3\, \vec{a}_y+2\, \vec{a}_z}{3,7416}\] \[\, \vec{a}_A=0,2672\, \vec{a}_x-0,8018\, \vec{a}_y+0,5345\, \vec{a}_z\]

Exemplo 2:
Dados os pontos $A(2, 1, 3)$ e $B(4, -2, 5)$, encontre o vetor $\vec{V}_{AB}$ e o vetor unitário $\vec{v}_{AB}$.

Solução: Para encontrar o vetor $\vec{V}_{AB}$, utilizamos a equação: \[ \vec{V}_{AB} = B - A = (4 \, \vec{a}_x - 2 \, \vec{a}_y + 5 \, \vec{a}_z) - (2 \, \vec{a}_x + 1 \, \vec{a}_y + 3 \, \vec{a}_z) \] Simplificando, obtemos: \[ \vec{V}_{AB} = 2 \, \vec{a}_x - 3 \, \vec{a}_y + 2 \, \vec{a}_z \] Para encontrar o vetor unitário $\vec{v}_{AB}$: \[ \vec{v}_{AB} = \frac{\vec{V}_{AB} }{ \vert \vec{V}_{AB} \vert } = \frac{2 \, \vec{a}_x - 3 \, \vec{a}_y + 2 \, \vec{a}_z}{\sqrt{2^2 + (-3)^2 + 2^2} } \] Após calcular o módulo: \[ |\vec{V}_{AB}| = \sqrt{4 + 9 + 4} = \sqrt{17} \approx 4,1231 \] Portanto, o vetor unitário $\vec{v}_{AB}$ será dado por: \[ \vec{v}_{AB} = \frac{2 \, \vec{a}_x - 3 \, \vec{a}_y + 2 \, \vec{k}_z}{4,1231} \approx 0,4845 \, \vec{a}_x - 0,7267 \, \vec{a}_y + 0,4845\vec{a}_z \]

Vista através de retinas atentas a matemática é simples e, muitas vezes, bela.

Exercício 2

Você é um capitão de um pequeno barco de pesca, perdido em alto mar. Sua bússola, impressa em um plano cartesiano, mostra a direção para o porto seguro como um vetor $\, \vec{a} = (4, 3, -1)$. Este vetor contém a direção e a força dos ventos e correntes que você deve enfrentar. Sua tarefa é simplificar essa informação em um vetor unitário que aponte a direção exata para o porto. Lembre-se, um vetor unitário tem magnitude $1$ e aponta na mesma direção e sentido do vetor original. Utilize suas habilidades em álgebra vetorial para encontrar esse vetor unitário e aponte seu barco para casa.

Exercício 3

Em um antigo mapa de um navegador solitário, as distâncias eram indicadas apenas por unidades, sem definição específica de sua medida, como se fossem passos ou palmos. Naqueles tempos, a precisão não era tão exigente, e os navegadores costumavam confiar em seus instintos e habilidades de observação. Nesse mapa peculiar, o navegador anotou:

1. Um trajeto que começa em seu ponto de partida, marcado como a origem, e vai até um ponto de interesse $A = (-3, 4, 5)$.
2. Um vetor unitário $b$ que, também a partir da origem, aponta na direção de um segundo ponto de interesse, $B$, e é representado por $\vec{b} = \frac{(-2, 1, 3)}{2}$.
3. Ele também fez uma anotação de que a distância entre os dois pontos de interesse, $A$ e $B$, era de 12 unidades. Talvez essa fosse a distância que ele precisava viajar em um dia para chegar ao ponto $B$ antes do anoitecer. Talvez fosse apenas um sonho, um destino que nunca foi percorrido. Não sabemos, mas talvez seja possível determinar as coordenada exatas do ponto $B$ no mapa.

Considerando as informações disponíveis, qual seria a localização exata do ponto $B$ no mapa?

Multiplicação por Escalar

Um escalar é um número, um valor, frio, simples e direto. A informação contida no escalar não precisa de direção, sentido, ou qualquer outra informação. A massa do seu navio é um valor escalar, a velocidade com que ele singra os mares é um valor vetorial.

São claramente escalares todos os números reais $(\mathbb{R})$, inteiros $(\mathbb{Z})$ ou naturais $(\mathbb{N})$. Os números complexos $(\mathbb{C})$ também são escalares. Contudo precisam de um pouco mais de atenção.

Os números complexos, $\mathbb{C}$ contém informações que podem ser associadas a direção e sentido mas, não são vetores. São como peixes em um lago. A parte real é como a distância que o peixe nada para leste ou oeste. A parte imaginária é o quanto ele nada para norte ou sul. Eles podem mover-se em duas direções, mas não são como o vento ou um rio, que têm uma direção e um sentido claros. Os números complexos, eles são mais como os peixes - nadam por aí, sem preocupação com a direção. São escalares, não vetores.

Tal como um pescador marca a posição de um peixe pelo quão longe está da margem e em que ângulo, podemos fazer o mesmo com números complexos. Chamamos de magnitude a distância até a origem e ângulo é a direção que aponta para eles. Ainda assim, não confunda isso com a direção e o sentido de um vetor na física. É uma comparação, nada mais.

É importante entender que números complexos, $\mathbb{C}$, possuem um conceito relacionado a magnitude e fase, ângulo na representação polar, em que um número complexo $c$ pode ser representado como $r*e^{i\theta}$, onde $r$ é a magnitude (ou o módulo) do número complexo, e $\theta$ é a fase (ou o argumento), que pode ser pensada como a direção do número complexo no plano complexo. Mas, novamente, o conceito de direção usado aqui não é o mesmo conceito de direção quando nos referimos a vetores. É apenas uma analogia matemática.

Sim! A matemática tem analogias.

Voltaremos aos números complexos quando for conveniente ao entendimento de fenômenos eletromagnéticos. Vamos apenas guardar em nossa caixa de ferramentas a noção de que um número, seja ele complexo, ou não, é um escalar. Uma informação de valor fundamental para o entendimento das operações com vetores.

A multiplicação de um vetor $\vec{B}$ por um escalar implica na multiplicação de cada um dos componentes $b$ desse vetor por este escalar.

Os escalares que usaremos nesta jornada serão elementos do conjunto dos números reais $\Bbb{R}$. Sem esquecer que, como vimos antes, os elementos dos conjunto dos números reais $\Bbb{R}$ são um subconjunto do conjunto dos números complexos $\Bbb{C}$ a mesma definição que utilizamos quando explicitamos as regras de formação do espaço vetorial $\mathbf{V}$ ao definirmos o universo em que estamos navegando.

A multiplicação de cada componente por um escalar é muito simples e quase não requer um exemplo. Quase.

Exemplo 3:
Considere o vetor $\, \vec{a}=2\, \vec{a}_x+4\, \vec{a}_y-\, \vec{a}_z$ e calcule $3,3\, \vec{a}$ e $\, \vec{a}/2$:

Solução: \[3,3\, \vec{a}=(3,3)(2)\, \vec{a}_x+(3,3)(4)\, \vec{a}_y+(3,3)(-1)\, \vec{a}_z\] \[3.3\, \vec{a}=6,6\, \vec{a}_x+13,2\, \vec{a}_y-3,3\, \vec{a}_z\] \[\frac{ \, \vec{a} }{2}=(\frac{1}{2})(2)\, \vec{a}_x+(\frac{1}{2})(4)\, \vec{a}_y+(\frac{1}{2})(-1)\, \vec{a}_z\] \[\frac{\, \vec{a} }{2}=\, \vec{a}_x+2\, \vec{a}_y-\frac{1}{2}\, \vec{a}_z\]

A multiplicação por escalar é comutativa, associativa, distributiva e fechada em relação ao zero e ao elemento neutro. Se tivermos os escalares $m$ e $n$ e os vetores $\, \vec{a}$ e $\vec{B}$, as propriedades da multiplicação por um escalar serão dadas por:

1. comutatividade: a ordem dos fatores não afeta o produto. Portanto, se você multiplicar um vetor por um escalar, receberá o mesmo resultado, independentemente da ordem. Ou seja, $m(\, \vec{a}) = (\, \vec{a})m$.

2. associatividade: a forma como os fatores são agrupados não afeta o produto. Portanto, se você multiplicar um vetor por um produto de escalares, receberá o mesmo resultado, independentemente de como os fatores são agrupados. Ou seja, $(mn)\, \vec{a} = m(n\, \vec{a})$.

3. distributividade: a multiplicação por escalar é distributiva em relação à adição de vetores e de escalares. Portanto, se você multiplicar a soma de dois vetores por um escalar, o resultado será o mesmo que se você multiplicar cada vetor pelo escalar e somar os resultados. Ou seja, $m(\, \vec{a} + \vec{B})=m\, \vec{a} + m\vec{B}$. Da mesma forma, se você multiplicar um vetor pela soma de dois escalares, o resultado será o mesmo que se você multiplicar o vetor por cada escalar e somar os resultados. Ou seja, $(m + n)\, \vec{a} = m\, \vec{a} + n\, \vec{a}$.

4. Fechada em relação ao zero e ao elemento neutro: Multiplicar qualquer vetor por zero resulta no vetor zero. Ou seja, $0\, \vec{a} = 0$. E multiplicar qualquer vetor por $1$ (o elemento neutro da multiplicação escalar) resulta no mesmo vetor. Ou seja, $1\, \vec{a} = \, \vec{a}$. Em resumo, teremos:

   \[m\, \vec{a}=\, \vec{a}m\] \[m(n\, \vec{a}) = (mn)\, \vec{a}\] \[m(\, \vec{a}+\vec{B}) = m\, \vec{a}+m\vec{B}\] \[(\, \vec{a}+\vec{B})n = n\, \vec{a}+n\vec{B}\] \[1\, \vec{a}=\, \vec{a}\] \[0\, \vec{a}=0\]

Vetor Oposto

A multiplicação de um vetor pelo escalar $-1$ é especial. Chamamos de vetor oposto ao vetor $\, \vec{a}$ ao vetor que tem a mesma intensidade, a mesma direção e sentido oposto ao sentido de $\, \vec{a}$. Um Vetor Oposto é o resultado da multiplicação de um vetor pelo escalar $-1$. Logo:

\[-1\, \vec{a} = -\, \vec{a}\]

Há que ser oposto. Ele se opõe a grandeza que o vetor representa. Vetores não podem ser negativos ². Não existem vetores negativos assim como não existem forças negativas. Por isso devem ser opostos, devem se opor a uma direção em um sentido.

Um vetor é uma coleção de informações, uma direção, um sentido e uma magnitude. Uma tupla com três informações, nenhuma delas pode ser negativa. Por outro lado, sabemos que forças podem ser puxões, ou empurrões. Se forem iguais em um determinado ponto, não há efeito. Como representar algo que tenha a mesma intensidade, mesma direção e sentido oposto? Usamos um sinal de negativo. Sem o vetor oposto, a aritmética entre vetores seria muito complexa, ou impossível.

Adição e Subtração de Vetores

Olhe para os pássaros no céu. Os vetores são como o rastro de um pássaro no céu, mostrando não apenas quão longe voou, mas também a direção que escolheu. Representam forças, esses ventos invisíveis que movem o mundo, que também são assim. Eles têm amplitude e direção, forças são vetores no universo da Álgebra Linear.

Como os pássaros no céu, os vetores também podem se juntar, ou se afastar. A soma, a subtração, fazem parte do seu voo. Alguns podem achar útil imaginar isso, recorrendo a geometria, como um paralelogramo, uma forma com lados paralelos que mostra como um vetor soma ao outro.

Eu não vou priorizar uma jornada pelo mundo das formas e linhas, não aqui, não agora. Mesmo assim, a amável leitora precisa lembrar que a geometria, silenciosa e imóvel, sempre estará lá, por baixo de tudo, o esqueleto do invisível que dá forma física do nosso universo. Usando um pouco de geometria, a soma de vetores, pode ser facilmente visualizada em um espaço bidimensional, um plano. Neste caso, podemos transladar os vetores envolvidos de forma a criar um paralelogramo. A diagonal maior deste paralelogramo representará a soma dos vetores.

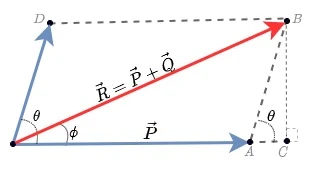
Na Figura 3, o vetor $\vec{R}$, resultante de $\vec{P}+\vec{Q}$ pode ser deduzido com a aplicação da trigonometria aplicada aos triângulos, formados pela translação dos vetores. Transladamos uma cópia de $\vec{Q}$ até o ponto $A$ e transladamos uma cópia de $\vec{P}$ até o ponto $D$, formando um paralelogramo, $OABD$.

Para determinar o vetor $\vec{R}$, criamos uma linha perfeitamente sobreposta ao vetor $\vec{P}$ que se estenda além do seu comprimento, e um segmento de reta, perfeitamente transversal a extensão do vetor $\vec{P}$ que passe pelo ponto $B$. Chamaremos este segmento de reta perpendicular de $\overline{CB}$. Neste ponto, além do paralelogramo que dá nome a regra, formamos um triângulo retângulo, $OCB$.

Considerando os segmentos de reta $\overline{OC}$, $\overline{OB}$ e $\overline{BC}$ que formam o triângulo $OCB$ e o Teorema de Pitágoras teremos:

\[\overline{OB}^2 =\overline{OC}^2 + \overline{BC}^2\]

Que pode ser escrito em uma forma mais conveniente, de dividirmos $\overline{OC}$ em dois segmentos de reta:

\[\overline{OB}^2 =(\overline{OA}+\overline{AC})^2 + \overline{BC}^2 \quad (\text{i})\]

Observando o triângulo $OCB$, e aplicando uma pitada de trigonometria podemos dizer que:

\[cos \theta = \frac{\overline{AC} }{\overline{BC} } \space\space \therefore \space\space \overline{AC} = (cos \theta) (\overline{BC})\]

Como $\overline{AB} = \overline{OD} = \vert \vec{Q} \vert $ teremos:

\[\overline{AC} = (cos \theta) ( \vert \vec{Q} \vert )\]

Este não é o único triângulo que temos. Ainda podemos trabalhar com o triângulo $ABC$. Neste caso:

\[cos \theta = \frac{\overline{BC} }{\overline{AB} } \space\space \therefore \space\space \overline{BC} = (cos \theta) (\overline{AB})\]

A paciente leitora precisa olhar esta soma com carinho e cuidado. Observe que quando encontramos a diagonal principal, encontramos também uma área. A área do paralelogramo.

A matemática irascível, nos força a dizer que o espaço vetorial $\mathbf{V}$ é fechado em relação a soma de vetores. Forma direta de dizer que a soma de dois vetores do espaço $\mathbf{V}$ resulta em um vetor deste mesmo espaço. Fechamento é um conceito da álgebra, e determina quais operações binárias que aplicadas os elementos de um conjunto, resultam em elementos deste mesmo conjunto.

Limitados como estamos pela Álgebra Linear, veremos que a soma de vetores em um dado espaço vetorial será feita componente a componente. Se considerarmos os vetores $\vec{A}$ e $\vec{B}$ poderemos encontrar um vetor $\vec{C}$ que será a soma de $\vec{A}$ e $\vec{B}$ representada por $\vec{C}=\vec{A}+\vec{B}$ por:

\[\vec{C}= \vec{A}+\vec{B}=(\, \vec{a}_x \, \vec{a}_x+\, \vec{a}_y \, \vec{a}_y+\, \vec{a}_z \, \vec{a}_z)+(B_x \, \vec{a}_x+B_y \, \vec{a}_y+B_z \, \vec{a}_z)\] \[\vec{C}=\vec{A}+\vec{B}=(\, \vec{a}_x+B_x)\, \vec{a}_x+(\, \vec{a}_y+B_y)\, \vec{a}_y+(\, \vec{a}_y+B_y)\, \vec{a}_z\]

Exemplo 4:
Se \vec{A}=5\vec{a}_x-3\, \vec{a}_y+\, \vec{a}_z$ e $\vec{B}=\, \vec{a}_x+4\, \vec{a}_y-7\, \vec{a}_z$. Calcule $\vec{C}=vec{A}+\vec{B}$.

Solução \[\vec{C}=\vec{A}+\vec{B}=(5\, \vec{a}_x-3\, \vec{a}_y+\, \vec{a}_z)+(1\, \vec{a}_x+4\, \vec{a}_y-7\, \vec{a}_z)\] \[\vec{C}=\vec{A}+\vec{B}=(5+1)\, \vec{a}_x+(-3+4)\, \vec{a}_y+(1-7)\, \vec{a}_z \] \[\vec{C}= 6\, \vec{a}_x+\, \vec{a}_y-6\, \vec{a}_z\]

Exemplo 5:
Dado o vetor $\vec{A} = 4 \, \vec{a}_x + 6 \, \vec{a}_y + 3 \, \vec{a}_z$ e o vetor $\vec{B} = 3 \, \vec{a}_x - 2\vec{a}_y + 8 \, \vec{a_z}$, a projeção do vetor soma $\vec{C}=\vec{A}+\vec{B}$ sobre o eixo $y$ será: .

Solução Para descobrir essa projeção, precisamos efetuar a soma $\vec{C}=\vec{A}+\vec{B}$: \[ \vec{C}=\vec{A}+\vec{B} = (4 + 3) \, \vec{a}_x + (6 - 2) \, \vec{a}_y + (3 + 8) \, \vec{a}_z = 7 \, \vec{a}_x + 4 \, \vec{a}_y + 11 \, \vec{a}_z \] Lembrando que os componentes do vetor são, na verdade, a projeção do vetor em cada um dos eixos do sistema de coordenadas, a projeção sobre o eixo $y$ será: $4$.

Recorrendo ao auxílio da aritmética dos números escalares, podemos dizer que: a subtração entre dois vetores também será uma soma. Desta feita, uma soma entre um vetor e o vetor oposto de outro vetor Assim:

\[\vec{C}=\vec{A}-\vec{B}=\vec{A}+(-\vec{B})=\vec{A}+(-1\vec{B})\]

Talvez um exemplo ajude a amável leitora a perceber que, vetorialmente, até quando subtraímos estamos somando.

Exemplo 6:
Considere $\vec{A}=\vec{a}_x-3\, \vec{a}_y+\, \vec{a}_z$ e $\vec{B}=1\, \vec{a}_x+4\, \vec{a}_y-7\, \vec{a}_z$ e calcule $\vec{C}=\, \vec{a}-\vec{B}$.

Solução: \[\vec{C}=\vec{A}-\vec{B}=(5\, \vec{a}_x-3\, \vec{a}_y+\, \vec{a}_z)+(-1(1\, \vec{a}_x+4\, \vec{a}_y-7\, \vec{a}_z))\] \[\vec{C}=\vec{A}-\vec{B}=(5\, \vec{a}_x-3\, \vec{a}_y+\, \vec{a}_z)+(-1\, \vec{a}_x-4\, \vec{a}_y+7\, \vec{a}_z)\] \[\vec{C}=\vec{A}-\vec{B}=4\, \vec{a}_x-7\, \vec{a}_y+8\, \vec{a}_z\]

A consistência ressalta a beleza da matemática. As operações de adição e subtração de vetores obedecem a um conjunto de propriedades matemáticas que garantem a consistência destas operações. Para tanto, considere os vetores $\vec{A}$, $\vec{B}$ e $\vec{B}$, e o escalar $m$:

1. comutatividade da adição de vetores: a ordem dos vetores na adição não afeta o Resultado. Portanto, $\vec{A} + \vec{B} = \vec{B} + \, \vec{a}$. A subtração, entretanto, não é comutativa, ou seja, $\vec{A} - \vec{B} ≠ \vec{B} - \vec{A}$. A comutatividade é como uma dança onde a ordem dos parceiros não importa. Neste caso, subtrair não é como dançar e a ordem importa.

2. associatividade da adição de vetores: a forma como os vetores são agrupados na adição não afeta o Resultado. Assim, $(\vec{A} + \vec{B}) + \vec{C} = \vec{A} + (\vec{B} + \vec{C})$. A associatividade é como um grupo de amigos que se reúne. Não importa a ordem de chegada o resultado é uma festa. A subtração, entretanto, não é associativa, ou seja, $(\vec{A} - \vec{B}) - \vec{C} ≠ \vec{A} - (\vec{B} - \vec{C})$.

3. Distributividade da multiplicação por escalar em relação à adição de vetores: Se você multiplicar a soma de dois vetores por um escalar, o resultado será o mesmo que se você multiplicar cada vetor pelo escalar e somar os resultados. Isto é, $m(\vec{A} + \vec{B}) = m\vec{A} + m\vec{B}$.

Essas propriedades são fundamentais para a manipulação de vetores em muitas áreas da física e da matemática e podem ser resumidas por:

\[\vec{A}+\vec{B}=\vec{B}+\vec{A}\] \[\vec{A}+(\vec{B}+\vec{C})=(\vec{A}+\vec{B})+\vec{C}\] \[m(\vec{A}+\vec{B})=m\vec{A}+m\vec{C}\]

Importante: a subtração não é comutativa nem associativa. Logo:

\[\vec{A} - \vec{B} ≠ \vec{B} - \vec{A}\] \[(\vec{A} - \vec{B}) - \vec{C} ≠ \vec{A} - (\vec{B} - \vec{C})\]

Exercício 4

Alice é uma engenheira trabalhando no projeto de construção de uma ponte. As forças aplicadas sobre um pilar foram simplificadas até que serem reduzidas a dois vetores: $\vec{F}_1 = 4\, \vec{a}_x + 3\, \vec{a}_y$ e $\vec{F}_2 = -1\, \vec{a}_x + 2\, \vec{a}_y$ a força aplicada ao pilar será o resultado da subtração entre os vetores. Alice precisa saber qual será a força resultante após aplicar uma correção de segurança ao vetor $\vec{F}_2$ multiplicando-o por $2$. O trabalho de Alice é definir as características físicas deste pilar, o seu é ajudar Alice com estes cálculos.

Exercício 5

Larissa é uma física estudando o movimento de uma partícula em um campo elétrico. Ela reduziu o problema a dois vetores representando as velocidades da partícula em um momento específico: $\vec{V}_1 = 6\, \vec{a}_x - 4\, \vec{a}_y + 2\, \vec{a}_z$ e $\vec{V}_2 = 12\, \vec{a}_x + 8\, \vec{a}_y - 4\, \vec{a}_z$. Larissa precisa qual será a velocidade média da partícula se ele considerar que $\vec{V}_2$ deve ser dividido por $2$ graças ao efeito de uma força estranha ao sistema agindo sobre uma das partículas. Para ajudar Larissa ajude-a a determinar a velocidade média, sabendo que esta será dada pela soma destes vetores após a correção dos efeitos da força estranha ao sistema.

Exercício 6

Marcela é uma física experimental realizando um experimento em um laboratório de pesquisas em um projeto para estudar o movimento de partículas subatômicas. As velocidades das partículas $A$ e $B$ são representadas pelos vetores $\vec{v}_A$ e $\vec{v}_B$, definidos por:

\[\vec{v}_A = -10\, \vec{a}_x + 4\, \vec{a}_y - 8\, \vec{a}_z \, \text{m/s}\] \[\vec{v}_B = 8\, \vec{a}_x + 7\, \vec{a}_y - 2\, \vec{a}_z \, \text{m/s}\]

Marcela precisa calcular a velocidade resultante $\vec{v}_R$ das partículas $A$ e $B$ sabendo que neste ambiente os as velocidades das partículas são afetadas por forças provenientes de campos externos que foram modeladas na equação $\vec{v}_R = 3\vec{v}_A - 4\vec{v}_B$. Qual o vetor unitário que determina a direção e o sentido de $\vec{v}_R$ nestas condições?

Exercício 7

Tudo é relativo! A amável leitora já deve ter ouvido esta frase. Uma mentira, das mais vis deste nossos tempos. Tudo é relativo, na física! Seria mais honesto. Não existe qualquer documento, artigo, livro, ou entrevista onde Einstein tenha dito tal sandice. Ainda assim, isso é repetido a exaustão. Não por nós. Nós dois estamos em busca da verdade do conhecimento. E aqui, neste ponto, entra o conceito de Einstein: as leis da física são as mesmas independente do observador. Isso quer dizer que, para entender um fenômeno, precisamos criar uma relação entre o observador e o fenômeno. Dito isso, considere que você está observando um trem que corta da direita para esquerda seu campo de visão em velocidade constante $\vec{V}_t = 10 \text{km/h}$. Nesse trem, um passageiro atravessa o vagão perpendicularmente ao movimento do trem em uma velocidade dada por $\vec{V}_p = 2 \text{km/h}$. Qual a velocidade deste passageiro para você, que está colocada de forma perfeitamente perpendicular ao movimento do trem?

Exercício 8

Vamos tornar o exercício 7 mais interessante: considere que você está observando um trem que corta da direita para esquerda seu campo de visão em velocidade constante $\vec{V}_t = 10 \text{km/h}$ subindo uma ladeira com inclinação de $25^\circ$. Nesse trem, um passageiro atravessa o vagão perpendicularmente ao movimento do trem em uma velocidade dada por $\vec{V}_p = 2 \text{km/h}$. Qual a velocidade deste passageiro para você, que está colocada de forma perfeitamente perpendicular ao movimento do trem?

Vetores Posição e Distância

Um vetor posição, ou vetor ponto, é uma ferramenta útil para descrever a posição de um ponto no espaço em relação a um ponto de referência (geralmente a origem do sistema de coordenadas). Como uma flecha que começa na origem, o coração do sistema de coordenadas, onde $x$, $y$, e $z$ são todos zero, $(0,0,0)$, e termina em um ponto $P$ no espaço. Este ponto $P$ tem suas próprias coordenadas - digamos, $x$, $y$, e $z$.

O vetor posição $\vec{R}$ que vai da origem até este ponto $P$ será representado por $\vec{R}_P$. Se as coordenadas de $P$ são $(x, y, z)$, então o vetor posição $\vec{R}_P$ será:

\[\vec{R}_p = x\, \vec{a}_x + y\, \vec{a}_y + z\, \vec{a}_z\]

O que temos aprendido, na nossa jornada, até o momento, sobre vetores é simplesmente uma forma diferente de olhar para a mesma coisa. Sem nenhuma explicitação específica, estamos usando o conceito de Vetor Posição, desde que começamos este texto.

A soma de vetores unitários, $\vec{a}_x$, $\vec{a}_y$, $\vec{a}_z$, que define um vetor em qualquer direção que escolhemos, sob um olhar alternativo irá definir o Vetor Posição de um dado ponto no espaço. Isso é possível porque, neste caso, estamos consideramos o vetor como uma seta que parte do zero - a origem - e se estende até qualquer ponto no espaço.

Como a doce leitora pode ver, está tudo conectado, cada parte fazendo sentido à luz da outra. Assim, aprenderemos a entender o espaço ao nosso redor, uma vetor de cada vez.

No universo dos problemas reais, onde estaremos sujeitos a forças na forma de gravidade, eletromagnetismo, ventos e correntes. Não podemos nos limitar a origem como ponto de partida de todos os vetores. Se fizermos isso, corremos o risco de tornar complexo o que é simples.

Na frieza da realidade, entre dois pontos quaisquer no espaço, $P$ e $Q$ será possível traçar um vetor. Um vetor que chamaremos de vetor distância e representaremos por $\vec{R}$.

Dois pontos no espaço, $P$ e $Q$, são como dois pontos num mapa. Cada um tem seu próprio vetor posição - seu próprio caminho da origem, o centro do mapa, até onde eles estão. Chamamos esses caminhos de $\vec{R}_P$ e $\vec{R}_Q$. Linhas retas que partem da origem, o centro do mapa e chegam a $P$ e $Q$. Usando para definir estes pontos os vetores posição a partir da origem.

Agora, se você quiser encontrar a distância entre $P$ e $Q$, não o caminho do centro do mapa até $P$ ou $Q$, mas o caminho direto partindo de $P$ até $Q$. Este caminho será o vetor distância $\vec{R}_{PQ}$.

Resta uma questão como encontramos $\vec{R}_{PQ}$?

Usamos a subtração de vetores. O vetor distância $\vec{R}_{PQ}$ será a diferença entre $\vec{R}_Q$ e $\vec{R}_P$. É como pegar o caminho de $Q$ ao centro do mapa, a origem do Sistema de Coordenadas Cartesianas, e subtrair o caminho de $P$ a este mesmo ponto. O que sobra é o caminho de $P$ até $Q$.

\[\vec{R} = \vec{R}_Q - \vec{R}_P\]

$\vec{R}$, a distância entre $P$ e $Q$, será geometricamente representado por uma seta apontando de $P$ para $Q$. O comprimento dessa seta é a distância entre $P$ e $Q$. Ou, em outras palavras, se temos um vetor, com origem em um ponto $P$ e destino em um ponto $Q$ a distância entre estes dois pontos será a magnitude deste vetor. E agora a amável leitora sabe porque chamamos de vetor posição ao vetor resultante a subtração entre dois vetores com origem no mesmo ponto.

É um conceito simples, porém poderoso. Uma forma de conectar dois pontos em um espaço, uma forma de enxergar todo espaço a partir dos seus pontos e vetores. Definindo qualquer vetor a partir dos vetores posição. Bastando para tanto, definir um ponto comum para todo o espaço. Coisa que os sistemas de coordenadas fazem por nós graciosamente.

Exemplo: 7
Considerando que $P$ esteja nas coordenadas $(3,2,-1)$ e $Q$ esteja nas coordenadas $(1,-2,3)$. Logo, o vetor distância $\vec{R}_{PQ}$ será dado por:

Solução: \[\vec{R}_{PQ} = \vec{R}_P - \vec{R}_Q\] Logo: \[\vec{R}_{PQ} = (P_x-Q_x)\, \vec{a}_x + (P_y-Q_y)\, \vec{a}_y+(P_z-Q_z)\, \vec{a}_z\] \[\vec{R}_{PQ} = (3-1)\, \vec{a}_x+(3-(-2))\, \vec{a}_y+((-1)-3)\, \vec{a}_z\] \[\vec{R}_{PQ} = 2\, \vec{a}_x+5\, \vec{a}_y-4\, \vec{a}_z\]

Exemplo 8:
Dados os pontos $P_1(4,4,3)$, $P_2(-2,0,5)$ e $P_3(7,-2,1)$. (a) Especifique o vetor $\, \vec{a}$ que se estende da origem até o ponto $P_1$. (b) Determine um vetor unitário que parte da origem e atinge o ponto médio do segmento de reta formado pelos pontos $P_1$ e $P_2$. (c) Calcule o perímetro do triângulo formado pelos pontos $P_1$, $P_2$ e $P_3$.

Solução:
(a) o vetor $\, \vec{a}$ será o vetor posição do ponto $P_1(4,3,2)$ dado por: $$\, \vec{a} = 4\, \vec{a}_x+4\, \vec{a}_y+3\, \vec{a}_z$$ (b) para determinar um vetor unitário que parte da origem e atinge o ponto médio do segmento de reta formado pelos pontos $P_1$ e $P_2$ precisamos primeiro encontrar este ponto médio $P_M$. Então: \[P_M=\frac{P_1+P_2}{2} =\frac{(4,4,3)+(-2,0,5)}{2}\] \[P_M=\frac{(2,4,8)}{2} = (1, 2, 4)\] \[P_M=\, \vec{a}_x+2\, \vec{a}_y+4\, \vec{a}_z\] Para calcular o vetor unitário na direção do vetor $P_M$ teremos: \[\vec{a}\_{P_M}=\frac{(1, 2, 4)}{|(1, 2, 4)|} = \frac{(1, 3, 4)}{\sqrt{1^2+2^2+4^2} }\] \[\vec{a}\_{P_M}=0.22\, \vec{a}_x+0.45\, \vec{a}_y+0.87\, \vec{a}_z\] (c) finalmente, para calcular o perímetro do triângulo formado por: $P_1(4,4,3)$, $P_2(-2,0,5)$ e $P_3(7,-2,1)$, precisaremos somar os módulos dos vetores distância ente $P_1(4,3,2)$ e $P_2(-2,0,5)$, $P_2(-2,0,5)$ e $P_3(7,-2,1)$ e $P_3(7,-2,1)$ e $P_1(4,3,2)$. \[ \vert P_1P_2 \vert = \vert (4,4,3)-(-2,0,5) \vert = \vert (6,4,-2) \vert \] \[ \vert P_1P_2 \vert = \sqrt{6^2+4^2+2^2}=7,48\] \[ \vert P_2P_3 \vert = \vert (-2,0,5)-(7,-2,1) \vert = \vert (-9,2,-4) \vert \] \[ \vert P_2P_3 \vert = \sqrt{9^2+2^2+4^2}=10,05\] \[ \vert P_3P_1 \vert = \vert (7,-2,1)-(4,4,3) \vert = \vert (3,-6,-2) \vert \] \[ \vert P_3P_1 \vert = \sqrt{3^2+6^2+6^2}=7\] Sendo assim o perímetro será: \[ \vert P_1P_2 \vert + \vert P_2P_3 \vert + \vert P_3P_1 \vert =7,48+10,05+7=24.53 \]

Vetores são como os ventos que cruzam o mar, invisíveis mas poderosos, guiando navios e direcionando correntes. Na matemática, eles têm sua própria linguagem, um código entre o visível e o invisível, mapeando direções e magnitudes. Aqui, você encontrará exercícios que irão desafiar sua habilidade de navegar por esse oceano numérico. Não são apenas problemas, mas bússolas que apontam para o entendimento mais profundo. Então pegue lápis e papel como se fossem um leme e um mapa e prepare-se para traçar seu próprio curso.

Exercício 9

Considere um sistema de referência onde as distâncias são dimensionadas apenas por unidades abstratas, sem especificação de unidades de medida. Nesse sistema, dois vetores são dados. O vetor $\vec{A}$ inicia na origem e termina no ponto $P$ com coordenadas $(8, -1, -5)$. Temos também um vetor unitário $\vec{c}$ que parte da origem em direção ao ponto $Q$, e é representado por $\frac{1}{3}(1, -3, 2)$. Se a distância entre os pontos $P$ e $Q$ é igual a 15 unidades, determine as coordenadas do ponto $Q$.

Exercício 10

Considere os pontos $P$ e $Q$ localizados em $(1, 3, 2)$ e $(4, 0, -1)$, respectivamente. Calcule: (a) O vetor posição $\vec{P}$; (b) O vetor distância de $P$ para $Q$, $\vec{PQ}$; (c) A distância entre $P$ e $Q$; (d) Um vetor paralelo a $\vec{PQ}$ com magnitude de 10.

Produto Escalar

Há um jeito de juntar dois vetores - setas no espaço - e obter algo diferente: um número, algo mais simples, sem direção, sem sentido, direto e frio. Este é o Produto Escalar. O resultado do Produto Escalar entre dois vetores é um valor escalar.

A operação Produto Escalar recebe dois vetores e resulta em um número que, no espaço vetorial $\textbf{V}$, definido anteriormente, será um número real. Esse resultado tem algo especial: sua invariância. Não importa a orientação, rotação ou o giro que você imponha ao espaço vetorial, o resultado do Produto Escalar, continuará imutável, inalterado.

A amável leitora há de me perdoar, mas é preciso lembrar que escalares são quantidades que não precisam saber para onde estão apontando. Elas apenas são. Um exemplo? A Temperatura. Não importa como você oriente, gire ou mova um sistema de coordenadas aplicado no espaço para entender um fenômeno termodinâmico, a temperatura deste sistema permanecerá a mesma. A temperatura é uma quantidade que não tem direção nem sentido.

Aqui está o pulo da onça: enquanto um vetor é uma entidade direcionada, seus componentes são meros escalares. Ao decompor um vetor em seus componentes unitários — cada qual seguindo a direção de um eixo coordenado — é preciso entender que esses elementos são fluidos e mutáveis dependem das características do sistema de coordenadas. Os componentes se ajustam, se transformam e se adaptam quando você roda ou reorienta o espaço. Em contraste, o Produto Escalar, apesar de sua simplicidade, permanece constante, imperturbável às mudanças espaciais. Ele é um pilar invariável, vital para compreender tanto a estrutura do espaço quanto as dinâmicas que nele ocorrem.

Usando a linguagem da matemática, direta e linda, podemos dizer que dados os vetores $\vec{A}$ e $\vec{B}$, o Produto Escalar entre $\vec{A}$ e $\vec{B}$ resultará em uma quantidade escalar. Esta operação será representada, usando a linguagem da matemática, por $\vec{A}\cdot \vec{B}$.

Aqui abro mão da isenção e recorro a geometria. Mais que isso, faremos uso da trigonometria para reduzir o Produto Escalar ao máximo de simplicidade usando uma equação que inclua o ângulo entre os dois vetores. Sem nos perdermos nas intrincadas transformações trigonométricas diremos que o Produto Escalar entre $\vec{A}$ e $\vec{B}$ será:

\[\vec{A} \cdot \vec{B} = \vert \vec{A} \vert \vert \vec{B} \vert cos(\theta_{AB})\]

Onde $\theta_{AB}$ representa o ângulo entre os dois vetores. Esta é a equação analítica do Produto Escalar. A ferramenta mais simples que podemos usar. Não é uma equação qualquer, ela representa a projeção do vetor $\vec{A}$ sobre o vetor $\vec{B}$. Se não, a paciente leitora, não estiver vendo esta projeção deve voltar a geometria, não a acompanharei nesta viagem, tenho certeza do seu sucesso. Em bom português dizemos que o Produto Escalar entre dois vetores $\vec{A}$ e $\vec{B}$ quaisquer é o produto entre o produto das magnitudes destes vetores e o cosseno do menor ângulo entre eles.

Vetores são como flechas atiradas no vazio do espaço. E como flechas, podem seguir diferentes caminhos.

Alguns vetores correm paralelos, como flechas lançadas lado a lado, nunca se encontrando. Eles seguem a mesma direção, compartilham o mesmo curso, mas nunca se cruzam. Sua jornada é sempre paralela, sempre ao lado. O ângulo entre eles, $\theta$, é $\text{zero}$ neste caso o cosseno entre eles, $cos(\theta)$ será então $1$. E o Produto Escalar entre eles será o resultado do produto entre suas magnitudes.

Outros vetores são transversais, como flechas que cortam o espaço em ângulos retos, ângulos $\theta = 90^\circ$. Eles não seguem a mesma direção, nem o mesmo caminho. Eles se interceptam, mas em ângulos precisos, limpos, cortando o espaço como uma grade. O cosseno entre estes vetores é $0$. E o Produto Escalar será zero independente das suas magnitudes.

Entre os vetores que correm em paralelo e aqueles que se cruzam transversalmente estão os limites superior e inferior do Produto Escalar, seu valor máximo e mínimo. Estes são os vetores que se cruzam em qualquer ângulo, como flechas lançadas de pontos distintos, cruzando o espaço de formas únicas. Eles podem se encontrar, cruzar caminhos em um único ponto, ou talvez nunca se cruzem. Estes vetores desenham no espaço uma dança de possibilidades, um balé de encontros e desencontros. Aqui, o cosseno não pode ser determinado antes de conhecermos os vetores em profundidade. Para estes rebeldes, usamos o ângulo mínimo entre eles. Um ângulo agudo. Quando dois vetores se cruzam, dois ângulos são criados. Para o Produto Escalar usaremos sempre o menor deles, o ângulo, mínimo, interno deste relacionamento.

Como flechas no espaço, vetores desenham caminhos - paralelos, transversais ou se cruzando em qualquer ângulo. Vetores são a linguagem das forças no espaço, a escrita das distâncias e direções. Eles são os contadores de histórias do espaço tridimensional.

A matemática da Álgebra Vetorial destila estes conceitos simplesmente como: se temos um vetor $\, \vec{a}$ e um vetor $\vec{B}$ teremos o Produto Escalar entre eles dado por:

\[\vec{A}\cdot \vec{B} = A_xB_x+ A_yB_y+ A_zB_z\]

Seremos então capazes de abandonar a equação analítica, e voltarmos aos mares tranquilos de ventos suaves da Álgebra Linear. A matemática nos transmite paz e segurança. Exceto quando estamos aprendendo. Nestes momentos, nada como uma xícara de chá morno e um exemplo para acender a luz do entendimento.

Exemplo 9:
Dados os vetores $\vec{A}=3\, \vec{a}_x + 4\, \vec{a}_y + \, \vec{a}_z$ e $\vec{B}=\, \vec{a}_x+2\, \vec{a}_y-5\, \vec{a}_z$ encontre o ângulo $\theta$ entre $\, \vec{a}$ e $\vec{B}$.

Solução:
Para calcular o ângulo vamos usar a equação analítica do Produto Escalar: \[\vec{A}\cdot \vec{B} = \vert \vec{a} \vert \vert \vec{B} \vert cos(\theta)\] Precisaremos dos módulos dos vetores e do Produto Escalar entre eles. Calculando o Produto Escalar a partir dos componentes vetoriais de cada vetor teremos: \[\vec{A}\cdot \vec{B} = (3,4,1)\cdot(1,2,-5) \] \[\vec{A}\cdot \vec{B} = (3)(1)+(4)(2)+(1)(-5)=6\] Calculando os módulos de $\vec{A}$ e $\vec{B}$, teremos: \[ \vert \vec{A} \vert = \vert (3,4,1) \vert =\sqrt{3^2+4^2+1^2}=5,1\] \[ \vert \vec{B} \vert = \vert (1,2,-5) \vert =\sqrt{1^2+2^2+5^2}=5,48\] Já que temos o Produto Escalar e os módulos dos vetores podemos aplicar nossa equação analítica: \[ \vec{A}\cdot \vec{B} = \vert \vec{A} \vert \vert \vec{B} \vert cos(\theta)\] logo: \[ 6 =(5,1)(5,48)cos(\theta) \therefore cos(\theta) = \frac{6}{27,95}=0,2147 \] \[ \theta = arccos(0,2147)=77,6^\circ \]

Até agora, estivemos estudando um espaço de três dimensões, traçando vetores que se projetam em comprimentos, larguras e alturas do Espaço Cartesiano. Isso serve para algumas coisas. Para resolver alguns dos problemas que encontramos na dança de forças e campos que tecem o tecido do mundo físico. Mas nem sempre é o bastante.

A verdade é que o universo é mais complexo do que as três dimensões que podemos tocar e ver. Há mundos além deste, mundos que não podemos ver, não podemos tocar, mas podemos imaginar. Para esses mundos, precisamos de mais. Muito mais.

Álgebra vetorial é a ferramenta que usamos para desenhar mundos. Com ela, podemos expandir nosso pensamento para além das três dimensões, para espaços de muitas dimensões. Espaços que são mais estranhos, mais complicados, mas também mais ricos em possibilidades. Talvez seja hora de reescrever nossa definição de Produto Vetorial, a hora de expandir horizontes. Não apenas para o espaço tridimensional, mas para todos os espaços que podem existir. Isso é o que a álgebra vetorial é: uma linguagem para desenhar mundos, de três dimensões ou mais.

Generalizando o Produto Escalar entre dois vetores $\vec{A}$ e $\vec{B}$ com $N$ dimensões teremos:

\[\vec{A} \cdot \vec{B} = \sum\limits_{i=1}\limits^{N} \vec{A}_i\vec{b}_i\]

Onde $i$ é o número de dimensões. Assim, se $i=3$ e chamarmos estas dimensões $x$, $y$, $z$ respectivamente para $i=1$, $i=2$ e $i=3$ teremos:

\[\vec{A} \cdot \vec{B} = \sum\limits_{i=1}\limits^{3} \vec{a}_i\vec{b}_i = a_1b_1 +a_2b_2 + a_3b_3\]

Ou, substituindo os nomes das dimensões:

\[\vec{A} \cdot \vec{B} = \, \vec{a}_x\vec{b}_x +\, \vec{a}_y\vec{b}_y + \, \vec{a}_z\vec{b}_z\]

Não vamos usar dimensões maiores que $3$ neste estudo. Contudo, achei que a gentil leitora deveria perceber esta generalização. No futuro, em outras disciplinas, certamente irá me entender.

Exercício 11

Em um novo projeto de engenharia civil para a construção de uma estrutura triangular inovadora, foram demarcados três pontos principais para as fundações. Esses pontos, determinados por estudos topográficos e geotécnicos, foram identificados como $A(4, 0, 3)$, $B(-2, 3, -4)$ e $C(1, 3, 1)$ em um espaço tridimensional utilizando o Sistema de Coordenadas Cartesianas. A equipe de engenheiros precisa compreender a relação espacial entre esses pontos, pois isto impacta diretamente na distribuição das cargas e na estabilidade da estrutura.

Seu desafio será determinar o o ângulo $\theta_{BAC}$ entre estes vetores para a análise estrutural, pois determina o direcionamento das forças na fundação.

Uma vez que tenhamos entendido a operação Produto Escalar, nos resta entender suas propriedades:

1. Comutatividade: o Produto Escalar tem uma beleza simples quase rítmica. Como a batida de um tambor ou o toque de um sino, ele se mantém o mesmo não importa a ordem. Troque os vetores - a seta de $\vec{A}$ para $\vec{B}$ ou a flecha de $\vec{B}$ para $\vec{A}$ - e você obtém o mesmo número, o mesmo escalar. Isso é o que significa ser comutativo. Ou seja: $\vec{A} \cdot \vec{B} = \vec{B}\cdot \vec{A}$

2. Distributividade em Relação a Adição: o Produto Escalar também é como um rio dividindo-se em afluentes. Você pode distribuí-lo, espalhá-lo, dividir um vetor por muitos. Adicione dois vetores e multiplique-os por um terceiro - você pode fazer isso de uma vez ou pode fazer um por vez. O Produto Escalar não se importa. Ele dá o mesmo número, a mesma resposta. Isso é ser distributivo em relação a adição. Dessa forma teremos: $\vec{A}\cdot (\vec{B}+\vec{C}) = \vec{A}\cdot \vec{B} + \vec{A}\cdot \vec{C}$.

3. Associatividade com Escalares: o Produto Escalar é como um maestro habilidoso que sabe equilibrar todos os instrumentos em uma orquestra. Imagine um escalar como a intensidade da música: aumente ou diminua, e a harmonia ainda será mantida. Multiplicar um vetor por um escalar e, em seguida, realizar o Produto Escalar com outro vetor é o mesmo que primeiro executar o Produto Escalar e depois ajustar a intensidade. O Produto Escalar, em sua elegância matemática, garante que o show continue de forma harmoniosa, independentemente de quando a intensidade é ajustada. Essa é a essência da associatividade com escalares. Portanto, podemos dizer que: $k(\vec{A} \cdot \vec{B}) = (k \vec{A}) \cdot \vec{B} = \vec{A} \cdot (k\vec{B})$

4. Produto Escalar do Vetor Consigo Mesmo: O Produto Escalar tem um momento introspectivo, como um dançarino girando em um reflexo de espelho. Quando um vetor é multiplicado por si mesmo, ele revela sua verdadeira força, sua magnitude ao quadrado. É uma dança solitária, onde o vetor se alinha perfeitamente consigo mesmo, na mais pura sintonia. Esta auto-referência nos mostra o quanto o vetor se projeta em sua própria direção, revelando a essência de sua magnitude. Assim, temos: $\vec{A} \cdot \vec{A} = \vert \vec{A} \vert ^2$. Veja um vetor $\vec{A}$. Uma seta solitária estendendo-se no espaço. Imagine colocar outra seta exatamente igual, exatamente no mesmo lugar. Duas Setas juntas, $\vec{A}$ e $\vec{A}$, sem nenhum ângulo entre elas.

Por que? Porque o ângulo $\theta$ entre um vetor e ele mesmo é $zero$. E o cosseno de zero é $1$. Assim:

\[\vec{A}\cdot \vec{A} = \vert \vec{A} \vert ^2\]

Para simplificar, vamos dizer que $\vec{A}^2$ é o mesmo que $ \vert \vec{A} \vert ^2$. Uma notação, uma abreviação para o comprimento, magnitude, de $\vec{A}$ ao quadrado. Aqui está a lição: um vetor e ele mesmo, lado a lado, são definidos pela magnitude do próprio vetor, ao quadrado. É um pequeno pedaço de sabedoria, um truque, uma ferramenta. Mantenha esta ferramenta sempre à mão, você vai precisar.

Assim como as ondas em uma praia, indo e voltando, de tempos em tempos precisamos rever as ferramentas que adquirimos e o conhecimento que construímos com elas. Em todos os sistemas de coordenadas que usamos para definir o espaço $\mathbf{V}$ os vetores unitários são ortogonais. Setas no espaço que se cruzam em um ângulo reto. Este ângulo reto garante duas propriedades interessantes.

\[\vec{a}_x\cdot \, \vec{a}_y=\, \vec{a}_x\cdot \, \vec{a}_z=\, \vec{a}_y\cdot \, \vec{a}_z=0\] \[\vec{a}_x\cdot \, \vec{a}_x=\, \vec{a}_y\cdot \, \vec{a}_y=\, \vec{a}_z\cdot \, \vec{a}_z=1\]

A primeira garante que o Produto Escalar entre quaisquer dois componentes vetoriais ortogonais é $zero$, a segunda que o Produto Escalar entre os mesmos dois componentes vetoriais é $1$. Essas são duas verdades que podemos segurar firmes enquanto navegamos pelo oceano do espaço vetorial. Como um farol em uma noite tempestuosa, elas nos guiarão e nos ajudarão a entender o indescritível. Mais que isso, serão as ferramentas que usaremos para transformar o muito difícil em muito fácil.

Desculpe-me! Esta ambição que me força a olhar além me guia aos limites do possível. Assim como expandimos o número de dimensões para perceber que o impacto do Produto Vetorial se estende além dos limites da nossa, precisamos, novamente, levar as dimensões do nosso universo ao ilimitável.

As propriedades derivadas da ortogonalidade dos componentes dos sistemas de coordenadas podem ser expressas usando o Delta de Kronecker definido por Leopold Kronecker(1823–1891). O Delta de Kronecker é uma forma de representar por índices as dimensões do espaço vetorial, uma generalização, para levarmos a Álgebra Linear ao seu potencial máximo, sem abandonar os limites que definimos para o estudo do Eletromagnetismo. sem delongas, teremos:

\[\begin{equation} \delta_{\mu \upsilon}=\begin{cases} 1, se \space\space \mu = \upsilon .\\ 0, se \space\space \mu \neq \upsilon. \end{cases} \end{equation}\]

Usando o Delta de Kronecker podemos escrever as propriedades dos componentes ortogonais unitários em relação ao Produto Escalar como:

\[\vec{a}_\mu \cdot \, \vec{a}_\upsilon = \delta_{\mu \upsilon}\]

Que será útil na representação computacional de vetores e no entendimento de transformações vetoriais em espaços com mais de $3$ dimensões. Que, infelizmente, estão além deste ponto na nossa jornada. Não se deixe abater, ficaremos limitados a $3$ dimensões. Contudo, não nos limitaremos ao Produto Escalar. Outras maravilhas virão.

Exemplo 10:
Dados os vetores $\vec{A} = (3, 2, 1)$ e $\vec{B} = (1, -4, 2)$, calcule o Produto Escalar $\vec{A} \cdot \vec{B}$ e também $\vec{B} \cdot \vec{A}$. Verifique a propriedade da comutatividade.

Solução:
Tudo que precisamos para provar a comutatividade é fazer o Produto Escalar em duas ordens diferentes em busca de resultados iguais. \[ \vec{A} \cdot \vec{B} = 3 \times 1 + 2 \times (-4) + 1 \times 2 = 3 - 8 + 2 = -3 \] \[ \vec{B} \cdot \vec{A} = 1 \times 3 + (-4) \times 2 + 2 \times 1 = 3 - 8 + 2 = -3\]

Exemplo 11:
Dados os vetores $\vec{A} = (2, 3, 1)$, $\vec{B} = (1, 2, 0)$ e $\vec{C} = (3, 1, 3)$, calcule $\vec{A} \cdot (\vec{B} + \vec{C})$ e compare com $\vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C}$.

Solução:
Primeiro, encontre $\vec{B} + \vec{C} = (1+3, 2+1, 0+3) = (4, 3, 3)$. \[ \vec{A} \cdot (\vec{B} + \vec{C}) = 2 \times 4 + 3 \times 3 + 1 \times 3 = 8 + 9 + 3 = 20\] \[ \vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C} = 2 \times 1 + 3 \times 2 + 1 \times 0 + 2 \times 3 + 3 \times 1 + 1 \times 3\] \[ \vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C} = 2 + 6 + 0 + 6 + 3 + 3\] \[ \vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C} = 20\]

Exercício 12

Considere o vetor $\vec{F} = (x, y, z)$ perpendicular ao vetor $\vec{G} = (2, 3, 1)$. Sabendo que $\vec{F} \cdot \vec{F} = 9$. Determine os componentes que definem o vetor $\vec{F}$.

Exercício 13

Calcule o Produto Escalar de $\vec{C} = \vec{A} - \vec{B}$ com ele mesmo.

Produto Vetorial

Imagine dois vetores, $\vec{A}$ e $\vec{B}$, como setas lançadas no espaço. Agora, imagine desenhar um paralelogramo com as magnitudes de $\vec{A}$ e $\vec{B}$ como lados. O Produto Vetorial de $A$ e $B$, representado por $\vec{A} \times \vec{B}$, é como uma seta disparada diretamente para fora desse paralelogramo, tão perfeitamente perpendicular quanto um mastro em um navio.

A magnitude, o comprimento dessa seta, é a área do paralelogramo formado por $\vec{A}$ e $\vec{B}$. É um número simples, mas importante. Descreve o quão longe a seta resultante da interação entre $\vec{A}$ e $\vec{B}$ se estende no espaço. O comprimento do vetor resultado do Produto Vetorial. O resultado do Produto Vetorial entre dois vetores é um vetor.

imagine que temos dois vetores, firme e diretos, apontando em suas direções particulares no espaço. Chamamos eles de $\vec{A}$ e $\vec{B}$. Esses dois, em uma dança matemática, se entrelaçam em um Produto Vetorial, formando um terceiro vetor, o $\vec{C}$, perpendicular a ambos $\vec{A}$ e $\vec{B}$. Mais que isso, perpendicular ao paralelogramo formado por $\vec{A}$ e $\vec{B}$. Ainda mais, perpendicular ao plano formado por $\vec{A}$ e $\vec{B}$. Esta é a característica mais marcante do Produto Vetorial.

Portanto, a dança do Produto Vetorial é peculiar e intrigante, os dançarinos não trocam de lugar como a dança tradicional e a sequência de seus passos importa, mesmo assim ela acolhe a velha regra da distributividade. Uma dança peculiar no palco da matemática. Que leva a criação de uma novo dançarino, um novo vetor, perpendicular ao plano onde dançam os vetores originais. Esse novo vetor, esse Produto Vetorial, pode ser definido por uma equação analítica, geométrica, trigonométrica:

\[A \times B = \vert A \vert \vert B \vert sen(\theta_{AB}) a_n\]

Onde $a_n$ representa o vetor unitário na direção perpendicular ao plano formado pelo paralelogramo formado por $A$ e $B$. É uma fórmula simples, mas poderosa. Ela nos diz como calcular o Produto Vetorial, como determinar a direção, o sentido e a intensidade desta seta, lançada ao espaço.

A direção dessa seta, representada pelo vetor unitário $a_n$, será decidida pela regra da mão direita. Estenda a mão, seus dedos apontando na direção de $A$. Agora, dobre seus dedos na direção de $B$. Seu polegar, erguido, aponta na direção de $a_n$, na direção do Produto Vetorial.

O Produto Vetorial determina uma forma de conectar dois vetores, $A$ e $B$, e criar algo novo: um terceiro vetor, lançado diretamente para fora do plano criado por $A$ e $B$. E esse vetor, esse Produto Vetorial, tem tanto uma magnitude - a área do paralelogramo - quanto uma direção - decidida pela regra da mão direita. É uma forma de entender o espaço tridimensional. E como todas as coisas na álgebra vetorial, é simples, mas poderoso.

\[\vec{A} \times \vec{A} = \vert \vec{A} \vert \vert \vec{B} \vert sen(\theta_{AB}) a_n\]

É uma equação poderosa e simples, útil, muito útil, mas geométrica, trigonométrica e analítica. Algebricamente o Produto Vetorial pode ser encontrado usando uma matriz. As matrizes são os sargentos do exército da Álgebra Vetorial, úteis mas trabalhosas e cheias de regras. Considerando os vetores $\vec{a}=\, \vec{a}_x \, \vec{a}_x+\, \vec{a}_y \, \vec{a}_y+\, \vec{a}_z \, \vec{a}_z$ e $\vec{B}=B_x \, \vec{a}_x+B_y \, \vec{a}_y+B_z \, \vec{a}_z$ o Produto Vetorial $\vec{A}\times \vec{B}$ será encontrado resolvendo a matriz:

\[\vec{A}\times \vec{B}=\begin{vmatrix} \vec{a}_x & \, \vec{a}_y & \, \vec{a}_z\\ \vec{a}_x & \, \vec{a}_y & \, \vec{a}_z\\ B_x & B_y & B_z \end{vmatrix}\]

A matriz será sempre montada desta forma. A primeira linha om os vetores unitários, a segunda com o primeiro operando, neste caso os componentes de $\vec{A}$ e na terceira com os componentes de $\vec{B}$. A Solução deste produto será encontrada, mais facilmente com o Método dos Cofatores. Para isso vamos ignorar a primeira linha.

Ignorando também a primeira coluna, a coluna do vetor unitário $\vec{a}_x$ resta uma matriz composta de:

\[\begin{vmatrix} \vec{a}_y & \, \vec{a}_z\\ B_y & B_z \end{vmatrix}\]

O Esta matriz multiplicará o vetor unitário $\vec{a}_x$. Depois vamos construir outras duas matrizes como esta. A segunda será encontrada quando ignorarmos a coluna referente ao unitário $\vec{a}_y$, que multiplicará o oposto do vetor $\vec{a}_y$.

\[\begin{vmatrix} \vec{a}_x & \, \vec{a}_z\\ B_x & B_z \end{vmatrix}\]

Finalmente ignoramos a coluna referente ao vetor unitário $\vec{a}_z$ para obter:

\[\begin{vmatrix} \vec{a}_x & \, \vec{a}_y\\ B_x & B_y \end{vmatrix}\]

Que será multiplicada por $\, \vec{a}_z$. Colocando tudo junto, em uma equação matricial teremos:

\[\vec{A}\times \vec{B}=\begin{vmatrix} \vec{a}_x & \, \vec{a}_y & \, \vec{a}_z\\ \vec{a}_x & \, \vec{a}_y & \, \vec{a}_z\\ B_x & B_y & B_z \end{vmatrix}=\begin{vmatrix} \vec{a}_y & \, \vec{a}_z\\ B_y & B_z \end{vmatrix}\, \vec{a}_x-\begin{vmatrix} \vec{a}_x & \, \vec{a}_z\\ B_x & B_z \end{vmatrix}\, \vec{a}_y+\begin{vmatrix} \vec{a}_x & \, \vec{a}_y\\ B_x & B_y \end{vmatrix}\, \vec{a}_z\]

Cuide o negativo no segundo termo como cuidaria do leme do seu barco, sua jornada depende disso e o resultado do Produto Vetorial Também. Uma vez que a equação matricial está montada. Cada matriz pode ser resolvida usando a Regra de Sarrus que, para matrizes de $2\times 2$ se resume a uma multiplicação cruzada. Assim, nosso Produto Vetorial será simplificado por:

\[\vec{A}\times \vec{B}=(\vec{a}_y B_z- \, \vec{a}_z B_y)\, \vec{a}_x-(\vec{a}_x B_z-\, \vec{a}_z B_x)\,\vec{a}_y+(\vec{a}_x B_y-\, \vec{a}_y B_x)\, \vec{a}_z\]

Cuidado com os determinantes, o Chapeleiro não era louco por causa do chumbo, muito usado na fabricação de chapéus quando Lewis Carroll escreveu as histórias de Alice. Ficou louco resolvendo determinantes. Talvez um exemplo afaste a insanidade tempo suficiente para você continuar estudando eletromagnetismo.

Exemplo 12:
Dados os vetores $\vec{A}=\, \vec{a}_x+2\, \vec{a}_y+3\, \vec{a}_z$ e $\vec{B}=4\, \vec{a}_x+5\, \vec{a}_y-6\, \vec{a}_z$. (a) Calcule o Produto Vetorial entre $\vec{A}$ e $\vec{B}$. (b) Encontre o ângulo $\theta$ entre $\vec{A}$ e $\vec{B}$.

Solução:
(a) Vamos começar com o Produto Vetorial: \[ \vec{A}\times \vec{B}=\begin{vmatrix} \vec{a}_x & \, \vec{a}_y & \, \vec{a}_z\\ \vec{a}_x & \, \vec{a}_y & \, \vec{a}_z\\ B_x & B_y & B_z \end{vmatrix} = \begin{vmatrix} \vec{a}_x & \, \vec{a}_y & \, \vec{a}_z\\ 1 & 2 & 3\\ 4 & 5 & -6 \end{vmatrix} \] Que será reduzida a: \[ \vec{A}\times \vec{B} = \begin{vmatrix} 2 & 3\\ 5 & -6 \end{vmatrix}\, \vec{a}_x - \begin{vmatrix} 1 & 3\\ 4 & -6 \end{vmatrix}\, \vec{a}_y + \begin{vmatrix} 1 & 2\\ 4 & 5 \end{vmatrix}\, \vec{a}_z \] Usando Sarrus em cada uma destas matrizes teremos: \[\vec{A} \times \vec{B} = (2(-6) - 3(5)) \, \vec{a}_x - (1(-6)-3(4)) \, \vec{a}_y + (1(5)-2(4)) \, \vec{a}_z\] \[\vec{A} \times \vec{B} = -27 \, \vec{a}_x + 18 \, \vec{a}_y - 3 \, \vec{a}_z\] Esta foi a parte difícil, agora precisamos dos módulos, magnitudes, dos vetores $\vec{A}$ e $\vec{B}$. \[ \vert \vec{A} \vert = \sqrt{1^2+2^2+3^2} = \sqrt{14} \approx 3.74165\] \[ \vert \vec{B} \vert = \sqrt{4^2+5^2+6^2} = \sqrt{77} \approx 8.77496\] Para calcular o ângulo vamos usar a equação analítica, ou trigonométrica, do Produto Vetorial: \[\vec{A} \times \vec{B} = \vert \vec{A} \vert \vert \vec{B} \vert sen(\theta_{AB}) a_n\] A forma mais fácil de resolver este problema é aplicar o módulo aos dois lados da equação. Se fizermos isso, teremos: \[ \vert \vec{A} \times \vec{B} \vert = \vert \vec{A} \vert \vert \vec{B} \vert sen(\theta_{AB}) \vert a_n \vert \] Como $a_n$ é um vetor unitário, por definição $ \vert a_n \vert = 1$ logo: \[ \vert \vec{A} \times \vec{B} \vert = \vert \vec{A} \vert \vert \vec{B} \vert sen(\theta_{AB})\] Ou, para ficar mais claro: \[sen(\theta_{AB}) = \frac{ \vert \, \vec{a} \times \vec{B} \vert }{ \vert \, \vec{a} \vert \vert \vec{B} \vert }\] Os módulos de $\vec{A}$ e $\vec{B}$ já tenos, precisamos apenas do módulo de $\vec{A}\times \vec{B}$. \[ \vert \vec{A}\times \vec{B} \vert = \sqrt{27^2+16^2+3^2} = \sqrt{994} \approx 31.5298 \] Assim o seno do ângulo $\theta_{AB}$ será dado por: \[sen(\theta_{AB}) = \frac{\sqrt{994}}{(\sqrt{14})(\sqrt{77})} \approx \frac{31.5298}{(3.74165)(8.77496)}\] \[sen(\theta_{AB}) = 0.960316\] \[ \theta_{AB} =73.8^\circ \]

O Produto Vetorial é como uma dança entre vetores. E como todas as danças tem características únicas e interessantes expressas na forma de propriedades matemáticas:

1. Comutatividade: no universo dos vetores, há uma dança estranha acontecendo. $\vec{A} \times \vec{B}$ e $\vec{B} \times \vec{A}$ não são a mesma coisa, eles não trocam de lugar facilmente como dançarinos em um salão de baile. Em vez disso, eles são como dois boxeadores em um ringue, um o espelho do outro, mas em direções opostas. Assim, $\vec{A} \times \vec{B}$ é o oposto de $\vec{B} \times \vec{A}$. Assim, O Produto Vetorial não é comutativo:

   \[\vec{A} \times \vec{B} =-\vec{B} \times \vec{A}\]

2. Associatividade: imagine três dançarinos: $\vec{A}$, $\vec{B}$ e $\vec{C}$. A sequência de seus passos importa. $\vec{A}$ dançando com $\vec{B}$, depois com $\vec{C}$, não é o mesmo que $\vec{A}$ dançando com o resultado de $\vec{B}$ e $\vec{C}$ juntos. Assim como na dança, a ordem dos parceiros importa. O Produto Vetorial não é associativo. Desta forma:

   \[\vec{A} \times (\vec{B} \times \vec{C}) \neq (\vec{A} \times \vec{B}) \times \vec{C}\]

3. Distributividade: existe um aspecto familiar. Quando $\vec{A}$ dança com a soma de $\vec{B}$ e $\vec{C}$, é a mesma coisa que $\vec{A}$ dançando com $\vec{B}$ e depois com $\vec{C}$. O Produto Vetorial é distributivo. A distributividade, uma velha amiga, nos conhecemos deste dos tempos da aritmética, aparece aqui, guiando a dança. O que pode ser escrito como:

   \[\vec{A} \times (\vec{B}+\vec{C}) = \vec{A} \times \vec{B} + \vec{A} \times \vec{C}\]

4. Multiplicação por Escalar: agora entra em cena um escalar, $k$, um número simples, porém carregado de influência. Ele se aproxima do Produto Vetorial e o muda, mas não de forma selvagem ou imprevisível, e sim com a precisão de um relojoeiro. A magnitude do Produto Vetorial é esticada ou contraída pelo escalar, dependendo de seu valor. Isto pode ser escrito matematicamente como:

   \[k(A \times B) = (kA) \times B = A \times (kB)\]

   Porém, como o norte em uma bússola, a direção do Produto Vetorial não se altera. O resultado é um novo vetor, $\vec{D}$, que é um múltiplo escalar do original $\vec{C}$. O vetor $\vec{D}$ carrega a influência do escalar $k$, mas mantém a orientação e sentido originais de $\vec{C}$ para todo $k >0$.

5. Componentes Unitários: por fim, precisamos tirar para dançar os vetores unitários. Estrutura de formação dos nossos sistemas de coordenadas. Como Produto Vetorial $\vec{A}\times \vec{B}$ produz um vetor ortogonal ao plano formado por $\vec{A}$ e $\vec{B}$ a aplicação desta operação a dois dos vetores unitários de um sistema de coordenadas irá produzir o terceiro vetor deste sistema. Observando o Sistema de Coordenadas Cartesianas teremos:

\[\vec{a}_x\times \, \vec{a}_y = \, \vec{a}_z\] \[\vec{a}_x\times \, \vec{a}_z = \, \vec{a}_y\] \[\vec{a}_y\times \, \vec{a}_z = \, \vec{a}_x\]

Esta propriedade do Produto Vetorial aplicado aos componentes de um vetor é mais uma ferramenta que precisamos manter à mão. Um conjunto de regras que irão simplificar equações e iluminar o desconhecido de forma quase natural.

Exercício 14

Considerando a equação analítica do Produto escalar, $\vec{A} \cdot \vec{B} = \vert \vec{A} \vert \vert \vec{B} \vert cos(\theta)$, e a equação analítica do Produto Vetorial, $\vec{A} \times \vec{A} = \vert \vec{A} \vert \vert \vec{B} \vert sen(\theta_{AB})$ prove que estas duas operações são distributivas.

Produto Triplo Escalar

O Produto Triplo Escalar é um conceito matemático definido para operação de três vetores $\vec{A}$, $\vec{B}$, e $\vec{C}$ em um espaço tridimensional e será determinado por:

\[\vec{A} \cdot (\vec{B} \times \vec{C})\]

A equação tem suas raízes nas obras de matemáticos como Augustin-Louis Cauchy e Josiah Willard Gibbs, que contribuíram para o desenvolvimento da álgebra vetorial. A notação de Gibbs é particularmente útil para representar produtos escalares e vetoriais, bem como outras operações vetoriais. Segundo a notação de Gibbs, vetores são presentados por letras latinas em negrito $\mathbf{A}$ ou por letras com setas $\vec{A}$. Além disso, as notações que usamos para representar os produtos escalares e vetoriais, também foram desenvolvidas por Gibbs. Também devemos a Gibbs as representações das operações gradiente $\nabla$, o divergente, $\nabla \cdot \vec{F}$ e o rotacional, $\nabla \times \vec{F}$ do cálculo infinitesimal de campos vetoriais. Já Cauchy estudou a Álgebra Vetorial. Sua pesquisa com determinantes ajudou a definir o uso de determinantes para a solução de operações vetoriais.

O Produto Triplo Escalar pode ser expresso em termos de determinantes de matrizes. Se você tem três vetores $\vec{A} = [a_x, a_y, a_z]$, $\vec{B} = [b_x, b_y, b_z]$, e $\vec{C} = [c_x, c_y, c_z] ), o Produto Triplo Escalar $\vec{A} \cdot (\vec{B} \times \vec{C})$ será igual ao determinante da matriz $3x3$ formada pelos componentes desses vetores e dada por:

\[\vec{A} \cdot (\vec{B} \times \vec{C}) = \begin{vmatrix} a_x & a_y & a_z \\ b_x & b_y & b_z \\ c_x & c_y & c_z \end{vmatrix}\]

Cuja solução pode ser encontrada com as mesmas técnicas que usamos para resolver o Produto Vetorial. O Produto Triplo Escalar é uma extensão natural do produto vetorial e do produto escalar, e é uma ferramenta útil em várias áreas da ciência e da engenharia, incluindo física, eletromagnetismo, engenharia mecânica, e ciência da computação. A Leitora é de concordar que é uma operação simples. E como tudo que é simples, merece atenção.

O vetor $\vec{B} \times \vec{C}$ representa a área de um paralelogramo cujos lados serão dados por $\vec{B}$ e $\vec{C}$. Logo, $\vec{A} \cdot (\vec{B} \times \vec{C})$ representa essa área multiplicada pelo componente de $\vec{A}$ perpendicular a esta área o que resulta em um volume. Neste caso, o volume é o mesmo, não importa como você combine os vetores $\vec{A}$, $\vec{B}$, e $\vec{C $, no Produto Triplo Escalar com exceção de:

\[\vec{A} \cdot (\vec{B} \times \vec{C}) = -\vec{A} \cdot (\vec{C} \times \vec{B})\]

PRECISA REESCREVER PARA INCLUIR O CONCEITO DA REGRA DA MÃO DIREITA

Portanto, o valor do Produto Triplo Escalar $\vec{A} \cdot (\vec{B} \times \vecCA})$ é positivo se os vetores $\vec{A}$, $\vec{B}$, e $\vec{C}$ são organizados de tal forma que $\vec{A}$ está no mesmo lado do plano formado por $\vec{B}$ e $\vec{B}$ como indicado pela regra da mão direita ao rotacionar $\vec{B}$ para $\vec{C}$. O valor será negativo se $\vec{A}$ está no lado oposto deste plano. O produto triplo permanece inalterado se os operadores de produto escalar e vetorial forem trocados:

\[\vec{A} \cdot (\vec{B} \times \vec{C}) = \vec{A} \times (\vec{B} \cdot \vec{C})\]

O Produto Triplo Escalar também é invariante sob qualquer permutação cíclica de $\vec{A}$, $\vec{B}$, e $\vec{C}$,

\[\vec{A} \cdot (\vec{B} \times \vec{C}) = \vec{B} \cdot (\vec{C} \times \vec{A}) = \vec{C} \cdot (\vec{A} \times \vec{B})\]

Contudo qualquer permutação anti-cíclica faz com que o Produto Triplo Escalar mude de sinal,

\[\vec{A} \cdot (\vec{B} \times \vec{C}) = -\vec{B} \cdot (\vec{A} \times \vec{C})\]

O Produto Triplo Escalar é zero se quaisquer dois dos vetores $\vec{A}$, $\vec{B}$, e $\vec{C}$ são paralelos, ou se $\vec{A}$, $\vec{B}$, e $\vec{C}$ são coplanares. Se $\vec{A}$, $\vec{B}$, e $\vec{C}$ não são coplanares, então qualquer vetor $\vec{R}$ pode ser escrito em termos deles:

\[\vec{R} = \alpha \vec{A} + \beta \vec{B} + \gamma \vec{C}\]

Formando o produto escalar desta equação com $\vec{B} \times \vec{C}$, obtemos então

\[\vec{R} \cdot (\vec{B} \times \vec{C}) = \alpha \vec{A} \cdot (\vec{B} \times \vec{C})\]

portanto,

\[\alpha = \frac{\vec{R} \cdot (\vec{B} \times \vec{C})}{\vec{A} \cdot (\vec{B} \times \vec{C})}\]

Expressões análogas podem ser escritas para $\beta$ e $\gamma$. Os parâmetros $\alpha$, $\beta$, e $\gamma$ são unicamente determinados, desde que:

\[\vec{A} \cdot (\vec{B} \times \vec{C}) \neq 0\]

ou seja, desde que os três vetores base não sejam coplanares.

Usando a Álgebra Vetorial no Eletromagnetismo

Em um mundo onde a ciência se entrelaça com a arte, a álgebra vetorial se ergue como uma ponte sólida entre o visível e o invisível. Neste ponto da nossa jornada, navegaremos pelas correntes do eletromagnetismo, uma jornada onde cada vetor conta uma história, cada Produto Escalar revela uma conexão profunda, e cada Produto Vetorial desvenda um mistério. A matemática da Álgebra Vetorial é a ferramenta que nos guiará.

Prepare-se para uma surpresa olhe com cuidado e verá como a matemática se torna poesia, desvendando os segredos do universo elétrico e magnético. Esta rota promete uma jornada de descoberta, compreensão e surpresa. Começaremos pelo mais básico de todos os básicos, a Lei de Coulomb.

Lei de Coulomb

No ano da glória de 1785, um pesquisador francês, Charles-Augustin de CoulombFormulou, empiricamente uma lei para definir a intensidade da força exercida por uma carga elétrica $Q$ sobre outra dada por:

\[F_{21} = K_e \frac{Q_1Q_2}{R^2}\]

Charles-Augustin de Coulomb estabeleceu sua lei de forma empírica utilizando uma balança de torção para medir as forças de interação entre cargas elétricas estacionárias. Utilizando este método, ele foi capaz de quantificar a relação inversa entre a força e o quadrado da distância entre as cargas. De forma independente, Henry Cavendish chegou à mesma equação anos depois, também utilizando uma balança de torção, embora seus resultados não tenham sido amplamente publicados na época.

Até o surgimento do trabalho de Michael Faraday sobre linhas de força elétrica, a equação desenvolvida por Coulomb era considerada suficiente para descrever interações eletrostáticas. Quase um século depois de Coulomb, matemáticos como Gauss, Hamilton, Maxwell reformularam esta lei, incorporando-a em um contexto vetorial. Eles utilizaram o cálculo vetorial para expressar as direções e magnitudes da força, permitindo que Lei de Coulomb possa ser aplicada de forma mais geral em campos eletrostáticos e magnetostáticos.

\[F_{21} = \frac{1}{4\pi \epsilon_0 \epsilon_r} \frac{Q_1Q_2}{R^2} a_{21}\]

Nesta equação:

• $F_{21}$ é a força que é aplicada sobre a carga 2, $Q_2$, devido a existência da carga 1, $Q_1$.
• $\epsilon_0$ representa a permissividade do vácuo, medida em Farads por metro ($F/m$).
• $\epsilon_r$ representa a permissividade do meio onde as cargas estão, um valor escalar e sem unidade.
• $4\pi $ surge da existência da força em todos os pontos do espaço, uma esfera que se estende da carga até o infinito.
• $Q_1Q_2$ representa o produto entre as intensidades das cargas que no Sistema Internacional de Unidades são medidas em Coulombs ($C$).
• $a_{21}$ representa o vetor unitário com origem em $Q1$ e destino em $Q2$.

Cálculo Vetorial

Cálculo vetorial, soa como algo saído de uma história de ficção científica. Mas é mais terra-a-terra do que podemos imaginar de longe. Trata-se uma técnica para lidar com quantidades que têm tanto magnitude quanto direção de forma contínua. Velocidade. Força. Fluxo de um rio, Campos Elétricos, Campos Magnéticos. Coisas que não apenas têm um tamanho, mas também uma direção, um sentido. Não sei se já falei sobre isso, são as grandezas que chamamos de vetoriais e representamos por vetores.

A beleza do cálculo vetorial perceptível na sua capacidade de descrever o mundo físico profunda e significativamente.

Considere um campo de trigo balançando ao vento. O vento não está apenas soprando com uma certa força, mas também em uma certa direção. O cálculo vetorial nos permitirá entender fenômenos como esse e transformá-los em ferramentas de inovação e sucesso.

O cálculo vetorial é construído sobre três operações fundamentais: o gradiente, a divergência e o rotacional. O gradiente nos diz a direção e a taxa na qual uma quantidade está mudando. A divergência nos diz o quanto um campo está se espalhando de um ponto. E o rotacional nos dá uma medida da rotação ou vorticidade de um campo.

Se tivermos uma função escalar $\mathbf{F}$, o gradiente de $\mathbf{F}$ será dado por:

\[\nabla \mathbf{F} = \left( \frac{\partial \mathbf{F}}{\partial x}, \frac{\partial \mathbf{F}}{\partial y}, \frac{\partial \mathbf{F}}{\partial z} \right)\]

Se tivermos um campo vetorial $ \mathbf{F} = F_x \, \vec{a}_x + F_y \, \vec{a}_y + F_z \, \vec{a}_x $, a divergência de $\mathbf{F}$ é dada por:

\[\nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}\]

O rotacional de $\mathbf{F}$ será dado por:

\[\nabla \times \mathbf{F} = \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \right) \, \vec{a}_x - \left( \frac{\partial F_z}{\partial x} - \frac{\partial F_x}{\partial z} \right) a_i + \left( \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right) \, \vec{a}_z\]

A única coisa que pode encher seus olhos de lágrimas é o sal trazido pela maresia, não o medo do Cálculo Vetorial. Então, não se intimide por estas equações herméticas, quase esotéricas. O Cálculo Vetorial é apenas conjunto de ferramentas, como um canivete suíço, que nos ajuda a explorar e entender o mundo ao nosso redor. Nós vamos abrir cada ferramenta deste canivete e aprender a usá-las.

Campos Vetoriais

Quando olhamos as grandezas escalares, traçamos Campos Escalares. Como uma planície aberta, eles se estendem no espaço, sem direção, mas com magnitude, definidos por uma função $\mathbf{F}(x,y,z)$, onde $x$, $y$, $z$ pertencem a um universo de triplas de números reais. Agora, para as grandezas vetoriais, moldamos Campos Vetoriais, definidos por funções vetoriais $\mathbf{F}(x,y,z)$, onde $x$, $y$, $z$ são componentes vetoriais. Em outras palavras, representamos Campos Vetoriais no espaço como um sistema onde cada ponto do espaço puxa um vetor.

Imagine-se em um rio, a correnteza o arrastando, conduzindo seu corpo. A correnteza aplica uma força sobre seu corpo. O rio tem uma velocidade, uma direção. Em cada ponto, ele te empurra de uma forma diferente. Isso é um campo vetorial. Ele é como um mapa, com forças distribuídas, representadas por setas desenhadas para te orientar. Mas essas setas não são meras orientações. Elas têm um comprimento, uma magnitude, e uma direção e um sentido. Elas são vetores. E o mapa completo, deste rio com todas as suas setas, descreverá um campo vetorial.

Em cada ponto no espaço, o campo vetorial tem um vetor. Os vetores podem variar de ponto para ponto. Pense de novo no rio. Em alguns lugares, a correnteza é forte e rápida. Em outros, é lenta e suave. Cada vetor representará essa correnteza em um ponto específico. E o campo vetorial representará o rio todo.

Frequentemente, Campos Vetoriais são chamados para representar cenas do mundo físico: a ação das forças na mecânica, o desempenho dos campos elétricos e magnéticos no Eletromagnetismo, o fluxo de fluidos na dinâmica dos fluidos. Em cada ponto, as coordenadas $(x, y, z)$ são protagonistas, ao lado das funções escalares $P$, $Q$ e $R$. O vetor resultante no palco tem componentes nas direções $x$, $y$ e $z$, representadas pelos atores coadjuvantes, os vetores unitários $(\, \vec{a}_x, \, \vec{a}_y, \, \vec{a}_z)$.

Imaginar um campo vetorial no palco do espaço tridimensional é tarefa árdua que requer visão espacial, coisa para poucos. Para aqueles que já trilharam os caminhos árduos da geometria e do desenho tridimensional Se nosso palco for bidimensional, poderemos colocar os vetores em um plano, selecionar alguns pontos e traçar estes vetores. Neste caso voltaremos nossa atenção e esforço para trabalhar com apenas os componentes $x$ e $y$ e o campo vetorial será definido por uma função dada por:

\[\mathbf{F}(x, y) = (P(x, y), Q(x, y))\]

Uma função, uma definição direta, e simples, ainda assim, sem nenhum apelo visual. Mas somos insistentes e estamos estudando matemática, a rota que nos levará ao horizonte do Eletromagnetismo. Que nasce na carga elétrica, fenômeno simples, estrutural e belo que cria forças que se espalham por todo universo. Vamos pegar duas cargas de mesma intensidade e colocar no nosso palco.

Figura 3 - Diagrama de um campo vetorial em duas dimensões.

Agora podemos ver o Campo Vetorial, simples, com poucos pontos escolhidos no espaço e duas cargas pontuais representadas por círculos. Um vermelho, quente, para indicar a carga positiva outro azul, frio, para indicar a carga negativa. Treine a vista. Seja cuidadoso, detalhista. E verá a interação das forças em todos os pontos do espaço.

O Campo Elétrico, o Campo Vetorial que a figura apresenta, surge, na força da própria definição, na carga elétrica positiva por isso os vetores apontam para fora, para longe desta carga, divergem. E são drenados pela carga elétrica negativa, as setas apontam diretamente para ela, convergem. Em todos os pontos que escolhi para plotar em todo o espaço do plano desenhado, você pode ver o efeito das forças criadas por esta carga. Em alguns pontos um vetor está exatamente sobre o outro, eles se anulam, em todos os outros pontos do espaço se somam.

Visualizar um Campo Vetorial é como assistir a uma peça, com cada vetor como um ator em um gráfico. Cada vetor é um personagem desenhado com uma linha direcionada, geralmente com uma seta, atuando com direção e magnitude. Mas essa peça é complexa e exige tempo e paciência para ser compreendida. Uma abordagem mais simples seria tomar um ponto de teste no espaço e desenhar algumas linhas entre a origem do Campo Vetorial e esse ponto, traçando assim os principais pontos da trama.

O Campo Vetorial requer cuidado, carinho e atenção, ele está em todos os pontos do espaço. Contínuo e muitas vezes, infinito. Trabalhar com a continuidade e com o infinito requer mãos calejadas e fortes. Teremos que recorrer a Newton e Leibniz e ao Cálculo Integral e Diferencial. Não tema! Ainda que muitos se acovardem frente a continuidade este não será nosso destino. Vamos conquistar integrais e diferenciais como Odisseu conquistou Troia, antes de entrar em batalha vamos afiar espadas, lustrar escudos e lanças, na forma de gradiente, divergência e rotacional.

Gradiente

Imagine-se no topo de uma montanha, cercado por terreno acidentado. Seu objetivo é descer a montanha, mas o caminho não é claramente marcado. Você olha ao redor, tentando decidir para qual direção deve seguir. O gradiente é como uma bússola que indica a direção de maior inclinação. Se você seguir o gradiente, estará se movendo na direção de maior declividade. Se a velocidade for importante é nesta direção que descerá mais rápido.

Agora, vamos trazer um pouco de matemática para esta metáfora. Em um espaço de múltiplas dimensões. Imagine uma montanha com muitos picos e vales, e você pode se mover em qualquer direção, o gradiente de uma função em um determinado ponto é um vetor que aponta na direção de maior variação desta função. Se a função tem múltiplas dimensões, o gradiente é o vetor que resulta da aplicação das derivadas parciais da função.

Se tivermos uma função $\mathbf{F}(x, y)$, uma função escalar, o gradiente de $\mathbf{F}$ será dado por:

\[\nabla \mathbf{F} = \left( \frac{\partial \mathbf{F}}{\partial x}, \frac{\partial \mathbf{F}}{\partial y} \right)\]

Assim como a bússola na montanha, o gradiente nos mostra a direção à seguir para maximizar, ou minimizar, a função. É uma ferramenta importante na matemática e na física, especialmente em otimização e aprendizado de máquina. Mas não tire seus olhos do ponto mais importante: o gradiente é uma operação que aplicada a uma função escalar devolve um vetor. Em três dimensões, usando o Sistema de Coordenadas Cartesianas teremos:

\[\nabla \mathbf{F} = \left( \frac{\partial \mathbf{F}}{\partial x}, \frac{\partial \mathbf{F}}{\partial y}, \frac{\partial \mathbf{F}}{\partial z} \right)\]

onde $\frac{\partial \mathbf{F} }{\partial x}$, $\frac{\partial \mathbf{F}}{\partial y}$, e $\frac{\partial \mathbf{F}}{\partial z}$ são as derivadas parciais de $\mathbf{F}$ com respeito a $x$, $y$, e $z$ respectivamente.

Só a expressão Derivadas parciais pode fazer o coração bater mais rápido. O medo não o guiará aqui. As derivadas parciais são como velhos amigos que você ainda não conheceu.

Imagine-se em uma grande pradaria. O vento está soprando, carregando consigo o cheiro da grama e da terra. Você está livre para caminhar em qualquer direção. Para o norte, onde o sol se põe, ou para o sul, onde a floresta começa. Cada passo que você dá muda a paisagem ao seu redor, mas de formas diferentes dependendo da direção em que você escolheu caminhar.

A derivada parcial é apenas essa ideia, vestida com a roupa do cálculo. Ela apenas quer saber: e se eu der um pequeno passo para o norte, ou seja, mudar um pouco $x$, como a paisagem, nossa função, vai mudar? Ou o se for para o sul, ou em qualquer outra direção que escolher.

Então, em vez de temer as derivadas parciais, podemos vê-las como uma ferramentas úteis que nos ajudem a entender a terra sob nossos pés, o vento, a água que flui, o Campo Elétrico, entender a função que estamos usando para descrever o fenômeno que queremos entender. Com as derivadas parciais, podemos entender melhor o terreno onde pisamos, saber para onde estamos indo e como chegar lá. E isso é bom. Não é?

Uma derivada parcial de uma função de várias variáveis revela a taxa na qual a função muda quando pequenas alterações são feitas em apenas uma das incógnitas da função, mantendo todas as outras constantes. O conceito é semelhante ao conceito de derivada em cálculo de uma variável, entretanto agora estamos considerando funções com mais de uma incógnita.

Por exemplo, se temos uma função $\mathbf{F}(x, y)$, a derivada parcial de $\mathbf{F}$ em relação a $x$ (denotada por $\frac{\partial \mathbf{F}}{\partial x}$ mede a taxa de variação de $\mathbf{F}$ em relação a pequenas mudanças em $x$, mantendo $y$ constante. Da mesma forma, $\frac{\partial \mathbf{F}}{\partial y}$ mede a taxa de variação de $\mathbf{F}$ em relação a pequenas mudanças em $y$, mantendo $x$ constante. Em três dimensões, a derivada parcial em relação uma das dimensões é a derivada de $\mathbf{F}$ enquanto mantemos as outras constantes. Nada mais que a repetição, dimensão a dimensão da derivada em relação a uma dimensão enquanto as outras são constantes.

O gradiente mede a taxa em que o Campo Escalar varia em uma determinada direção. Para clarear e afastar a sombra das dúvidas, nada melhor que um exemplo.

Exemplo 13:
Considerando o Campo Escalar dado por $\mathbf{F}(x,y) = 10sin(\frac{x^2}{5})+4y$, (a) calcule a intensidade do campo no ponto $P(2,3)$, (b) o gradiente deste campo no ponto $P$.

Solução:
(a) A intensidade em um ponto é trivial, trata-se apenas da aplicação das coordenadas do ponto desejado na função do campo. Sendo assim: \[\mathbf{F}(x,y) = 10sin(\frac{x^2}{5})+4y\] \[\mathbf{F}(2,3) = 10sin(\frac{2^2}{5})\, \vec{a}_x+4(3)\, \vec{a}_y\] \[\mathbf{F}(2,3) = 7.17356\, \vec{a}_x+12\, \vec{a}_y\] (b) agora precisamos calcular o gradiente. O gradiente de uma função $\mathbf{F}(x, y)$ é um vetor que consiste nas derivadas parciais da função com respeito a cada uma de suas variáveis que representam suas coordenadas.

Vamos calcular as derivadas parciais de $\mathbf{F}$ com respeito a $x$ e $y$, passo a passo:

Primeiro, a derivada parcial de $f$ com respeito a $x$ é dada por: \[ \frac{\partial \mathbf{F}}{\partial x} = \frac{\partial}{\partial x} \left[10\sin\left(\frac{x^2}{5}\right) + 4y\right] \] Nós podemos dividir a expressão em duas partes e calcular a derivada de cada uma delas separadamente. A derivada de uma constante é zero, então a derivada de $4y$ com respeito a $x$ é zero. Agora, vamos calcular a derivada do primeiro termo: \[ \frac{\partial}{\partial x} \left[10\sin\left(\frac{x^2}{5}\right)\right] = 10\cos\left(\frac{x^2}{5}\right) \cdot \frac{\partial}{\partial x} \left[\frac{x^2}{5}\right] \] Usando a regra da cadeia, obtemos: \[ 10\cos\left(\frac{x^2}{5}\right) \cdot \frac{2x}{5} = \frac{20x}{5}\cos\left(\frac{x^2}{5}\right) = 4x\cos\left(\frac{x^2}{5}\right) \] Portanto, a derivada parcial de $\mathbf{F}$ com respeito a $x$ é: \[ \frac{\partial \mathbf{F}}{\partial x} = 4x\cos\left(\frac{x^2}{5}\right) \] Agora, vamos calcular a derivada parcial de $\mathbf{F}$ com respeito a $y$: \[ \frac{\partial \mathbf{F}}{\partial y} = \frac{\partial}{\partial y} \left[10\sin\left(\frac{x^2}{5}\right) + 4y\right] \] Novamente, dividindo a expressão em duas partes, a derivada do primeiro termo com respeito a $y$ é zero (pois não há $y$ no termo), e a derivada do segundo termo é $4$. Portanto, a derivada parcial de $\mathbf{F}$ com respeito a $y$ é: \[ \frac{\partial \mathbf{F}}{\partial y} = 4 \] Assim, o gradiente de $\mathbf{F}$ é dado por: \[ \nabla \mathbf{F} = \left[\frac{\partial \mathbf{F}}{\partial x}, \frac{\partial \mathbf{F}}{\partial y}\right] = \left(4x\cos\left(\frac{x^2}{5}\right), 4\right) \] E esta é a equação que define o gradiente. Para saber o valor do gradiente no ponto $P$ tudo que precisamos é aplicar o ponto na equação então: \[ \nabla \mathbf{F}(2,3) = \left( 4(2)\cos\left(\frac{2^2}{5}\right), 4\right) = \left( 5.57365, 4 \right) \] Ao derivarmos parcialmente o Campo Vetorial $\mathbf{F}$ escolhemos nosso Sistema de Coordenadas. Sendo assim: \[ \nabla \mathbf{F}(2,3) = 5.57365 \, \vec{a}_x+ 4\, \vec{a}_y \]

Assim como um navegador considera a variação da profundidade do oceano em diferentes direções para traçar a rota mais segura, a derivada parcial nos ajuda a entender como uma função se comporta quando mudamos suas variáveis de entrada. O gradiente é a forma de fazermos isso em todas as dimensões, derivando em uma incógnita de cada vez.

Significado do Gradiente

Em qualquer ponto $P$ o gradiente é um vetor que aponta na direção da maior variação de um Campo Escalar neste ponto. Nós podemos voltar ao exemplo 8 e tentar apresentar isso de uma forma mais didática. Primeiro o gráfico do Campo Escalar dado por: $\mathbf{F}(x,y) = 10sin(\frac{x^2}{5})+4y$.

Figura 4 - Gráfico de um Campo Escalar $f(x,y)$.

Na Figura 4 é possível ver a variação do do campo $\mathbf{F}(x,y)$ eu escolhi uma função em $\mathbf{F}(x,y)$ no domínio dos $\mathbb{R}^2$ por ser mais fácil de desenhar e visualizar, toda a variação fica no domínio de $z$. Podemos plotar o gradiente na superfície criada pelo campo $\mathbf{F}(x,y)$.

Figura 5 - Gráfico de um Campo Escalar $f(x,y) representando o Gradiente$.

Em cada ponto da Figura 5 a cor da superfície foi definida de acordo com a intensidade do gradiente. Quanto menor esta intensidade, mais próximo do vermelho. Quanto maior, mais próximo do Azul. Veja que a variação é maior nas bordas de descida ou subida e menor nos picos e vales. Coisas características da derivação.

É só isso. Se a paciente leitora entendeu até aqui, entendeu o gradiente e já sabe aplicá-lo. Eu disse que a pouparia de lágrimas desnecessárias. E assim o fiz.

Propriedades do Gradiente

O reino do gradiente é o reino dos Campos Escalares, o gradiente tem características matemáticas distintas que o guiam em sua exploração:

1. Linearidade: O gradiente é uma operação linear. Isso significa que para quaisquer campos escalares $f$ e $g$, e quaisquer constantes $a$ e $b$, temos:

   \[\nabla (af + bg) = a \nabla f + b \nabla g\]

   O gradiente de uma soma de funções é a soma dos gradientes das funções, cada um ponderado por sua respectiva constante.

2. Produto por Escalar: O gradiente de uma função escalar multiplicada por uma constante é a constante vezes o gradiente da função. Para uma função escalar $f$ e uma constante $a$, teremos:

   \[\nabla (af) = a \nabla f\]

3. Regra do Produto: Para o produto de duas funções escalares $f$ e $g$, a regra do produto para o gradiente é dada por:

   \[\nabla (fg) = f \nabla g + g \nabla f\]

   Esta é a versão para gradientes da regra do produto para derivadas no cálculo unidimensional.

4. Regra da Cadeia: Para a função composta $f(g(x))$, a regra da cadeia para o gradiente será dada por:

   \[\nabla f(g(x)) = (\nabla g(x)) f'(g(x))\]

   Esta é a extensão da regra da cadeia familiar do cálculo unidimensional.

Estas propriedades, como as leis imutáveis da física, regem a conduta do gradiente em sua jornada através dos campos escalares. No palco do eletromagnetismo, o gradiente desempenha um papel importante na descrição de como os Campos Elétrico e Magnético variam no espaço.

1. Campo Elétrico e Potencial Elétrico: o campo elétrico é o gradiente negativo do potencial elétrico. Isso significa que o Campo Elétrico aponta na direção de maior variação do potencial elétrico, formalmente expresso como:

   \[\mathbf{E} = -\nabla V\]

   Aqui, $\mathbf{E}$ é o Campo Elétrico e $V$ é o potencial elétrico. O gradiente, portanto, indica a encosta, o aclive, mais íngreme que uma partícula carregada experimentaria ao mover-se no Campo Elétrico.

2. Campo Magnético: o Campo Magnético não é o gradiente de nenhum potencial escalar, O Campo Magnético é um campo vetorial cuja divergência é zero. No entanto, em situações estáticas ou de baixas frequências, pode-se definir um potencial vetorial $\mathbf{A}$ tal que:

   \[\mathbf{B} = \nabla \times \mathbf{A}\]

Essas propriedades do gradiente são como setas, apontando o caminho através das complexidades do eletromagnetismo. O gradiente é a ferramenta mais simples do nosso canivete suíço do cálculo vetorial.

Divergência

Seu barco sempre será pequeno perto do oceano e da força do vento. Você sente o vento em seu rosto, cada sopro, uma força direcional, um vetor com magnitude e direção. Todo o oceano e a atmosfera acima dele compõem um campo vetorial, com o vento soprando em várias direções, forças aplicadas sobre o seu barco.

No oceano, o tempo é um caprichoso mestre de marionetes, manipulando o clima com uma rapidez alucinante. Agora, em uma tempestade, existem lugares onde o vento parece convergir, como se estivesse sendo sugado para dentro. Em outros lugares, parece que o vento está explodindo para fora. Esses são os pontos de divergência e convergência do campo vetorial do vento.

Um lugar onde o vento está sendo sugado para dentro tem uma divergência negativa - o vento está “fluido” para dentro mais do que está saindo. Um lugar onde o vento está explodindo para fora tem uma divergência positiva - o vento está saindo mais do que está entrando. Este é o conceito que aplicamos as cargas elétricas, o campo elétrico diverge das cargas positivas e converge para as negativas. Isto porque assim convencionamos há séculos, quando começamos e estudar o Eletromagnetismo.

Matematicamente, a divergência é uma forma de medir esses comportamentos de “expansão” ou “contração” de um campo vetorial. Para um campo vetorial em três dimensões, $\mathbf{F} = f_x \, \vec{a}_x + f_y \, \vec{a}_y + f_z \, \vec{a}_z$, a divergência é calculada como:

\[\nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}\]

A divergência, então, é como a “taxa de expansão” do vento em um determinado ponto - mostra se há mais vento saindo ou entrando em uma região específica do espaço, um lugar. assim como a sensação que temos no meio de uma tempestade. A divergência é o resultado do Produto Escalar entre o operador $\nabla$ e o Campo Vetorial. O resultado da divergência é uma função escalar que dá a taxa na qual o fluxo do campo vetorial está se expandindo ou contraindo em um determinado ponto.

Sendo um pouco mais frio podemos dizer que a divergência é um operador diferencial que atua sobre um Campo Vetorial para produzir um Campo Escalar. Em termos físicos, a divergência em um ponto específico de um Campo Vetorial representa a fonte ou dreno no ponto: uma divergência positiva indica que neste ponto existe uma fonte, ou fluxo de vetores para fora, divergindo. Enquanto uma divergência negativa indica um dreno ou fluxo para dentro, convergindo.

Fluxo e a Lei de Gauss

O fluxo, nas margens do cálculo vetorial, é uma medida da quantidade de campo que passa através de uma superfície. Imagine um rio, com a água fluindo com velocidades e direções variadas. Cada molécula de água tem uma velocidade - um vetor - e toda a massa de água compõe um Campo Vetorial.

Se você colocar uma rede no rio, o fluxo do campo de água através da rede seria uma medida de quanta água está passando por ela. Para um campo vetorial $\mathbf{F}$ e uma superfície $S$ com vetor normal dado por $\mathbf{n}$, o fluxo será definido, com a formalidade da matemática, como:

\[\iint_S (\mathbf{F} \cdot \mathbf{n}) \, dS\]

Uma integral dupla, integral de superfície onde $dS$ é o elemento diferencial de área da superfície, e o Produto Escalar $\mathbf{F} \cdot \mathbf{n}$ mede o quanto do campo está fluindo perpendicularmente à superfície.

Agora, a divergência entra em cena como a versão local do fluxo. Se encolhermos a rede até que ela seja infinitesimalmente pequena, o fluxo através da rede se tornará infinitesimal e será dado pela divergência do campo de água no ponto onde a rede está. Matematicamente, isso é expresso na Lei de Gauss:

\[\nabla \cdot \mathbf{F} = \frac{d (\text{Fluxo})}{dV}\]

Onde, $V$ é o volume da região, e a Lei de Gauss afirma que a divergência de um campo vetorial em um ponto é igual à taxa de variação do fluxo do campo através de uma superfície que envolve o ponto.

Teorema da Divergência

Imagine-se como um explorador atravessando o vasto terreno do cálculo vetorial. Você se depara com duas paisagens: a superfície e o volume. Cada uma tem suas próprias características e dificuldades, mas há uma ponte que as conecta, uma rota que permite viajar entre elas. Esta é a Lei de Gauss.

A Lei de Gauss, ou o Teorema da Divergência, é a ponte que interliga dois mundos diferentes. Ela afirma que, para um dado campo vetorial $\mathbf{F}$, a integral de volume da divergência do campo vetorial sobre um volume $V$ é igual à integral de superfície do campo vetorial através da superfície $S$ que delimita o volume $V$:

\[\iiint_V (\nabla \cdot \mathbf{F}) \, dV = \iint_S (\mathbf{F} \cdot \mathbf{n}) \, dS\]

Uma integral tripla igual a uma integral dupla. Aqui, $dV$ é um pedaço infinitesimalmente pequeno de volume dentro de $V$, e $dS$ é um pedaço infinitesimalmente pequeno da superfície $S$, respectivamente elemento infinitesimal de volume e área. O vetor $\mathbf{n}$ é um vetor normal apontando para fora da superfície.

Com a Lei de Gauss, podemos ir e voltar entre a superfície e o volume, entre o plano e o volume. Esta é a beleza e o poder da matemática: a linguagem e as ferramentas para navegar pelos mais complexos terrenos.

Propriedades da Divergência

No universo dos campos vetoriais, a divergência tem propriedades matemáticas distintas que servem como marcos na paisagem:

1. Linearidade: A divergência é uma operação linear. Isso significa que para quaisquer campos vetoriais $\mathbf{F}$ e $mathbf{G}$, e quaisquer escalares $a$ e $b$, temos:

   \[\nabla \cdot (a\mathbf{F} + b\mathbf{G}) = a (\nabla \cdot \mathbf{F}) + b (\nabla \cdot \mathbf{G})\]

   A divergência de uma soma é a soma das divergências, com cada divergência ponderada por seu respectivo escalar.

2. Produto por Escalar: A divergência de um campo vetorial multiplicado por um escalar é o escalar vezes a divergência do campo vetorial. Para um campo vetorial $\mathbf{F}$ e um escalar $a$, temos:

   \[\nabla \cdot (a\mathbf{F}) = a (\nabla \cdot \mathbf{F})\]

3. Divergência de um Produto: A divergência de um produto de um campo escalar $\phi$ e um campo vetorial $\mathbf{F}$ é dado por:

   \[\nabla \cdot (\phi \mathbf{F}) = \phi (\nabla \cdot \mathbf{F}) + \mathbf{F} \cdot (\nabla \phi)\]

Este é o análogo vetorial do produto de regra para derivadas no cálculo unidimensional.

1. Divergência do Rotação: A divergência do rotacional de qualquer campo vetorial é sempre zero:

   \[\nabla \cdot (\nabla \times \mathbf{F}) = 0\]

Esta propriedade é um reflexo do fato de que as linhas de campo do rotacional de um campo vetorial são sempre fechadas, sem início ou fim. Não se preocupe, ainda, já, já, chegaremos ao rotacional.

Essas propriedades são como as leis inabaláveis que governam o comportamento da divergência em sua jornada através dos campos vetoriais.

Rotacional

Imagine estar no meio de um tornado, onde o vento gira em um padrão circular em torno de um ponto central. O movimento deste vento pode ser descrito como um campo vetorial, que tem tanto uma direção quanto uma magnitude em cada ponto no espaço. Agora, considere um pequeno ponto neste campo - o rotacional é uma operação matemática que lhe dirá quão rapidamente e em que direção o vento está girando em torno deste ponto.

Para entender isso, vamos recorrer à matemática. O rotacional é um operador diferencial que atua sobre um campo vetorial, produzindo outro campo vetorial que descreve a rotação local do campo original. Se considerarmos um campo vetorial em três dimensões, representado por $\mathbf{F}(x, y, z)$, o rotacional desse campo será dado por:

\[\nabla \times \mathbf{F} = \left(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\right)\mathbf{i} + \left(\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}\right)\mathbf{j} + \left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\right)\mathbf{k}\]

Esta operação fornece uma descrição da rotação em cada ponto no espaço, sendo um vetor perpendicular ao plano de rotação, cuja magnitude representa a velocidade de rotação. Em outras palavras, o rotacional de um campo vetorial em um ponto particular indica quão giratório é o campo naquele ponto.

Imagine agora que você está no meio de um rio, onde a água gira em torno de algumas pedras, criando redemoinhos. O rotacional, nesse caso, poderia descrever como a água gira em torno desses pontos, permitindo-nos entender a dinâmica do fluxo de água neste rio.

É como uma dança, onde cada ponto no espaço executa uma rotação única, formando uma coreografia complexa e bela. Esta coreografia é o campo vetorial em questão. Entender o rotacional permite desvendar os segredos por trás dos padrões de fluxo em campos vetoriais, sejam eles campos de vento, campos magnéticos ou correntes de água.

No contexto do eletromagnetismo, o rotacional tem uma aplicação nas Equações de Maxwell. Uma das equações de Maxwell, especificamente a Lei de Ampère-Maxwell, é expressa como

\[\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}\]

onde $\nabla \times \mathbf{B}$ é o rotacional do campo magnético $\mathbf{B}$, $\mu_0$ é a permeabilidade do vácuo, $\mathbf{J}$ é a densidade de corrente elétrica e $\frac{\partial \mathbf{E}}{\partial t}$ é a variação do campo elétrico com relação ao tempo.

A Lei de Ampére-Maxwell representa a relação entre a corrente elétrica variável no tempo e o campo magnético rotativo que é gerado, sendo uma descrição matemática do fenômeno da indução eletromagnética. Desta forma, a operação do rotacional serve como uma ponte para unir e descrever fenômenos eletromagnéticos interdependentes, facilitando a análise e compreensão das interações complexas entre campos elétricos e magnéticos, essencial para a física moderna e inovações tecnológicas.

---