Parsers `LR(1)` - Fundamentos Teóricos e Aplicação Prática

Os Parsers LR(1) representam uma classe poderosa de analisadores sintáticos que utilizam uma abordagem bottom-up para analisar strings de entrada. Estes parsers são amplamente utilizados na implementação de compiladores e interpretadores devido à sua eficiência e capacidade de analisar uma ampla classe de gramáticas livres de contexto. Já discutimos anteriormente os parsers LL(1), que seguem uma abordagem top-down, e vimos como calcular os conjuntos $FIRST$ e $FOLLOW$ para estes parsers. Agora, vamos explorar a técnica LR(1), que utiliza uma abordagem completamente diferente para análise sintática.
Origens e Fundamentos dos Parsers LR
A notação LR(k) foi introduzida por Donald Knuth em 1965 e significa:
- L: Leitura da entrada da esquerda para a direita (Left-to-right);
- R: Derivação mais à direita em ordem reversa (Rightmost derivation in reverse);
- k: Número de símbolos de
lookaheadutilizados para tomar decisões (no caso doLR(1), apenas 1 símbolo).
Diferentemente dos parsers LL(1), que são top-down e constroem a árvore sintática a partir do símbolo inicial (raiz), os parsers LR(1) são bottom-up e constroem a árvore a partir das folhas (tokens) até a raiz. Esta abordagem permite que os parsers LR(1) lidem com uma classe maior de gramáticas, incluindo algumas com recursão à esquerda.
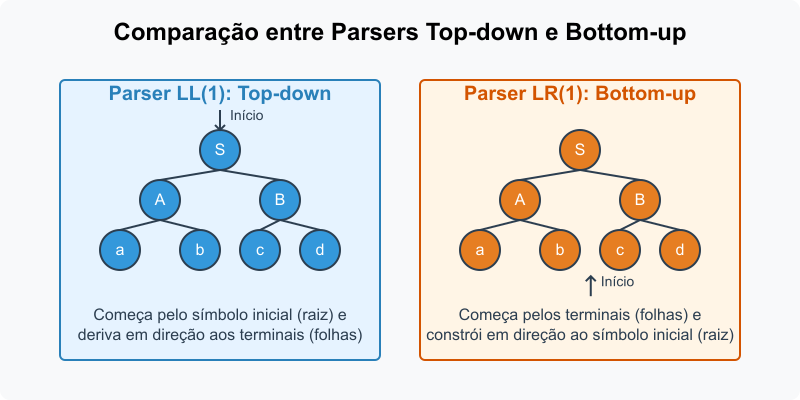
Figura 1: Comparação entre Parsers LL(1) e LR(1)
Na verdade, Em parsers LR(1), que são bottom-up, gramáticas com recursão à esquerda não são consideradas ruins. Na verdade, elas são frequentemente vistas como benéficas, especialmente em comparação com gramáticas recursivas à direita. Isso acontece porque a recursão à esquerda permite que o parser use menos espaço na pilha, pois reduz partes da entrada mais cedo, sem empilhar muitos símbolos. Além disso, a recursão à esquerda gera árvores de análise associadas também à esquerda, como em expressões como 1 - 2 - 3, interpretadas como (1 - 2) - 3, este é o comportamento esperado na maioria das linguagens. Finalmente, em muitos casos, a recursão à esquerda ajuda a evitar conflitos de análise, como os de shift-reduce, que podem ocorrer com gramáticas recursivas à direita. A Tabela 1 abaixo resume as diferenças entre recursão à esquerda e à direita:
| Aspecto | Recursão à Esquerda | Recursão à Direita |
|---|---|---|
| Uso de Memória (Stack) | Menor, reduz profundidade da pilha | Maior, pode crescer com o tamanho da entrada |
| Associatividade | À esquerda, comportamento esperado | À direita, menos comum em linguagens |
| Conflitos de Análise | Menos propensa em muitos casos | Pode causar shift-reduce em listas, por exemplo |
| Exemplo | E -> E + T | T (para expressões) |
Tabela 1: diferenças entre recurssão à esquerda e à direita nos parsers LR(1).
Componentes Fundamentais de um Parser LR(1)
Vamos criar um parser LR(1) utilizando os componentes fundamentais que o definem. Um parser LR(1) é composto por:
-
Pilha de Estados e Símbolos: armazena o histórico de símbolos lidos e estados visitados pelo parser. Tipicamente, alterna entre estados (números) e símbolos da gramática, terminais ou não-terminais. O topo da pilha sempre contém o estado atual;
-
Tabela de Parsing
LR(1): composta por duas sub-tabelas, geralmente pré-calculadas a partir da gramática:- ACTION: Indexada por
[estado, símbolo terminal (lookahead)], determina a ação a ser executada; - GOTO: Indexada por
[estado, símbolo não-terminal], determina o próximo estado após uma redução.
- ACTION: Indexada por
-
Buffer de Entrada: contém a sequência de tokens (terminais) a ser analisada, geralmente terminada com um marcador especial de fim de entrada (como
\$). Um ponteiro indica o próximo símbolo a ser lido (lookahead).
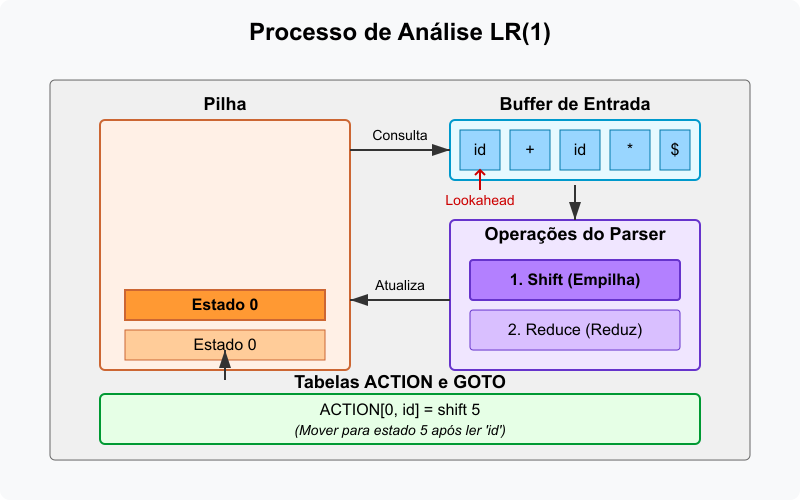
Figura 2: processo de análise de um parser LR(1).
Ações do Parser LR(1)
Com base no estado no topo da pilha e no símbolo de lookahead atual, o parser consulta a tabela ACTION e executa uma das quatro ações possíveis:
-
Shift (Empilhar): Se
ACTION[estado, lookahead] = shift j, o parser empilha o símbolo delookaheade, em seguida, empilha o novo estadoj. O ponteiro de entrada avança para o próximo símbolo. -
Reduce (Reduzir): Se
ACTION[estado, lookahead] = reduce k(na qual $k$ é o índice da produção $A \rightarrow \gamma$), o parser executa os seguintes passos:a. desempilha $2 \times |\gamma|$ itens da pilha, correspondentes aos símbolos de $\gamma$ e os estados intermediários; b. o estado $s’$ agora exposto no topo da pilha é o estado em que o parser estava antes de começar a reconhecer $\gamma$; c. consulta
GOTO[s', A] = j; d. empilha o símbolo não-terminal $A$ e, em seguida, empilha o novo estado $j$;A entrada não é consumida durante uma redução.
-
Accept (Aceitar): Se
ACTION[estado, lookahead] = accept, a análise terminou com sucesso. Isso geralmente ocorre quando o estado contém o item $[S’ \rightarrow S \cdot, \$]$ e o lookahead é\$. -
Error (Erro): Se
ACTION[estado, lookahead]está vazia (ou marcada como erro), um erro sintático foi detectado. O parser interrompe a análise e reporta o erro.
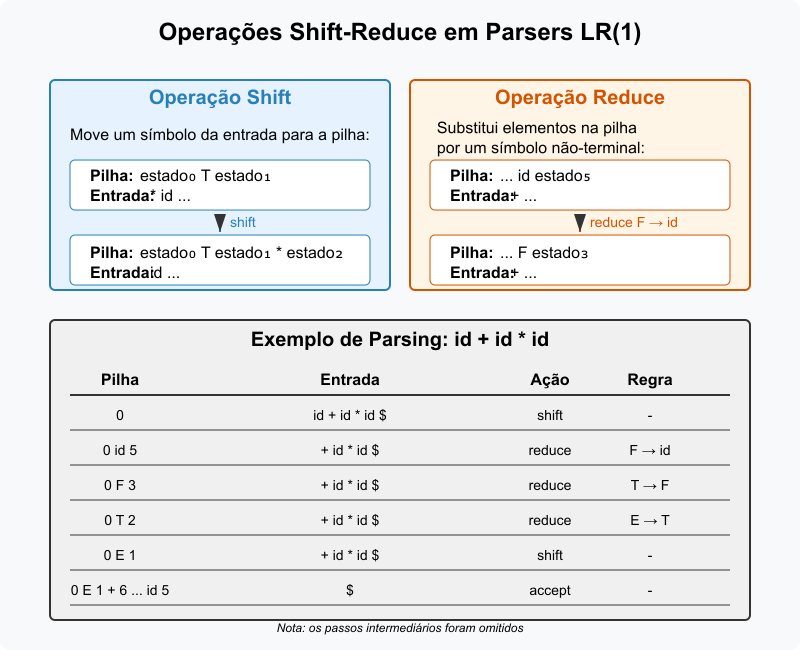
Figura 3: Exemplo de ações de shift e reduce em um parser LR(1).
Algoritmo de Análise LR(1) - Pseudocódigo
O fluxo geral do algoritmo que utiliza esses componentes e ações pode ser visualizado com o seguinte pseudocódigo:
# Assume que as tabelas ACTION e GOTO foram pré-calculadas
# Assume que 'producoes' é uma lista producoes[k] dá a regra k: (A, gamma)
# Assume que 'entrada_tokens' é a lista de terminais da entrada
def analisar_lr1(entrada_tokens, action_table, goto_table, producoes):
pilha = [0] # Começa com o estado inicial 0
entrada = entrada_tokens + ['$'] # Adiciona marcador de fim
ponteiro_entrada = 0
while True:
estado_topo = pilha[-1]
simbolo_atual = entrada[ponteiro_entrada]
if (estado_topo, simbolo_atual) not in action_table:
print(f"Erro de sintaxe: Nenhuma ação definida para estado {estado_topo} e símbolo '{simbolo_atual}'")
return False # Análise falhou
acao = action_table[(estado_topo, simbolo_atual)]
# Ação pode ser uma tupla ('s', novo_estado) ou ('r', num_producao) ou ('acc', 0)
tipo_acao = acao[0]
valor_acao = acao[1]
if tipo_acao == 's': # Shift
# Empilha o símbolo e o novo estado
pilha.append(simbolo_atual)
pilha.append(valor_acao)
# Avança na entrada
ponteiro_entrada += 1
# print(f"Shift: {simbolo_atual}, para estado {valor_acao}. Pilha: {pilha}") # Debug
elif tipo_acao == 'r': # Reduce
A, gamma = producoes[valor_acao] # Assume gamma é uma lista/tupla de símbolos
tamanho_gamma = len(gamma)
# Desempilha 2 * |gamma| itens (símbolo + estado para cada símbolo em gamma)
if tamanho_gamma > 0:
pilha = pilha[:- (2 * tamanho_gamma)]
estado_exposto = pilha[-1]
# Consulta GOTO
if (estado_exposto, A) not in goto_table:
print(f"Erro: GOTO não definido para estado {estado_exposto} e não-terminal '{A}'")
return False # Análise falhou
novo_estado = goto_table[(estado_exposto, A)]
# Empilha o não-terminal e o novo estado GOTO
pilha.append(A)
pilha.append(novo_estado)
# print(f"Reduce: {A} -> {' '.join(gamma)}. Ir para estado {novo_estado}. Pilha: {pilha}") # Debug
elif tipo_acao == 'acc': # Accept
print("Entrada aceita com sucesso!")
return True # Análise bem-sucedida
else:
# Considera qualquer outra coisa como erro implícito ou explícito na tabela
print(f"Erro de sintaxe ou ação desconhecida para estado {estado_topo} e símbolo '{simbolo_atual}'")
return False # Análise falhou
# Exemplo de como chamar (requer tabelas e produções definidas)
# sucesso = analisar_lr1(['id', '+', 'id', '$'], ACTION, GOTO, PRODUCOES)
Este pseudocódigo (em formato Python) ilustra a lógica central: um loop que continuamente consulta a tabela ACTION com base no estado atual (topo da pilha) e no lookahead, executando a ação correspondente (Shift, Reduce, Accept ou Error), manipulando a pilha e avançando na entrada (apenas no Shift) até a aceitação ou um erro.
Construção da Tabela de Parsing LR(1)
É importante notar uma diferença entre a análise usando um parser LR(1) e a construção do próprio parser. Embora a análise com uma tabela LR(1) já pronta seja muito eficiente, operando em tempo linear ($O(n)$) em relação ao tamanho $n$ da entrada, a construção da coleção canônica de itens LR(1) e, consequentemente, da tabela de parsing, pode ser computacionalmente cara. No pior caso, o número de estados LR(1) pode crescer exponencialmente em relação ao tamanho da gramática.
Essa potencial complexidade na construção é uma das principais motivações para o desenvolvimento e uso das variantes LALR(1) e SLR(1). Estes outros parsers geram tabelas de parsing significativamente menores, geralmente do mesmo tamanho que as SLR(1), tornando a geração do parser mais viável para gramáticas grandes, ao custo de um poder de reconhecimento ligeiramente menor em comparação com o LR(1) puro. Isso justifica ainda mais a dependência de ferramentas automatizadas como YACC/Bison, que implementam esses algoritmos de construção de forma otimizada.
A construção da tabela LR(1) é um processo complexo que envolve vários passos:
1. Gramática Aumentada
O primeiro passo é criar uma gramática aumentada adicionando uma nova produção $S’ \rightarrow S$, na qual, $S$ é o símbolo inicial original. Isso garante que haja apenas uma redução possível para o símbolo inicial.
2. Itens LR(1)
Um item LR(1) consiste em:
- uma produção com um marcador (ponto) indicando a posição atual na produção;
- um símbolo de
lookaheadque representa o terminal que pode seguir esta produção.
Por exemplo, para a produção $A \rightarrow \alpha\beta$, um item LR(1) poderia ser $[A \rightarrow \alpha \cdot \beta, a]$, onde o ponto indica que $\alpha$ já foi reconhecido e $\beta$ é esperado a seguir, com o terminal $a$ como lookahead.

Figura 4: Exemplo de itens LR(1) com o ponto indicando a posição atual na produção. Os símbolos de lookahead são mostrados à direita do ponto.{ : class=”legend”}
3. Conjuntos de Itens LR(1)
Os conjuntos de itens LR(1), também chamados de estados do parser, são criados através do fechamento (closure) e da operação de transição (goto). Estas operações são fundamentais para construir a Coleção Canônica de Estados, que por sua vez é usada para gerar as tabelas ACTION e GOTO.
Operação de Fechamento (Closure)
A operação $CLOSURE(I)$ calcula o conjunto completo de itens LR(1) que são implicitamente representados por um conjunto inicial de itens $I$. A ideia é que, se o parser está esperando ver um não-terminal $B$ após ter reconhecido uma sequência $\alpha$ (representado pelo item $[A \rightarrow \alpha \cdot B\beta, a]$), ele também precisa estar preparado para reconhecer qualquer sequência que possa iniciar uma derivação de $B$.
A regra formal é:
- Inicialmente, adicione todos os itens em $I$ para $CLOSURE(I)$
- Repetitivamente, para cada item da forma $[A \rightarrow \alpha \cdot B\beta, a]$ em $CLOSURE(I)$, na qual $B$ é um não-terminal, e para cada produção $B \rightarrow \gamma$ na gramática: Calcule $FIRST(\beta a)$. Para cada terminal $b$ neste conjunto $FIRST$, adicione o item $[B \rightarrow \cdot \gamma, b]$ a $CLOSURE(I)$, a menos que ele já esteja presente.
- Continue até que nenhum novo item possa ser adicionado a $CLOSURE(I)$.
Operação de Transição (GOTO)
A operação $GOTO(I, X)$ modela a transição do parser de um estado (conjunto de itens $I$) para outro estado ao reconhecer o símbolo gramatical $X$ (seja ele terminal ou não-terminal).
A regra formal é: se $I$ é um conjunto de itens e $X$ é um símbolo gramatical, então $GOTO(I, X)$ é o fechamento (closure) do conjunto de todos os itens $[A \rightarrow \alpha X \cdot \beta, a]$ tais que o item original $[A \rightarrow \alpha \cdot X\beta, a]$ está em $I$. Essencialmente, movemos o ponto . sobre o símbolo $X$ para todos os itens aplicáveis em $I$ e depois calculamos o closure desse novo conjunto.
4. Construção da Coleção Canônica de Estados
A coleção canônica $C$ de conjuntos de itens LR(1) para uma gramática aumentada $G’$ é a base para construir a tabela de parsing. O processo começa com o estado inicial $I_0$ e explora todas as transições possíveis usando GOTO.
- Estado Inicial: $I_0 = CLOSURE({[S’ \rightarrow \cdot S, $]})$, na qual $S’$ é o novo símbolo inicial da gramática aumentada e $$$ é o marcador de fim de entrada;
- Exploração: Para cada conjunto de itens $I_i$ em $C$ e cada símbolo gramatical $X$: Calcule $I_j = GOTO(I_i, X)$. Se $I_j$ não for vazio e ainda não estiver em $C$, adicione $I_j$ a $C$;
- Repita o passo 2 até que nenhum novo conjunto de itens possa ser adicionado a $C$.
Aplicando Closure ao Estado Inicial (I₀) para o Exemplo Prático
Vamos usar a gramática aumentada do exemplo:
\[\begin{array}{rcl} E' & \rightarrow & E \\ E & \rightarrow & E + T \mid T \\ T & \rightarrow & T * F \mid F \\ F & \rightarrow & (E) \mid id \end{array}\]E os conjuntos FIRST relevantes: $FIRST(() = {( }$, $FIRST(id) = {id }$, $FIRST(+) = {+}$, $FIRST() = {}$.
Calculamos $I_0 = CLOSURE({[E’ \rightarrow \cdot E, $]})$.
-
Início: $I_0 = { [E’ \rightarrow \cdot E, $] }$.
-
Processando $[E’ \rightarrow \cdot E, $]$:
- o ponto está antes do não-terminal $E$. Precisamos adicionar itens para as produções de $E$;
- o
lookaheadé determinado por $FIRST(\text{nada} $) = FIRST($) = {$}$; - adicionamos: $[E \rightarrow \cdot E + T, $]$ e $[E \rightarrow \cdot T, $]$;
- agora, $I_0 = { [E’ \rightarrow \cdot E, $], [E \rightarrow \cdot E + T, $], [E \rightarrow \cdot T, $] }$.
-
Processando $[E \rightarrow \cdot E + T, $]$:
- o ponto está antes de $E$. Adicionamos itens para $E$;
- o
lookaheadé $FIRST(+ T $) = FIRST(+) = {+}$; - adicionamos: $[E \rightarrow \cdot E + T, +]$ e $[E \rightarrow \cdot T, +]$;
- agora, $I_0$ contém os itens anteriores mais estes dois. (Note que os itens são únicos pela combinação produção+ponto+
lookahead).
-
Processando $[E \rightarrow \cdot T, $]$ e $[E \rightarrow \cdot T, +]$:
- o ponto está antes do não-terminal $T$. Precisamos adicionar itens para as produções de $T$;
- os
lookaheadssão derivados de $FIRST(\text{nada} $) = {$}$ e $FIRST(\text{nada} +) = {+}$. Conjunto delookaheads: ${$, +}$; - adicionamos: $[T \rightarrow \cdot T - F, $/+]$ e $[T \rightarrow \cdot F, $/+]$;
- $I_0$ agora contém os itens anteriores mais estes.
-
Processando $[T \rightarrow \cdot T - F, $/+]$:
- o ponto está antes de $T$. Adicionamos itens para $T$;
- o
lookaheadé $FIRST(- F ($/+)) = FIRST() = {}$; - adicionamos: $[T \rightarrow \cdot T - F, *]$ e $[T \rightarrow \cdot F, *]$;
- $I_0$ agora contém os itens anteriores mais estes.
-
Processando $[T \rightarrow \cdot F, $/+]$ e $[T \rightarrow \cdot F, *]$:
- o ponto está antes do não-terminal $F$. Precisamos adicionar itens para as produções de $F$;
- os lookaheads são derivados de $FIRST(\epsilon ($/+)) = {$, +}$ e $FIRST(\epsilon ) = {}$. Conjunto de
lookaheads: ${$, +, *}$; - adicionamos: $[F \rightarrow \cdot (E), $/+/ *]$ e $[F \rightarrow \cdot id, $/+/ *]$.
- $I_0$ agora contém os itens anteriores mais estes.
-
Processando $[F \rightarrow \cdot (E), $/+/ *]$ e $[F \rightarrow \cdot id, $/+/ *]$:
- O ponto está antes dos terminais
(eid. Nenhuma produção começa com terminal, então não adicionamos mais nada derivado destes.
- O ponto está antes dos terminais
-
Conclusão do Closure: Nenhum item novo pode ser adicionado. O conjunto final $I_0$ é:
I₀ = { [E' → • E, $], [E → • E + T, $/+], # Combina lookaheads $ e + [E → • T, $/+], # Combina lookaheads $ e + [T → • T * F, $ / + / *], # Combina lookaheads $, + e * [T → • F, $ / + / *], # Combina lookaheads $, + e * [F → • (E), $ / + / *], # Combina lookaheads $, + e * [F → • id, $ / + / *] # Combina lookaheads $, + e * }(Nota: Agrupamos os lookaheads para itens com a mesma produção e posição do ponto para clareza. O conjunto resultante corresponde ao Estado 0 (Inicial) apresentado na seção de exemplo prático).
A partir deste estado $I_0$, aplicaríamos a operação GOTO para cada símbolo ($E, T, F, (, id, +, *$) para encontrar os próximos estados da coleção canônica ($I_1, I_2$, etc.).
5. Construção das Tabelas ACTION e GOTO
As tabelas ACTION e GOTO são construídas a partir da coleção canônica de estados $C = {I_0, I_1, …, I_n}$:
-
ACTION[i, a]: Definida para o estado $I_i$ e o terminal $a$.
- Se $[A \rightarrow \alpha \cdot a\beta, b]$ está em $I_i$ e $GOTO(I_i, a) = I_j$, então $ACTION[i, a] = \text{shift } j$. (Priorizar Shift em caso de conflito S/R, a menos que regras de precedência digam o contrário);
- Se $[A \rightarrow \alpha \cdot, a]$ está em $I_i$ e $A \neq S’$, então $ACTION[i, a] = \text{reduce } A \rightarrow \alpha$;
- Se $[S’ \rightarrow S \cdot, $]$ está em $I_i$, então $ACTION[i, $] = \text{accept}$;
- Caso contrário, $ACTION[i, a] = \text{error}$ (entrada em branco na tabela).
-
GOTO[i, A]: Definida para o estado $I_i$ e o não-terminal $A$.
- Se $GOTO(I_i, A) = I_j$, então $GOTO[i, A] = j$;
- Caso contrário, $GOTO[i, A] = \text{error}$.
Conflitos em Parsers LR(1)
Mesmo com parsers LR(1), podem ocorrer conflitos na tabela de parsing:
- Conflito Shift-Reduce: Ocorre quando o parser não pode decidir se deve fazer um shift ou uma redução;
- Conflito Reduce-Reduce: Ocorre quando há mais de uma regra de redução possível para uma mesma combinação de estado e
lookahead.
Estes conflitos indicam ambiguidades na gramática ou limitações do parser LR(1).
Exemplo Prático
Vamos construir um parser LR(1) para uma gramática simples:
Gramática Aumentada
\[\begin{array}{rcl} E' & \rightarrow & E \\ E & \rightarrow & E + T \mid T \\ T & \rightarrow & T * F \mid F \\ F & \rightarrow & (E) \mid id \end{array}\]Conjuntos FIRST e FOLLOW
\[\begin{array}{rcl} FIRST(E) & = & \{(, id\} \\ FIRST(T) & = & \{(, id\} \\ FIRST(F) & = & \{(, id\} \\ \\ FOLLOW(E) & = & \{+, ), \$\} \\ FOLLOW(T) & = & \{+, *, ), \$\} \\ FOLLOW(F) & = & \{+, *, ), \$\} \\ \end{array}\]Coleção Canônica de Estados
A construção completa da coleção canônica de estados é extensa, mas podemos ilustrar os primeiros estados:
Estado 0 (Inicial):
[E' → • E, $]
[E → • E + T, +/$]
[E → • T, +/$]
[T → • T * F, +//$]
[T → • F, +//$]
[F → • (E), +//$]
[F → • id, +//$]
Estado 1 (após ler E):
[E' → E •, $]
[E → E • + T, +/$]
Estado 2 (após ler T):
[E → T •, +/$]
[T → T • * F, +/*/$]
E assim por diante…
Tabela ACTION e GOTO
A tabela ACTION e GOTO completa seria extensa, mas podemos ilustrar algumas entradas:
| ACTION | GOTO | ||||||
|---|---|---|---|---|---|---|---|
| Estado | id | + | * | $ | E | T | F |
| 0 | s5 | 1 | 2 | 3 | |||
| 1 | s6 | acc | |||||
| 2 | r2 | s7 | r2 | ||||
Na qual:
- s5: shift para o estado $5$;
- r2: reduce usando a produção $2$;
- acc: aceitar a entrada;
- $1$, $2$, $3$: próximo estado após a leitura de um não-terminal.
Exemplo de Análise
Vamos analisar a entrada id + id * id:
| Pilha | Entrada | Ação |
|---|---|---|
| 0 | id + id * id $ | shift 5 |
| 0 id 5 | + id * id $ | reduce F → id |
| 0 F 3 | + id * id $ | reduce T → F |
| 0 T 2 | + id * id $ | reduce E → T |
| 0 E 1 | + id * id $ | shift 6 |
| 0 E 1 + 6 | id * id $ | shift 5 |
| 0 E 1 + 6 id 5 | * id $ | reduce F → id |
| 0 E 1 + 6 F 3 | * id $ | reduce T → F |
| 0 E 1 + 6 T 9 | * id $ | shift 7 |
| 0 E 1 + 6 T 9 * 7 | id $ | shift 5 |
| 0 E 1 + 6 T 9 * 7 id 5 | $ | reduce F → id |
| 0 E 1 + 6 T 9 * 7 F 10 | $ | reduce T → T * F |
| 0 E 1 + 6 T 9 | $ | reduce E → E + T |
| 0 E 1 | $ | accept |
Vantagens dos Parsers LR(1)
Os parsers LR(1) possuem várias vantagens em relação a outros tipos de parsers:
- Maior Poder de Reconhecimento: Reconhecem mais gramáticas livres de contexto que parsers
LL(1), incluindo algumas com recursão à esquerda. - Detecção de Erros: Detectam erros sintáticos o mais cedo possível durante a análise.
- Eficiência: Operam em tempo linear $(O(n))$, na qual $n$ é o tamanho da entrada.
Implementação e Ferramentas
Na prática, a implementação manual de parsers LR(1) é raramente necessária, dada a complexidade da construção manual da tabela e da coleção canônica de estados. Felizmente, existem ferramentas poderosas que automatizam esse processo.
Conflitos e Resolução em Ferramentas
Durante a construção da tabela de parsing LR(1) (ou suas variantes como LALR(1), comumente usada por ferramentas), podem surgir conflitos, que indicam que a gramática pode ser ambígua ou inadequada para o método de parsing específico. Os principais tipos são:
-
Conflito Shift/Reduce: Ocorre em um estado $I_i$ quando, para um mesmo símbolo de
lookahead$a$, a tabela sugere duas ações possíveis:- Um item $[A \rightarrow \alpha \cdot a \beta, b]$ no estado $I_i$ sugere a ação
shift, empilhar $a$ e ir para o estado $GOTO(I_i, a)$. - Um item completo $[B \rightarrow \gamma \cdot, a]$ no mesmo estado $I_i$ sugere a ação
reduceusando a produção $B \rightarrow \gamma$.
O parser fica sem saber qual ação tomar. Um exemplo clássico que causa isso é a gramática do “dangling else”:
\[\begin{array}{rcl} Stmt & \rightarrow & \textbf{if } Expr \textbf{ then } Stmt \\ & \mid & \textbf{if } Expr \textbf{ then } Stmt \textbf{ else } Stmt \\ & \mid & other \end{array}\]Em algum estado, o parser pode ver um
elsecomolookaheade não saber se ele pertence aoifmais interno (shift) ou se deve reduzir oif then Stmtmais interno (reduce). - Um item $[A \rightarrow \alpha \cdot a \beta, b]$ no estado $I_i$ sugere a ação
-
Conflito Reduce/Reduce: Ocorre em um estado $I_i$ quando, para um mesmo símbolo de
lookahead$a$, existem dois ou mais itens completos diferentes que sugerem reduções distintas:- $[A \rightarrow \alpha \cdot, a]$ sugere reduzir por $A \rightarrow \alpha$.
- $[B \rightarrow \beta \cdot, a]$ sugere reduzir por $B \rightarrow \beta$. O parser não sabe qual redução aplicar. Este tipo de conflito geralmente indica um problema mais sério na gramática.
Ferramentas como YACC (Yet Another Compiler-Compiler), Bison, uma reimplementação do YACC, e ANTLR podem gerar automaticamente parsers, frequentemente LALR(1) ou outras variantes LR, a partir de uma especificação de gramática. Estas ferramentas detectam esses conflitos durante a geração do parser. Elas também fornecem mecanismos para resolvê-los, especialmente os conflitos shift/reduce, através de declarações de precedência e associatividade para os operadores.
Por exemplo, na nossa gramática de expressões, a ambiguidade entre id + id * id (poderia ser $(id + id) * id$ ou $id + (id * id)$) gera um conflito shift/reduce. O YACC/Bison resolve isso com diretivas como %left, %right ou %nonassoc.
Exemplo de Especificação YACC/Bison
Um exemplo de especificação para a nossa gramática de expressões em YACC/Bison, demonstrando a resolução de conflitos, seria:
%token ID // Declara o token para identificadores
// Define associatividade e precedência (menor para maior)
%left '+' // '+' é associativo à esquerda
%left '*' // '*' é associativo à esquerda e tem maior precedência que '+'
%% // Início das regras da gramática
expr : expr '+' term { /* ação semântica opcional */ }
| term
;
term : term '*' factor { /* ação semântica opcional */ }
| factor
;
factor : '(' expr ')' { /* ação semântica opcional */ }
| ID { /* ação semântica opcional */ }
;
%% // Seção opcional para código C adicional
Neste exemplo:
- A diretiva
%token IDdeclaraIDcomo um símbolo terminal que será fornecido pelo analisador léxico; - As diretivas
%left '+'e%left '*'declaram que ambos os operadores são associativos à esquerda. A ordem em que são declaradas define a precedência: como*é declarado depois de+,*tem precedência maior que+; - Quando o parser encontra um estado que apresenta um conflito do tipo shift/reduce envolvendo esses operadores (por exemplo, ao ver um
+ou*nolookaheadapós ter lido uma sequência que poderia ser reduzida por uma regra contendo+ou*`), ele utiliza essas declarações de precedência e associatividade para decidir a ação:- Se o
lookaheadé+e a regra que poderia ser reduzida envolve*(que tem maior precedência), o parser escolherá reduzir; - Se o
lookaheadé*(maior precedência) e a regra que poderia ser reduzida envolve+(menor precedência), o parser escolherá fazer shift (ler o*); - Se o
lookaheade o operador na regra têm a mesma precedência (por exemplo,lookahead+e regra envolvendo+), a associatividade%leftinstrui o parser a reduzir (implementando a associatividade à esquerda, ou seja, calculandoa + bantes de+ cema + b + c).
- Se o
Estas ferramentas, portanto, não só geram o código do parser de forma eficiente, mas também fornecem mecanismos declarativos essenciais para ajudar a refinar a gramática, resolver ambiguidades e garantir que a análise sintática corresponda à semântica desejada para a linguagem.
Os parsers LR(1) representam uma técnica poderosa para análise sintática, especialmente para linguagens de programação. Embora sua construção manual seja complexa, ferramentas automatizadas tornam sua utilização prática e eficiente. A compreensão dos princípios subjacentes aos parsers LR(1) é fundamental para qualquer estudo sério sobre compiladores e linguagens formais.
Referências
KNUTH, Donald E. On the Translation of Languages from Left to Right. Information and Control, v. 8, n. 6, p. 607-639, dezembro 1965. DOI: 10.1016/S0019-9958(65)90426-2.
AHO, Alfred V. et al. Compiladores: princípios, técnicas e ferramentas. 2. ed. São Paulo: Pearson Addison Wesley, 2008.
GRUNE, Dick; JACOBS, Ceriel J. H. Parsing Techniques: A Practical Guide. 2. ed. New York: Springer, 2008.
APPEL, Andrew W. Modern Compiler Implementation in Java. 2. ed. Cambridge: Cambridge University Press, 2002.
LEVINE, John R.; MASON, Tony; BROWN, Doug. Lex & Yacc. 2. ed. Sebastopol: O’Reilly Media, 1992.
HOPCROFT, John E.; MOTWANI, Rajeev; ULLMAN, Jeffrey D. Introdução à Teoria de Autômatos, Linguagens e Computação. 3. ed. São Paulo: Pearson Education do Brasil, 2011.
COOPER, Keith D.; TORCZON, Linda. Construindo Compiladores. Rio de Janeiro: Elsevier, 2014.
