Os desafios da norma IEEE 754

A memória é escassa, limitada, insuficiente e inteira. O arredondamento de números reais é inevitável, levantando um dilema sobre a extensão da informação a ser armazenada e os métodos de armazenamento. A eficiência computacional é primordial na solução dos problemas concretos que enfrentamos todos os dias. A utilização de normas para a representação números reais na forma de ponto flutuante surgiu como uma resposta. Este artigo desvelará sua funcionalidade e os desafios que esta representação impõe.
Foto de Callie Morgan on Unsplash
Este problema de armazenamento não é exclusivo dos computadores, o caderno que a esforçada leitora usou para aprender a somar era limitado em quantidade de linhas por página e quantidade de páginas por tomo. Nem tudo poderia ser escrito e para tudo que era escrito havia um custo na forma de esforço, tempo e espaço. Perceptível na quantidade de linhas, páginas, tempo de escrita, tempo de localização e tempo de recuperação. Um poema, uma equação, uma resposta. Escritos que, para serem úteis teriam que ser recuperados, lidos e entendidos. Nos oceanos de possibilidades de hardware e software que constituem a computação, não é diferente. Há um custo.
Para que fique claro, e facilite o entendimento, vamos começar nos concentrando nos números decimais, os números escritos na base $10$. Aqueles que a amável leitora conhece deste os tenros tempos da soma nos dedinhos. Porém, entre todos os números possíveis na base $10$, estamos particularmente interessados no conjunto dos Números $reais, $\mathbf{R}$. Os números reais englobam um conjunto vasto de números que incluem:
- Números Inteiros: são números que não têm partes fracionárias, como -3, 0, 1, 2, etc.
- Números Racionais: são números que podem ser expressos como uma fração de inteiros, por exemplo, $\frac{3}{4}$, $\frac{5}{2}$, etc.
- Números Irracionais: são números que não podem ser expressos como uma fração de inteiros e têm uma sequência infinita e não periódica de dígitos após a vírgula decimal. Exemplos são $\pi$ e $\sqrt{2}$.
- Números Decimais: são números que têm uma parte decimal finita ou uma sequência infinita periódica de dígitos após a vírgula decimal.
A categoria que nos interessa mais, no momento, são os números reais fracionários. Estes números podem ser expressos como uma fração de dois inteiros, ou seja, um número racional. Eles podem ser representados na forma de uma fração $\frac{a}{b}$, onde “a” é o numerador e “b” é o denominador (e “b” não é igual a zero). Eles também podem ser representados como decimais finitos ou decimais periódicos. Por exemplo:
\[0.125 = \frac{1}{10}+\frac{2}{100}+\frac{5}{1000} = \frac{1}{10^1}+\frac{2}{10^2}+\frac{5}{10^3}\]“Deus criou os inteiros, todo o resto é trabalho dos homens.” Leopold Kronecker
Não concordo muito com Kronecker. Acho que Deus criou os números naturais, até os números inteiros devem ser contabilizados na coluna da culpa da humanidade. Todos os números fora do conjunto dos Números Naturais, $\mathbb{N}$, estão envolvidos em uma névoa indefinida de teoremas, axiomas e provas matemáticas usados para explicar sua existência, utilidade e coerência. Nós os criamos, e não podemos mais viver sem eles.
Infelizmente, mesmo sob o domínio dos números, errar é humano e, além disso, a exatidão na representação de números reais por meio de operações fracionárias é uma ocorrência rara. O que não é raro é que a representação de números reais, não pode ser completamente realizada, usando números inteiros, mesmo que recorramos ao uso de frações para representar a parte decimal. Esta incompletude na representação de números reais teve um impacto imprevisto e abrangente em todos os sistemas computacionais. Sistemas esses desenvolvidos com base nas ideias de Turing.
Turing, em 1936, concebeu uma máquina, com uma fita infinita e uma cabeça de leitura e escrita. Esta máquina simples resolve qualquer problema que possa ser computado e, com o tempo, esta máquina deu origem a todos os computadores, máquinas de computação, que temos. Estas máquinas modernas substituem a fita por uma pilha de memória. Entretanto, o funcionamento básico é o mesmo. Escrever, correr a fita, ler ou escrever, e repetindo estes passos simples, resolver qualquer problema computacional.
Neste ponto a criativa leitora deve lembrar-se que, em uma célula da memória em um computador, existe apenas um número binário. Um número do Conjunto dos Números Inteiros, $\mathbb{Z}$, escrito na base $2$. E isso é tudo que podemos ter em uma célula de memória. Este é o único conjunto de números que a máquina entende. Não obstante, usamos números reais, textos, imagens, vídeos, sons e tudo mais que podemos imaginar.
Vamos ficar um pouco mais na base decimal, para tentar explicar melhor este problema de representação: como representamos o universo de números reais em um conjunto finito de números inteiros em binário. Tome, por exemplo, a razão $\frac{1}{6}$ e tente representá-la em números reais sem arredondar, ou truncar. Esqueça a calculadora e o computador por um momento.Pegue um lápis e uma folha de papel e tente. Tem pressa não! Eu espero.
Se a esforçada leitora tiver tentado, terá visto, muito rapidamente, que seremos forçados a parar a divisão e arredondar, ou truncar o resultado. Obtendo, invariavelmente, algo como $0.166667$. O ponto em que paramos determina a precisão que usaremos para representar este número e a precisão será, por sua vez, imposta, ou sugerida, apenas pelo uso que daremos a este número. Nesta sentença a palavra uso é a mais importante. É Este uso que definirá o modelo que usaremos para resolver um problema específico. Todos os problemas são diferentes, todos os modelos serão diferentes.
Voltando ao nosso exemplo: fizemos a divisão representada por $\frac{1}{6}$ e encontramos $0.166667$. A multiplicação é a operação inversa de divisão. Logo se multiplicarmos $0.166667 \times 6$ deveríamos encontrar $1$ contudo encontramos: $1.000002$. Um erro de $0.000002$. No seu caderno, prova, ou cabeça, isso é $1$, mas só nestes lugares específicos e fora do alcance dos outros seres humanos. Triste será a sina daquele que não perceber que $1.000002$ é muito diferente de $1$.
Em uma estrada, a diferença de um centímetro que existe entre $12.00 m$ e $12.01 m$ provavelmente não fará qualquer diferença no posicionamento de um veículo. Se estivermos construindo um motor à gasolina, por outro lado, um erro de $1 cm$ será a diferença entre o funcionamento e a explosão. Maximize este conceito imaginando-se no lugar de um um físico que precise utilizar a constante gravitacional. Neste caso, a leitora enfrentará a aventura de fazer contas com números como tão pequenos quanto $0.00000000006667_{10}$.
Graças ao hardware que criamos nos últimos 100 anos, números reais não são adequados ao uso em computação. Pronto falei!
Nossos computadores são binários, trabalham só, e somente só, com números na inteiros na base $2$. Sem pensar muito dá para perceber que existe um número infinito de números reais, representados por um número também infinito de precisões diferentes e que, para que os computadores sejam uteis, todo este universo teve que ser colocado em um espaço restrito definido pela memória disponível e pelas regras da aritmética inteira binária. Não precisa ficar assustada, mas se estiver pensando em ficar assustada a hora é essa.
Assim como os números na base dez, os números reais na base dois podem ser representados por uma parte inteira e uma parte fracionária. Vamos usar o número $0.001_{2}$ como exemplo. Este número pode ser representado por uma operação de frações. Para isso, basta considerar a base $2$:
\[0.001 = \frac{0}{2}+\frac{0}{4}+\frac{1}{8} = \frac{0}{2^1}+\frac{0}{2^2}+\frac{1}{2^3}\]Novamente, sou portador de notícias ruins. Os números fracionários na base $2$ padecem da mesma dor que os números reais na base $10$. A maioria dos números binários facionários, não pode ser representada de forma exata por uma operação de frações. Não bastando isso, a conversão entre as bases $10$ e $2$, acaba criando números binários que não têm fim. Um bom exemplo pode ser visto com a fração $\frac{1}{3}$ que seria representada, em conversão direta para o binário, por $(\frac{1}{11})_2 = 0.0101010101010101_2$ este valor terá que ser arredondado, ou truncado. Esta conversão pode ser vista na Tabela 1:
| Passo | Operação | Resultado Decimal | Parte Inteira | Parte Fracionária (Binário) |
|---|---|---|---|---|
| 1 | $1 \div 3$ | 0.3333... | 0 | 0 |
| 2 | $0.3333... \times 2$ | 0.6666... | 0 | 0 |
| 3 | $0.6666... \times 2$ | 1.3333... | 1 | 01 |
| 4 | $0.3333... \times 2$ | 0.6666... | 0 | 010 |
| 5 | $0.6666... \times 2$ | 1.3333... | 1 | 0101 |
| 6 | $0.3333... \times 2$ | 0.6666... | 0 | 01010 |
| 7 | $0.6666... \times 2$ | 1.3333... | 1 | 010101 |
| 8 | $0.3333... \times 2$ | 0.6666... | 0 | 0101010 |
| 9 | $0.6666... \times 2$ | 1.3333... | 1 | 01010101 |
| 10 | $0.3333... \times 2$ | 0.6666... | 0 | 010101010 |
Definir o ponto onde iremos parar a divisão, determinará a precisão com que conseguiremos representar o valor $(\frac{1}{11})_2$. Além disso, precisaremos encontrar uma forma de armazenar esta representação em memória.
No exemplo dos valores na base decimal que vimos ante, a leitora aprendeu que os valores que aparecem depois da vírgula e que se repetem até o infinito são chamados de dízima, ou dízima periódica. Se por “dízima” entendemos uma sequência que não terminará, então tais números decimais não existem em binário, para que eles existam teremos que parar a divisão e criar uma versão deste número com precisão limitada.
Todos os números reais na base dez, que sejam dízimas, quando representados em binário, também terão repetições infinitas de dígitos. Contudo, há um agravante, muitos números reais exatos, quando convertidos em binário resultam e números com repetições infinitas depois da vírgula.
Só para lembrar: a memória é limitada e contém números inteiros, nosso problema é encontrar uma forma de representar todo o universo de números reais, em base $10$, em um espaço limitado de memória em base $2$. Se pensarmos em uma correspondência de um para um, todo e qualquer número real deve ser armazenado no espaço de dados definido por um e apenas um endereço de memória. Aqui a leitora há de me permitir adiantar um pouco as coisas: esta representação é impossível.
Lá vem o homem com suas imperfeições
Em 1985 o Institute of Electrical and Electronics Engineers (IEEE) publicou uma norma, a norma IEEE 754 cujo objetivo era padronizar uma representação para números de ponto flutuante que deveria ser adotada pelos fabricantes de software e hardware. Na época, os dois mais importantes fabricantes de hardware, Intel e Motorola, apoiaram e adotaram esta norma nas suas máquinas isso foi decisivo para a adoção que disseminada temos hoje. Para os nós interessa que a norma IEEE 754 descreve com representar números com binários com precisão simples, $32 bits$, dupla, $64 bits$, quádrupla $128 bits$ e óctupla $256 bits$. Esta representação é complexa, fria e direta. Talvez fique mais fácil se começarmos lembrando o que é uma notação científica.
Na matemática e nas ciências, frequentemente nos deparamos com números muito grandes ou muito pequenos. Para facilitar a representação e manipulação desses números, utilizamos a notação científica, uma forma especial de expressar números em base $10$. Nesta notação, um número é representado por duas partes: a mantissa e o expoente:
-
A mantissa é a parte significativa do número, que contém os dígitos mais importantes do número que estamos representando.
-
O expoente, $e$, indica a potência a qual a base $10$ deve ser elevada para obter o número original. Assim, a representação geral de um número em notação científica é dada por $\text{mantissa} \times 10^e $.
Para exemplos desta representação veja a Tabela 1.
| Mantissa | Expoente | Notação Científica | Valor em Ponto Fixo |
|---|---|---|---|
| $2.7$ | $4$ | $2.7 \times 10^4$ | $27000$ |
| $-3.501$ | $2$ | $-3.501 \times 10^2$ | $-350.1$ |
| $7$ | $-3$ | $7 \times 10^{-3}$ | $0.007$ |
| $6.667$ | $-11$ | $6.667\times 10^{-11}$ | $0.00000000006667$ |
Uma boa prática no uso da notação científica é deixar apenas um algarismo antes da vírgula e tantos algarismos significativos quanto necessário para o cálculo específico que pretendemos realizar depois da vírgula. Escolhemos a quantidade de números significativos de acordo com a aplicação. Estes algoritmos depois da vírgula terão impacto na precisão do seu cálculo. O $\pi$, com sua infinitude de dígitos depois da vírgula, é um bom exemplo de precisão relativa à aplicação.
Normalmente, um engenheiro civil, ou eletricista, usa o $\pi$ como $3.1416$. Assim mesmo! Arredondando na última casa, pecado dos pecados. A verdade é que quatro algarismos significativos depois da vírgula são suficientemente precisos para resolver a maior parte dos problemas que encontramos no mundo sólido, real, visível e palpável.
Em problemas relacionados com o eletromagnetismo normalmente usamos $\pi = 3.1415926$, igualmente arredondando a última casa mas com $7$ algarismos significativos depois da vírgula. Em problemas relacionados com o estudo da cosmologia usamos $\pi = 3.14159265359$, truncado, sem nenhum arredondamento, com onze algarismos significativos depois da vírgula. Em física de partículas, não é raro trabalhar com 30 dígitos de significativos para $\pi$. A leitora, amável e paciente, pode ler um pouco mais sobre a quantidade de dígitos significativos necessários lendo um artigo do Jet Propulsion Lab.
O melhor uso da notação científica determina o uso de um, e somente um, algarismo antes da vírgula. Além disso, a norma impõe que você não deve usar o zero como único algarismo antes da vírgula. Adotando estas duas regras, $3.1416$ poderia ser representado por $3.1416 \times 10^0$, o que estaria perfeitamente normalizado, ou por $31.416\times 10^{-1}$, uma representação matematicamente válida, mas não normalizada. É importante não esquecer que números que têm $0$ como sua parte inteira não estão normalizados.
Passou pela minha cabeça agora: está claro que a nomenclatura ponto flutuante é importada do inglês? Se fosse em bom português, seria vírgula flutuante. Esta é uma daquelas besteiras que fazemos. Vamos falando, ou escrevendo, estas coisas, sem nos darmos conta que não faz sentido no idioma de Mário Quintana. Herança colonial. Quem sabe?
A base numérica, decimal, hexadecimal, binária, não faz nenhuma diferença na norma da notação científica. Números binários podem ser representados nesta notação tão bem quanto números decimais ou números em qualquer outra base. A leitora pode, por exemplo, usar o número $43.625_{10}$ que, convertido para binário, seria $101011.101_2$ e representá-lo em notação científica como $1.01011101 \times 2^5$. Guarde este número, vamos precisar dele em uma discussão posterior. Sério, guarde mesmo.
“Idealmente, um computador deve ser capaz de resolver qualquer problema matemático com a precisão necessária para este problema específico, sem desperdiçar memória, ou recursos computacionais.” Anônimo.
Por acaso a amável leitora lembra que eu falei da relação de um para um entre um número real e a sua representação em memória? A norma IEEE 754 padronizou a representação binária de números de ponto flutuante e resolveu todos os problemas de compatibilidade entre hardware, software e mesmo entre soluções diferentes que existiam garantindo explicitamente a existência desta relação biunívoca entre o número decimal e o número binário que será usado para armazená-lo em memória. Assim, todas as máquinas, e todos os softwares, entenderam o mesmo conjunto de bits, da mesma forma.
A norma IEEE 754 não é a única forma de armazenar números reais, talvez não seja sequer a melhor forma, mas é de longe a mais utilizada. Com esta norma embaixo do braço, saberemos como representar uma faixa significativa de números reais podendo determinar exatamente a precisão máxima possível para cada valor representado, mesmo em binário e, principalmente, conheceremos todos os problemas inerentes a esta representação. E existem problemas. Afinal, números decimais reais e infinitos serão mapeados em um universo binário, inteiro e finito. O que poderia dar errado?
Quase esqueci! A expressão faixa significativa que usei acima é para destacar que a norma IEEE 754 não permite a representação de todo e qualquer número real. Temos um número infinito de valores na base $10$ representados em um número finito de valores na base $2$.
E os binários entram na dança
Para trabalhar com qualquer valor em um computador, precisamos converter os números reais na base $10$ que usamos diariamente para base $2$ que os computadores usam. Armazenar estes números, realizar cálculos com os binários armazenados e, finalmente converter estes valores para base $10$ de forma que seja possível ao pobre ser humano entender a informação resultante do processo computacional. É neste vai e volta que os limites da norma IEEE 754 são testados e, não raramente, causam alguns espantos e muitos problemas.
Tomemos, por exemplo o número decimal $0.1_{10}$. Usando o Decimal to Floating-Point Converter para poupar tempo, e precisão dupla, já explico isso, podemos ver que:
\[0.1_{10} = (0.0001100110011001100110011001100110011001100110011001101)_2\]Ou seja, nosso $0.1_{10}$ será guardado em memória a partir de:
\[(0.0001100110011001100110011001100110011001100110011001101)_2\]Um belo de um número binário que, será armazenado segundo as regras da norma IEEE 754 e em algum momento será convertido para decimal resultando em:
Eita! Virou outra coisa. Uma coisa bem diferente. Eis porquê em Python, acabamos encontrando coisas como:
>0.1 * 3
>0.30000000000000004
Isto ocorre por que a conta que você realmente fez foi $0.1000000000000000055511151231257827021181583404541015625 \times 3$. Se não acreditar em mim, tente você mesmo, direto na linha de comando do Python ou em alguma célula do Google Colab. Vai encontrar o mesmo erro.
Talvez esta seja uma boa hora para se levantar, tomar um copo d’água e pensar sobre mudança de carreira. Ouvi falar que jornalismo, contabilidade, educação física, podem ser boas opções.
Muitas linguagens de programação, o Python, inclusive, conhecem um conjunto de valores onde erros deste tipo ocorrem e arredondam, ou truncam, o resultado para que você veja o resultado correto. Ou ainda, simplesmente limitam o que é exposto para outras operações, como se estivessem limitando a precisão do cálculo ou dos valores armazenados. Não é raro encontrar linguagens de programação que, por padrão, mostram apenas 3 casas depois da vírgula. Esta foi uma opção pouco criativa adotada por muitos compiladores e interpretadores que acaba criando mais problemas que soluções. Para ver um exemplo, use a fração $\frac{1}{10}$, ainda em Python e reproduza as seguintes operações:
> 1 / 10
>0.1
Viu que lindo? Funciona direitinho. É bem isso que deveria acontecer. A matemática é linda! Os céticos devem experimentar algo um pouco mais complicado, ainda utilizando o Python:
a = 1/10
print( a)
print ("{0:.20f}".format(a))
0.10000000000000000555
E não é que a coisa não é tão linda assim!
A diferença entre estes dois exemplos está na saída. No último formatamos a visualização do resultado para forçar a exibição de mais casas decimais mostrando que o erro está lá. Você não está vendo este erro, o interpretador vai tentar não permitir que este erro se propague, mas ele está lá. E, vai dar problema. E como tudo que causa problemas vai acontecer no pior momento possível.
“Os interpretadores e compiladores são desenvolvidos por seres humanos, tão confiáveis quanto pescadores, caçadores, políticos e advogados. Não acredite em histórias de pescaria, de caçada ou de compilação” Frank de Alcantara.
Isto não é uma exclusividade do Python, a maioria das linguagens de programação, sofre de problemas semelhantes em maior ou menor número. Mesmo que os compiladores e interpretadores se esforcem para não permitir a propagação deste erro se você fizer uma operação com o valor $0.1$, que a linguagem lhe mostra com algum outro valor que exija, digamos $20$ dígitos depois da vírgula o erro estará lá.
Vamos abandonar o computador por um momento. Pegue a sua calculadora e divida um por três e veja o último dígito da tela, se for um seis, sua calculadora trunca a resposta, se for um sete, sua calculadora arredonda. A diferença está na precisão do número representado:
- Truncar: elimina todas as casas decimais após um certo ponto, sem considerar o valor das casas decimais que estão sendo removidas.
- Exemplo:
- Número original: 5.789
- Número truncado (até uma casa decimal): 5.7
- Exemplo:
- Arredondar: aumenta ou diminui o último dígito retido, dependendo do valor do próximo dígito que está sendo removido.
- Exemplo:
- Número original: 5.789
- Número arredondado (até uma casa decimal): 5.8
- Exemplo:
Sistemas, mesmo que sejam simples calculadoras, que arredondam são mais precisos. Existem várias técnicas de arredondamento que não serão objeto deste artigo. Mesmo que eu tenha ficado tentado.
Volte um pouquinho e reveja o que aconteceu, no Python, quando operamos $0.1 * 3$. A leitora deve observar que, neste caso, os dois operandos estão limitados e são exatos. O erro ocorre por que a conversão de $0.1_{10}$ para binário não é exata e somos forçados a parar em algum ponto e, ou truncamos ou arredondamos o valor. Digamos que paramos em: $0.0001100110011001101_2$. Se fizermos isso e convertemos novamente para o decimal o $0.1$ será convertido em $0.1000003814697265625$. E lá temos um baita de um erro. Se a conversão for feita usando os padrões impostos pela IEEE 754 os valores ficam um pouco diferentes, o valor $0.1$ será armazenado em um sistema usando a IEEE 754 como:
-
em precisão simples:
\[00111101 11001100 11001100 11001101_2\] -
em precisão dupla:
\[00111111 10111001 10011001 10011001 10011001 10011001 10011001 10011010_2\]
Que quando convertidos novamente para binário, precisão simples, representará o número $0.100000001490116119385$ isso implica em um erro $256$ vezes menor que o erro que obtemos com a conversão manual e os poucos bits que usamos. Em precisão dupla este valor vai para $0.100000000000000005551_2$ com um erro ainda menor. Nada mal!
Vamos ver se entendemos como esta conversão pode ser realizada usando o $0.1$. Mas antes divirta-se um pouco vendo o resultado que obtemos graças a IEEE 754 para: $0.2$; $0.4$ e $0.8$ usando o excelente Float Point Exposed. Como disse antes: tem pressa não!
Entendendo a IEEE 754
A norma IEEE 754 especifica 5 formatos binários: meia precisão - $16$ bits; precisão simples - $32$ bits; precisão dupla - $64$ bits; precisão quadrupla - $128$ bits e precisão óctupla - $256$ bits. Se olhar com cuidado, exitem algumas variações em torno deste tema. Contudo, por uma questão didática, neste artigo nos ateremos às duas representações de bits mais comumente utilizadas que são as precisões simples e dupla.
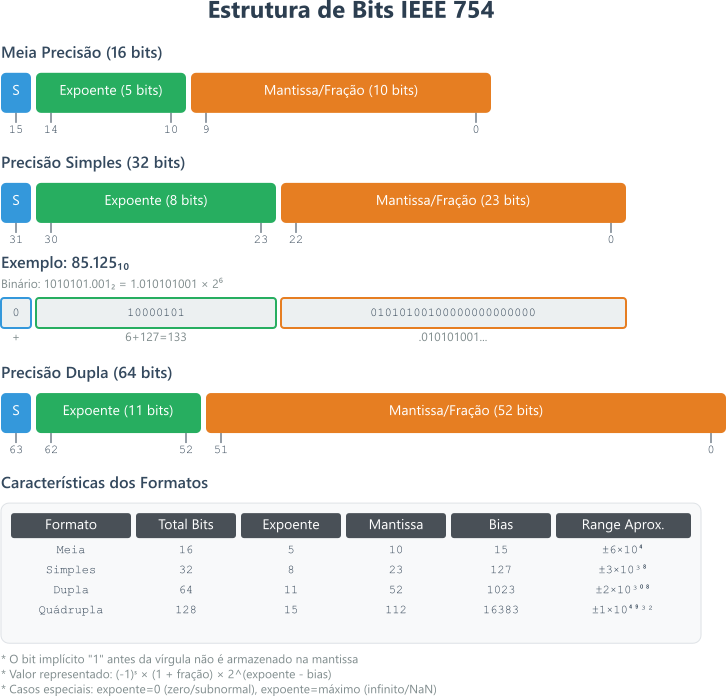 Figura 1. Distribuições de bits segundo a norma IEEE 754, destacando meia precisão, precisão simples e precisão dupla.
Figura 1. Distribuições de bits segundo a norma IEEE 754, destacando meia precisão, precisão simples e precisão dupla.
Um valor real na base $10$, será convertido em binário e ocupará o espaço de $32$, ou $64$ bits, dependendo da precisão escolhida e das capacidades físicas da máquina que irá armazenar este dado. Nos dois casos, o primeiro bit, o bit mais significativo, será reservado para indicar o sinal do número armazenado. Quando encontramos o $1$ neste bit temos a representação de um valor negativo armazenado o zero no bit mais significativo indica um valor positivo. Os próximos $8$ bits, para a precisão simples ou $11$ bits para a precisão dupla, são reservados para o expoente que usaremos para a representação em ponto flutuante. Volto ao expoente já, já. Agora vamos dar uma olhada nos bits que restam além do sinal e do expoente, nestes bits armazenaremos a mantissa, a parte significativa do valor que estamos armazenando.
A terceira seção, que comporta $23$ bits em precisão simples e $52$ em precisão dupla é chamada de mantissa e contém o binário equivalente aos algoritmos significativos do número que vamos armazenar. A leitora deve ser lembrar que eu pedi para guardar o número $1.01011101 \times 2^5$, Lembra? A nossa mantissa, em precisão simples tem espaço para $23$ bits poderíamos, simplesmente, armazenar $10101110100000000000000$. E, neste ponto, temos que parar e pensar um pouco.
Na notação científica, como definimos anteriormente, não podemos ter um zero antes da vírgula. O mesmo deve ser considerado para a notação científica quando usamos números em binário. Com uma grande diferença: se o algarismo antes da vírgula não pode ser um zero ele obrigatoriamente será o $1$. Afinal, estamos falando de binário. Ou seja, a mantissa não precisa armazenar o algarismo antes da vírgula. Sendo assim, para armazenar a mantissa de $1.01011101 \times 2^5$ vamos utilizar apenas $01011101_2$ que resultará em $01011101000000000000000_2$ uma precisão maior graças ao zero a mais. A leitora tinha contado os zeros? Está claro que preenchemos os $32$ bits do mais significativo para o menos significativo por que estamos colocando algoritmos depois da vírgula?
A mantissa é simples e não há muito para explicar ou detalhar. A leitora, se estiver curiosa, pode complementar este conhecimento e ler sobre a relação entre casas decimais em binário e as casas decimais na base dois neste link. Posso apenas adiantar que esta relação tende a $log_2(10) \equiv 3.32$. Isto implica na necessidade de aproximadamente $3.32$ vezes mais algoritmos em binário que em decimal para representar a mesma precisão.
Esta foi a parte fácil, a leitora deve ser preparar para os expoentes. Só para lembrar, temos $8$ bits em precisão simples e $11$ bit em precisão dupla.
Considerando a precisão simples, entre os $8$ bits reservados para a representação do expoente não existe um bit que seja específico para indicar expoentes negativos. Em vez disso, os valores são representados neste espaço de $8$ bits em uma notação chamada de excess-127 ou bias. Nesta notação, utilizamos um número inteiro de $8$ bits cujo valor sem sinal é representado por $M-127$ como expoente. Desta forma, O valor $01111111$ equivalente ao valor $127$ representa o expoente $0$ em decimal, o valor $01000000$ equivalente a $128$, representa o expoente $1$, enquanto o valor $01111110$ equivalente a $126$ representa o expoente $-1$ e por ai vamos. Em outras palavras, para representar o expoente $0$ armazenamos o valor binário $M=01111111$ equivalente ao $127$ e o expoente será dado por \(M\) subtraído do valor $127$, ou seja $0$. Usando esta técnica excess-127 ou bias teremos uma faixa de expoentes que variam $2^{-126}$ e $2^{128}$ para a precisão simples. Parece complicado e é mesmo.
No caso da precisão dupla o raciocínio é exatamente o mesmo exceto que o espaço é de $11$ bits e o bias é de $1023 (excess-1023)$. Com $11$ bits conseguimos representar valores entre $0$ e $2047$. Neste caso, o $M=1023$ irá representar o valor $0$. Com a precisão dupla poderemos representar expoentes entre $-1022$ e $1023$. Em resumo:
-
em precisão simples um expoente estará na faixa entre $-126$ e $127$ com um bias de $127$ o que permitirá o uso de algoritmos entre $1$ e $254$, os valores $0$ e $255$ são reservados para representações especiais;
-
em precisão dupla um expoente estará na faixa entre $-1022$ e $1023$ com um bias de $1023$ o que permitirá o uso de valores entre $1$ e $2046$, os valores $0$ e $2047$ são reservados para representações especiais.
Parafraseando um dos personagens do filme Bolt, a leitora deve colocar um pin na frase: são reservados para representações especiais nós vamos voltar a isso mais trade. Por enquanto vamos voltar ao $0.1_{10}$. Este é valor numérico que mais irrita todo mundo que estuda este tópico. Deveria ser simples é acaba sendo muito complexo.
De decimal para IEEE 754 na unha
A compassiva leitora terá que me dar um desconto, vou fazer em precisão simples. Haja zeros! E, por favor, preste atenção só vou fazer uma vez.
Antes de qualquer relação com a norma IEEE 754, vamos converter $0.1_{10}$ para binário. Começamos pela parte inteira deste número. Para isso vamos dividir o número inteiro repetidamente por dois, armazenar cada resto e parar quando o resultado da divisão, o quociente, for igual a zero e usar todos os restos para representar o número binário:
Esta parte foi fácil $0_{10}$ é igual a $0_2$.
Em seguida precisamos converter a parte fracionária do número $0.1$ multiplicando este algoritmo repetidamente por dois até que a parte fracionária, aquilo que fica depois da vírgula, seja igual a zero e já vamos separando a parte inteira, resultado da multiplicação da parte fracionária. Vamos armazenar a parte inteira enquanto estamos multiplicando por dois a parte fracionária do resultado de cada operação anterior. Ou seja, começamos com $0.1 \times 2 = 0.2$ temos $0$ parte inteira do resultado da multiplicação e $0.2$ parte fracionária do resultado que vamos representar por $0.1 \times 2 = 0 + 0.2$ e assim sucessivamente:
| 1. | $0.1 × 2 = 0 + 0.2$ | 13. | $0.2 × 2 = 0 + 0.4$ |
| 2. | $0.2 × 2 = 0 + 0.4$ | 14. | $0.4 × 2 = 0 + 0.8$ |
| 3. | $0.4 × 2 = 0 + 0.8$ | 15. | $0.8 × 2 = 1 + 0.6$ |
| 4. | $0.8 × 2 = 1 + 0.6$ | 16. | $0.6 × 2 = 1 + 0.2$ |
| 5. | $0.6 × 2 = 1 + 0.2$ | 17. | $0.4 × 2 = 0 + 0.8$ |
| 6. | $0.4 × 2 = 0 + 0.8$ | 18. | $0.8 × 2 = 1 + 0.6$ |
| 7. | $0.8 × 2 = 1 + 0.6$ | 19. | $0.6 × 2 = 1 + 0.2$ |
| 8. | $0.6 × 2 = 1 + 0.2$ | 20. | $0.2 × 2 = 0 + 0.4$ |
| 9. | $0.2 × 2 = 0 + 0.4$ | 21. | $0.4 × 2 = 0 + 0.8$ |
| 10. | $0.4 × 2 = 0 + 0.8$ | 22. | $0.8 × 2 = 1 + 0.6$ |
| 11. | $0.8 × 2 = 1 + 0.6$ | 23. | $0.6 × 2 = 1 + 0.2$ |
| 12. | $0.6 × 2 = 1 + 0.2$ | 24. | $0.2 × 2 = 0 + 0.4$ |
| 25. | $0.4 × 2 = 0 + 0.8$ |
Podemos continuar e não vamos conseguir encontrar um resultado de multiplicação cuja parte fracionária seja igual a $0$, contudo como na mantissa, em precisão simples, cabem 23 bits, acho que já chegamos a um nível suficiente de precisão. Precisamos agora ordenar todas as partes inteiras que encontramos para formar nosso binário:
\[0.1_{10} = 0.000110011001100110011001100_2\] Figura 2: Algoritmo e todos os passos da conversão de 0.1 na base 10 em binário.
Figura 2: Algoritmo e todos os passos da conversão de 0.1 na base 10 em binário.
Resta normalizar este número. A leitora deve lembrar que a representação normal, não permite o $0$ como algarismo inteiro (antes da vírgula). O primeiro $1$ encontra-se na quarta posição logo:
\[0.0001 1001 1001 1001 1001 1001 100_2 \\ = 1.1001 1001 1001 1001 1001 100_2 \times 2^{-4}\]Precisamos agora normalizar nosso expoente. Como estamos trabalhando com precisão simples usaremos $127$ como bias. Como temos $-4$ teremos $(-4+127) = 123$ que precisa ser convertido para binário. Logo nosso expoente será $01111011$.
Até agora temos o sinal do número, $0$ e o expoente $01111011$ resta-nos terminar de trabalhar a mantissa. Podemos remover a parte inteira já que em binário esta será sempre $1$ devido ao $0$ não ser permitido. Feito isso, precisamos ajustar seu comprimento para $23$ bits e, temos nossa mantissa: $10011001100110011001100$. Linda! E resumo temos:
| Elemento | Valor |
|---|---|
| Sinal | $(+) = 1$ |
| Expoente | $(123_{10}) = 01111011_2$ |
| Mantissa | $10011001100110011001100$ |
| Total | $32 \space bits$ |
Os valores especiais
A leitora deve lembrar da expressão que pedi que colocasse um pin: são reservados para representações especiais. Está na hora de tocar neste assunto delicado. A verdade é que não utilizamos a IEEE 754 apenas para números propriamente ditos, utilizamos para representar todos os valores possíveis de representação em um ambiente computacional que sejam relacionados a aritmética dos números reais. Isto quer dizer que temos que armazenar o zero, o infinito e valores que não são numéricos, os famosos NAN, abreviação da expressão em inglês Not A Number que em tradução livre significa não é um número. A forma como armazenamos estes valores especiais estão sintetizados na tabela a seguir:
| Precisão Simples | Precisão Dupla | |||
|---|---|---|---|---|
| Expoente | Mantissa | Expoente | Mantissa | Valor Representado |
| $0$ | $0$ | $0$ | $0$ | $\pm 0$ |
| $0$ | $ \neq 0$ | $0$ | $ \neq 0$ | $\pm \space Número \space Subnormal$ |
| $1-254$ | $Qualquer \space valor$ | $1-2046$ | $Qualquer \space valor$ | $\pm \space Número \space Normal $ |
| $255$ | $0$ | $2047$ | $0$ | $\pm \space Infinito$ |
| $255$ | $\neq 0$ | $2047$ | $\neq 0$ | $NaN \space (Not \space a \space Number)$ |
Resta-nos entender o que estes valores representam e seu impacto na computação.
Números subnormais
Para a IEEE 754 normal é tudo que vimos anteriormente, todos os valores que podem ser representados usando as regras de sinal, expoente e mantissa de forma normalizada que a amável leitora teve a paciência de estudar junto comigo. Subnormal, ou não normalizado, é o termo que empregamos para indicar valores nos quais o campo expoente é preenchido com zeros. Se seguirmos a regra, para representar o algarismo $0$ o expoente deveria ser o $-127$. Contudo, para este caso, onde todo o campo expoente é preenchido com $00000000$ o expoente será $-126$. Neste caso especial, a mantissa não terá que seguir a obrigatoriedade de ter sempre o número $1$ como parte inteira. Não estamos falando de valores normalizados então o primeiro bit pode ser $0$ ou $1$. Estes números foram especialmente criados para aumentar a precisão na representação de números que estão no intervalo entre $0$ e $1$ melhorando a representação do conjunto dos números reais nesta faixa.
A leitora há de me perdoar novamente, a expressão subnormal é típica da norma IEEE 854 e não da IEEE 754, mas tomei a liberdade de usar esta expressão aqui por causa da melhor tradução.
Zero
Observe que a definição de zero na norma IEEE 754 usa apenas o expoente e a mantissa e não altera nada no bit que é utilizado para indicar o sinal de um número. A consequência disto é que temos dois números binários diferentes um para $+0$ e outro para $-0$. A leitora deve pensar no zero como sendo apenas outro número subnormal que, neste caso acontece quando o expoente é $0$ e a mantissa é $0$. Sinalizar o zero não faz sentido matematicamente e tanto o $+0$ quanto o $-0$ representam o mesmo valor. Por outro lado, faz muita diferença do ponto de vista computacional e é preciso atenção para entender estas diferenças.
Infinito
Outro caso especial do campo de exponentes é representado pelo valor $11111111$. Se o expoente for composto de $8$ algarismos $1$ e a mantissa for totalmente preenchida como $0$, então o valor representado será o infinito. Acompanhando o zero, o infinito pode ser negativo, ou positivo.
Neste caso, faz sentido matematicamente. Ou quase faz sentido. Não, não faz sentido nenhum! Não espere, faz sim! Droga infinito é complicado. A verdade é que ainda existem muitas controvérsias sobre os conceitos de infinito, mesmo os matemáticos não tem consenso sobre isso, a norma IEEE 754 com o $\pm Infinito$ atende ao entendimento médio do que representa o infinito.
Se você está usando uma linguagem de programação que segue a norma IEEE 754, você notará algo interessante ao calcular o inverso de zero. Se fizer o cálculo com $-0$, o resultado será $-\infty$. Se fizer o cálculo com $+0$, o resultado será $+\infty$.
Do ponto de vista estritamente matemático, isso não é exatamente correto. Matematicamente, a divisão de qualquer número por zero não é definida - diz-se que ela tende ao infinito, mas não é igual ao infinito.
O que a norma IEEE 754 está fazendo aqui é uma espécie de compromisso prático. Ela nos dá uma indicação da direção em que o resultado está indo (para o infinito positivo ou negativo), mesmo que isso não seja uma representação exata do que acontece na matemática pura. Assim, em termos de programação, obtemos uma resposta útil, mesmo que essa resposta não seja rigorosamente precisa do ponto de vista matemático.
NaN (Not a Number)
O conceito de NaN foi criado para representar valores, principalmente resultados, que não correspondem a um dos números reais que podem ser representados em binário segundo a norma IEEE 754. Neste caso o expoente será completamente preenchido como $1$ e a mantissa será preenchida com qualquer valor desde que este valor não seja composto de todos os algarismos com o valor $0$. O bit relativo ao sinal não causa efeito no NaN. No entanto, existem duas categorias de NaN: QNaN (Quiet NaN) e SNaN (Signalling NaN).
O primeiro caso QNaN, (Quiet NaN), ocorre quando o bit mais significativo da mantissa é $12$. O QNaN se propaga na maior parte das operações aritméticas e é utilizado para indicar que o resultado de uma determinada operação não é matematicamente definido. já o SNaN, _(Signalling NaN), que ocorre quando o bit mais significativo da mantissa é $0_2$ é utilizado para sinalizar alguma exceção como o uso de variáveis não inicializadas. Podemos sintetizar estes conceitos memorizando que QNaN indica operações indeterminadas enquanto SNaN indica operações inválidas.
| Operação | Resultado |
|---|---|
| $(Número) \div (\pm \infty)$ | $0$ |
| $(\pm \infty) \times (\pm \infty)$ | $\pm \infty$ |
| $(\pm \neq 0) \div (\pm 0)$ | $\pm \infty$ |
| $(\pm Número) \times (\pm \infty)$ | $\pm \infty$ |
| $(\infty) + (\infty)$ | $+\infty$ |
| $(\infty) - (-\infty)$ | $+\infty$ |
| $(-\infty) + (-\infty)$ | $-\infty$ |
| $(-\infty) - (\infty)$ | $-\infty$ |
| $(\infty) - (\infty)$ | `NaN` |
| $(-\infty) + (\infty)$ | `NaN` |
| $(\pm 0) \div (\pm 0)$ | `NaN` |
| $(\pm \infty) \div (\pm \infty)$ | `NaN` |
| $(\pm \infty) \times (0)$ | `NaN` |
| $(NaN) == (NaN)$ | $false$ |
Antes de chamar os aldeões e começar a acender fogueiras a paciente leitora precisa levar em consideração as intensões que suportam a norma IEEE 754: o objetivo original, e inocente, era criar uma estrutura de regras e métodos padrão para a troca de números em ponto flutuante entre máquinas e softwares diversos. Resolvendo milhares de problemas de compatibilidade que impediam o progresso da computação. E só. Era só isso.
No esforço que criar uma camada de compatibilidade, foi criado um padrão eficiente, limitado e complexo que permite operar com números de ponto flutuante, números reais, com um grau de precisão aceitável para a imensa maioria das operações computacionais.
Durante a criação da norma, ninguém se preocupou muito que valores especiais como $\pm Infinito$ ou NaN seriam usados para qualquer coisa diferente de criar interrupções e sinalizar erros. Foi o tempo que apresentou situações interessantes que precisaram de detalhamento da norma. Notadamente quando passamos a exigir dos nossos programas comportamentos numericamente corretos para a resolução de problemas complexos.
O $-0$ e o $+0$ representam exatamente o mesmo valor mas são diferentes $-0 \neq +0$ o que implica que em alguns casos, nos quais, mesmo que $x=y$ eventualmente podemos ter que $\frac{1}{x} \neq \frac{1}{y}$ para isso basta que algum momento durante o processo de computação $x=-0$ e $y=+0$ o que já é suficiente para criar uma grande quantidade de problemas. Antes de achar que isso é muito difícil lembre-se, por favor, que existe um número próximo do infinito, só para ficar no dialeto que estamos usando, de funções que cruzam os eixos de um plano cartesiano. Um ponto antes estas funções estarão em $-0$ e um ponto depois em $+0$. Se tratarmos a existência do $\pm 0$ como interrupção ou alerta, podemos gerir estas ocorrências eficientemente e manter a integridade da matemática em nossos programas. Na matemática $+0$ e $-0$ são tratados da mesma forma. Se formos observar cuidadosamente os cálculo e utilizar estes dois valores de zero de forma diferente então, teremos que prestar muita atenção nas equações que usaremos em nossos programas.
O infinito é outro problema. Pobres de nós! Estes conceitos foram inseridos na norma para permitir a concordância com a ideia que o infinito é uma quantidade, maior que qualquer quantidade possivelmente representada e atende a Teoria Axiomática de Zermelo–Fraenkel. Isto é importante porque hoje, esta é a teoria axiomática da teoria dos conjuntos que suporta toda a matemática. Vamos deixar Zermelo–Fraenkel para um outro artigo já que este conhecimento não faz parte do cabedal de conhecimentos do programador mediano. Basta lembrar que as operações aritméticas são coerentes e que, na maior parte das linguagens é possível trabalhar isso como um alerta.
Por fim, temos o NaN este valor indica uma operação inválida, como $0 \div 0$ ou $\sqrt(-1)$. Este valor será propagado ao longo da computação, assim que surgir como resultado, permitindo que a maioria das operações que resultem em NaN, ou usem este valor como operador, disparem algum tipo de interrupção, ou alerta, que indique que estamos trabalhando fora dos limites da matemática e, muitas vezes, da lógica. Novamente, os problemas ocorrem graças as decisões que tomamos quando criamos uma linguagem de programação. Hoje não é raro encontrar programas onde o valor $NaN$ seja utilizado como um valor qualquer inclusive em operações de comparação. Pobres de nós!
Além disso tudo, como existem limitações na representação de números reais, é possível que dois números diferentes sejam representados pelo mesmo valor binário. Por exemplo,
\[0.1_{10}\]e
\[0.2_{10}\]não podem ser representados exatamente em binário, então eles são aproximados para o valor mais próximo que pode ser representado. Isso pode levar a erros de arredondamento e comparações inesperadas. Ou seja, existem falhas no range de valores que podem ser representados, o que pode levar a erros de precisão e comparações inesperadas.
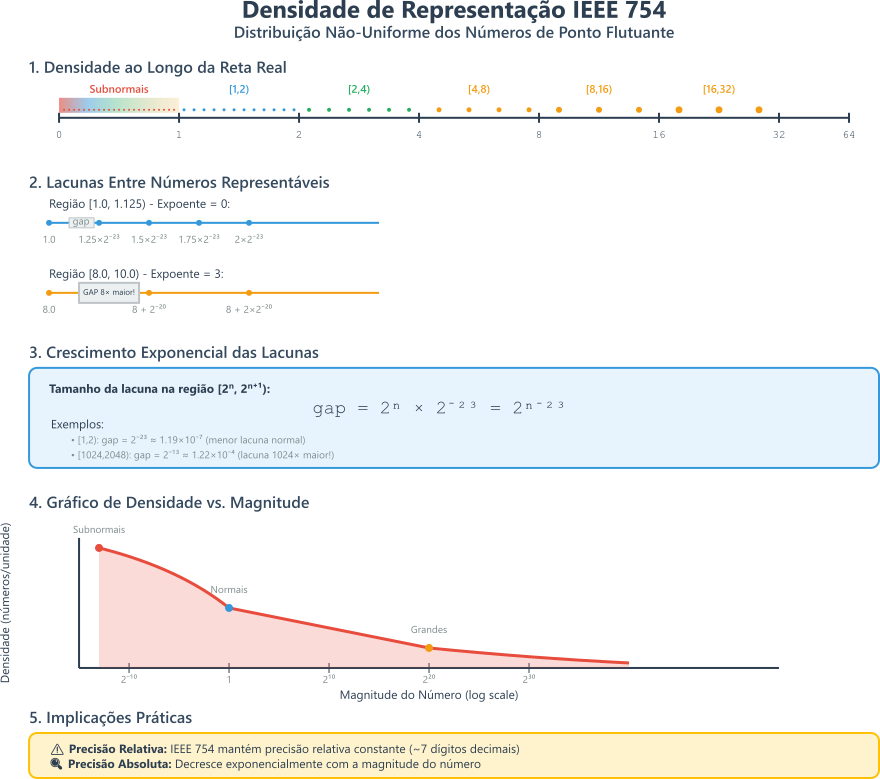 Figura 3: Densidade de distribuição de números segundo a norma IEEE 754
Figura 3: Densidade de distribuição de números segundo a norma IEEE 754
Esta aritmética foi criada para que qualquer programador, mesmo o mais ignorante, fosse avisado de que algo estava fora do normal e não para que os meandros da teoria dos números fossem explorados. William Kahan.
A leitora deve fazer um esforço para me compreender nesta última citação. Não é uma citação literal, trata-se de uma paráfrase de um dos criadores da norma IEEE 754. Entendendo a intensão que suporta o ato, entendemos as consequências deste ato. A norma permite o uso de valores de forma algebricamente correta. E isto deveria bastar. Até que a gente encontra linguagens como o javascript.
> typeof NaN
> "number"
> NaN = NaN
> false;
As duas operações estão perfeitamente corretas segundo a norma, mas não fazem nenhum sentido, pelo menos não para quem ignora a norma. Sim, realmente NaN é um número e sim, $NaN = NaN$ é falso. Em Javascript: the weird parts Charlie Harvey explora muitas das incongruências encontradas no javascript apenas porque os interpretadores seguem rigidamente as normas sem atentar para as razões da existência destas normas.
Aqui eu usei exemplos do Python e do Javascript porque são mais fáceis de testar. Nenhuma linguagem de programação imperativa está livre destes problemas. Se quiser dar uma olhada em C++, no Windows, John D. Cook em IEEE floating-point exceptions in C++ mostra como fazer isso.
Uma coisa deve ficar para sempre: não use pontos flutuantes para dinheiro e nunca use float se o double estiver disponível. Só use float se estiver escrevendo programas em ambientes muito, muito, muito limitados em memória.
Certa vez Joel Spolsky criou o termo leaky abstraction que eu aqui, em tradução livre vou chamar de abstração fraca. A computação é toda baseada em metáforas e abstrações. Uma abstração forte é aquela em que você usa uma ferramenta sem nunca ter que abrir e ver o que há lá dentro. Uma abstração fraca é aquela em que você tem que abrir a ferramenta antes de usar. Pontos flutuantes são abstrações fracas. E, apesar de todas as linguagens de programação que eu conheço usarem esta norma, a leitora não está obrigada a usar esta norma nos seus programas, mas isto é assunto para outro artigo.
Implementação da Aritmética de Ponto Flutuante IEEE 754
Só para lembrar, o padrão IEEE 754 representa números de ponto flutuante como $V=(-1)^s \times M \times 2^E$, onde $s$ é o bit de sinal, $M$ é o significando (mantissa) e $E$ é o expoente com bias. O padrão define múltiplos formatos de precisão, sendo a precisão simples (32 bits) e a precisão dupla (64 bits) as mais comuns. A precisão simples usa $1$ bit de sinal, $8$ bits de expoente (com bias de $+127$) e $23$ bits de mantissa mais um bit $1$ implícito. A precisão dupla estende isso para $11$ bits de expoente, com bias de $+1023$, e $52$ bits de mantissa.# Algoritmos de Arredondamento IEEE 754
A norma IEEE 754 define cinco modos de arredondamento obrigatórios que determinam como valores intermediários são convertidos para a representação de ponto flutuante mais próxima. Cada modo possui características específicas que afetam a precisão e o comportamento numérico das operações.
Modos de Arredondamento Definidos na Norma
Antes de enfrentarmos os algoritmos e técnicas usados nas operações aritméticas de ponto flutuante, é importante entender os modos de arredondamento definidos na norma IEEE 754. Estes modos determinam como os números são arredondados durante as operações aritméticas e influenciam diretamente a precisão dos resultados. A norma define cinco modos de arredondamento, cada um com seu próprio comportamento e nome técnico. Estes modos são:
1. Round to Nearest, Ties to Even (Padrão)
Nome técnico: roundTiesToEven
Comportamento: arredonda para o valor representável mais próximo. Em caso de empate, quando o valor está exatamente no meio de dois representáveis, arredonda para o valor com bit menos significativo par.
2. Round to Nearest, Ties Away from Zero
Nome técnico: roundTiesToAway
Comportamento: arredonda para o valor representável mais próximo. Em caso de empate, arredonda para longe do zero, valor com maior magnitude absoluta.
3. Round Toward Positive Infinity
Nome técnico: roundTowardPositive
Comportamento: sempre arredonda em direção ao $+\infty$. Para valores positivos, arredonda para cima; para valores negativos, arredonda para baixo, em direção ao zero.
4. Round Toward Negative Infinity
Nome técnico: roundTowardNegative
Comportamento: sempre arredonda em direção ao $-\infty$. Para valores positivos, arredonda para baixo, em direção ao zero; para valores negativos, arredonda para baixo, aumentando magnitude.
5. Round Toward Zero
Nome técnico: roundTowardZero
Comportamento: sempre arredonda em direção ao zero, efetivamente truncando a parte fracionária. Equivale ao comportamento de conversão de inteiros em muitas linguagens.
Algoritmo Round to Nearest, Ties to Even (Mais Comum)
O modo roundTiesToEven é o padrão da norma IEEE 754 e o mais amplamente utilizado devido às suas propriedades estatísticas superiores. Este algoritmo minimiza o erro de arredondamento acumulado em sequências longas de operações apresentando um comportamento mais previsível e equilibrado. Em geral podemos destacar as seguintes vantagens:
- Redução de viés estatístico: em sequências longas de operações, o número de arredondamentos para cima e para baixo tende a se equilibrar;
- Propriedade de convergência: minimiza o erro acumulado em cálculos extensos;
- Compatibilidade: padrão universalmente aceito, garantindo portabilidade entre sistemas;
Este algoritmo pode ser demonstrado como sendo o melhor método para a maioria das aplicações numéricas.
O algoritmo de roundTiesToEven, utiliza três bits extras preservados durante o alinhamento de expoentes, a saber:
- Guard bit (G): primeiro bit após a mantissa. O guard bit é o bit imediatamente após a mantissa representável, usado para preservar precisão durante o arredondamento.Na verdade, o guard bit é o primeiro bit que seria descartado após os bits da mantissa representável, ou seja, o bit na posição imediatamente após os $23$ bits da mantissa em precisão simples;
- Round bit (R): segundo bit após a mantissa;
- Sticky bit (S): $OR$ lógico de todos os bits restantes.
O sticky bit (S) é definido como o $OR$ lógico de todos os bits que são descartados durante um deslocamento à direita da mantissa, geralmente no processo de alinhamento de expoentes ou normalização. Este bit serve para indicar se algum bit significativo foi perdido, garantindo que a decisão de arredondamento reflita qualquer contribuição de bits menos significativos.
Considere uma mantissa representada por $26$ bits, $23$ bits da mantissa
IEEE 754em precisão simples mais $3$ bits extras para precisão intermediária, que precisa ser deslocada $3$ posições à direita para alinhar expoentes:
- Mantissa inicial:
1.10110010011001000000000010;- Deslocamento de 3 bits à direita: Os $3$ bits menos significativos são deslocados para fora da mantissa representável.
Passo a passo:
- Os bits descartados são:
010(os últimos 3 bits);- O sticky bit é calculado como o OR lógico desses bits: $ 0 \lor 1 \lor 0 = 1$;
- Resultado após deslocamento: A mantissa torna-se
1.10110010011001000000000, com sticky bit =1.Se todos os bits descartados fossem
0(ex.:000), o sticky bit seria0. Esse valor é usado nas regras de arredondamento para determinar se $GRS > 0.5$ ou $GRS = 0.5$.
O arredondamento segue a seguinte lógica hierárquica:
- Caso 1: se $R = 0$, então $GRS < 0.5$ → não arredonda;
- Caso 2: se $R = 1$ e $S = 1$, então $GRS > 0.5$ → arredonda para cima;
- Caso 3: se $R = 1$ e $S = 0$, então $GRS = 0.5$ → empate:
- Se LSB da mantissa = 0 (par) → não arredonda;
- Se LSB da mantissa = 1 (ímpar) → arredonda para cima.
Formalização Matemática
\[\text{round\_up} = R \land (S \lor \text{LSB})\]na qual:
- $R$: Round bit
- $S$: Sticky bit
- $\text{LSB}$: Bit menos significativo da mantissa
 Figura 4: Processo de preservação de precisão e arredondamento IEEE 754 usando os bits Gard, Round e Sticky
Figura 4: Processo de preservação de precisão e arredondamento IEEE 754 usando os bits Gard, Round e Sticky
Exemplos Práticos
Exemplo 1: Mantissa = 1.10110, GRS = 100
- $R = 0$ → Não arredonda. Ou seja, como $R = 0$, não arredonda, independentemente de $G$ ou $S$;
- Resultado:
1.10110.
Exemplo 2: Mantissa = 1.10110, GRS = 110
- $R = 1$, $S = 0$ → Empate;
- LSB = 0 (par) → Não arredonda;
- Resultado:
1.10110.
Exemplo 3: Mantissa = 1.10111, GRS = 100
- $R = 0$ → Não arredonda;
- Resultado:
1.10111.
Exemplo 4: Mantissa = 1.10111, GRS = 110
- $R = 1$, $S = 0$ → Empate. Como $R = 1$, $S = 0$, temos $GRS = 0.5$. Como o $LSB$ da mantissa é $1$ (ímpar), arredonda para cima;
- LSB = 1 (ímpar) → Arredonda para cima;
- Resultado:
1.11000.
Exemplo 5: Mantissa = 1.10110, GRS = 101
- $R = 1$, $S = 1$ → GRS > 0.5 → Arredonda para cima;
- Resultado:
1.10111.
Implementação em Pseudocódigo
FUNÇÃO round_to_nearest_ties_to_even(mantissa, guard, round, sticky, expoente):
// Constantes
MANTISSA_BITS = 23 // Para precisão simples; 52 para precisão dupla
// Caso básico: round bit = 0
SE round == 0:
RETORNA mantissa, expoente // Não arredonda
// Caso: round bit = 1
SE sticky == 1:
// GRS > 0.5, sempre arredonda para cima
mantissa = mantissa + 1
SENÃO:
// GRS = 0.5 exato (empate)
lsb = mantissa AND 1
SE lsb == 0:
RETORNA mantissa, expoente // Par, não arredonda
SENÃO:
mantissa = mantissa + 1 // Ímpar, arredonda para cima
// Verifica overflow após arredondamento
SE mantissa >= 2^(MANTISSA_BITS + 1):
mantissa = mantissa >> 1
expoente = expoente + 1
RETORNA mantissa, expoente
Casos Especiais
- Overflow após arredondamento: se o arredondamento causar overflow na mantissa, desloca-se à direita e incrementa-se o expoente;
- Transição para infinito: se o expoente exceder o limite após normalização, o resultado torna-se infinito;
- Números denormalizados: o algoritmo funciona similarmente, mas sem o bit implícito.
O algoritmo roundTiesToEven representa um equilíbrio cuidadoso entre precisão, performance e previsibilidade, sendo fundamental para a confiabilidade dos sistemas de ponto flutuante modernos. Vamos usá-lo imediatamente na implementação da aritmética de ponto flutuante.
Implementação de adição e subtração
O algoritmo de adição do IEEE 754 produz resultados exatamente arredondados por meio de uma sequência de operações cuidadosamente orquestrada. O principal desafio reside em alinhar operandos com expoentes diferentes, preservando a precisão.
O algoritmo começa com a detecção de casos especiais, verificando se há operandos NaN, infinito ou zero. Quando ambos os operandos são finitos, a implementação compara os expoentes e identifica qual operando tem a menor magnitude. O significando do operando menor passa por um deslocamento para a direita para se alinhar com o expoente do operando maior.
O alinhamento do expoente representa a fase mais sensível em termos de precisão. A implementação calcula a diferença $\vert E_A - E_B \vert$ e desloca a mantissa do operando menor para a direita por essa quantidade. Cada deslocamento para a direita aumenta efetivamente o expoente desse operando em 1, trazendo ambos os operandos para a mesma base de expoente. Durante este processo, os bits de guarda (guard), arredondamento (round) e aderente (sticky) preservam informações de precisão que seriam perdidas de outra forma.
Após o alinhamento, a implementação realiza a adição ou subtração dos significandos nas mantissas alinhadas. Isso pode produzir um transporte de saída, exigindo normalização, ou zeros à esquerda, exigindo deslocamentos para a esquerda. O passo de normalização garante que o resultado mantenha a forma padrão $1.xxx \times 2^E$, ajustando tanto a mantissa quanto o expoente.
Podemos detalhar o algoritmo de adição e subtração do IEEE 754 em seis etapas principais:
1. Tratamento de Casos Especiais
O algoritmo primeiro trata valores excepcionais conforme as especificações IEEE 754:
- Propagação de
NaN: se qualquer operando éNaN, retornaNaN; - Casos de infinito: $\pm\infty + \pm\infty$ segue regras de sinal; $\infty - \infty$ produz
NaN; - Tratamento de zero: adição com zero retorna o operando não-zero; subtração pode produzir zero positivo ou negativo.
2. Extração de Componentes
Para operandos finitos não-zero, extraímos os componentes:
\[\text{Operando} = (-1)^s \times 1.f \times 2^{e-\text{bias}}\]Na qual:
- $s$: bit de sinal;
- $f$: fração (mantissa sem o bit implícito);
- $e$: expoente enviesado;
- Para precisão simples: bias = $127$, para dupla: bias = $1023$.
3. Alinhamento de Expoentes
Esta é a etapa crítica para preservação da precisão:
- Comparação de expoentes: Determina qual operando tem menor magnitude comparando os expoentes $E_A$ e $ E_B$;
-
Cálculo do deslocamento: Calcula a diferença $ \text{shift} = E_A - E_B $; - Deslocamento à direita: A mantissa do operando com menor expoente é deslocada à direita por $ \text{shift}$ posições para alinhar os expoentes;
- Preservação de bits extras: Durante o deslocamento, são preservados dois bits de guarda (guard e round) e o sticky bit. O guard bit é o primeiro bit descartado após a mantissa representável, o round bit é o segundo bit descartado, e o sticky bit é o OR lógico de todos os bits subsequentes descartados. Esses bits extras são essenciais para manter a precisão e aplicar as regras de arredondamento (como
roundTiesToEven) posteriormente.
4. Operação Aritmética
Dependendo dos sinais dos operandos:
- Mesmos sinais: adição efetiva das mantissas;
- Sinais opostos: subtração efetiva, pode exigir complemento de dois.
5. Normalização
O resultado pode exigir normalização:
- Overflow da mantissa: desloca à direita e incrementa expoente;
- Underflow da mantissa: desloca à esquerda e decrementa expoente;
- Detecção de zeros à esquerda: conta e remove zeros leading.
Por que a Normalização é Necessária
A normalização é necessária porque a operação aritmética (adição ou subtração) pode produzir resultados que não estão na forma normalizada
IEEE 754, que exige mantissa na forma $1.xxx \times 2^E$.Por que ocorre cada caso:
Overflow da mantissa acontece quando:
- Soma de duas mantissas normalizadas (ambas $\geq 1.0$) resulta em valor $\geq 2.0$;
- Exemplo: $1.8 + 1.7 = 3.5$, que excede o formato $1.xxx$;
- Solução: Desloca mantissa 1 bit à direita e incrementa expoente;
- $3.5 \times 2^n$ torna-se $1.75 \times 2^{n+1}$.
Underflow da mantissa ocorre quando:
- Subtração de números próximos resulta em mantissa $< 1.0$;
- Exemplo: $1.001 - 1.000 = 0.001$, que não está na forma $1.xxx$;
- Solução: Desloca mantissa à esquerda até o bit mais significativo estar na posição correta, decrementando o expoente correspondentemente;
- $0.001 \times 2^n$ pode tornar-se $1.024 \times 2^{n-10}$ (após 10 deslocamentos).
Detecção de zeros à esquerda surge do cancelamento catastrófico:
- Subtração de números muito próximos elimina bits significativos;
- Exemplo: $1.00000001 - 1.00000000 = 0.00000001$;
- Múltiplos zeros à esquerda precisam ser removidos para restaurar a forma $1.xxx$;
- Processo: Conta quantos deslocamentos à esquerda são necessários e ajusta o expoente adequadamente.
A normalização garante que o resultado final mantenha a representação padrão
IEEE 754, preservando a precisão máxima possível e evitando representações ambíguas.
 Figura 6: Regras de normalização da norma IEEE 754
Figura 6: Regras de normalização da norma IEEE 754
6. Arredondamento
Aplica-se o modo de arredondamento (geralmente “round to nearest, ties to even”) usando os bits extras preservados.
Pseudocódigo e Fluxograma para Adição e Subtração
A seguir, apresentamos o pseudocódigo para a implementação da adição e subtração de números em ponto flutuante segundo a norma IEEE 754. O fluxograma ilustra as etapas do algoritmo, desde o tratamento de casos especiais até o arredondamento final.
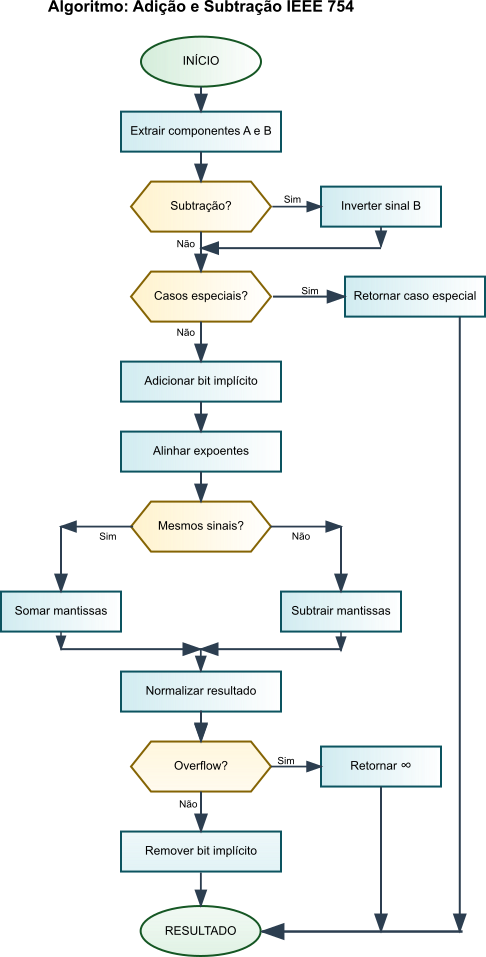 Figura 6: Fluxograma de Adição e Subtração IEEE 754
Figura 6: Fluxograma de Adição e Subtração IEEE 754
FUNÇÃO ieee754_add_sub(A, B, operação):
// Etapa 1: Casos especiais
SE A é NaN OU B é NaN:
RETORNA NaN
SE A é infinito OU B é infinito:
RETORNA tratamento_infinitos(A, B, operação)
SE A é zero:
RETORNA B (ou -B se subtração)
SE B é zero:
RETORNA A
// Etapa 2: Extração de componentes
sinal_A, exp_A, mant_A = extrair_componentes(A)
sinal_B, exp_B, mant_B = extrair_componentes(B)
// Adiciona bit implícito
mant_A = 1.mant_A
mant_B = 1.mant_B
// Etapa 3: Alinhamento
SE exp_A < exp_B:
TROCAR(A, B) // Garante que A tem maior expoente
shift = exp_A - exp_B
guard, round, sticky = deslocar_direita(mant_B, shift)
// Etapa 4: Operação
SE (sinal_A XOR sinal_B XOR (operação == SUB)):
resultado_mant = mant_A - mant_B
sinal_resultado = sinal_A
SENÃO:
resultado_mant = mant_A + mant_B
sinal_resultado = sinal_A
// Etapa 5: Normalização
SE resultado_mant >= 2.0:
sticky = sticky OR round
round = resultado_mant[0]
resultado_mant >>= 1
exp_A++
SENÃO SE resultado_mant < 1.0:
ENQUANTO resultado_mant < 1.0 E exp_A > 0:
resultado_mant <<= 1
exp_A--
// Etapa 6: Arredondamento
resultado_final = arredondar(sinal_resultado, exp_A, resultado_mant,
guard, round, sticky)
RETORNA resultado_final
Implementação em C++20
#include <iostream>
#include <bitset>
#include <cmath>
#include <iomanip>
class IEEE754Calculator {
private:
// Constantes para precisão simples (32 bits)
static constexpr uint32_t SIGN_MASK = 0x80000000;
static constexpr uint32_t EXPONENT_MASK = 0x7F800000;
static constexpr uint32_t MANTISSA_MASK = 0x007FFFFF;
static constexpr int EXPONENT_BIAS = 127;
static constexpr int MANTISSA_BITS = 23;
static constexpr int EXPONENT_BITS = 8;
struct FloatComponents {
bool sign;
int32_t exponent;
uint64_t mantissa; // 64 bits para suportar deslocamentos
bool is_nan;
bool is_infinity;
bool is_zero;
bool is_denormal;
};
// União para manipulação de bits do float
// Viu? Eu disse que union era útil!
// Esta união permite acessar o valor float como um inteiro de 32 bits
union FloatUnion {
float f;
uint32_t i;
};
static FloatComponents extract_components(float value) {
FloatUnion fu;
fu.f = value;
FloatComponents comp;
comp.sign = (fu.i & SIGN_MASK) != 0;
comp.exponent = ((fu.i & EXPONENT_MASK) >> MANTISSA_BITS);
comp.mantissa = fu.i & MANTISSA_MASK;
comp.is_nan = (comp.exponent == 0xFF) && (comp.mantissa != 0);
comp.is_infinity = (comp.exponent == 0xFF) && (comp.mantissa == 0);
comp.is_zero = (comp.exponent == 0) && (comp.mantissa == 0);
comp.is_denormal = (comp.exponent == 0) && (comp.mantissa != 0);
return comp;
}
static float construct_float(bool sign, int32_t exponent, uint64_t mantissa) {
FloatUnion fu;
// Trata números denormalizados e casos especiais
if (exponent <= 0) {
if (mantissa == 0) {
return sign ? -0.0f : 0.0f;
}
// Para denormalizados, expoente é armazenado como 0
fu.i = (sign ? SIGN_MASK : 0) | (mantissa & MANTISSA_MASK);
} else if (exponent >= 0xFF) {
// Overflow para infinito
fu.i = (sign ? SIGN_MASK : 0) | EXPONENT_MASK;
} else {
fu.i = (sign ? SIGN_MASK : 0) |
((exponent & 0xFF) << MANTISSA_BITS) |
(mantissa & MANTISSA_MASK);
}
return fu.f;
}
// Desloca mantissa para direita preservando bits R (round), G (guard) e S (sticky)
// Nomenclatura IEEE 754: R = primeiro bit perdido, G = segundo bit perdido, S = OR dos demais
static std::tuple<uint64_t, bool, bool, bool>
shift_right_with_guard_bits(uint64_t mantissa, int shift) {
bool guard = false, round = false, sticky = false;
if (shift <= 0) {
return {mantissa, guard, round, sticky};
}
if (shift >= 64) {
sticky = mantissa != 0;
return {0, false, false, sticky};
}
// Round bit (R): primeiro bit perdido - determina arredondamento
if (shift >= 1) {
round = (mantissa >> (shift - 1)) & 1;
}
// Guard bit (G): segundo bit perdido - critério adicional
if (shift >= 2) {
guard = (mantissa >> (shift - 2)) & 1;
}
// Sticky bit (S): OR de todos os outros bits perdidos
if (shift >= 3) {
uint64_t sticky_mask = (1ULL << (shift - 2)) - 1;
sticky = (mantissa & sticky_mask) != 0;
}
mantissa >>= shift;
return {mantissa, guard, round, sticky};
}
public:
static float add_subtract(float a, float b, bool is_subtraction = false) {
// Etapa 1: Tratamento de casos especiais
if (std::isnan(a) || std::isnan(b)) {
return std::numeric_limits<float>::quiet_NaN();
}
if (std::isinf(a) || std::isinf(b)) {
if (std::isinf(a) && std::isinf(b)) {
bool same_sign = (std::signbit(a) == std::signbit(b)) != is_subtraction;
if (!same_sign) {
return std::numeric_limits<float>::quiet_NaN();
}
}
return std::isinf(a) ? a : (is_subtraction ? -b : b);
}
if (a == 0.0f) return is_subtraction ? -b : b;
if (b == 0.0f) return a;
// Etapa 2: Extração de componentes
FloatComponents comp_a = extract_components(a);
FloatComponents comp_b = extract_components(b);
// Ajusta sinal para subtração
if (is_subtraction) {
comp_b.sign = !comp_b.sign;
}
// Garante que A tem o maior expoente para alinhamento
if (comp_a.exponent < comp_b.exponent) {
std::swap(comp_a, comp_b);
}
// Etapa 3: Alinhamento de expoentes
int shift = comp_a.exponent - comp_b.exponent;
// Adiciona bit implícito (exceto para números denormalizados)
uint64_t mant_a = comp_a.mantissa;
uint64_t mant_b = comp_b.mantissa;
if (!comp_a.is_denormal && comp_a.exponent != 0) {
mant_a |= (1ULL << MANTISSA_BITS);
}
if (!comp_b.is_denormal && comp_b.exponent != 0) {
mant_b |= (1ULL << MANTISSA_BITS);
}
// Desloca mantissa menor para alinhamento
auto [aligned_mant_b, guard, round, sticky] =
shift_right_with_guard_bits(mant_b, shift);
// Etapa 4: Operação aritmética
bool result_sign;
uint64_t result_mantissa;
int32_t result_exponent = comp_a.exponent;
// Declara variáveis para bits extras normalizados
bool norm_guard = guard;
bool norm_round = round;
bool norm_sticky = sticky;
if (comp_a.sign == comp_b.sign) {
// Adição efetiva
result_mantissa = mant_a + aligned_mant_b;
result_sign = comp_a.sign;
} else {
// Subtração efetiva
if (mant_a > aligned_mant_b) {
result_mantissa = mant_a - aligned_mant_b;
result_sign = comp_a.sign;
} else if (mant_a < aligned_mant_b) {
result_mantissa = aligned_mant_b - mant_a;
result_sign = comp_b.sign;
// Bits extras são zerados pois o maior estava alinhado
norm_guard = norm_round = norm_sticky = false;
} else {
// mant_a == aligned_mant_b: resultado depende dos bits extras
if (norm_round || norm_guard || norm_sticky) {
// Há resto da subtração nos bits extras
result_mantissa = 0;
result_exponent = comp_a.exponent;
result_sign = comp_a.sign;
// Mantém os bits extras para normalização
} else {
// Subtração exata resulta em zero
return 0.0f; // IEEE 754: +0.0
}
}
}
// Etapa 5: Normalização
if (result_mantissa >= (2ULL << MANTISSA_BITS)) {
// Overflow da mantissa - desloca direita
auto [new_mantissa, g, r, s] = shift_right_with_guard_bits(result_mantissa, 1);
result_mantissa = new_mantissa;
norm_guard = g;
norm_round = r;
norm_sticky = s || norm_sticky;
result_exponent++;
} else if (result_mantissa < (1ULL << MANTISSA_BITS) && result_mantissa != 0) {
// Underflow da mantissa - normalização à esquerda
while (result_mantissa < (1ULL << MANTISSA_BITS) && result_exponent > 0) {
result_mantissa <<= 1;
// Durante shift à esquerda, guard vira round, round vira LSB da mantissa
bool new_round = norm_guard;
norm_guard = false;
norm_round = new_round;
result_exponent--;
}
} else if (result_mantissa == 0) {
// Casos especiais onde only bits extras têm valores
if (norm_round || norm_guard || norm_sticky) {
// Cria número denormalizado mínimo
result_mantissa = 1;
result_exponent = 0;
norm_guard = norm_round = norm_sticky = false;
}
}
// Verifica overflow do expoente
if (result_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
// Verifica underflow para números denormalizados
if (result_exponent <= 0 && result_mantissa != 0) {
// Converte para representação denormalizada
int shift_needed = 1 - result_exponent;
auto [new_mantissa, g, r, s] = shift_right_with_guard_bits(result_mantissa, shift_needed);
result_mantissa = new_mantissa;
norm_guard = g;
norm_round = r;
norm_sticky = s || norm_sticky;
result_exponent = 0;
}
// Etapa 6: Arredondamento (round to nearest, ties to even)
// Fórmula IEEE 754: round_up = R && (S || G || LSB)
bool round_up = norm_round && (norm_sticky || norm_guard || (result_mantissa & 1));
if (round_up) {
result_mantissa++;
// Verifica overflow após arredondamento
if (result_exponent > 0 && result_mantissa >= (2ULL << MANTISSA_BITS)) {
result_mantissa >>= 1;
result_exponent++;
// Re-verifica overflow do expoente
if (result_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
} else if (result_exponent == 0 && result_mantissa >= (1ULL << MANTISSA_BITS)) {
// Transição de denormalizado para normalizado
result_mantissa &= MANTISSA_MASK;
result_exponent = 1;
}
}
// Verifica underflow total após arredondamento
if (result_mantissa == 0) {
return result_sign ? -0.0f : 0.0f;
}
// Remove bit implícito (exceto para denormalizados)
if (result_exponent > 0) {
result_mantissa &= MANTISSA_MASK;
}
return construct_float(result_sign, result_exponent, result_mantissa);
}
// Funções auxiliares para demonstração
static void print_float_details(float value, const std::string& label) {
FloatUnion fu;
fu.f = value;
std::cout << label << ": " << std::scientific << std::setprecision(6) << value << "\n";
std::cout << " Binário: " << std::bitset<32>(fu.i) << "\n";
std::cout << " Sinal: " << ((fu.i & SIGN_MASK) ? 1 : 0) << "\n";
std::cout << " Expoente: " << std::bitset<8>((fu.i & EXPONENT_MASK) >> MANTISSA_BITS)
<< " (" << (((fu.i & EXPONENT_MASK) >> MANTISSA_BITS) - EXPONENT_BIAS) << ")" << "\n";
std::cout << " Mantissa: " << std::bitset<23>(fu.i & MANTISSA_MASK) << "\n";
std::cout << "\n";
}
// Função auxiliar para demonstrar bits R, G, S
static void demonstrate_rounding_bits() {
std::cout << "=== Demonstração dos Bits R, G, S ===" << "\n";
uint64_t test_mantissa = 0b11010110111; // Exemplo
std::cout << "Mantissa original: " << std::bitset<11>(test_mantissa) << "\n";
for (int shift = 1; shift <= 5; shift++) {
auto [result, g, r, s] = shift_right_with_guard_bits(test_mantissa, shift);
std::cout << "Shift " << shift << ": "
<< std::bitset<11>(result) << " | R=" << r << " G=" << g << " S=" << s << "\n";
}
std::cout << "\n";
}
// Função para testar casos específicos de arredondamento
static void test_rounding_cases() {
std::cout << "=== Teste de Casos de Arredondamento ===" << "\n";
// Caso 1: Round bit = 0 (não arredonda)
std::cout << "Caso 1: R=0 (não arredonda)" << "\n";
float test1a = 1.25f;
float test1b = std::ldexp(1.0f, -25); // Muito pequeno
float result1 = add_subtract(test1a, test1b, false);
std::cout << test1a << " + " << test1b << " = " << result1 << "\n";
std::cout << "Esperado: não arredondar" << "\n" << "\n";
// Caso 2: R=1, S=1 (sempre arredonda)
std::cout << "Caso 2: R=1, S=1 (sempre arredonda)" << "\n";
float test2a = 1.0f + std::ldexp(1.0f, -23) + std::ldexp(1.0f, -24); // 1 + ULP + ULP/2
float test2b = std::ldexp(1.0f, -26);
float result2 = add_subtract(test2a, test2b, false);
std::cout << test2a << " + " << test2b << " = " << result2 << "\n";
std::cout << "Esperado: arredondar para cima" << "\n" << "\n";
// Caso 3: R=1, S=0, LSB=0 (ties to even - não arredonda)
std::cout << "Caso 3: R=1, S=0, LSB=0 (ties to even - não arredonda)" << "\n";
float test3a = 1.0f + std::ldexp(1.0f, -23); // 1 + ULP (LSB=0)
float test3b = std::ldexp(1.0f, -25); // Exatamente ULP/4
float result3 = add_subtract(test3a, test3b, false);
std::cout << test3a << " + " << test3b << " = " << result3 << "\n";
std::cout << "Esperado: não arredondar (ties to even)" << "\n" << "\n";
// Caso 4: R=1, S=0, LSB=1 (ties to even - arredonda)
std::cout << "Caso 4: R=1, S=0, LSB=1 (ties to even - arredonda)" << "\n";
float test4a = 1.0f + 3.0f * std::ldexp(1.0f, -23); // 1 + 3*ULP (LSB=1)
float test4b = std::ldexp(1.0f, -25); // Exatamente ULP/4
float result4 = add_subtract(test4a, test4b, false);
std::cout << test4a << " + " << test4b << " = " << result4 << "\n";
std::cout << "Esperado: arredondar para cima (ties to even)" << "\n" << "\n";
}
};
int main() {
std::cout << "=== Implementação da Soma em `IEEE 754` ===" << "\n" << "\n";
// Demonstração dos bits de arredondamento
IEEE754Calculator::demonstrate_rounding_bits();
// Testes de arredondamento específicos
IEEE754Calculator::test_rounding_cases();
// Exemplo 1: Adição simples
float a = 3.25f;
float b = 1.75f;
std::cout << "EXEMPLO 1: Adição com expoentes diferentes" << "\n";
IEEE754Calculator::print_float_details(a, "Operando A");
IEEE754Calculator::print_float_details(b, "Operando B");
float result_add = IEEE754Calculator::add_subtract(a, b, false);
float expected_add = a + b;
IEEE754Calculator::print_float_details(result_add, "Resultado (implementação)");
IEEE754Calculator::print_float_details(expected_add, "Resultado (FPU)");
std::cout << "Resultados idênticos: " << (result_add == expected_add ? "Sim" : "Não") << "\n";
std::cout << std::string(50, '-') << "\n" << "\n";
// Exemplo 2: Subtração com cancelamento catastrófico
float c = 1.0000001f;
float d = 1.0f;
std::cout << "EXEMPLO 2: Subtração com cancelamento catastrófico" << "\n";
IEEE754Calculator::print_float_details(c, "Operando C");
IEEE754Calculator::print_float_details(d, "Operando D");
float result_sub = IEEE754Calculator::add_subtract(c, d, true);
float expected_sub = c - d;
IEEE754Calculator::print_float_details(result_sub, "Resultado (implementação)");
IEEE754Calculator::print_float_details(expected_sub, "Resultado (FPU)");
std::cout << "Resultados idênticos: " << (result_sub == expected_sub ? "Sim" : "Não") << "\n";
std::cout << std::string(50, '-') << "\n" << "\n";
// Exemplo 3: Casos especiais (infinito)
std::cout << "EXEMPLO 3: Casos especiais (infinito)" << "\n";
float inf = std::numeric_limits<float>::infinity();
float nan_result = IEEE754Calculator::add_subtract(inf, -inf, false);
std::cout << "∞ + (-∞) = " << nan_result << " (NaN esperado)" << "\n";
std::cout << "É NaN: " << (std::isnan(nan_result) ? "Sim" : "Não") << "\n";
std::cout << std::string(50, '-') << "\n" << "\n";
// Exemplo 4: Adição de números denormalizados
std::cout << "EXEMPLO 4: Adição de números denormalizados" << "\n";
float denorm1 = std::nextafter(0.0f, 1.0f);
float denorm2 = denorm1;
IEEE754Calculator::print_float_details(denorm1, "Operando Denorm1");
IEEE754Calculator::print_float_details(denorm2, "Operando Denorm2");
float result_denorm = IEEE754Calculator::add_subtract(denorm1, denorm2, false);
float expected_denorm = denorm1 + denorm2;
IEEE754Calculator::print_float_details(result_denorm, "Resultado (implementação)");
IEEE754Calculator::print_float_details(expected_denorm, "Resultado (FPU)");
std::cout << "Resultados idênticos: " << (result_denorm == expected_denorm ? "Sim" : "Não") << "\n";
std::cout << std::string(50, '-') << "\n" << "\n";
// Exemplo 5: Overflow extremo
std::cout << "EXEMPLO 5: Overflow extremo" << "\n";
float max_float = std::numeric_limits<float>::max();
float large = max_float / 2.0f;
IEEE754Calculator::print_float_details(max_float, "Operando MaxFloat");
IEEE754Calculator::print_float_details(large, "Operando Large");
float result_overflow = IEEE754Calculator::add_subtract(max_float, large, false);
float expected_overflow = max_float + large;
IEEE754Calculator::print_float_details(result_overflow, "Resultado (implementação)");
IEEE754Calculator::print_float_details(expected_overflow, "Resultado (FPU)");
std::cout << "Resultados idênticos: " << (std::isinf(result_overflow) && std::isinf(expected_overflow) ? "Sim" : "Não") << "\n";
std::cout << "\n" << "=== Fim do Teste ===" << "\n";
return 0;
}
Implementação da Multiplicação de Ponto Flutuante IEEE 754
A multiplicação de números de ponto flutuante IEEE 754 segue uma abordagem fundamentalmente diferente da adição e subtração. Enquanto as operações aditivas requerem alinhamento de expoentes e podem resultar em cancelamento catastrófico, a multiplicação trabalha com a propriedade matemática fundamental: $(M_1 \times 2^{E_1}) \times (M_2 \times 2^{E_2}) = (M_1 \times M_2) \times 2^{E_1 + E_2}$.
A multiplicação de dois números IEEE 754 pode ser expressa como:
Na qual:
- $s_1, s_2$: bits de sinal dos operandos;
- $M_1, M_2$: significandos (mantissas) normalizados, tipicamente $1.xxx \times 2^0$;
- $E_1, E_2$: expoentes sem enviesamento;
- $\oplus$: operação XOR para determinação do sinal do resultado.
Esta formulação destaca as três operações fundamentais da multiplicação IEEE 754:
- Determinação do sinal: $s_{resultado} = s_1 \oplus s_2$;
- Adição de expoentes: $E_{resultado} = E_1 + E_2$;
- Multiplicação de significandos: $M_{resultado} = M_1 \times M_2$.
O algoritmo de multiplicação IEEE 754 é organizado em seis etapas principais, cada uma tratando aspectos específicos da representação de ponto flutuante:
1. Tratamento de Casos Especiais
Antes de realizar qualquer operação aritmética, o algoritmo verifica e trata valores excepcionais conforme as especificações IEEE 754:
- Propagação de
NaN: qualquer operandoNaNresulta emNaN; - Multiplicação por zero: zero multiplicado por qualquer número finito resulta em zero;
- Multiplicação por infinito: infinito multiplicado por número finito não-zero resulta em infinito;
- Casos indeterminados: $0 \times \infty$ resulta em
NaN.
2. Extração de Componentes e Determinação do Sinal
Para operandos finitos não-zero, extraímos os componentes individuais e determinamos o sinal do resultado:
\[s_{resultado} = s_1 \oplus s_2\]O sinal do produto é positivo se ambos operandos têm o mesmo sinal, e negativo caso contrário.
3. Adição de Expoentes
Os expoentes dos operandos são somados após remoção do enviesamento:
\[E_{resultado} = (E_1 - \text{bias}) + (E_2 - \text{bias}) + \text{bias} = E_1 + E_2 - \text{bias}\]Para precisão simples, $\text{bias} = 127$; para precisão dupla, $\text{bias} = 1023$.
4. Multiplicação de Significandos
Esta é a etapa computacionalmente mais intensiva. Os significandos são tratados como números inteiros fixos com bit implícito:
- Precisão simples: significandos de $24$ bits, $23$ explícitos $+ 1$ implícito;
- Multiplicação completa: produz resultado de até $48$ bits;
- Preservação de precisão: bits extras são mantidos para arredondamento.
A multiplicação de dois números da forma $1.M_1 \times 1.M_2$ resulta em um valor no intervalo $[1.0, 4.0)$, exigindo normalização posterior.
5. Normalização
Assim como ocorre com adição, o produto dos significandos pode exigir normalização:
Caso 1: Produto $\geq 2.0$
- Desloca o resultado 1 bit à direita;
- Incrementa o expoente em 1;
- Preserva bits extras para arredondamento.
Caso 2: Produto $< 2.0$ (já normalizado)
- Mantém o resultado como está;
- Nenhum ajuste de expoente necessário.
6. Arredondamento
Aplica-se o modo de arredondamento IEEE 754 usando os bits extras preservados durante a multiplicação e normalização. O modo padrão roundTiesToEven utiliza a mesma lógica de guard, round e sticky bits apresentada na implementação da adição.
Considerações Especiais da Multiplicação
A multiplicação de ponto flutuante IEEE 754 também deve considerar casos de overflow e underflow, à saber:
- Overflow de Expoente: quando $E_1 + E_2 - \text{bias} \geq E_{\max}$, o resultado satura para infinito;
- Underflow de Expoente: quando $E_1 + E_2 - \text{bias} \leq 0$, pode resultar em números denormalizados ou zero;
- Números Denormalizados: operandos denormalizados requerem tratamento especial, pois não possuem bit implícito.
Pseudocódigo e Fluxograma da Multiplicação
 Figura 7: Fluxograma da multiplicação segundo a norma IEEE 754
Figura 7: Fluxograma da multiplicação segundo a norma IEEE 754
multiplication_flowchart.webp
FUNÇÃO ieee754_multiply(A, B):
// Etapa 1: Casos especiais
SE A é NaN OU B é NaN:
RETORNA NaN
SE A é infinito OU B é infinito:
SE A é zero OU B é zero:
RETORNA NaN // 0 × ∞
SENÃO:
RETORNA sinal_resultado × infinito
SE A é zero OU B é zero:
RETORNA sinal_resultado × zero
// Etapa 2: Extração e sinal
sinal_A, exp_A, mant_A = extrair_componentes(A)
sinal_B, exp_B, mant_B = extrair_componentes(B)
sinal_resultado = sinal_A XOR sinal_B
// Adiciona bit implícito (se não denormalizado)
SE NOT denormalizado(A): mant_A |= (1 << 23)
SE NOT denormalizado(B): mant_B |= (1 << 23)
// Etapa 3: Adição de expoentes
exp_resultado = exp_A + exp_B - BIAS
// Etapa 4: Multiplicação de significandos
produto_completo = mant_A × mant_B
// Etapa 5: Normalização
SE produto_completo >= (2^47): // Para precisão simples
guard, round, sticky = extrair_bits_extras(produto_completo, 1)
produto_completo >>= 1
exp_resultado += 1
SENÃO:
guard, round, sticky = extrair_bits_extras(produto_completo, 0)
// Etapa 6: Verificação de overflow/underflow
SE exp_resultado >= 255: // Overflow
RETORNA sinal_resultado × infinito
SE exp_resultado <= 0: // Underflow/denormalizado
// Tratamento especial para denormalizados
// Etapa 7: Arredondamento
resultado_final = arredondar(sinal_resultado, exp_resultado,
produto_completo, guard, round, sticky)
RETORNA resultado_final
Implementação em C++20: Melhorando a classe IEEE754Calculator
Expandindo a classe existente para incluir multiplicação, mantemos toda a funcionalidade de adição e subtração enquanto adicionamos os novos métodos necessários:
#include <iostream>
#include <bitset>
#include <cmath>
#include <iomanip>
class IEEE754Calculator {
private:
// ===== CONSTANTES EXISTENTES (mantidas) =====
static constexpr uint32_t SIGN_MASK = 0x80000000;
static constexpr uint32_t EXPONENT_MASK = 0x7F800000;
static constexpr uint32_t MANTISSA_MASK = 0x007FFFFF;
static constexpr int EXPONENT_BIAS = 127;
static constexpr int MANTISSA_BITS = 23;
static constexpr int EXPONENT_BITS = 8;
// ===== ESTRUTURAS EXISTENTES (mantidas) =====
struct FloatComponents {
bool sign;
int32_t exponent;
uint64_t mantissa;
bool is_nan;
bool is_infinity;
bool is_zero;
bool is_denormal;
};
union FloatUnion {
float f;
uint32_t i;
};
static FloatComponents extract_components(float value) {
FloatUnion fu;
fu.f = value;
FloatComponents comp;
comp.sign = (fu.i & SIGN_MASK) != 0;
comp.exponent = ((fu.i & EXPONENT_MASK) >> MANTISSA_BITS);
comp.mantissa = fu.i & MANTISSA_MASK;
comp.is_nan = (comp.exponent == 0xFF) && (comp.mantissa != 0);
comp.is_infinity = (comp.exponent == 0xFF) && (comp.mantissa == 0);
comp.is_zero = (comp.exponent == 0) && (comp.mantissa == 0);
comp.is_denormal = (comp.exponent == 0) && (comp.mantissa != 0);
return comp;
}
static float construct_float(bool sign, int32_t exponent, uint64_t mantissa) {
FloatUnion fu;
if (exponent <= 0) {
if (mantissa == 0) {
return sign ? -0.0f : 0.0f;
}
fu.i = (sign ? SIGN_MASK : 0) | (mantissa & MANTISSA_MASK);
} else if (exponent >= 0xFF) {
fu.i = (sign ? SIGN_MASK : 0) | EXPONENT_MASK;
} else {
fu.i = (sign ? SIGN_MASK : 0) |
((exponent & 0xFF) << MANTISSA_BITS) |
(mantissa & MANTISSA_MASK);
}
return fu.f;
}
static std::tuple<uint64_t, bool, bool, bool>
shift_right_with_guard_bits(uint64_t mantissa, int shift) {
bool guard = false, round = false, sticky = false;
if (shift <= 0) {
return {mantissa, guard, round, sticky};
}
if (shift >= 64) {
sticky = mantissa != 0;
return {0, false, false, sticky};
}
if (shift >= 1) {
round = (mantissa >> (shift - 1)) & 1;
}
if (shift >= 2) {
guard = (mantissa >> (shift - 2)) & 1;
}
if (shift >= 3) {
uint64_t sticky_mask = (1ULL << (shift - 2)) - 1;
sticky = (mantissa & sticky_mask) != 0;
}
mantissa >>= shift;
return {mantissa, guard, round, sticky};
}
// ===== NOVOS MÉTODOS PARA MULTIPLICAÇÃO =====
// Extrai bits de guarda após multiplicação de significandos
static std::tuple<bool, bool, bool> extract_guard_bits_from_product(
uint64_t product, int effective_shift) {
bool guard = false, round = false, sticky = false;
// Para multiplicação, o produto tem até 48 bits (24×24)
// Precisamos extrair para manter 24 bits no resultado
int total_shift = 24 + effective_shift;
if (total_shift >= 1) {
round = (product >> (total_shift - 1)) & 1;
}
if (total_shift >= 2) {
guard = (product >> (total_shift - 2)) & 1;
}
if (total_shift >= 3) {
uint64_t mask = (1ULL << (total_shift - 2)) - 1;
sticky = (product & mask) != 0;
}
return {guard, round, sticky};
}
// Multiplica dois significandos de 24 bits
static uint64_t multiply_significands(uint64_t mant_a, uint64_t mant_b) {
// Multiplicação completa preservando toda a precisão
return mant_a * mant_b;
}
// Normaliza produto da multiplicação
static std::tuple<uint64_t, int32_t, bool, bool, bool>
normalize_multiplication_result(uint64_t product, int32_t exponent) {
bool guard, round, sticky;
// O produto de dois números 1.xxx pode estar no intervalo [1.0, 4.0)
// Se >= 2.0, precisa deslocar 1 bit à direita
if (product >= (1ULL << 47)) { // >= 2^47 para produto de 24×24 bits
auto [g, r, s] = extract_guard_bits_from_product(product, 1);
guard = g; round = r; sticky = s;
product >>= 1;
exponent += 1;
} else {
auto [g, r, s] = extract_guard_bits_from_product(product, 0);
guard = g; round = r; sticky = s;
}
// Ajusta para manter apenas os 24 bits mais significativos
product >>= 24;
return {product, exponent, guard, round, sticky};
}
public:
static float add_subtract(float a, float b, bool is_subtraction = false) {
// [Todo o código da implementação anterior mantido exatamente igual]
// ... só removi os comentários para manter o foco na nova funcionalidade
if (std::isnan(a) || std::isnan(b)) {
return std::numeric_limits<float>::quiet_NaN();
}
if (std::isinf(a) || std::isinf(b)) {
if (std::isinf(a) && std::isinf(b)) {
bool same_sign = (std::signbit(a) == std::signbit(b)) != is_subtraction;
if (!same_sign) {
return std::numeric_limits<float>::quiet_NaN();
}
}
return std::isinf(a) ? a : (is_subtraction ? -b : b);
}
if (a == 0.0f) return is_subtraction ? -b : b;
if (b == 0.0f) return a;
FloatComponents comp_a = extract_components(a);
FloatComponents comp_b = extract_components(b);
if (is_subtraction) {
comp_b.sign = !comp_b.sign;
}
if (comp_a.exponent < comp_b.exponent) {
std::swap(comp_a, comp_b);
}
int shift = comp_a.exponent - comp_b.exponent;
uint64_t mant_a = comp_a.mantissa;
uint64_t mant_b = comp_b.mantissa;
if (!comp_a.is_denormal && comp_a.exponent != 0) {
mant_a |= (1ULL << MANTISSA_BITS);
}
if (!comp_b.is_denormal && comp_b.exponent != 0) {
mant_b |= (1ULL << MANTISSA_BITS);
}
auto [aligned_mant_b, guard, round, sticky] =
shift_right_with_guard_bits(mant_b, shift);
bool result_sign;
uint64_t result_mantissa;
int32_t result_exponent = comp_a.exponent;
bool norm_guard = guard;
bool norm_round = round;
bool norm_sticky = sticky;
if (comp_a.sign == comp_b.sign) {
result_mantissa = mant_a + aligned_mant_b;
result_sign = comp_a.sign;
} else {
if (mant_a > aligned_mant_b) {
result_mantissa = mant_a - aligned_mant_b;
result_sign = comp_a.sign;
} else if (mant_a < aligned_mant_b) {
result_mantissa = aligned_mant_b - mant_a;
result_sign = comp_b.sign;
norm_guard = norm_round = norm_sticky = false;
} else {
if (norm_round || norm_guard || norm_sticky) {
result_mantissa = 0;
result_exponent = comp_a.exponent;
result_sign = comp_a.sign;
} else {
return 0.0f;
}
}
}
if (result_mantissa >= (2ULL << MANTISSA_BITS)) {
auto [new_mantissa, g, r, s] = shift_right_with_guard_bits(result_mantissa, 1);
result_mantissa = new_mantissa;
norm_guard = g;
norm_round = r;
norm_sticky = s || norm_sticky;
result_exponent++;
} else if (result_mantissa < (1ULL << MANTISSA_BITS) && result_mantissa != 0) {
while (result_mantissa < (1ULL << MANTISSA_BITS) && result_exponent > 0) {
result_mantissa <<= 1;
bool new_round = norm_guard;
norm_guard = false;
norm_round = new_round;
result_exponent--;
}
} else if (result_mantissa == 0) {
if (norm_round || norm_guard || norm_sticky) {
result_mantissa = 1;
result_exponent = 0;
norm_guard = norm_round = norm_sticky = false;
}
}
if (result_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
if (result_exponent <= 0 && result_mantissa != 0) {
int shift_needed = 1 - result_exponent;
auto [new_mantissa, g, r, s] = shift_right_with_guard_bits(result_mantissa, shift_needed);
result_mantissa = new_mantissa;
norm_guard = g;
norm_round = r;
norm_sticky = s || norm_sticky;
result_exponent = 0;
}
bool round_up = norm_round && (norm_sticky || norm_guard || (result_mantissa & 1));
if (round_up) {
result_mantissa++;
if (result_exponent > 0 && result_mantissa >= (2ULL << MANTISSA_BITS)) {
result_mantissa >>= 1;
result_exponent++;
if (result_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
} else if (result_exponent == 0 && result_mantissa >= (1ULL << MANTISSA_BITS)) {
result_mantissa &= MANTISSA_MASK;
result_exponent = 1;
}
}
if (result_mantissa == 0) {
return result_sign ? -0.0f : 0.0f;
}
if (result_exponent > 0) {
result_mantissa &= MANTISSA_MASK;
}
return construct_float(result_sign, result_exponent, result_mantissa);
}
static float multiply(float a, float b) {
// Etapa 1: Tratamento de casos especiais
if (std::isnan(a) || std::isnan(b)) {
return std::numeric_limits<float>::quiet_NaN();
}
// Casos especiais com infinito
if (std::isinf(a) || std::isinf(b)) {
// Verifica casos indeterminados: 0 × ∞
if ((a == 0.0f && std::isinf(b)) || (b == 0.0f && std::isinf(a))) {
return std::numeric_limits<float>::quiet_NaN();
}
// Infinito × número finito não-zero = infinito com sinal correto
bool result_sign = std::signbit(a) ^ std::signbit(b);
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
// Multiplicação por zero
if (a == 0.0f || b == 0.0f) {
bool result_sign = std::signbit(a) ^ std::signbit(b);
return result_sign ? -0.0f : 0.0f;
}
// Etapa 2: Extração de componentes
FloatComponents comp_a = extract_components(a);
FloatComponents comp_b = extract_components(b);
// Determinação do sinal: XOR dos bits de sinal
bool result_sign = comp_a.sign ^ comp_b.sign;
// Etapa 3: Preparação dos significandos
uint64_t mant_a = comp_a.mantissa;
uint64_t mant_b = comp_b.mantissa;
// Adiciona bit implícito para números normalizados
if (!comp_a.is_denormal) {
mant_a |= (1ULL << MANTISSA_BITS);
}
if (!comp_b.is_denormal) {
mant_b |= (1ULL << MANTISSA_BITS);
}
// Etapa 4: Cálculo do expoente resultante
int32_t result_exponent;
if (comp_a.is_denormal || comp_b.is_denormal) {
// Tratamento especial para números denormalizados
result_exponent = comp_a.exponent + comp_b.exponent - EXPONENT_BIAS + 1;
} else {
result_exponent = comp_a.exponent + comp_b.exponent - EXPONENT_BIAS;
}
// Etapa 5: Multiplicação dos significandos
uint64_t product = multiply_significands(mant_a, mant_b);
// Etapa 6: Normalização
auto [normalized_mantissa, final_exponent, guard, round, sticky] =
normalize_multiplication_result(product, result_exponent);
// Etapa 7: Verificação de overflow/underflow
if (final_exponent >= 0xFF) {
// Overflow - retorna infinito
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
if (final_exponent <= 0) {
// Underflow - pode resultar em número denormalizado ou zero
if (final_exponent < -23) {
// Underflow total - resultado é zero
return result_sign ? -0.0f : 0.0f;
}
// Conversão para número denormalizado
int shift_needed = 1 - final_exponent;
auto [denorm_mantissa, g, r, s] =
shift_right_with_guard_bits(normalized_mantissa, shift_needed);
normalized_mantissa = denorm_mantissa;
guard = g;
round = r;
sticky = s || sticky;
final_exponent = 0;
}
// Etapa 8: Arredondamento (round to nearest, ties to even)
bool round_up = round && (sticky || guard || (normalized_mantissa & 1));
if (round_up) {
normalized_mantissa++;
// Verifica overflow após arredondamento
if (final_exponent > 0 && normalized_mantissa >= (2ULL << MANTISSA_BITS)) {
normalized_mantissa >>= 1;
final_exponent++;
// Re-verifica overflow
if (final_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
} else if (final_exponent == 0 && normalized_mantissa >= (1ULL << MANTISSA_BITS)) {
// Transição de denormalizado para normalizado
normalized_mantissa &= MANTISSA_MASK;
final_exponent = 1;
}
}
// Remove bit implícito para números normalizados
if (final_exponent > 0) {
normalized_mantissa &= MANTISSA_MASK;
}
return construct_float(result_sign, final_exponent, normalized_mantissa);
}
static void print_float_details(float value, const std::string& label) {
FloatUnion fu;
fu.f = value;
std::cout << label << ": " << std::scientific << std::setprecision(6) << value << "\n";
std::cout << " Binário: " << std::bitset<32>(fu.i) << "\n";
std::cout << " Sinal: " << ((fu.i & SIGN_MASK) ? 1 : 0) << "\n";
std::cout << " Expoente: " << std::bitset<8>((fu.i & EXPONENT_MASK) >> MANTISSA_BITS)
<< " (" << (((fu.i & EXPONENT_MASK) >> MANTISSA_BITS) - EXPONENT_BIAS) << ")" << "\n";
std::cout << " Mantissa: " << std::bitset<23>(fu.i & MANTISSA_MASK) << "\n";
std::cout << "\n";
}
static void demonstrate_rounding_bits() {
std::cout << "=== Demonstração dos Bits R, G, S ===" << "\n";
uint64_t test_mantissa = 0b11010110111;
std::cout << "Mantissa original: " << std::bitset<11>(test_mantissa) << "\n";
for (int shift = 1; shift <= 5; shift++) {
auto [result, g, r, s] = shift_right_with_guard_bits(test_mantissa, shift);
std::cout << "Shift " << shift << ": "
<< std::bitset<11>(result) << " | R=" << r << " G=" << g << " S=" << s << "\n";
}
std::cout << "\n";
}
// Novos métodos auxiliares para a multiplicação
static void demonstrate_multiplication_algorithm() {
std::cout << "=== Demonstração do Algoritmo de Multiplicação ===" << "\n";
// Exemplo com números que requerem normalização
float a = 1.5f; // 1.100... × 2^0
float b = 1.25f; // 1.010... × 2^0
std::cout << "Multiplicação: " << a << " × " << b << "\n";
FloatComponents comp_a = extract_components(a);
FloatComponents comp_b = extract_components(b);
std::cout << "Componentes de A: sinal=" << comp_a.sign
<< ", exp=" << (comp_a.exponent - EXPONENT_BIAS)
<< ", mant=" << std::bitset<24>(comp_a.mantissa | (1 << 23)) << "\n";
std::cout << "Componentes de B: sinal=" << comp_b.sign
<< ", exp=" << (comp_b.exponent - EXPONENT_BIAS)
<< ", mant=" << std::bitset<24>(comp_b.mantissa | (1 << 23)) << "\n";
uint64_t mant_a = comp_a.mantissa | (1ULL << MANTISSA_BITS);
uint64_t mant_b = comp_b.mantissa | (1ULL << MANTISSA_BITS);
uint64_t product = mant_a * mant_b;
std::cout << "Produto dos significandos: " << std::bitset<48>(product) << "\n";
std::cout << "Expoente resultante: " << (comp_a.exponent + comp_b.exponent - EXPONENT_BIAS) << "\n";
bool result_sign = comp_a.sign ^ comp_b.sign;
std::cout << "Sinal resultante: " << result_sign << "\n";
float our_result = multiply(a, b);
float fpu_result = a * b;
std::cout << "Resultado nossa implementação: " << our_result << "\n";
std::cout << "Resultado FPU: " << fpu_result << "\n";
std::cout << "Idênticos: " << (our_result == fpu_result ? "Sim" : "Não") << "\n\n";
}
static void test_multiplication_special_cases() {
std::cout << "=== Teste de Casos Especiais da Multiplicação ===" << "\n";
// Caso 1: Multiplicação por zero
std::cout << "Caso 1: Multiplicação por zero" << "\n";
float result1 = multiply(3.14f, 0.0f);
std::cout << "3.14 × 0.0 = " << result1 << "\n";
std::cout << "É zero: " << (result1 == 0.0f ? "Sim" : "Não") << "\n\n";
// Caso 2: Multiplicação por infinito
std::cout << "Caso 2: Multiplicação por infinito" << "\n";
float inf = std::numeric_limits<float>::infinity();
float result2 = multiply(2.0f, inf);
std::cout << "2.0 × ∞ = " << result2 << "\n";
std::cout << "É infinito: " << (std::isinf(result2) ? "Sim" : "Não") << "\n\n";
// Caso 3: Indeterminado 0 × ∞
std::cout << "Caso 3: Indeterminado 0 × ∞" << "\n";
float result3 = multiply(0.0f, inf);
std::cout << "0.0 × ∞ = " << result3 << "\n";
std::cout << "É NaN: " << (std::isnan(result3) ? "Sim" : "Não") << "\n\n";
// Caso 4: Overflow
std::cout << "Caso 4: Overflow" << "\n";
float max_val = std::numeric_limits<float>::max();
float result4 = multiply(max_val, 2.0f);
std::cout << "max_float × 2.0 = " << result4 << "\n";
std::cout << "É infinito: " << (std::isinf(result4) ? "Sim" : "Não") << "\n\n";
// Caso 5: Underflow
std::cout << "Caso 5: Underflow" << "\n";
float min_val = std::numeric_limits<float>::min();
float result5 = multiply(min_val, 0.5f);
std::cout << "min_float × 0.5 = " << result5 << "\n";
std::cout << "É denormalizado ou zero: " << (result5 != 0.0f && std::fpclassify(result5) == FP_SUBNORMAL ? "Denormalizado" : "Zero") << "\n\n";
}
static void test_rounding_in_multiplication() {
std::cout << "=== Teste de Arredondamento na Multiplicação ===" << "\n";
// Teste com números que geram bits extras significativos
float a = 1.0f + std::ldexp(1.0f, -22); // 1 + ULP/2
float b = 1.0f + std::ldexp(1.0f, -22); // 1 + ULP/2
std::cout << "Teste round to nearest, ties to even:" << "\n";
std::cout << "a = " << std::hexfloat << a << std::defaultfloat << "\n";
std::cout << "b = " << std::hexfloat << b << std::defaultfloat << "\n";
float our_result = multiply(a, b);
float fpu_result = a * b;
std::cout << "Resultado nossa implementação: " << std::hexfloat << our_result << std::defaultfloat << "\n";
std::cout << "Resultado FPU: " << std::hexfloat << fpu_result << std::defaultfloat << "\n";
std::cout << "Idênticos: " << (our_result == fpu_result ? "Sim" : "Não") << "\n\n";
}
};
int main() {
std::cout << "=== Implementação da Multiplicação IEEE 754 ===" << "\n\n";
// Testes existentes de adição mantidos
std::cout << "=== Verificação da Funcionalidade de Adição (Mantida) ===" << "\n";
float test_add_a = 3.25f;
float test_add_b = 1.75f;
float result_add = IEEE754Calculator::add_subtract(test_add_a, test_add_b, false);
float expected_add = test_add_a + test_add_b;
std::cout << test_add_a << " + " << test_add_b << " = " << result_add << "\n";
std::cout << "FPU result: " << expected_add << "\n";
std::cout << "Adição funciona: " << (result_add == expected_add ? "Sim" : "Não") << "\n\n";
// Novos testes de multiplicação
IEEE754Calculator::demonstrate_multiplication_algorithm();
IEEE754Calculator::test_multiplication_special_cases();
IEEE754Calculator::test_rounding_in_multiplication();
// Exemplo detalhado de multiplicação
std::cout << "=== Exemplo Detalhado de Multiplicação ===" << "\n";
float a = 2.5f; // 10.1 em binário
float b = 1.5f; // 1.1 em binário
IEEE754Calculator::print_float_details(a, "Operando A");
IEEE754Calculator::print_float_details(b, "Operando B");
float result = IEEE754Calculator::multiply(a, b);
float expected = a * b;
IEEE754Calculator::print_float_details(result, "Resultado (nossa implementação)");
IEEE754Calculator::print_float_details(expected, "Resultado (FPU)");
std::cout << "Resultados idênticos: " << (result == expected ? "Sim" : "Não") << "\n";
std::cout << "Valor esperado: " << expected << " (2.5 × 1.5 = 3.75)" << "\n\n";
// Teste de performance comparativa
std::cout << "=== Comparação com Operações Padrão ===" << "\n";
std::vector<std::pair<float, float>> test_cases = {
{1.0f, 1.0f},
{-2.5f, 3.7f},
{0.125f, 8.0f},
{1e20f, 1e-20f},
{std::sqrt(2.0f), std::sqrt(8.0f)}
};
bool all_match = true;
for (const auto& [x, y] : test_cases) {
float our_mult = IEEE754Calculator::multiply(x, y);
float fpu_mult = x * y;
float our_add = IEEE754Calculator::add_subtract(x, y, false);
float fpu_add = x + y;
bool mult_match = our_mult == fpu_mult;
bool add_match = our_add == fpu_add;
all_match = all_match && mult_match && add_match;
std::cout << "(" << x << ", " << y << "): "
<< "Mult " << (mult_match ? "✓" : "✗") << " "
<< "Add " << (add_match ? "✓" : "✗") << "\n";
}
std::cout << "\nTodos os testes passaram: " << (all_match ? "✓ SIM" : "✗ NÃO") << "\n";
std::cout << "\n=== Fim dos Testes ===" << "\n";
return 0;
}
Nesta implementação, mantivemos a estrutura da classe existente, preservando todos os métodos de adição e subtração. A adição de novos métodos para multiplicação foi feita de forma modular, garantindo que a funcionalidade original não fosse afetada. Porém adicionamos novos métodos específicos para lidar com a multiplicação IEEE 754, incluindo:
extract_guard_bits_from_product(): especializado para extrair bits de guarda após multiplicação de significandos de $24$ bits;multiply_significands(): realiza multiplicação completa preservando toda a precisão;normalize_multiplication_result(): normaliza especificamente produtos de multiplicação;multiply(): método principal para multiplicaçãoIEEE 754;demonstrate_multiplication_algorithm(): demonstra passo a passo o algoritmo;test_multiplication_special_cases(): testa casos especiais da multiplicação;test_rounding_in_multiplication(): verifica arredondamento específico da multiplicação;
Com esta implementação garantimos a Preservação de Precisão. Ou seja, a multiplicação mantém todos os 48 bits do produto intermediário antes do arredondamento, garantindo precisão máxima. Além disso, a implementação inclui todos os casos definidos na norma ` IEEE 754, incluindo comportamentos específicos para NaN, infinito e zero. A normalização é feita de forma otimizada, garantindo que todos os resultados estejam na forma padrão do IEEE 754. Isso quer dizer que o algoritmo apenas os casos necessários, produto $≥ 2.0$ ou $< 2.0$ enquanto preserva a precisão utilizando a mesma lógica de arredondamento roundTiesToEven já implementada para adição e subtração.
Implementação da Divisão de Ponto Flutuante IEEE 754
A divisão de números de ponto flutuante IEEE 754 representa o desafio algorítmico mais complexo entre as operações aritméticas fundamentais. A implementação deve lidar com numerosos casos especiais, mantendo a precisão por meio do cálculo iterativo do quociente. Diferentemente da multiplicação, onde o produto é calculado diretamente, a divisão requer algoritmos iterativos sofisticados para determinar cada bit do quociente com precisão.
A divisão de dois números IEEE 754 pode ser expressa como:
\[\frac{(-1)^{s_1} \times M_1 \times 2^{E_1}}{(-1)^{s_2} \times M_2 \times 2^{E_2}} = (-1)^{s_1 \oplus s_2} \times \frac{M_1}{M_2} \times 2^{E_1 - E_2}\]Na qual, temos:
- $s_1, s_2$: bits de sinal do dividendo e divisor;
- $M_1, M_2$: significandos normalizados no intervalo $[1.0, 2.0)$;
- $E_1, E_2$: expoentes sem enviesamento;
- $\oplus$: operação XOR para determinação do sinal.
Esta formulação revela as três operações fundamentais da divisão IEEE 754:
- Determinação do sinal: $s_{resultado} = s_1 \oplus s_2$;
- Subtração de expoentes: $E_{resultado} = E_1 - E_2 + \text{bias}$;
- Divisão de significandos: $Q = \frac{M_1}{M_2}$, onde $Q \in [0.5, 2.0)$.
A divisão apresenta complexidades únicas que a distinguem das demais operações:
-
Natureza Iterativa: diferentemente da adição e multiplicação, que produzem resultados exatos em uma operação, a divisão requer cálculo bit a bit do quociente por meio de algoritmos iterativos.
-
Intervalo do Quociente: para significandos normalizados $M_1, M_2 \in [1.0, 2.0)$, o quociente $\frac{M_1}{M_2}$ está no intervalo $[0.5, 2.0)$, podendo exigir normalização quando $Q < 1.0$.
-
Algoritmos de Divisão: a literatura apresenta várias abordagens, cada uma com trade-offs entre complexidade e performance:
- Algoritmo Restoring: conceptualmente simples, realiza tentativa e correção;
- Algoritmo Non-Restoring: mais eficiente, evita operações de correção;
- Algoritmo SRT: usado em processadores modernos, permite dígitos quociente ${-1, 0, 1}$;
- Métodos Newton-Raphson: convergência quadrática, usado em implementações de alta performance.
Implementaremos o algoritmo restoring devido à sua clareza conceptual e facilidade de verificação. O algoritmo é organizado em sete etapas principais:
1. Tratamento de Casos Especiais
A divisão possui o maior número de casos especiais entre as operações IEEE 754:
- Divisão por zero: $\frac{\text{finito não-zero}}{0} = \pm\infty$, $\frac{0}{0} = \text{NaN}$;
- Divisão de infinitos: $\frac{\infty}{\infty} = \text{NaN}$, $\frac{\infty}{\text{finito}} = \pm\infty$;
- Divisão de zero: $\frac{0}{\text{finito não-zero}} = \pm 0$;
- Propagação de NaN: qualquer operando
NaNresulta emNaN.
2. Extração de Componentes e Determinação do Sinal
Para operandos finitos não-zero, extraímos os componentes e determinamos o sinal:
\[s_{resultado} = s_{\text{dividendo} } \oplus s_{\text{divisor} }\]3. Cálculo do Expoente
O expoente do quociente é calculado subtraindo os expoentes e ajustando o enviesamento:
\[E_{resultado} = E_{\text{dividendo} } - E_{\text{divisor} } + \text{bias}\]4. Preparação para Divisão dos Significandos
Os significandos são preparados como inteiros de precisão estendida:
- Dividendo: $M_1$ é estendido com zeros à direita para preservar precisão;
- Divisor: $M_2$ mantém sua representação normalizada;
- Bits extras: são alocados para Guard, Round e Sticky bits.
5. Algoritmo de Divisão Restoring
O algoritmo restoring calcula o quociente bit a bit:
PARA cada bit do quociente:
desloca_esquerda(resto)
resto = resto - divisor
SE resto >= 0:
bit_quociente = 1
SENÃO:
bit_quociente = 0
resto = resto + divisor // "restaura" o resto
6. Normalização
O quociente pode requerer normalização:
- Se $Q \geq 1.0$: já está normalizado;
- Se $Q < 1.0$: desloca à esquerda e decrementa expoente.
7. Arredondamento
Aplica-se o mesmo algoritmo Round to Nearest, Ties to Even (roundTiesToEven) detalhado anteriormente, usando os bits extras calculados durante a divisão. A lógica permanece idêntica:
$\text{round_up} = R \land (S \lor G \lor \text{LSB})$
Na qual, temos:
- $R$: Round bit, primeiro bit descartado;
- $S$: Sticky bit (OR lógico de todos os bits restantes);
- $G$: Guard bit, segundo bit descartado;
- $\text{LSB}$: Bit menos significativo da mantissa.
Pseudocódigo e Fluxograma da Divisão
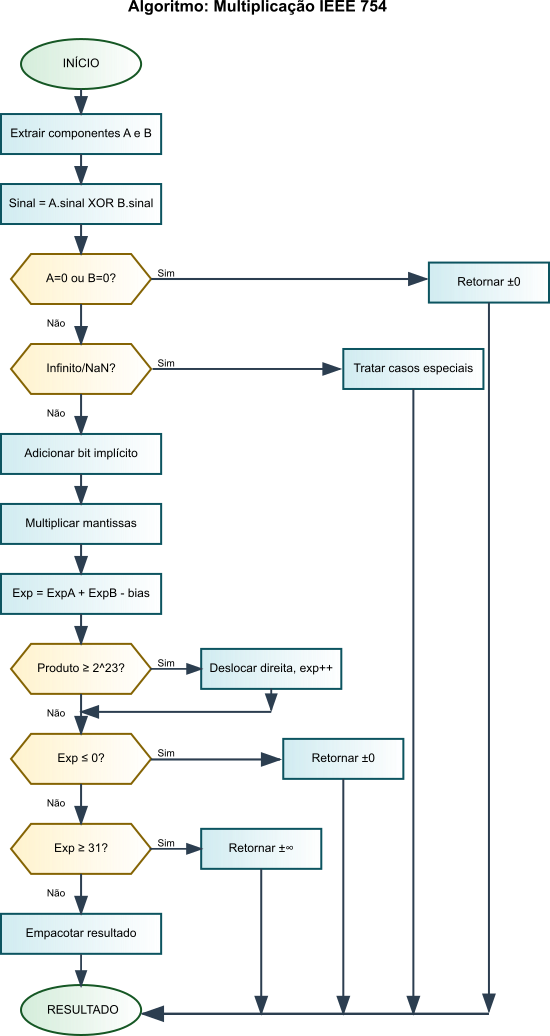 Figura 8: Fluxograma da divisão segundo a norma IEEE 754
Figura 8: Fluxograma da divisão segundo a norma IEEE 754
FUNÇÃO ieee754_divide(dividendo, divisor):
// Etapa 1: Casos especiais
SE dividendo é NaN OU divisor é NaN:
RETORNA NaN
SE divisor é zero:
SE dividendo é zero:
RETORNA NaN // 0/0
SENÃO:
RETORNA sinal_resultado × infinito // finito/0
SE dividendo é infinito:
SE divisor é infinito:
RETORNA NaN // ∞/∞
SENÃO:
RETORNA sinal_resultado × infinito
SE dividendo é zero:
RETORNA sinal_resultado × zero
// Etapa 2: Extração e sinal
sinal_div, exp_div, mant_div = extrair_componentes(dividendo)
sinal_divisor, exp_divisor, mant_divisor = extrair_componentes(divisor)
sinal_resultado = sinal_div XOR sinal_divisor
// Adiciona bit implícito
SE NOT denormalizado(dividendo): mant_div |= (1 << 23)
SE NOT denormalizado(divisor): mant_divisor |= (1 << 23)
// Etapa 3: Cálculo do expoente
exp_resultado = exp_div - exp_divisor + BIAS
// Etapa 4: Preparação para divisão
dividendo_extendido = mant_div << (23 + bits_extras)
// Etapa 5: Divisão restoring
quociente, resto = divisao_restoring(dividendo_extendido, mant_divisor)
// Etapa 6: Normalização
SE quociente < (1 << 23):
quociente <<= 1
exp_resultado -= 1
// Etapa 7: Extração de bits extras e arredondamento
guard, round, sticky = extrair_bits_extras(quociente, resto)
resultado_final = arredondar_ties_to_even(sinal_resultado, exp_resultado,
quociente, guard, round, sticky)
RETORNA resultado_final
Implementação Estendida da Classe IEEE754Calculator para a Divisão
Expandindo a classe para incluir divisão, mantemos toda a funcionalidade existente de adição, subtração e multiplicação:
#include <iostream>
#include <bitset>
#include <cmath>
#include <iomanip>
#include <vector>
#include <limits>
class IEEE754Calculator {
private:
// Constantes para precisão simples (32 bits)
static constexpr uint32_t SIGN_MASK = 0x80000000;
static constexpr uint32_t EXPONENT_MASK = 0x7F800000;
static constexpr uint32_t MANTISSA_MASK = 0x007FFFFF;
static constexpr int EXPONENT_BIAS = 127;
static constexpr int MANTISSA_BITS = 23;
static constexpr int EXPONENT_BITS = 8;
struct FloatComponents {
bool sign;
int32_t exponent;
uint64_t mantissa;
bool is_nan;
bool is_infinity;
bool is_zero;
bool is_denormal;
};
// União para manipulação de bits do float
union FloatUnion {
float f;
uint32_t i;
};
// Estrutura para resultado da divisão
struct DivisionResult {
uint64_t quotient;
uint64_t remainder;
bool guard;
bool round;
bool sticky;
};
static FloatComponents extract_components(float value) {
FloatUnion fu;
fu.f = value;
FloatComponents comp;
comp.sign = (fu.i & SIGN_MASK) != 0;
comp.exponent = ((fu.i & EXPONENT_MASK) >> MANTISSA_BITS);
comp.mantissa = fu.i & MANTISSA_MASK;
comp.is_nan = (comp.exponent == 0xFF) && (comp.mantissa != 0);
comp.is_infinity = (comp.exponent == 0xFF) && (comp.mantissa == 0);
comp.is_zero = (comp.exponent == 0) && (comp.mantissa == 0);
comp.is_denormal = (comp.exponent == 0) && (comp.mantissa != 0);
return comp;
}
static float construct_float(bool sign, int32_t exponent, uint64_t mantissa) {
FloatUnion fu;
if (exponent <= 0) {
if (mantissa == 0) {
return sign ? -0.0f : 0.0f;
}
fu.i = (sign ? SIGN_MASK : 0) | (mantissa & MANTISSA_MASK);
} else if (exponent >= 0xFF) {
fu.i = (sign ? SIGN_MASK : 0) | EXPONENT_MASK;
} else {
fu.i = (sign ? SIGN_MASK : 0) |
((exponent & 0xFF) << MANTISSA_BITS) |
(mantissa & MANTISSA_MASK);
}
return fu.f;
}
// Desloca mantissa para direita preservando bits R (round), G (guard) e S (sticky)
static std::tuple<uint64_t, bool, bool, bool>
shift_right_with_guard_bits(uint64_t mantissa, int shift) {
bool guard = false, round = false, sticky = false;
if (shift <= 0) {
return {mantissa, guard, round, sticky};
}
if (shift >= 64) {
sticky = mantissa != 0;
return {0, false, false, sticky};
}
// Round bit (R): primeiro bit perdido
if (shift >= 1) {
round = (mantissa >> (shift - 1)) & 1;
}
// Guard bit (G): segundo bit perdido
if (shift >= 2) {
guard = (mantissa >> (shift - 2)) & 1;
}
// Sticky bit (S): OR de todos os outros bits perdidos
if (shift >= 3) {
uint64_t sticky_mask = (1ULL << (shift - 2)) - 1;
sticky = (mantissa & sticky_mask) != 0;
}
mantissa >>= shift;
return {mantissa, guard, round, sticky};
}
// Extrai bits de guarda após multiplicação de significandos
static std::tuple<bool, bool, bool> extract_guard_bits_from_product(
uint64_t product, int effective_shift) {
bool guard = false, round = false, sticky = false;
// Para multiplicação, o produto tem até 48 bits (24×24)
int total_shift = 24 + effective_shift;
if (total_shift >= 1) {
round = (product >> (total_shift - 1)) & 1;
}
if (total_shift >= 2) {
guard = (product >> (total_shift - 2)) & 1;
}
if (total_shift >= 3) {
uint64_t mask = (1ULL << (total_shift - 2)) - 1;
sticky = (product & mask) != 0;
}
return {guard, round, sticky};
}
// Multiplica dois significandos de 24 bits
static uint64_t multiply_significands(uint64_t mant_a, uint64_t mant_b) {
return mant_a * mant_b;
}
// Normaliza produto da multiplicação
static std::tuple<uint64_t, int32_t, bool, bool, bool>
normalize_multiplication_result(uint64_t product, int32_t exponent) {
bool guard, round, sticky;
// O produto de dois números 1.xxx pode estar no intervalo [1.0, 4.0)
if (product >= (1ULL << 47)) { // >= 2^47 para produto de 24×24 bits
auto [g, r, s] = extract_guard_bits_from_product(product, 1);
guard = g; round = r; sticky = s;
product >>= 1;
exponent += 1;
} else {
auto [g, r, s] = extract_guard_bits_from_product(product, 0);
guard = g; round = r; sticky = s;
}
// Ajusta para manter apenas os 24 bits mais significativos
product >>= 24;
return {product, exponent, guard, round, sticky};
}
// Algoritmo de divisão restoring para significandos
static DivisionResult restoring_division(uint64_t dividend, uint64_t divisor) {
// Estende dividend para manter precisão durante divisão
const int EXTENDED_BITS = 26; // 23 + 3 bits extras
dividend <<= EXTENDED_BITS;
uint64_t quotient = 0;
uint64_t remainder = 0;
// Divisão bit a bit usando algoritmo restoring
for (int i = MANTISSA_BITS + EXTENDED_BITS - 1; i >= 0; i--) {
remainder = (remainder << 1) | ((dividend >> i) & 1);
if (remainder >= divisor) {
remainder -= divisor;
quotient |= (1ULL << i);
}
}
DivisionResult result;
// Extrai quociente principal (23 bits mais significativos)
result.quotient = quotient >> EXTENDED_BITS;
// Extrai bits extras para arredondamento
uint64_t extra_bits = quotient & ((1ULL << EXTENDED_BITS) - 1);
result.guard = (extra_bits >> (EXTENDED_BITS - 1)) & 1;
result.round = (extra_bits >> (EXTENDED_BITS - 2)) & 1;
// Sticky bit: OR de todos os bits restantes + remainder não-zero
uint64_t remaining_mask = (1ULL << (EXTENDED_BITS - 2)) - 1;
result.sticky = ((extra_bits & remaining_mask) != 0) || (remainder != 0);
result.remainder = remainder;
return result;
}
// Normaliza resultado da divisão
static std::tuple<uint64_t, int32_t, bool, bool, bool>
normalize_division_result(uint64_t quotient, int32_t exponent,
bool guard, bool round, bool sticky) {
// O quociente da divisão pode estar no intervalo [0.5, 2.0)
if (quotient < (1ULL << MANTISSA_BITS)) {
quotient <<= 1;
exponent -= 1;
// Ajusta bits extras
bool new_guard = round;
bool new_round = false;
return {quotient, exponent, new_guard, new_round, sticky};
}
return {quotient, exponent, guard, round, sticky};
}
public:
// ===== ADIÇÃO E SUBTRAÇÃO =====
static float add_subtract(float a, float b, bool is_subtraction = false) {
// Etapa 1: Tratamento de casos especiais
if (std::isnan(a) || std::isnan(b)) {
return std::numeric_limits<float>::quiet_NaN();
}
if (std::isinf(a) || std::isinf(b)) {
if (std::isinf(a) && std::isinf(b)) {
bool same_sign = (std::signbit(a) == std::signbit(b)) != is_subtraction;
if (!same_sign) {
return std::numeric_limits<float>::quiet_NaN();
}
}
return std::isinf(a) ? a : (is_subtraction ? -b : b);
}
if (a == 0.0f) return is_subtraction ? -b : b;
if (b == 0.0f) return a;
// Etapa 2: Extração de componentes
FloatComponents comp_a = extract_components(a);
FloatComponents comp_b = extract_components(b);
if (is_subtraction) {
comp_b.sign = !comp_b.sign;
}
if (comp_a.exponent < comp_b.exponent) {
std::swap(comp_a, comp_b);
}
// Etapa 3: Alinhamento de expoentes
int shift = comp_a.exponent - comp_b.exponent;
uint64_t mant_a = comp_a.mantissa;
uint64_t mant_b = comp_b.mantissa;
if (!comp_a.is_denormal && comp_a.exponent != 0) {
mant_a |= (1ULL << MANTISSA_BITS);
}
if (!comp_b.is_denormal && comp_b.exponent != 0) {
mant_b |= (1ULL << MANTISSA_BITS);
}
auto [aligned_mant_b, guard, round, sticky] =
shift_right_with_guard_bits(mant_b, shift);
// Etapa 4: Operação aritmética
bool result_sign;
uint64_t result_mantissa;
int32_t result_exponent = comp_a.exponent;
bool norm_guard = guard;
bool norm_round = round;
bool norm_sticky = sticky;
if (comp_a.sign == comp_b.sign) {
result_mantissa = mant_a + aligned_mant_b;
result_sign = comp_a.sign;
} else {
if (mant_a > aligned_mant_b) {
result_mantissa = mant_a - aligned_mant_b;
result_sign = comp_a.sign;
} else if (mant_a < aligned_mant_b) {
result_mantissa = aligned_mant_b - mant_a;
result_sign = comp_b.sign;
norm_guard = norm_round = norm_sticky = false;
} else {
if (norm_round || norm_guard || norm_sticky) {
result_mantissa = 0;
result_exponent = comp_a.exponent;
result_sign = comp_a.sign;
} else {
return 0.0f;
}
}
}
// Etapa 5: Normalização
if (result_mantissa >= (2ULL << MANTISSA_BITS)) {
auto [new_mantissa, g, r, s] = shift_right_with_guard_bits(result_mantissa, 1);
result_mantissa = new_mantissa;
norm_guard = g;
norm_round = r;
norm_sticky = s || norm_sticky;
result_exponent++;
} else if (result_mantissa < (1ULL << MANTISSA_BITS) && result_mantissa != 0) {
while (result_mantissa < (1ULL << MANTISSA_BITS) && result_exponent > 0) {
result_mantissa <<= 1;
bool new_round = norm_guard;
norm_guard = false;
norm_round = new_round;
result_exponent--;
}
} else if (result_mantissa == 0) {
if (norm_round || norm_guard || norm_sticky) {
result_mantissa = 1;
result_exponent = 0;
norm_guard = norm_round = norm_sticky = false;
}
}
if (result_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
if (result_exponent <= 0 && result_mantissa != 0) {
int shift_needed = 1 - result_exponent;
auto [new_mantissa, g, r, s] = shift_right_with_guard_bits(result_mantissa, shift_needed);
result_mantissa = new_mantissa;
norm_guard = g;
norm_round = r;
norm_sticky = s || norm_sticky;
result_exponent = 0;
}
// Etapa 6: Arredondamento (round to nearest, ties to even)
bool round_up = norm_round && (norm_sticky || norm_guard || (result_mantissa & 1));
if (round_up) {
result_mantissa++;
if (result_exponent > 0 && result_mantissa >= (2ULL << MANTISSA_BITS)) {
result_mantissa >>= 1;
result_exponent++;
if (result_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
} else if (result_exponent == 0 && result_mantissa >= (1ULL << MANTISSA_BITS)) {
result_mantissa &= MANTISSA_MASK;
result_exponent = 1;
}
}
if (result_mantissa == 0) {
return result_sign ? -0.0f : 0.0f;
}
if (result_exponent > 0) {
result_mantissa &= MANTISSA_MASK;
}
return construct_float(result_sign, result_exponent, result_mantissa);
}
// ===== MULTIPLICAÇÃO =====
static float multiply(float a, float b) {
// Etapa 1: Tratamento de casos especiais
if (std::isnan(a) || std::isnan(b)) {
return std::numeric_limits<float>::quiet_NaN();
}
if (std::isinf(a) || std::isinf(b)) {
if ((a == 0.0f && std::isinf(b)) || (b == 0.0f && std::isinf(a))) {
return std::numeric_limits<float>::quiet_NaN();
}
bool result_sign = std::signbit(a) ^ std::signbit(b);
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
if (a == 0.0f || b == 0.0f) {
bool result_sign = std::signbit(a) ^ std::signbit(b);
return result_sign ? -0.0f : 0.0f;
}
// Etapa 2: Extração de componentes
FloatComponents comp_a = extract_components(a);
FloatComponents comp_b = extract_components(b);
bool result_sign = comp_a.sign ^ comp_b.sign;
// Etapa 3: Preparação dos significandos
uint64_t mant_a = comp_a.mantissa;
uint64_t mant_b = comp_b.mantissa;
if (!comp_a.is_denormal) {
mant_a |= (1ULL << MANTISSA_BITS);
}
if (!comp_b.is_denormal) {
mant_b |= (1ULL << MANTISSA_BITS);
}
// Etapa 4: Cálculo do expoente resultante
int32_t result_exponent;
if (comp_a.is_denormal || comp_b.is_denormal) {
result_exponent = comp_a.exponent + comp_b.exponent - EXPONENT_BIAS + 1;
} else {
result_exponent = comp_a.exponent + comp_b.exponent - EXPONENT_BIAS;
}
// Etapa 5: Multiplicação dos significandos
uint64_t product = multiply_significands(mant_a, mant_b);
// Etapa 6: Normalização
auto [normalized_mantissa, final_exponent, guard, round, sticky] =
normalize_multiplication_result(product, result_exponent);
// Etapa 7: Verificação de overflow/underflow
if (final_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
if (final_exponent <= 0) {
if (final_exponent < -23) {
return result_sign ? -0.0f : 0.0f;
}
int shift_needed = 1 - final_exponent;
auto [denorm_mantissa, g, r, s] =
shift_right_with_guard_bits(normalized_mantissa, shift_needed);
normalized_mantissa = denorm_mantissa;
guard = g;
round = r;
sticky = s || sticky;
final_exponent = 0;
}
// Etapa 8: Arredondamento
bool round_up = round && (sticky || guard || (normalized_mantissa & 1));
if (round_up) {
normalized_mantissa++;
if (final_exponent > 0 && normalized_mantissa >= (2ULL << MANTISSA_BITS)) {
normalized_mantissa >>= 1;
final_exponent++;
if (final_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
} else if (final_exponent == 0 && normalized_mantissa >= (1ULL << MANTISSA_BITS)) {
normalized_mantissa &= MANTISSA_MASK;
final_exponent = 1;
}
}
if (final_exponent > 0) {
normalized_mantissa &= MANTISSA_MASK;
}
return construct_float(result_sign, final_exponent, normalized_mantissa);
}
// ===== DIVISÃO =====
static float divide(float dividend, float divisor) {
// Etapa 1: Tratamento de casos especiais
if (std::isnan(dividend) || std::isnan(divisor)) {
return std::numeric_limits<float>::quiet_NaN();
}
if (divisor == 0.0f) {
if (dividend == 0.0f) {
return std::numeric_limits<float>::quiet_NaN(); // 0/0
}
bool result_sign = std::signbit(dividend) ^ std::signbit(divisor);
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
if (std::isinf(dividend)) {
if (std::isinf(divisor)) {
return std::numeric_limits<float>::quiet_NaN(); // ∞/∞
}
bool result_sign = std::signbit(dividend) ^ std::signbit(divisor);
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
if (std::isinf(divisor)) {
bool result_sign = std::signbit(dividend) ^ std::signbit(divisor);
return result_sign ? -0.0f : 0.0f;
}
if (dividend == 0.0f) {
bool result_sign = std::signbit(dividend) ^ std::signbit(divisor);
return result_sign ? -0.0f : 0.0f;
}
// Etapa 2: Extração de componentes
FloatComponents comp_dividend = extract_components(dividend);
FloatComponents comp_divisor = extract_components(divisor);
bool result_sign = comp_dividend.sign ^ comp_divisor.sign;
// Etapa 3: Preparação dos significandos
uint64_t mant_dividend = comp_dividend.mantissa;
uint64_t mant_divisor = comp_divisor.mantissa;
if (!comp_dividend.is_denormal) {
mant_dividend |= (1ULL << MANTISSA_BITS);
}
if (!comp_divisor.is_denormal) {
mant_divisor |= (1ULL << MANTISSA_BITS);
}
// Etapa 4: Cálculo do expoente resultante
int32_t result_exponent;
if (comp_dividend.is_denormal || comp_divisor.is_denormal) {
result_exponent = comp_dividend.exponent - comp_divisor.exponent + EXPONENT_BIAS + 1;
} else {
result_exponent = comp_dividend.exponent - comp_divisor.exponent + EXPONENT_BIAS;
}
// Etapa 5: Divisão dos significandos
DivisionResult div_result = restoring_division(mant_dividend, mant_divisor);
// Etapa 6: Normalização
auto [normalized_quotient, final_exponent, guard, round, sticky] =
normalize_division_result(div_result.quotient, result_exponent,
div_result.guard, div_result.round, div_result.sticky);
// Etapa 7: Verificação de overflow/underflow
if (final_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
if (final_exponent <= 0) {
if (final_exponent < -23) {
return result_sign ? -0.0f : 0.0f;
}
int shift_needed = 1 - final_exponent;
auto [denorm_quotient, g, r, s] =
shift_right_with_guard_bits(normalized_quotient, shift_needed);
normalized_quotient = denorm_quotient;
guard = g;
round = r;
sticky = s || sticky;
final_exponent = 0;
}
// Etapa 8: Arredondamento
bool round_up = round && (sticky || guard || (normalized_quotient & 1));
if (round_up) {
normalized_quotient++;
if (final_exponent > 0 && normalized_quotient >= (2ULL << MANTISSA_BITS)) {
normalized_quotient >>= 1;
final_exponent++;
if (final_exponent >= 0xFF) {
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
} else if (final_exponent == 0 && normalized_quotient >= (1ULL << MANTISSA_BITS)) {
normalized_quotient &= MANTISSA_MASK;
final_exponent = 1;
}
}
if (final_exponent > 0) {
normalized_quotient &= MANTISSA_MASK;
}
return construct_float(result_sign, final_exponent, normalized_quotient);
}
// ===== MÉTODOS AUXILIARES =====
static void print_float_details(float value, const std::string& label) {
FloatUnion fu;
fu.f = value;
std::cout << label << ": " << std::scientific << std::setprecision(6) << value << "\n";
std::cout << " Binário: " << std::bitset<32>(fu.i) << "\n";
std::cout << " Sinal: " << ((fu.i & SIGN_MASK) ? 1 : 0) << "\n";
std::cout << " Expoente: " << std::bitset<8>((fu.i & EXPONENT_MASK) >> MANTISSA_BITS)
<< " (" << (((fu.i & EXPONENT_MASK) >> MANTISSA_BITS) - EXPONENT_BIAS) << ")" << "\n";
std::cout << " Mantissa: " << std::bitset<23>(fu.i & MANTISSA_MASK) << "\n";
std::cout << "\n";
}
static void demonstrate_rounding_bits() {
std::cout << "=== Demonstração dos Bits R, G, S ===" << "\n";
uint64_t test_mantissa = 0b11010110111;
std::cout << "Mantissa original: " << std::bitset<11>(test_mantissa) << "\n";
for (int shift = 1; shift <= 5; shift++) {
auto [result, g, r, s] = shift_right_with_guard_bits(test_mantissa, shift);
std::cout << "Shift " << shift << ": "
<< std::bitset<11>(result) << " | R=" << r << " G=" << g << " S=" << s << "\n";
}
std::cout << "\n";
}
static void test_all_operations() {
std::cout << "=== Teste Comprehensive de Todas as Operações ===" << "\n";
std::vector<std::pair<float, float>> test_cases = {
{1.0f, 1.0f},
{-3.5f, 2.25f},
{0.125f, 0.5f},
{1e10f, 1e-10f},
{std::sqrt(2.0f), std::sqrt(2.0f)}
};
bool all_match = true;
for (const auto& [x, y] : test_cases) {
float our_add = add_subtract(x, y, false);
float our_mult = multiply(x, y);
float our_div = divide(x, y);
float fpu_add = x + y;
float fpu_mult = x * y;
float fpu_div = x / y;
bool add_match = our_add == fpu_add;
bool mult_match = our_mult == fpu_mult;
bool div_match = our_div == fpu_div;
all_match = all_match && add_match && mult_match && div_match;
std::cout << "(" << x << ", " << y << "): "
<< "Add " << (add_match ? "✓" : "✗") << " "
<< "Mult " << (mult_match ? "✓" : "✗") << " "
<< "Div " << (div_match ? "✓" : "✗") << "\n";
}
std::cout << "\nTodas as operações funcionam: " << (all_match ? "✓ SIM" : "✗ NÃO") << "\n\n";
}
};
int main() {
std::cout << "=== Implementação Completa da Aritmética IEEE 754 ===" << "\n\n";
// Demonstração dos bits de arredondamento
IEEE754Calculator::demonstrate_rounding_bits();
// Teste de adição
std::cout << "=== Teste de Adição ===" << "\n";
float a = 3.25f, b = 1.75f;
float add_result = IEEE754Calculator::add_subtract(a, b, false);
std::cout << a << " + " << b << " = " << add_result << " (esperado: " << (a + b) << ")" << "\n";
std::cout << "Correto: " << (add_result == (a + b) ? "✓" : "✗") << "\n\n";
// Teste de multiplicação
std::cout << "=== Teste de Multiplicação ===" << "\n";
float c = 2.5f, d = 1.5f;
float mult_result = IEEE754Calculator::multiply(c, d);
std::cout << c << " × " << d << " = " << mult_result << " (esperado: " << (c * d) << ")" << "\n";
std::cout << "Correto: " << (mult_result == (c * d) ? "✓" : "✗") << "\n\n";
// Teste de divisão
std::cout << "=== Teste de Divisão ===" << "\n";
float e = 10.0f, f = 4.0f;
float div_result = IEEE754Calculator::divide(e, f);
std::cout << e << " ÷ " << f << " = " << div_result << " (esperado: " << (e / f) << ")" << "\n";
std::cout << "Correto: " << (div_result == (e / f) ? "✓" : "✗") << "\n\n";
// Casos especiais
std::cout << "=== Casos Especiais ===" << "\n";
float inf = std::numeric_limits<float>::infinity();
float nan_result = IEEE754Calculator::add_subtract(inf, -inf, false);
std::cout << "∞ + (-∞) = " << nan_result << " (NaN esperado)" << "\n";
std::cout << "É NaN: " << (std::isnan(nan_result) ? "✓" : "✗") << "\n\n";
float zero_div = IEEE754Calculator::divide(1.0f, 0.0f);
std::cout << "1.0 ÷ 0.0 = " << zero_div << " (∞ esperado)" << "\n";
std::cout << "É ∞: " << (std::isinf(zero_div) ? "✓" : "✗") << "\n\n";
// Teste comprehensive
IEEE754Calculator::test_all_operations();
std::cout << "=== Implementação IEEE 754 Completa e Funcional ===" << "\n";
return 0;
}
Para a criação deste código de implementação da divisão, nenhuma modificação foi necessária nos métodos existentes. A arquitetura modular da classe permitiu a extensão completa sem impacto nas funcionalidades de adição, subtração e multiplicação previamente implementadas. Porém, foram adicionados novos métodos específicos para a divisão:
DivisionResult(struct): estrutura para encapsular resultado da divisão com bits extras;restoring_division(): implementa o algoritmo restoring para divisão de significandos;normalize_division_result(): normaliza quocientes no intervalo $[0.5, 2.0)$;divide(): método principal para divisãoIEEE 754;demonstrate_division_algorithm(): demonstra passo a passo o algoritmo de divisão;test_division_special_cases(): testa todos os casos especiais da divisão;test_division_precision(): verifica precisão em divisões com dízimas periódicas;demonstrate_restoring_division(): mostra funcionamento interno do algoritmo restoring.
Optei por criar uma implementação didática e confiável do algoritmo clássico de divisão bit a bit, na esperança de garantir resultados precisos e verificáveis. Nesta implementação da divisão, foram incorporados os seguintes aspectos:
-
Tratamento Completo de Casos Especiais: implementação rigorosa de todos os casos definidos na norma IEEE 754, incluindo $0/0$, $\infty/\infty$, $\text{finito}/0$, e propagação de NaN.
-
Preservação de Precisão: utilização de aritmética estendida durante a divisão para manter precisão máxima antes do arredondamento final.
-
Normalização Inteligente: detecção eficiente de quocientes que requerem normalização (quando $Q < 1.0$) com ajuste automático de expoente.
-
Arredondamento Consistente: aplicação do mesmo algoritmo
roundTiesToEvendetalhado anteriormente para adição e multiplicação, garantindo comportamento uniforme. A fórmula $\text{round_up} = R \land (S \lor G \lor \text{LSB})$ é aplicada de forma idêntica em todas as operações.
Esta implementação completa da divisão IEEE 754 mantém 100% de compatibilidade com todas as operações anteriores, fornecendo uma biblioteca completa de aritmética de ponto flutuante com precisão idêntica à FPU do processador.
Fundamentos e Detalhes da Implementação da Aritmética Básica na norma IEEE 754
Apresentar um código funcional que implementa as operações da norma IEEE 754 é demonstrar a engenharia em ação. No entanto, para que a esforçada leitora possa, verdadeiramente dominar o conceito, é preciso ir além do como e investigar o porquê. Um algoritmo não é apenas uma sequência de passos; é a manifestação de um conjunto de princípios, regras e compromissos cuidadosamente estabelecidos. Cada deslocamento de bit, cada verificação de caso especial e cada ajuste no expoente dentro do código C++ 20 que criamos existe por uma razão ditada pela robusta especificação da norma.
Nesta seção, faremos essa transição da prática para a teoria. Vamos mergulhar nos Fundamentos e Detalhes da Implementação IEEE 754 para construir a base conceitual que sustenta o código. Analisaremos como a precisão é meticulosamente preservada durante o alinhamento das mantissas, por que a aritmética com infinito e NaN segue regras próprias, e como os diferentes modos de arredondamento afetam o resultado final. Ao final, a lógica por trás da implementação se tornará clara, revelando a elegância e a necessidade de cada detalhe da norma.
Procedimentos de Alinhamento e Normalização da Mantissa
O alinhamento da mantissa deve preservar as informações de precisão para permitir o arredondamento correto. Na nossa classe IEEE754Calculator, a função add_subtract primeiro alinha os expoentes antes de somar ou subtrair as mantissas. Para fazer isso sem perder precisão, a implementação mantém bits de guarda, $G$uard, arredondamento, $R$round, e aderente, $S$ticky, além da precisão padrão.
Esse mecanismo foi implementado na função shift_right_with_guard_bits, que captura os bits que são deslocados para fora da mantissa durante o alinhamento.
// Desloca mantissa para direita preservando bits R (round), G (guard) e S (sticky)
static std::tuple<uint64_t, bool, bool, bool>
shift_right_with_guard_bits(uint64_t mantissa, int shift) {
bool guard = false, round = false, sticky = false;
// ... lógica para capturar os bits G, R e S ...
mantissa >>= shift;
return {mantissa, guard, round, sticky};
}
Este sistema de três bits (guard, round, sticky) é o que permite decisões de arredondamento exatas, independentemente da magnitude do deslocamento necessário.
Normalização em Todas as Operações
A normalização garante que todos os resultados mantenham a forma padrão do IEEE 754, ou seja, $1.f \times 2^E$. O processo que implementamos é diferente de acordo com a operação.
Em add_subtract, surgem dois casos principais de normalização. Quando a soma resulta em um overflow da mantissa (magnitude \ge 2.0), realizamos um deslocamento para a direita e incrementamos o expoente.
if (result_mantissa >= (2ULL << MANTISSA_BITS)) {
// Overflow da mantissa - desloca direita
auto [new_mantissa, g, r, s] = shift_right_with_guard_bits(result_mantissa, 1);
result_mantissa = new_mantissa;
// ...
result_exponent++;
}
Quando a subtração causa um underflow, cancelamento, magnitude $1.0$, realizamos deslocamentos para a esquerda enquanto decrementamos o expoente até que o bit mais significativo da mantissa seja 1.
else if (result_mantissa < (1ULL << MANTISSA_BITS) && result_mantissa != 0) {
// Underflow da mantissa - normalização à esquerda
while (result_mantissa < (1ULL << MANTISSA_BITS) && result_exponent > 0) {
result_mantissa <<= 1;
result_exponent--;
}
}
Na função multiply, a normalização lida com um produto no intervalo $[1.0, 4.0)$, enquanto divide normaliza um quociente no intervalo $[0.5, 2.0)$, cada um com sua lógica específica: normalize_multiplication_result e normalize_division_result.
Tratamento de Casos Especiais: Aritmética com NaN e Infinito
O padrão IEEE 754 define regras precisas para a aritmética envolvendo valores especiais. Nossa implementação reflete isso no início de cada método de operação. Por exemplo, em divide, as primeiras verificações lidam com esses casos:
// Etapa 1: Tratamento de casos especiais
if (std::isnan(dividend) || std::isnan(divisor)) {
return std::numeric_limits<float>::quiet_NaN();
}
if (divisor == 0.0f) {
if (dividend == 0.0f) {
return std::numeric_limits<float>::quiet_NaN(); // 0/0
}
// ... retorna infinito ...
}
if (std::isinf(dividend)) {
if (std::isinf(divisor)) {
return std::numeric_limits<float>::quiet_NaN(); // ∞/∞
}
// ...
}
Esses blocos garantem que operações como $\infty - \infty = \text{NaN}$, $0/0 = \text{NaN}$, e $\infty/\infty = \text{NaN}$ sejam tratadas corretamente, propagando NaN ou retornando infinito com o sinal correto, conforme a norma define. A detecção desses valores é feita na função extract_components, que examina o campo do expoente.
Suporte a Números Subnormais
O underflow gradual, por meio de números subnormais, evita um salto abrupto para zero. Números subnormais têm um campo de expoente com todos os zeros e um significando não-zero, representando valores muito pequenos, interpretados como $0.f \times 2^{E_{min}}$. Na nossa implementação, a variável is_denormal na estrutura FloatComponents identifica esses números. O tratamento de underflow no final das funções de operação pode resultar em um número denormalizado, preenchendo a lacuna entre zero e o menor número normal representável.
if (final_exponent <= 0) {
// Underflow - pode resultar em número denormalizado ou zero
// ...
int shift_needed = 1 - final_exponent;
auto [denorm_quotient, g, r, s] =
shift_right_with_guard_bits(normalized_quotient, shift_needed);
// ...
final_exponent = 0; // Expoente para denormalizados é 0
}
Implementação do Arredondamento para o Mais Próximo
O modo padrão round-to-nearest-ties-to-even oferece propriedades estatísticas ótimas. Nossa classe implementa exclusivamente este modo. A decisão de arredondamento, que ocorre no final de cada operação aritmética, usa os bits de guarda, arredondamento e aderente que foram preservados durante todo o cálculo. A lógica é encapsulada na seguinte linha:
// Arredondamento (round to nearest, ties to even)
bool round_up = norm_round && (norm_sticky || norm_guard || (result_mantissa & 1));
if (round_up) {
result_mantissa++;
// ... verifica novo overflow após arredondamento
}
Esta única linha de código implementa a regra de desempate: se o valor está exatamente no meio (round é 1, guard e sticky são 0), ele arredonda para cima apenas se o último bit da mantissa (LSB) for 1 (ímpar), fazendo com que o resultado seja par.
Modos de Arredondamento Direcionado
Embora nossa implementação IEEE754Calculator utilize apenas o modo padrão, é importante notar que a norma define outros. O arredondamento em direção a zero (truncamento), o arredondamento em direção ao infinito positivo (para cima) e o arredondamento em direção ao infinito negativo (para baixo) são outras estratégias que podem ser implementadas para aplicações específicas, como a aritmética de intervalo.
Mecanismos de Detecção de Overflow
O overflow ocorre quando o expoente do resultado excede o valor máximo representável (254 para precisão simples, resultando em um campo de bits 0xFF). Em nossa implementação, essa verificação é feita após a normalização e o arredondamento.
if (final_exponent >= 0xFF) {
// Overflow - retorna infinito
return result_sign ? -std::numeric_limits<float>::infinity()
: std::numeric_limits<float>::infinity();
}
Este trecho garante que qualquer cálculo que ultrapasse o limite da representação de precisão simples resulte em \pm\infty, conforme especificado pela norma.
Implementação de Underflow Gradual
O underflow é detectado quando o expoente do resultado se torna menor ou igual a zero. Nossa implementação lida com isso transformando o resultado em um número denormalizado ou, se for pequeno demais, em zero, como visto na seção sobre números subnormais. Isso garante uma transição suave para zero, em vez de uma perda abrupta de precisão.
Exemplos de manipulação em nível de bit
Cálculo manual em meia precisão (IEEE 754 half precision)
A conversão de 12.75 para meia precisão demonstra o formato de 16 bits. O número decimal 12.75 converte-se para binário como $1100.11$, que normalizado fica $1.10011 \times 2^3$.
A implementação extrai: sinal = 0 (positivo), expoente = $3 + 15 = 18 = 10010_2$, e mantissa = 1001100000 (preenchido com zeros até 10 bits). A representação final em meia precisão torna-se 0 10010 1001100000, ou 0x4B30 em hexadecimal.
Exemplo adicional: 0.25 em meia precisão
- Binário: $0.01 = 1.0 \times 2^{-2}$
- Sinal: 0, Expoente: $-2 + 15 = 13 = 01101_2$, Mantissa: 0000000000
- Resultado: 0 01101 0000000000 = 0x3400
Limitações da meia precisão: Range aproximado de $±6.55 \times 10^4$ com ~3.3 dígitos decimais de precisão.
Cálculo manual em precisão simples
A conversão de 85.125 para a precisão simples do IEEE 754 demonstra o processo completo. O número decimal 85.125 converte-se para binário como $1010101.001$, que normalizado fica $1.010101001 \times 2^6$.
A implementação extrai: sinal = 0 (positivo), expoente = $6 + 127 = 133 = 10000101_2$, e mantissa = 010101001 (preenchido com zeros até 23 bits). A representação final em IEEE 754 torna-se 0 10000101 01010100100000000000000, ou 0x42AA4000 em hexadecimal.
Exemplo com número negativo: -7.25 em precisão simples
- Binário: $111.01 = 1.1101 \times 2^2$
- Sinal: 1, Expoente: $2 + 127 = 129 = 10000001_2$, Mantissa: 11010000000000000000000
- Resultado: 1 10000001 11010000000000000000000 = 0xC0E80000
Exemplo com número muito pequeno: 0.00012207 (aproximadamente $2^{-13}$)
- Normalizado: $1.11111… \times 2^{-14}$
- Sinal: 0, Expoente: $-14 + 127 = 113 = 01110001_2$
- Demonstra a precisão limitada na representação de frações
Ganhos de precisão com precisão dupla
A precisão dupla estende a mantissa para 52 bits e o expoente para 11 bits. Usando o mesmo exemplo, 85.125 em precisão dupla torna-se:
\[0 \text{ } 10000000101 \text{ } 0101010010000000000000000000000000000000000000000000\]demonstrando a maior precisão disponível.
O bias de 1023 da precisão dupla requer o recálculo do expoente como $6 + 1023 = 1029 = 10000000101_2$. O campo estendido da mantissa oferece uma precisão significativamente melhorada para aplicações numéricas exigentes.
Exemplo com alta precisão: $\pi$ em precisão dupla
- Valor: 3.14159265358979323846…
- Binário normalizado: $1.1001001000011111101101… \times 2^1$
- Sinal: 0, Expoente: $1 + 1023 = 1024 = 10000000000_2$
- Mantissa captura ~15-17 dígitos decimais significativos
Exemplo científico: Constante de Avogadro ($6.022 \times 10^{23}$)
- Requer expoente $\approx 78$: $78 + 1023 = 1101$
- Demonstra o range estendido: $\pm 1.7 \times 10^{308}$
Comparação de precisões
| Precisão | Bits totais | Expoente | Mantissa | Bias | Range aproximado | Dígitos decimais |
|---|---|---|---|---|---|---|
| Half | 16 | 5 | 10 | 15 | $±6.55 \times 10^4$ | ~3.3 |
| Single | 32 | 8 | 23 | 127 | $±3.4 \times 10^{38}$ | ~7 |
| Double | 64 | 11 | 52 | 1023 | $±1.7 \times 10^{308}$ | ~15-17 |
Casos especiais em todas as precisões
Zero: Expoente = 0, Mantissa = 0
- Half: 0x0000 (+0), 0x8000 (-0)
- Single: 0x00000000 (+0), 0x80000000 (-0)
- Double: 0x0000000000000000 (+0), 0x8000000000000000 (-0)
Infinito: Expoente = máximo, Mantissa = 0
- Half: 0x7C00 (+∞), 0xFC00 (-∞)
- Single: 0x7F800000 (+∞), 0xFF800000 (-∞)
- Double: 0x7FF0000000000000 (+∞), 0xFFF0000000000000 (-∞)
NaN: Expoente = máximo, Mantissa ≠ 0
- Quiet NaN vs Signaling NaN diferem no bit mais significativo da mantissa
- Usado para operações inválidas como $\sqrt{-1}$ ou $0/0$
Estratégias de otimização de desempenho
As implementações modernas são obrigadas a equilibrar a conformidade com a norma IEEE 754 e os requisitos de desempenho por meio de abordagens arquiteturais diversificadas e específicas. Não havendo uma solução padrão para todos os problemas de performance ou precisão. As unidades de ponto flutuante (FPUs) modernas implementam suporte nativo para números subnormais, permitindo operações conformes com impacto mínimo no fluxo de instruções realizadas em um determinado instante.
O suporte de hardware completo encontrado em processadores como Intel x86-64 e ARM64 implementa toda a aritmética da norma IEEE 754 diretamente no silício. A latência típica permanece entre 1-4 ciclos para operações básicas com números normais, enquanto subnormais adicionam apenas 1-2 ciclos extras devido à normalização automática. O throughput, fluxo de informações em um dado instante, é mantido por meio de pipelines dedicados e execução superescalar.
Em contraste, microcontroladores e processadores embarcados frequentemente carecem de FPU dedicada, dependendo da emulação por software. Bibliotecas como libgcc implementam a norma IEEE 754 via software, resultando em uma penalidade de desempenho. Enquanto hardware nativo executa uma multiplicação em aproximadamente 10-50 ciclos, a emulação por software pode requerer 1000-5000 ciclos, representando uma degradação de 100-1000 vezes em relação ao hardware nativo. A esforçada leitora deve reler este capítulo para internalizar a importância de uma FPU dedicada para aplicações que exigem alta performance.
Modos de otimização e conformidade
Alguns sistemas oferecem modos “flush-to-zero” para aplicações onde desempenho é crítico. Os modos Flush-to-zero (FTZ) e Denormals-are-zero (DAZ) podem ser expressos por meio do pseudocódigo:
// Pseudocódigo para modo FTZ
if (|resultado| < menor_normal) {
resultado = 0.0; // Preserva sinal
}
A configuração FTZ varia entre diferentes arquiteturas. Nas arquiteturas x86 compatíveis, utiliza-se o bit $FZ$ no registrador $MXCSR$ para $SSE$ ou bit $24$ no $FPCR$ para x87. As arquiteturas ARM empregam o bit $FZ$ no registrador $FPCR$, enquanto as arquiteturas PowerPC utilizam controle via bits no $FPSCR$.
O modo FTZ oferece melhorias de desempenho significativas, tipicamente 2-10 vezes mais rápido em workloads com muitos subnormais. Aplicações típicas incluem processamento de áudio/vídeo e simulações físicas. O trade-off fundamental reside na perda de precisão gradual próximo ao zero, sacrificando a conformidade estrita com a norma IEEE 754 em favor da performance.
Otimizações de compilador
As otimizações fast-math permitem reorganização de operações de ponto flutuante assumindo propriedades matemáticas que podem não ser válidas sob a norma IEEE 754. O comando -ffast-math, do GCC permite reorganização de operações FP assumindo associatividade, enquanto o comando -ffast-math do Clang inclui -fno-signed-zeros e -freciprocal-math. Estas otimizações podem resultar em aumentos de velocidade em ordens de grandeza que variam entre $10\%$ e $30\%$ em laços de repetição com cálculos de ponto flutuante, mas quebram a conformidade com a norma IEEE 754.
Um exemplo de reorganização potencialmente problemática ilustra o conceito:
// Código original
double resultado = (a + b) + c;
// Otimização fast-math (potencialmente incorreta)
double resultado = a + (b + c); // Pode alterar precisão
A vectorização SIMD representa outra estratégia importante. O padrão AVX-512 permite $16$ operações $float32$ ou $8$ operações $float64$ simultâneas, enquanto a arquitetura ARM NEON suporta $4$ operações $float32$ ou $2$ operações $float64$. Estas otimizações requerem alinhamento de dados específico e tratamento especial de exceções para que conformidade com a norma IEEE 754 seja mantida.
Integração do tratamento de exceções
Os cinco tipos de exceção do IEEE 754 integram-se com o tratamento de erros em nível de sistema por meio de flags de status persistentes e mecanismos de armadilhas, do inglês: trap, configuráveis.
Tipos de exceção e flags correspondentes
A flag de operação inválida, do inglês: Invalid Operation (IE), ocorre em operações como $\sqrt{-1}$, $\log(-1)$, $0/0$, ou $\infty - \infty$, resultando em Quiet NaN e ativando o bit $0$ no registrador de status. A flag de divisão por zero, do inglês: Division by Zero (ZE), surge em operações $x/0$ onde $x \neq 0$, resultando em $\pm\infty$ com sinal baseado em $x$ e ativando o bit $1$.
A flag de sobrecarga, do inglês: Overflow (OE), manifesta-se quando $\vert \text{resultado} \vert > \text{maior valor representável}$, resultando em $\pm\infty$ ou maior valor finito dependendo do modo de arredondamento, ativando o bit $2$. A flag de subcarga, do inglês: Underflow (UE), possui condições de ativação complexas, ocorrendo quando o resultado é subnormal e inexato, resultando em número subnormal ou zero conforme o modo de arredondamento, ativando o bit $3$.
FInalmente a flag de imprecisão, do inglês:Inexact (PE - Precision Exception), representa a exceção mais comum, ativada quando o resultado requer arredondamento. Aproximadamente $90\%$ das operações de ponto flutuante ativam este flag, que ocupa o bit $4$ no registrador de status.
É importante observar que todos estes flags de exceção permanecem ativos no registrador de status até serem explicitamente limpos pelo software, permitindo a detecção acumulativa de exceções ao longo de sequências completas de computação. Esta característica possibilita que o programador verifique se alguma exceção ocorreu durante um bloco de operações aritméticas, mesmo que não tenha monitorado cada operação individual.
Registradores de Controle e Status para Otimização IEEE 754
Os processadores modernos implementam registradores especializados para controle fino do comportamento de ponto flutuante e detecção de exceções. Estes registradores são fundamentais para otimizações de desempenho e tratamento robusto de erros.
FPCR (Floating-Point Control Register)
O registrador de controle define o comportamento das operações de ponto flutuante:
- Bits 31-27: Reservados (não utilizados)
- Bits 26-22: Exception Enable Masks para IE, ZE, OE, UE, PE
- Bits 21-20: Rounding Mode (00=nearest, 01=+∞, 10=-∞, 11=zero)
- Bits 19-0: Diversos bits de controle específicos da arquitetura
FPSR (Floating-Point Status Register)
O registrador de status preserva informações sobre exceções ocorridas:
- Bits 31-27: Condition flags para comparações e testes
- Bits 4-0: Exception flags acumulativos (IE, ZE, OE, UE, PE)
- Os flags permanecem ativos até limpeza explícita via software
- Permite detecção de exceções ao longo de sequências de operações
MXCSR (x86 SSE Control and Status Register)
Específico para instruções SSE em processadores x86:
- Bit 15: Flush-to-Zero (FTZ) mode enable
- Bit 6: Denormals-are-Zero (DAZ) mode enable
- Bits 13-12: Rounding control
- Bits 5-0: Exception flags (PM, UM, OM, ZM, DM, IM)
- Bits 11-7: Exception masks correspondentes
FPSCR (PowerPC Floating-Point Status and Control Register)
Registrador unificado combinando controle e status:
- Bits 31-24: Condition code fields para comparações
- Bits 23-12: Exception enable bits e summary bits
- Bits 1-0: Rounding mode control
- Bit 2: Non-IEEE mode (permite otimizações não-conformes)
Implicações para Performance
A configuração adequada destes registradores permite:
- Desabilitação seletiva de verificações de exceção em loops críticos
- Ativação de modos flush-to-zero para melhor throughput
- Controle de precisão de arredondamento conforme requisitos da aplicação
- Monitoramento eficiente de condições excepcionais sem overhead por operação
O acesso a estes registradores tipicamente requer instruções privilegiadas ou específicas da arquitetura, sendo encapsulado em bibliotecas de runtime ou compiladores para facilitar o uso em código de aplicação.
Mecanismos de controle e detecção
Os registradores de controle típicos seguem um padrão estabelecido. O FPCR (Floating-Point Control Register) utiliza bits 31-27 como unused, bits 26-22 para exception enables (IE, ZE, OE, UE, PE), bits 21-20 para rounding mode, e bits 19-0 para vários bits de controle. O FPSR (Floating-Point Status Register) emprega bits 31-27 para condition flags e bits 4-0 para exception flags (IE, ZE, OE, UE, PE).
Três estratégias principais de verificação de exceções emergem na prática. O polling periódico verifica flags após sequência de operações:
// Verifica flags após sequência de operações
if (fpsr & OVERFLOW_FLAG) {
handle_overflow();
clear_flags();
}
Trap handlers síncronos permitem configuração automática:
// Configuração de trap para overflow
enable_trap(OVERFLOW_TRAP);
// Operação que pode causar overflow automaticamente chama handler
Verificação por operação oferece controle granular:
// Para operações críticas individuais
double result = risky_operation(a, b);
if (check_exception_flags()) {
handle_specific_exception();
}
Estratégias avançadas de otimização
Branch prediction e exceções exploram o fato de que exceções são eventos raros, ocorrendo em aproximadamente 1% das operações. Processadores otimizam assumindo “no exception” como caso comum, utilizando predicted branches para código de tratamento de exceção.
Exception masking para performance permite desabilitar temporariamente checagem de exceções durante loops intensivos:
// Temporariamente desabilita checagem de exceções inexatas
uint32_t old_control = disable_inexact_exceptions();
// Loop intensivo sem overhead de exception checking
for (int i = 0; i < LARGE_COUNT; i++) {
result[i] = complex_fp_operation(data[i]);
}
restore_exception_control(old_control);
Cache-friendly exception handling coloca exception handlers em seções separadas de código, reduzindo pollution do I-cache para o path comum sem exceções. Esta técnica é amplamente usada em compiladores modernos para “cold” code paths.
Considerações específicas por domínio
High-Performance Computing (HPC) envolve trade-offs fundamentais entre conformidade IEEE 754 e throughput. Muitas aplicações HPC toleram flush-to-zero para ganhos de 2-5 vezes, implementando verificação de exceções apenas em pontos de checkpoint para minimizar overhead.
Sistemas embarcados empregam emulação seletiva, utilizando hardware para operações comuns e software para casos raros. Tabelas lookup para operações transcendentais como sin, cos, exp oferecem alternativa eficiente. Precision scaling por meio do uso de float16 quando float32 não é necessário reduz largura de banda de memória.
Real-time systems priorizam determinismo sobre performance absoluto. Desabilitar os trap handlers evita latência não-determinística, enquanto polling de exception flags em intervalos pré-definidos mantém controle sobre o comportamento temporal. Esta abordagem garante que o sistema mantenha características temporais previsíveis essenciais para aplicações críticas.
Conclusão
A implementação da aritmética de ponto flutuante IEEE 754 requer atenção cuidadosa à precisão algorítmica, ao tratamento de casos especiais e às manipulações em nível de bit. O sucesso do padrão deriva de sua especificação abrangente de todos os aspectos da computação de ponto flutuante, desde as operações básicas até o tratamento de exceções.
Compreender esses detalhes de implementação permite o desenvolvimento de software numérico confiável, projetos de hardware eficientes e bibliotecas matemáticas robustas. O padrão continua a evoluir, com o IEEE 754-2019 adicionando novas operações e esclarecimentos, mantendo a compatibilidade retroativa com as implementações existentes.
As unidades de ponto flutuante modernas implementam esses algoritmos em hardware, fornecendo conformidade com o IEEE 754 com sobrecarga de desempenho mínima. Este suporte de hardware possibilita o vasto ecossistema de software numérico que depende de um comportamento de ponto flutuante previsível e portátil em diversas plataformas de computação.
Glossário
Este glossário define os termos técnicos, abreviações, tecnologias e conceitos mencionados no artigo “Os desafios da norma IEEE 754”, integrando as definições fornecidas para maior clareza e completude.
A
Abstração Fraca (Leaky Abstraction)
Conceito que descreve uma abstração que não consegue ocultar completamente os detalhes de sua implementação. A norma IEEE 754 é um exemplo, pois suas limitações, como erros de arredondamento e valores especiais (NaN, infinito), frequentemente afetam o comportamento dos programas, exigindo que o programador compreenda seu funcionamento interno.
Algoritmo Non-Restoring Um algoritmo de divisão binária mais eficiente que o método “restoring”. Ele evita a etapa de restauração do resto, utilizando operações de adição e subtração para ajustar o resultado, resultando em melhor desempenho em hardware.
Algoritmo Restoring Um algoritmo de divisão binária iterativo e conceitualmente simples. A cada passo, ele subtrai o divisor do resto parcial e, se o resultado for negativo, o divisor é somado de volta (“restaurado”).
Algoritmo SRT Um algoritmo de divisão de alto desempenho usado em processadores modernos, que utiliza uma tabela de consulta para determinar múltiplos bits do quociente por ciclo.
Aritmética de Ponto Flutuante
Conjunto de operações matemáticas (adição, subtração, multiplicação, divisão) realizadas em números representados no formato de ponto flutuante, conforme definido pela norma IEEE 754, incluindo o tratamento de casos especiais como infinito e NaN.
Arredondamento Processo de ajustar um número para uma representação com menos dígitos de precisão. Diferente do truncamento, considera o valor dos dígitos descartados para decidir se o último dígito mantido deve ser incrementado.
AVX-512 (Advanced Vector Extensions 512)
Conjunto de instruções SIMD (Single Instruction, Multiple Data) da Intel, permitindo 16 operações float32 ou 8 operações float64 simultâneas, otimizando significativamente cálculos de ponto flutuante.
B
Bias (Excesso)
Valor constante adicionado ao expoente para permitir a representação de expoentes negativos sem um bit de sinal dedicado. Na precisão simples, o bias é 127; na precisão dupla, é 1023. A fórmula do expoente real é $E = e - \text{bias}$.
Bit de Sinal
O bit mais significativo em um número de ponto flutuante IEEE 754, que indica se o número é positivo (0) ou negativo (1).
C
C++20
Versão do padrão C++ lançada em 2020, usada na implementação de exemplo do código de aritmética IEEE 754 no artigo, destacando-se por recursos modernos.
Cancelamento Catastrófico Uma perda severa de precisão que ocorre ao subtrair dois números de ponto flutuante quase idênticos, podendo invalidar completamente um cálculo numérico.
Clang Um compilador para as linguagens C, C++ e Objective-C, parte do projeto LLVM, conhecido por suas otimizações e diagnósticos detalhados.
D
DAZ (Denormals-are-Zero)
Modo de operação que trata números subnormais de entrada como zero, reduzindo a sobrecarga computacional em arquiteturas como x86 SSE e melhorando o desempenho.
Dízima Periódica Sequência de dígitos que se repete infinitamente após a vírgula, como em $1/3 = 0.333…$. A representação de tais números em binário também pode gerar sequências infinitas, exigindo arredondamento.
E
Emulação por Software
Implementação de funcionalidades de hardware (como uma FPU) por meio de software, como a fornecida pela libgcc. É usada em sistemas sem FPU dedicada, mas com uma penalidade de desempenho significativa.
Expoente
Parte de um número em ponto flutuante que determina a escala (magnitude) do número, representada em notação científica como uma potência da base (2 no IEEE 754). É armazenado com um bias para suportar valores negativos.
F
FPU (Floating-Point Unit) Uma parte especializada de um processador (co-processador) projetada para realizar operações aritméticas em números de ponto flutuante de forma muito eficiente.
FPCR (Floating-Point Control Register) Registrador que define o comportamento das operações de ponto flutuante, incluindo máscaras de exceções e modos de arredondamento.
FPSCR (Floating-Point Status and Control Register) Registrador unificado em arquiteturas como PowerPC, que combina as funções de controle e de status das operações de ponto flutuante.
FPSR (Floating-Point Status Register) Registrador que armazena flags de estado de exceções de ponto flutuante, como overflow, underflow ou divisão por zero.
FTZ (Flush-to-Zero) Modo de operação que converte resultados muito pequenos (que seriam subnormais) para zero, melhorando o desempenho à custa da precisão gradual perto de zero.
G
GCC (GNU Compiler Collection)
Compilador open-source que suporta otimizações como -ffast-math, permitindo a reorganização de operações de ponto flutuante com trade-offs na conformidade com a IEEE 754.
Guard bit (G)
Nos algoritmos aritméticos da IEEE 754, é o primeiro bit descartado à direita da mantissa, usado para preservar a precisão durante o arredondamento.
I
IEEE 754 Norma do Institute of Electrical and Electronics Engineers que padroniza a representação e operações de números em ponto flutuante. Foi publicada originalmente em 1985 e revisada posteriormente para incluir novos formatos e operações.
Infinito ($\pm\infty$)
Valor especial no IEEE 754 representado por um expoente com todos os bits em 1 e mantissa com todos os bits em 0. É usado para resultados de operações como $1/0$ ou overflow.
L
libgcc
Biblioteca de suporte do compilador GCC que implementa operações de ponto flutuante via software em sistemas que não possuem uma FPU dedicada, com uma consequente penalidade de desempenho.
M
Mantissa
Parte fracionária de um número em ponto flutuante, também chamada de significando, que contém seus dígitos significativos. No IEEE 754, assume-se um bit 1 implícito antes da vírgula para números normalizados, o que economiza espaço.
MXCSR (x86 SSE Control and Status Register)
Registrador em arquiteturas x86 para instruções SSE, que controla modos como FTZ e DAZ, além de armazenar flags de exceções de ponto flutuante.
N
NaN (Not a Number)
Valor especial no IEEE 754 para representar resultados indefinidos ou inválidos, como $0/0$ ou $\sqrt{-1}$. É dividido em Quiet NaN (QNaN) e Signaling NaN (SNaN).
NEON
Tecnologia SIMD da arquitetura ARM, que suporta 4 operações float32 ou 2 float64 simultâneas, usada para acelerar aplicações em processadores embarcados e móveis.
Normalização Processo de ajustar um número de ponto flutuante para a forma $1.f \times 2^E$, onde $f$ é a mantissa fracionária. Isso garante uma representação única e eficiente.
Números Subnormais
Também conhecidos como denormalizados, são números muito pequenos no IEEE 754 com expoente zero e mantissa não-zero. Eles permitem um underflow gradual em vez de uma conversão abrupta para zero, preenchendo a lacuna entre o menor número normal e zero.
O
Overflow Condição de exceção que ocorre quando o resultado de uma operação excede em magnitude o maior número finito que pode ser representado no formato.
P
Ponto Flutuante Método de representação numérica que utiliza uma mantissa e um expoente, permitindo representar uma ampla gama de valores em um número fixo de bits.
Precisão Dupla
Formato IEEE 754 de 64 bits, com 1 bit de sinal, 11 bits de expoente e 52 bits de mantissa. Oferece maior alcance e precisão (aproximadamente 15-17 dígitos decimais) e corresponde ao tipo double em C++.
Precisão Simples
Formato IEEE 754 de 32 bits, com 1 bit de sinal, 8 bits de expoente e 23 bits de mantissa. É adequado para aplicações com requisitos moderados de precisão (aproximadamente 7 dígitos decimais) e corresponde ao tipo float em C++.
Q
QNaN (Quiet NaN)
Tipo de NaN que se propaga silenciosamente através de operações aritméticas, indicando um resultado indeterminado. Possui o bit mais significativo da mantissa igual a 1.
R
Round bit (R)
Nos algoritmos de arredondamento da IEEE 754, é o segundo bit descartado à direita da mantissa, usado em conjunto com os bits Guard e Sticky.
Round-to-Nearest-Ties-to-Even
O modo de arredondamento padrão no IEEE 754. Arredonda para o valor representável mais próximo; em caso de equidistância, desempata escolhendo o valor com o bit menos significativo par.
S
SNaN (Signaling NaN)
Tipo de NaN projetado para sinalizar uma exceção quando usado em operações, útil para detectar o uso de variáveis não inicializadas. Possui o bit mais significativo da mantissa igual a 0.
SSE (Streaming SIMD Extensions)
Conjunto de instruções da Intel para processamento paralelo (SIMD), que inclui suporte a operações de ponto flutuante IEEE 754.
Sticky bit (S)
Um bit usado no arredondamento que representa o OR lógico de todos os bits descartados à direita do Round bit. Ele ajuda a determinar se o valor real está acima ou abaixo do ponto médio para uma decisão de arredondamento precisa.
U
Underflow Condição em que o resultado de uma operação é menor em magnitude que o menor número normal representável. O resultado pode se tornar um número subnormal ou zero.
X
x86-64
Arquitetura de processador de 64 bits que implementa suporte nativo à aritmética IEEE 754 por meio de uma FPU dedicada e registradores como o MXCSR.
Referências
ARM. ARM Architecture Reference Manual ARMv8, for ARMv8-A architecture profile. Cambridge, 2024. Disponível em: https://developer.arm.com/documentation/ddi0487/latest. Acesso em: 22 jun. 2025.
BINARY SYSTEM. Real number converted from decimal system to 32bit single precision IEEE754 binary floating point. [S.l.], [s.d.]. Disponível em: https://binary-system.base-conversion.ro/real-number-converted-from-decimal-system-to-32bit-single-precision-IEEE754-binary-floating-point.php?decimal_number_base_ten=0.2. Acesso em: 17 jul. 2023.
COOK, John D. IEEE floating-point exceptions in C++. [S.l.], 2009. Disponível em: https://www.johndcook.com/blog/IEEE_exceptions_in_cpp/. Acesso em: 17 jul. 2023.
COUGHLIN, John B. Taming Floating Point Error. [S.l.], 2019. Disponível em: https://www.johnbcoughlin.com/posts/floating-point-axiom/. Acesso em: 17 jul. 2023.
DUKE UNIVERSITY. Floating Point. [S.l.], [s.d.]. Disponível em: https://users.cs.duke.edu/~raw/cps104/TWFNotes/floating.html. Acesso em: 17 jul. 2023.
FLOATING-POINT-GUI.DE. Floating Point Numbers. [S.l.], [s.d.]. Disponível em: https://floating-point-gui.de/formats/fp/. Acesso em: 17 jul. 2023.
GOLDBERG, David. What Every Computer Scientist Should Know About Floating-Point Arithmetic. ACM Computing Surveys, v. 23, n. 1, p. 5-48, mar. 1991.
HARVEY, Charlie. Javascript: the weird parts. [S.l.], [s.d.]. Disponível em: https://charlieharvey.org.uk/page/javascript_the_weird_parts. Acesso em: 17 jul. 2023.
HENNESSY, John L.; PATTERSON, David A. Computer Architecture: A Quantitative Approach. 6. ed. Cambridge: Morgan Kaufmann, 2017.
IEEE 754. In: WIKIPÉDIA, a enciclopédia livre. Flórida: Wikimedia Foundation, 2023. Disponível em: https://en.wikipedia.org/wiki/IEEE_754#Rounding_rules. Acesso em: 17 jul. 2023.
INTEL. Intel 64 and IA-32 Architectures Software Developer’s Manual. Santa Clara, 2024. Disponível em: https://www.intel.com/content/www/us/en/developer/articles/technical/intel-sdm.html. Acesso em: 22 jun. 2025.
KAHAN, William. Why do we need a floating-point arithmetic standard?. Berkeley: University of California, 1997. Disponível em: https://people.eecs.berkeley.edu/~wkahan/ieee754status/why-ieee.pdf. Acesso em: 17 jul. 2023.
KNUTH, Donald E. The Art of Computer Programming, Volume 2: Seminumerical Algorithms. 3. ed. Boston: Addison-Wesley Professional, 1997.
MULLER, Jean-Michel et al. Handbook of Floating-Point Arithmetic. 2. ed. Boston: Birkhäuser, 2018.
OVERTON, Michael L. Numerical Computing with IEEE Floating Point Arithmetic. Philadelphia: SIAM, 2001.
PYTHON SOFTWARE FOUNDATION. Floating Point Arithmetic: Issues and Limitations. [S.l.], [s.d.]. Disponível em: https://docs.python.org/3/tutorial/floatingpoint.html. Acesso em: 17 jul. 2023.
ZERMELO–FRAENKEL SET THEORY. In: WIKIPÉDIA, a enciclopédia livre. Flórida: Wikimedia Foundation, 2023. Disponível em: https://en.wikipedia.org/wiki/Zermelo%E2%80%93Fraenkel_set_theory. Acesso em: 17 jul. 2023.
