Transformers - embeddings Distribuídos

Superando Limitações: A Necessidade de Representações Distribuídas
“you shall know a word by the company it keeps” — J.R. Firth
Nos artigos anteriores, exploramos técnicas de vetorização como Bag-of-Words (BoW) e TF-IDF, bem como modelos probabilísticos N-gram. Apesar da utilidade dessas abordagens, a atenta leitora devem lembrar que elas apresentam limitações significativas:
-
Alta dimensionalidade e esparsidade: as representações baseadas em BoW e TF-IDF geram vetores extremamente esparsos em espaços de alta dimensão, cardinalidade do vocabulário, resultando em matrizes enormes majoritariamente preenchidas com zeros.
-
Ausência de semântica: não capturam relações de similaridade ou analogia entre palavras. Por exemplo,
reierainhapodem ser tão diferentes quantoreiemaçã. -
Sem generalização: o modelo não consegue inferir nada sobre palavras que não aparecem no corpus de treinamento ou que aparecem raramente.
-
Contexto limitado: mesmo os modelos N-gram capturam apenas dependências locais em janelas pequenas, ignorando relações de longo alcance.
Para superar essas limitações, precisamos de representações mais densas e de menor dimensionalidade que capturem relações semânticas entre palavras, permitam generalização para palavras raras ou novas e que tenham capacidade de modelar informações contextuais. Sim! A amável leitora teve a impressão correta: eu quero a perfeição, ou chegar o mais perto possível.
O avanço fundamental nessa direção foi introduzido por Tomas Mikolov e seus colegas no Google em 2013 com o Word2Vec, que propôs duas arquiteturas inovadoras para gerar **embeddings distribuídos de palavras: o **Continuous Bag-of-Words (CBoW) e o **SkipGram**. Que são os algoritmos que discutiremos nesta seção.
embeddings Distribuídos: Nova Perspectiva para Representação de Palavras
Antes que a afeita leitora mergulhe nos mares dos algoritmos específicos dos embeddings distribuídos, precisamos tentar entender o conceito fundamental da representações distribuídas.
Em abordagens tradicionais como Bag-of-Words, frequentemente utilizamos, implícita ou explicitamente, vetores One-Hot para representar palavras. Nesta representação, cada palavra corresponde a um vetor de tamanho igual ao vocabulário ($\vert V \vert $), contendo $1$ na posição única associada àquela palavra e $0$ em todas as outras. Só para lembrar, nós vimos estas representações inocentes em detalhes no artigo.
Considerando o One-Hot poderíamos definir um vocabulário hipotético de $5$ palavras por:
\[V = \{\text{gato}, \text{cachorro}, \text{pássaro}, \text{corre}, \text{dorme}\}\]a representação One-Hot de cada palavra será dada por:
gato= $[1, 0, 0, 0, 0]$;cachorro= $[0, 1, 0, 0, 0]$;pássaro= $[0, 0, 1, 0, 0]$;corre= $[0, 0, 0, 1, 0]$;dorme= $[0, 0, 0, 0, 1]$.
Vamos rever rapidamente as limitações dessa abordagem:
-
Ortogonalidade e Ausência de Semântica: o produto escalar entre quaisquer dois vetores One-Hot distintos é zero ($v_{palavra1} \cdot v_{palavra2} = 0\;$). Isso implica que todas as palavras são igualmente diferentes umas das outras em um dado espaço vetorial. Ou seja, no espaço vetorial formado pelos vetores que representam as palavras não há noção de similaridade. A palavra
gatoestá tão distante decachorroquanto decorre. -
Alta Dimensionalidade e Esparsidade: a dimensão do vetor cresce linearmente com o tamanho do vocabulário, que, em casos reais, pode facilmente chegar a milhões. Isso resulta em vetores extremamente longos e esparsos, quase inteiramente preenchidos por zeros. Cada vetor tem apenas um $1$.
-
Ineficiência Computacional e de Memória: armazenar e processar esses vetores gigantes e esparsos é computacionalmente caro e ineficiente.
Para superar essas limitações, buscamos representações mais ricas e eficientes. Entram em cena as representações distribuídas, também conhecidas como word **embeddings**.
A ideia central por trás dessas representações está alinhada com a hipótese distribucional: o significado de uma palavra pode ser inferido a partir dos contextos em que ela costuma aparecer. Um conceito que tem origem no trabalho de J.R. Firth A Synopsis of Linguistic Theory” publicada em 1957, que foi amplamente discutido por Zellig Harris na década de 1950 e 1960. Segundo Firth, o significado de uma palavra é determinado por seu uso em contextos específicos, e não por definições fixas. Ou seja, para ele, o significado de uma palavra está relacionado à sua tendência de colocação com outras palavras.
Para encontrar esta relação entre as palavras, em vez de um único indicador, usamos vetores densos e de dimensão muito menor, tipicamente 50 a 300 dimensões, para codificar as palavras.
A criativa leitora pode fazer uma analogia: pense na representação One-Hot como um painel com um interruptor dedicado para cada palavra. Apenas um pode estar ligado por vez. Já a representação distribuída seria como um painel de mixagem de áudio com vários controles deslizantes. A identidade de uma palavra será definida pela combinação única das posições de todos esses controles. Todos os controles tem um papel na definição do som, ou significado, da palavra, mesmo que alguns possam ter um impacto maior do que outros.
Chamamos esta representação de distribuída porque o significado, ou melhor as características, em inglês features, de uma palavra não estão localizados em uma única dimensão, mas sim distribuídos por todas as dimensões do vetor. Cada elemento do vetor contribui um pouco para a representação geral, capturando nuances semânticas e sintáticas.
Voltando ao nosso vocabulário, uma representação distribuída hipotética poderia ser dada por:
gato= $[0.2, -0.4, 0.7, -0.2, 0.1, \cdots]$;cachorro= $[0.1, -0.3, 0.8, -0.1, 0.2, \cdots]$;pássaro= $[-0.1, -0.5, 0.3, 0.1, 0.4, \cdots]$;corre= $[0.0, 0.6, -0.1, 0.8, -0.3, \cdots]$;dorme= $[-0.3, 0.2, -0.5, -0.5, 0.6, \cdots]$.
Observe como gato e cachorro, semanticamente próximos mesmo nos nossos vetores hipotéticos, compartilham alguns padrões. Valores relativamente altos na 3ª dimensão, baixos na 2ª. Já os vetores de corre e dorme, verbos, possuem padrões distintos dos vetores dos animais. Nesta representação os valores exatos não importam tanto quanto as relações que podem existir entre os vetores. Nestas relações está a mágica dos **embeddings distribuídos**.
A esforçada leitora deve entender que essas dimensões, os elementos do vetor, não recebem rótulos pré-definidos como ser animal ou ação. Pelo contrário, o modelo de treinamento, como o Word2Vec que veremos a seguir, aprende essas representações ao analisar vastas quantidades de texto.
As dimensões dos vetores acabam capturando características latentes, ocultas, e relações complexas entre palavras, simplesmente tentando prever palavras em seus contextos. Contudo, nada impede que nós, a posteriori tentemos interpretar o que algumas dimensões, ou suas combinações, podem significar. Sem esquecer, jamais, que estes significados emergem natural e independentemente durante o processo de aprendizado.
Essa capacidade de aprender representações significativas a partir do contexto resulta em vetores com propriedades notáveis, ausentes na representação One-Hot e em outras abordagens tradicionais. Tais como:
-
Similaridade semântica: palavras semanticamente similares terão representações vetoriais próximas no espaço vetorial. Quando usamos métricas como similaridade de cosseno para medir essa similaridade. Por exemplo, em um treinamento real os vetores para
gatoecachorroestarão mais próximos entre si do que do vetor paratelefone. -
Relações analógicas: as representações distribuídas capturam relações que podem ser expressas por operações vetoriais simples. O exemplo clássico é:
\[\text{vec}(\text{"rei"}) - \text{vec}(\text{"homem"}) + \text{vec}(\text{"mulher"}) \approx \text{vec}(\text{"rainha"})\]Ou ainda, para capitais e países:
\[\text{vec}(\text{"Paris"}) - \text{vec}(\text{"França"}) + \text{vec}(\text{"Itália"}) \approx \text{vec}(\text{"Roma"})\] -
Generalização: palavras raras, ou mesmo fora do vocabulário de treinamento, podem ter embeddings estimados de qualidade razoável se ocorrerem em contextos similares a palavras mais comuns. técnicas como FastText lidam bem com isso.
FastText é uma técnica avançada de word embedding desenvolvida pelo Facebook AI Research (FAIR) que resolve o problema de palavras raras ou desconhecidas representando cada palavra como um conjunto de n-gramas de caracteres.
Enquanto modelos como Word2Vec atribuem um vetor único para cada palavra do vocabulário, o FastText quebra as palavras em componentes menores, subpalavras, capturando assim a estrutura morfológica interna das palavras. Este método aprende representações de N-grams de caracteres e representa palavras como a soma desses vetores de N-grams.
Para palavras não encontradas no treinamento, o FastText pode produzir embeddings de boa qualidade ao combinar os vetores de seus N-grams, gerando representações significativas mesmo para palavras completamente novas. Permitindo a generalização do modelo para vocabulários desconhecidos baseada na similaridade estrutural com palavras conhecidas.
\[\mathbf{v}_w = \sum_{g\in\mathcal{G}_w} \mathbf{z}_g\]Neste caso, $\mathbf{v}_w$ é o vetor final da palavra, $\mathcal{G}_w$ são todos os N-grams da palavra, e $\mathbf{z}_g$ é o vetor de cada N-grams.
-
Transferência de aprendizado: embeddings pré-treinados em grandes volumes de texto, como bancos de notícias, livros ou a Wikipédia, podem ser carregados e reutilizados como ponto de partida em tarefas de processamento de linguagem natural, mesmo com conjuntos de dados menores para a tarefa específica.
Estas quatro propriedades tornam as representações distribuídas uma ferramenta robusta, servindo de base para modelos mais complexos como LSTMs e Transformers.
LSTM (Long Short-Term Memory) é um tipo especializado de rede neural recorrente (RNN) projetada para superar o problema de desvanecimento de gradiente em RNNs tradicionais, permitindo que a rede aprenda dependências de longo prazo em dados sequenciais.
As LSTMs possuem uma arquitetura única com três “portas” (gates) que controlam o fluxo de informação:
- Porta de esquecimento (forget gate): Decide qual informação da célula de memória deve ser descartada
- Porta de entrada (input gate): Controla quais novos valores serão armazenados na célula de memória
- Porta de saída (output gate): Determina quais informações da célula serão emitidas como saída
O componente central é a célula de memória (cell state), que atua como uma esteira transportadora de informações, permitindo que informações relevantes fluam ao longo da sequência com poucas modificações, enquanto outras informações são filtradas pelas portas.
Esta estrutura permite que as LSTMs mantenham informações por períodos mais longos, tornando-as particularmente eficazes para aplicações como: processamento de linguagem natural; reconhecimento de fala; tradução automática; geração de texto; análise de séries temporais e classificação de sequências. Matematicamente, as operações de uma LSTM podem ser descritas por:
\[f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)\] \[i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)\] \[\tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)\] \[C_t = f_t * C_{t-1} + i_t * \tilde{C}_t\] \[o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)\] \[h_t = o_t * \tanh(C_t)\]Na qual, $f_t$, $i_t$, e $o_t$ representam as ativações das portas de esquecimento, entrada e saída, respectivamente.
A Figura 1 ilustra a diferença entre as representações One-Hot e distribuídas. A representação One-Hot é esparsa e de alta dimensão, enquanto a representação distribuída é densa e de baixa dimensão, capturando relações semânticas entre palavras.
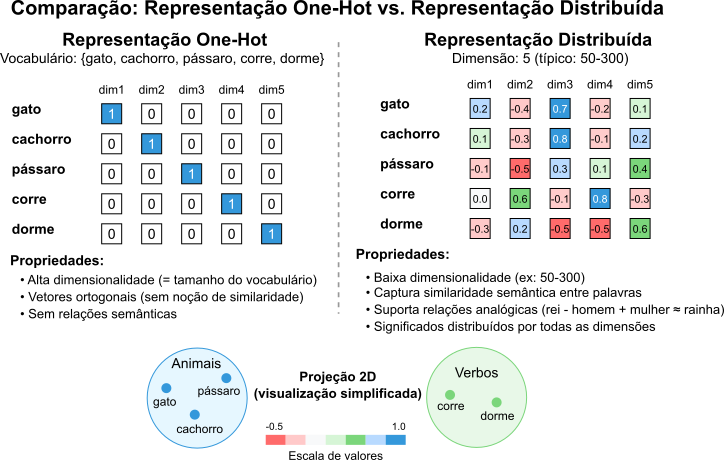
Figura 1: Comparação entre Representação One-Hot e Distribuída de Palavras
A seguir, exploraremos como o Word2Vec consegue aprender esses vetores densos e significativos.
Word2Vec: Aprendendo Representações a partir do Contexto
A primeira coisa que deve chamar a atenção da esforçada leitora é que o Word2Vec não é um único algoritmo, mas uma família de modelos com duas variantes principais: Continuous Bag-of-Words (CBoW) e **SkipGram**. Ambos compartilham a mesma ideia fundamental: aprender representações vetoriais de palavras ao prever palavras dentro de uma janela de contexto.
A ideia central de suporte do Word2Vec é aproveitar a hipótese distribucional: palavras que aparecem em contextos similares tendem a ter significados similares. Assim, o modelo aprende representações vetoriais treinando uma rede neural rasa para uma tarefa de predição.
Uma rede neural rasa (shallow neural network) é uma rede neural artificial com poucas camadas entre a entrada e a saída. Tipicamente apenas uma camada oculta, diferente das redes neurais profundas que podem ter dezenas ou centenas de camadas.
O processo geral do Word2Vec pode ser sintetizado em três passos:
- Cada palavra no vocabulário recebe inicialmente um vetor aleatório;
- Uma rede neural simples, com apenas uma camada oculta, é treinada para uma tarefa de predição;
- Após o treinamento, os vetores de palavras na camada de entrada ou, em algumas implementações, na camada oculta, são usados como os embeddings finais.
A genialidade está na simplicidade: não estamos realmente interessados na tarefa de predição em si, mas nos vetores que a rede aprende durante o processo. Mesmo a simplicidade precisa ser estudada.
Conceitos Básicos
Antes que a afoita leitora mergulhe nos algoritmos, vamos ver alguns conceitos básicos qeu servirão para fundamentar o entendimento do Word2Vec. Três conceitos são indispensáveis:
-
Janela de Contexto: ambos CBoW e SkipGram operam em janelas de contexto. Uma janela deslizante que passa pelo texto, definindo para cada posição uma palavra-alvo e seu contexto. No documento
O gato preto corre pelo jardimse tivermos uma janela de tamanho $2$, para a palavra-alvopreto, o contexto desta palavra seria dado por $[\text{gato}, \text{corre}]$. A Figura 2 permite que a atenta leitora visualize o conceito de janela de contexto.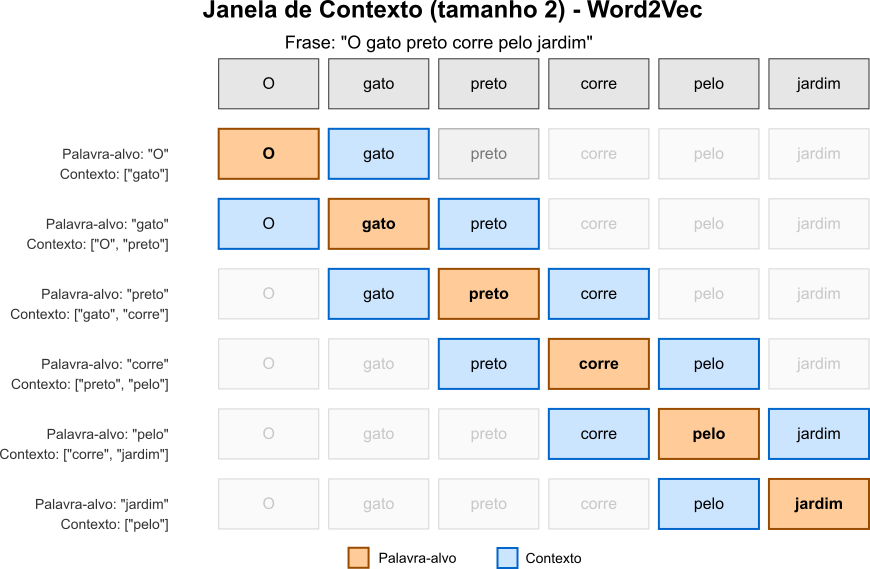
Figura 2: Visualização da janela de contexto deslizante no Word2Vec com tamanho $c=2$. Cada linha representa uma etapa do algoritmo, onde a palavra em destaque (laranja) é a palavra-alvo $w_t$, e as palavras em azul compõem o contexto $Context(w_t)$ dentro da janela de tamanho $2c$. No modelo SkipGram, o algoritmo tenta prever as palavras do contexto a partir da palavra-alvo, gerando pares de treinamento, enquanto no modelo CBoW, o algoritmo tenta prever a palavra-alvo a partir da média dos vetores das palavras do contexto.
-
Arquitetura da Rede Neural: em sua forma mais básica, a rede neural do Word2Vec tem a seguinte estrutura:
- Camada de entrada: representa a(s) palavra(s) de contexto ou a palavra-alvo;
- Camada oculta: uma camada linear (sem função de ativação);
- Camada de saída: uma camada softmax que produz probabilidades sobre o vocabulário.
As matrizes de pesos entre as camadas são o que realmente nos interessa:
- $W_{entrada}$: Matriz de dimensão $\vert V \vert \times d$, onde $\vert V \vert$ é o tamanho do vocabulário e $d$ é a dimensão dos embeddings;
- $W_{saída}$: Matriz de dimensão $d \times \vert V \vert$.
A Figura 3 sintetiza a arquitetura da rede neural do Word2Vec.
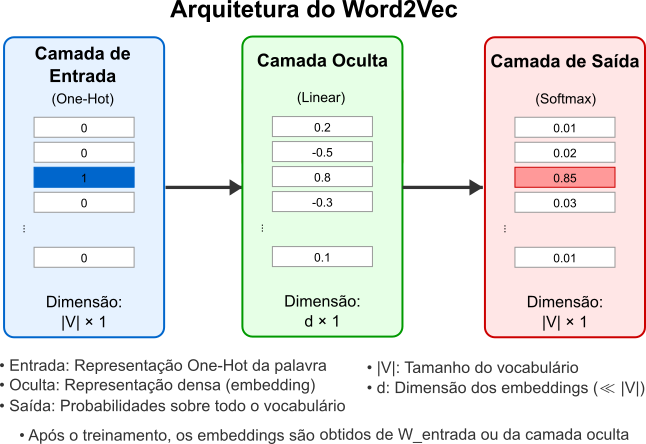
Figura 3: Arquitetura básica da rede neural do Word2Vec.
A rede consiste em três camadas: a camada de entrada que recebe um vetor One-Hot de dimensão $ \vert V \vert $ (onde $ \vert V \vert $ é o tamanho do vocabulário), uma camada oculta linear de dimensão $d$ que representa o embedding da palavra, e uma camada de saída com função softmax que produz probabilidades para cada palavra do vocabulário. As matrizes de pesos $W_{entrada}$ (dimensão $ \vert V \vert \times d$) e $W_{saída}$ (dimensão $d \times \vert V \vert $) conectam estas camadas. Após o treinamento, os vetores de palavras podem ser extraídos da matriz $W_{entrada}$ ou da camada oculta.
-
O Problema da Suavização com Softmax: a função softmax na camada de saída é definida por:
Nesta equação temos:
- $w_O$ é a palavra de saída (a prever);
- $w_I$ é a palavra de entrada;
- $v_{w}$ é o vetor de entrada para a palavra $w$;
- $v’_{w}$ é o vetor de saída para a palavra $w$.
Esta formulação apresenta um desafio computacional significativo. O denominador exige o cálculo de $\exp(v’{w} \cdot v{w_I})$ para cada palavra $w$ no vocabulário $V$. Com vocabulários que facilmente ultrapassam 100.000 palavras em aplicações reais, cada atualização de gradiente se torna extremamente custosa. Além disso, durante o treinamento, para cada exemplo, precisamos calcular os gradientes para todos os parâmetros dos vetores de todas as palavras no denominador, mesmo que a maioria tenha contribuição negligenciável para o resultado final. Finalmente, manter em memória os vetores para todas as palavras do vocabulário durante o cálculo da função softmax e seus gradientes pode exceder os recursos disponíveis para treinamento.
Estes problemas criam um gargalo computacional que motivou o desenvolvimento de aproximações mais eficientes como Negative Sampling e Hierarchical Softmax, que reduzem drasticamente a complexidade do treinamento de $O(\vert V \vert )$ para $O(k)$ ou $O(\log \vert V \vert )$, respectivamente, onde $k \ll \vert V \vert $ é o número de amostras negativas.
O Negative Sampling transforma o problema de predição multiclasse, prever uma palavra entre milhares ou milhões, em múltiplos problemas de classificação binária, reduzindo drasticamente a complexidade computacional de $O(\vert V \vert)$ para $O(k)$, onde $k$ é tipicamente um número pequeno ($5$-$20$).
O Hierarchical Softmax usa uma estrutura de árvore binária de Huffman para representar o vocabulário, permitindo calcular a probabilidade de uma palavra com complexidade $O(\log \vert V \vert)$ ao invés de $O( \vert V \vert)$.
Continuous Bag-of-Words (CBoW)
No CBoW, o modelo usa o contexto, palavras circundantes, para prever a palavra-alvo central. A palavra Continuous se refere à natureza densa e contínua dos vetores de embeddings, diferentemente do Bag-of-Words tradicional que usa vetores esparsos. Como vimos anteriormente, o CBoW tenta prever a palavra-alvo a partir de um conjunto de palavras de contexto. A ideia é que, ao usar várias palavras de contexto, o modelo pode capturar melhor o significado da palavra-alvo. Para tanto, o CBoW usa uma janela de contexto que abrange palavras antes e depois da palavra-alvo da seguinte forma:
Dada uma sequência de palavras de treinamento $w_1, w_2, …, w_T$, o objetivo é maximizar a log-probabilidade:
\[\frac{1}{T} \sum_{t=1}^{T} \log p(w_t \vert w_{t-c}, ..., w_{t-1}, w_{t+1}, ..., w_{t+c})\]Neste caso, a expressão log-probabilidade refere-se ao logaritmo natural da probabilidade, que será utilizado no lugar da probabilidade direta. As probabilidades referentes a uma determinada palavra podem ser extremamente pequenas, especialmente em vocabulários grandes, o que pode causar problemas de underflow em computadores. Como o logaritmo converte produtos em somas, simplifica as operações matemáticas, já que $\log(a \times b) = \log(a) + \log(b)$. O que reduz o custo computacional porque o modelo precisa multiplicar probabilidades condicionais com frequência. Além disso, como a função logarítmica é monotonicamente crescente, maximizar o logaritmo da probabilidade é equivalente a maximizar a probabilidade original, porém com benefícios computacionais. Por fim, as derivadas da log-probabilidade em relação aos parâmetros do modelo geralmente resultam em expressões mais simples, facilitando a implementação do algoritmo de gradiente descendente. A persistente leitora não pode esquecer que o gradiente é a direção de maior crescimento da função, e o logaritmo preserva essa propriedade. Assim, o gradiente da log-probabilidade em relação aos parâmetros do modelo é proporcional ao gradiente da probabilidade original.
A arquitetura específica do CBoW é:
- Entradas: Vetores One-Hot para cada palavra de contexto;
- Projeção: Os vetores das palavras de contexto são projetados para a camada oculta e somados (ou tirada a média);
- Saída: Predição da palavra central via softmax.
Em termos matemáticos, dado um contexto $Context(w_t)$ para uma palavra-alvo $w_t$, queremos maximizar:
\[p(w_t \vert Context(w_t)) = \frac{\exp(v'_{w_t}h)}{\sum_{w \in V} \exp(v'_{w}h)}\]Messe caso, $h = \frac{1}{2c} \sum_{-c \leq j \leq c, j \neq 0} v_{w_{t+j}}$ é a representação do contexto (média dos vetores de contexto). A Figura 4 ilustra a arquitetura do CBoW.
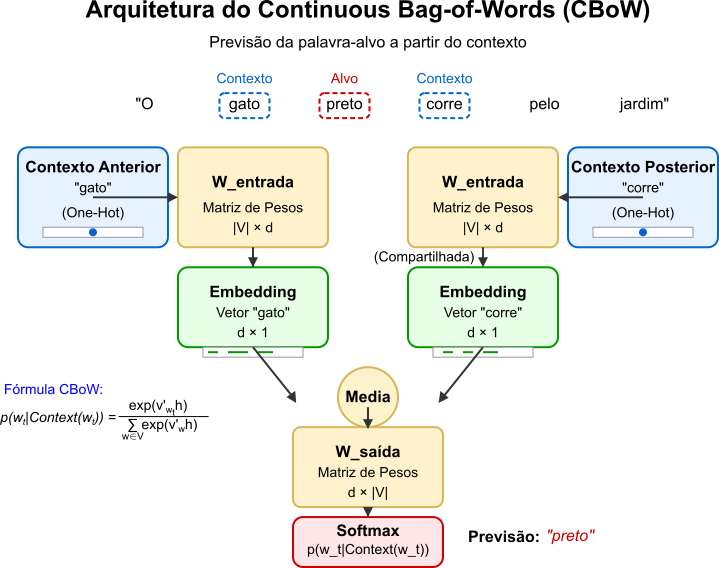
Figura 4: Arquitetura do modelo Continuous Bag-of-Words (CBoW) que implementa o princípio “você conhecerá uma palavra pela companhia que ela mantém”. O diagrama ilustra como os vetores One-Hot das palavras de contexto são transformados em embeddings densos através de uma matriz de pesos compartilhada, combinados pela operação de média para formar uma representação única do contexto, e finalmente utilizados para prever a palavra-alvo através de uma função softmax.
Exemplo de Treinamento com CBoW
Vamos ilustrar o processo com um exemplo simples. Considere a frase:
$D_1$ = O gato preto corre pelo jardim
Considerando uma janela de tamanho $1$, obteríamos os seguintes pares contexto-alvo:
- [
gato] →O; - [
O,preto] →gato; - [
gato,corre] →preto; - [
preto,pelo] →corre; - [
corre,jardim] →pelo; - [
pelo] →jardim.
Com uma janela de contexto de tamanho $1$, o algoritmo CBoW considera uma palavra à esquerda e uma palavra à direita da palavra-alvo (quando disponíveis). Os pares listados em $1, 2, 3, 4, 5, 6$ resultam da aplicação sistemática desta janela deslizante. Cada palavra na frase se torna a palavra-alvo uma vez, com seu contexto formado pelas palavras adjacentes. Nas extremidades da frase (pares $1$ e $6$), o contexto contém apenas uma palavra, pois não há palavras disponíveis de um dos lados. Observe que no exemplo $2$, a palavra-alvo gato tem como contexto O e preto porque o algoritmo define uma janela que abrange uma palavra antes e uma palavra depois da palavra-alvo gato, portanto O e preto são as palavras que aparecem nessa janela.
A aplicação do Continuous Bag-of-Words (CBoW) ao item $3$ do exemplo pode ser realizada da seguinte forma:
-
Converter as palavras de contexto em vetores One-Hot: considerando o vocabulário limitado do nosso exemplo teríamos:
\[V = \{\text{o}, \text{gato}, \text{preto}, \text{corre}, \text{pelo}, \text{jardim}, \text{cachorro}\}\]com $\vert V \vert = 7$. Neste caso, os vetores One-Hot serão:
\[\text{gato} = [0, 1, 0, 0, 0, 0, 0]\]e
\[\text{corre} = [0, 0, 0, 1, 0, 0, 0]\] -
Projetar para obter os vetores de embedding: com dimensão de embedding $d = 4$ e a matriz $W_{\text{entrada}}$.
Para este exemplo, a matriz $W_{\text{entrada}}$, de dimensão $ \vert V \vert \times d = 7 \times 4$, é inicializada com valores fictícios que simulam uma inicialização aleatória, como é comum em implementações reais do Word2Vec. Em um treinamento real, os elementos desta matriz seriam inicializados com pequenos valores aleatórios, geralmente extraídos de uma distribuição uniforme ou normal, e ajustados durante o treinamento via gradiente descendente. Os valores apresentados aqui são escolhidos para simplificar os cálculos e ilustrar o processo.
A dimensão do embedding ($d = 4$) no contexto do modelo Word2Vec refere-se ao tamanho do vetor que representa cada palavra no espaço vetorial.
A escolha de $d = 4$ foi realizada para fins didáticos, tornando os cálculos mais simples e fáceis de acompanhar manualmente. Em aplicações reais, as dimensões típicas de embeddings variam entre $50$ e $300$. A escolha da dimensionalidade do embedding envolve o estudo e a determinação de um ponto de equilíbrio entre complexidade computacional e expressividade do modelo. Considere:
- Dimensões menores (como $d = 4$ no exemplo):
- computacionalmente mais eficientes;
- requerem menos memória;
- mais fáceis de visualizar e entender;
- porém limitados na capacidade de capturar relações semânticas complexas.
- Dimensões maiores (como $d = 100$ ou $d = 300$ em aplicações reais):
- capturam relações semânticas mais ricas;
- melhor capacidade de generalização;
- maior expressividade para representar nuances linguísticas;
- porém, computacionalmente mais caros.
A matriz $W_{\text{entrada}}$ contém os vetores de embedding inicializados aleatoriamente para cada palavra no vocabulário. Para nosso exemplo, assumimos:
\[W_{\text{entrada}} = \begin{bmatrix} 0.1 & 0.2 & -0.1 & 0.3 \\ 0.2 & -0.4 & 0.7 & -0.2 \\ 0.4 & -0.3 & 0.1 & 0.5 \\ 0.0 & 0.6 & -0.1 & 0.8 \\ -0.3 & 0.2 & -0.5 & -0.5 \\ 0.5 & 0.1 & 0.3 & -0.2 \\ 0.1 & -0.3 & 0.8 & -0.1 \end{bmatrix}\]Os vetores de embedding são obtidos multiplicando os vetores One-Hot pela matriz $W_{\text{entrada}}$:
\[v_{\text{gato}} = [0, 1, 0, 0, 0, 0, 0] \times W_{\text{entrada}} = [0.2, -0.4, 0.7, -0.2]\]e
\[v_{\text{corre}} = [0, 0, 0, 1, 0, 0, 0] \times W_{\text{entrada}} = [0.0, 0.6, -0.1, 0.8]\] - Dimensões menores (como $d = 4$ no exemplo):
-
Calcular a média dos vetores de contexto: neste caso, temos os vetores de contexto
\[h = \frac{v_{\text{gato}} + v_{\text{corre}}}{2} = \frac{[0.2, -0.4, 0.7, -0.2] + [0.0, 0.6, -0.1, 0.8]}{2}\] \[h = \frac{[0.2, 0.2, 0.6, 0.6]}{2}\] \[h = [0.1, 0.1, 0.3, 0.3]\]gatoecorre. Portanto, a média dos vetores de contexto será: -
Multiplicar pela matriz de saída para obter scores: A matriz $W_{\text{saída}}$ também é inicializada aleatoriamente e mapeia da dimensão do embedding ($d=4$) para o tamanho do vocabulário ($ \vert V \vert = 7$):
Assim como $W_{\text{entrada}}$, a matriz $W_{\text{saída}}$, de dimensão $d \times \vert V \vert = 4 \times 7$, é inicializada com valores fictícios para este exemplo, representando uma inicialização aleatória típica. Em um cenário real, seus elementos seriam inicializados aleatoriamente e otimizados durante o treinamento para mapear os vetores de embedding para probabilidades sobre o vocabulário.
\[W_{\text{saída}} = \begin{bmatrix} 0.2 & 0.1 & 0.5 & -0.3 & 0.3 & -0.2 & 0.4 \\ 0.1 & 0.2 & -0.2 & 0.4 & 0.3 & 0.1 & -0.3 \\ 0.3 & -0.2 & 0.4 & 0.1 & -0.1 & 0.5 & 0.2 \\ -0.1 & 0.4 & 0.3 & 0.2 & 0.5 & 0.1 & 0.1 \end{bmatrix}\]Calculamos os scores $z = h \times W_{\text{saída}}$: $z = [0.1, 0.1, 0.3, 0.3] \times W_{\text{saída}}$
\[\begin{align*} z_0 &= (0.1)(0.2) + (0.1)(0.1) + (0.3)(0.3) + (0.3)(-0.1) \\ &= 0.02 + 0.01 + 0.09 - 0.03 = 0.09 \\ z_1 &= (0.1)(0.1) + (0.1)(0.2) + (0.3)(-0.2) + (0.3)(0.4) \\ &= 0.01 + 0.02 - 0.06 + 0.12 = 0.09 \\ z_2 &= (0.1)(0.5) + (0.1)(-0.2) + (0.3)(0.4) + (0.3)(0.3) \\ &= 0.05 - 0.02 + 0.12 + 0.09 = 0.24 \\ z_3 &= (0.1)(-0.3) + (0.1)(0.4) + (0.3)(0.1) + (0.3)(0.2) \\ &= -0.03 + 0.04 + 0.03 + 0.06 = 0.10 \\ z_4 &= (0.1)(0.3) + (0.1)(0.3) + (0.3)(-0.1) + (0.3)(0.5) \\ &= 0.03 + 0.03 - 0.03 + 0.15 = 0.18 \\ z_5 &= (0.1)(-0.2) + (0.1)(0.1) + (0.3)(0.5) + (0.3)(0.1) \\ &= -0.02 + 0.01 + 0.15 + 0.03 = 0.17 \\ z_6 &= (0.1)(0.4) + (0.1)(-0.3) + (0.3)(0.2) + (0.3)(0.1) \\ &= 0.04 - 0.03 + 0.06 + 0.03 = 0.10 \end{align*}\]Vetor de scores: $z = [0.09, 0.09, 0.24, 0.10, 0.18, 0.17, 0.10]$
-
Aplicar softmax para obter probabilidades: a função softmax transforma os scores em probabilidades. Usando o vetor $z$
\[z = [0.09, 0.09, 0.24, 0.10, 0.18, 0.17, 0.10]\]Calculando as exponenciais $e^{z_i}$:
\[\begin{align*} e^{0.09} &\approx 1.09417 \\ e^{0.09} &\approx 1.09417 \\ e^{0.24} &\approx 1.27125 \\ e^{0.10} &\approx 1.10517 \\ e^{0.18} &\approx 1.19722 \\ e^{0.17} &\approx 1.18530 \\ e^{0.10} &\approx 1.10517 \end{align*}\]Soma das exponenciais:
\[\sum_{j=0}^{6} e^{z_j} \approx 1.09417 + 1.09417 + 1.27125 + 1.10517 + 1.19722 + 1.18530 + 1.10517 \approx 8.05245\]Probabilidades após softmax:
\[\begin{align*} P(\text{o} \vert \text{contexto}) &= \frac{e^{0.09}}{\sum e^{z_j}} \approx \frac{1.09417}{8.05245} \approx 0.13588 \\ P(\text{gato} \vert \text{contexto}) &= \frac{e^{0.09}}{\sum e^{z_j}} \approx \frac{1.09417}{8.05245} \approx 0.13588 \\ P(\text{preto} \vert \text{contexto}) &= \frac{e^{0.24}}{\sum e^{z_j}} \approx \frac{1.27125}{8.05245} \approx 0.15787 \\ P(\text{corre} \vert \text{contexto}) &= \frac{e^{0.10}}{\sum e^{z_j}} \approx \frac{1.10517}{8.05245} \approx 0.13724 \\ P(\text{pelo} \vert \text{contexto}) &= \frac{e^{0.18}}{\sum e^{z_j}} \approx \frac{1.19722}{8.05245} \approx 0.14867 \\ P(\text{jardim} \vert \text{contexto}) &= \frac{e^{0.17}}{\sum e^{z_j}} \approx \frac{1.18530}{8.05245} \approx 0.14720 \\ P(\text{cachorro} \vert \text{contexto}) &= \frac{e^{0.10}}{\sum e^{z_j}} \approx \frac{1.10517}{8.05245} \approx 0.13724 \end{align*}\]Arredondando para 3 casas decimais, porque ninguém é de ferro, temos $P \approx [0.136, 0.136, 0.158, 0.137, 0.149, 0.147, 0.137]$. Note que a soma é $\approx 1.000$
-
Calcular a perda (erro): usando a probabilidade para a palavra-alvo
\[L = -\log(P(\text{preto} \vert \text{contexto})) \approx -\log(0.15787)\] \[L \approx -(-1.846) \approx 1.846\]preto($P(\text{preto} \vert \text{contexto}) \approx 0.15787$): -
Propagação do erro (Backpropagation): calculamos os gradientes $\frac{\partial L}{\partial z_j}$ usando as probabilidades:
Gradiente para a camada de saída: o gradiente do erro em relação aos scores $z$ é $e = P - y$, onde $P$ é o vetor de probabilidades calculado e $y$ é o vetor One-Hot da palavra-alvo
\[y = [0, 0, 1, 0, 0, 0, 0]\] \[P \approx [0.136, 0.136, 0.158, 0.137, 0.149, 0.147, 0.137]\] \[e = \frac{\partial L}{\partial z} = P - y \approx [0.136, 0.136, 0.158-1, 0.137, 0.149, 0.147, 0.137]\] \[e = \frac{\partial L}{\partial z} \approx [0.136, 0.136, -0.842, 0.137, 0.149, 0.147, 0.137]\]preto.Especificamente para $z_2$ (preto):
\[\frac{\partial L}{\partial z_2} = P(\text{preto} \vert \text{contexto}) - 1 \approx 0.15787 - 1 = -0.84213\]Para as outras palavras $j \neq 2$:
\[\frac{\partial L}{\partial z_j} = P(w_j \vert \text{contexto})\]Ex: $\frac{\partial L}{\partial z_1} = P(\text{gato} \vert \text{contexto}) \approx 0.13588$
Atualização dos pesos da matriz de saída: para atualizar a coluna de pesos correspondente à palavra-alvo
\[\Delta W_{\text{saída}, :, 2} = \eta \cdot \frac{\partial L}{\partial z_2} \cdot h^T\]preto(coluna de índice 2) na matriz $W_{\text{saída}}$, calculamos:Alternativamente, podemos trabalhar com a transposta de $W_{\text{saída}}$ e atualizar a linha 2:
\[\Delta (\text{linha } 2 \text{ de } W_{\text{saída}}^T) = \eta \cdot \frac{\partial L}{\partial z_2} \cdot h\]Assumindo $\eta = 0.01$:
\[\Delta W_{\text{saída},2}^T = 0.01 \cdot (-0.84213) \cdot [0.1, 0.1, 0.3, 0.3]\] \[\Delta W_{\text{saída},2}^T \approx -0.0084213 \cdot [0.1, 0.1, 0.3, 0.3]\] \[\Delta W_{\text{saída},2}^T \approx [-0.000842, -0.000842, -0.002526, -0.002526]\]Gradiente para a camada oculta: o gradiente do erro em relação à camada oculta $h$ é dado por:
\[\frac{\partial L}{\partial h} = e \cdot W_{\text{saída}}^T = \sum_{j=0}^{6} \frac{\partial L}{\partial z_j} \cdot (\text{linha } j \text{ de } W_{\text{saída}}^T)\] \[\frac{\partial L}{\partial h} = \frac{\partial L}{\partial z} \times W_{\text{saída}}^T\]onde $\frac{\partial L}{\partial z}$ é de dimensão $1 \times 7$ e $W_{\text{saída}}^T$ é de dimensão $7 \times 4$.
Este cálculo requer multiplicar o vetor de gradiente $e$ pela transposta de $W_{\text{saída}}$:
\[\begin{align*} \frac{\partial L}{\partial h} &\approx [0.136, 0.136, -0.842, 0.137, 0.149, 0.147, 0.137] \times \begin{bmatrix} 0.2 & 0.1 & 0.3 & -0.1 \\ 0.1 & 0.2 & -0.2 & 0.4 \\ 0.5 & -0.2 & 0.4 & 0.3 \\ -0.3 & 0.4 & 0.1 & 0.2 \\ 0.3 & 0.3 & -0.1 & 0.5 \\ -0.2 & 0.1 & 0.5 & 0.1 \\ 0.4 & -0.3 & 0.2 & 0.1 \end{bmatrix} \end{align*}\]Vamos calcular os dois primeiros elementos detalhadamente:
\[\begin{align*} \frac{\partial L}{\partial h_0} &= (0.136)(0.2) + (0.136)(0.1) + (-0.842)(0.5) + (0.137)(-0.3) + (0.149)(0.3) + (0.147)(-0.2) + (0.137)(0.4) \\ &= 0.0272 + 0.0136 - 0.4210 - 0.0411 + 0.0447 - 0.0294 + 0.0548 \\ &= -0.3512 \end{align*}\] \[\begin{align*} \frac{\partial L}{\partial h_1} &= (0.136)(0.1) + (0.136)(0.2) + (-0.842)(-0.2) + (0.137)(0.4) + (0.149)(0.3) + (0.147)(0.1) + (0.137)(-0.3) \\ &= 0.0136 + 0.0272 + 0.1684 + 0.0548 + 0.0447 + 0.0147 - 0.0411 \\ &= 0.2823 \end{align*}\]Calculando da mesma forma para os demais elementos, obtemos o vetor completo:
\[\frac{\partial L}{\partial h} \approx [-0.3512, 0.2823, −0.2235, −0.0815]\]Atualização dos vetores de embedding: O gradiente $\frac{\partial L}{\partial h}$ é distribuído igualmente para os vetores de embedding das palavras de contexto:
\[\frac{\partial L}{\partial v_{\text{gato}}} = \frac{\partial L}{\partial v_{\text{corre}}} = \frac{1}{2} \frac{\partial L}{\partial h}\] \[\Delta v_{\text{gato}} = \Delta v_{\text{corre}} = \frac{\eta}{2} \frac{\partial L}{\partial h}\]Atualização final: Os pesos e embeddings são atualizados usando a regra de gradiente descendente:
\[W_{\text{saída}}^{\text{new}} = W_{\text{saída}} - \eta \cdot h^T \cdot \frac{\partial L}{\partial z}\] \[v_{\text{gato}}^{\text{new}} = v_{\text{gato}} - \Delta v_{\text{gato}}\] \[v_{\text{corre}}^{\text{new}} = v_{\text{corre}} - \Delta v_{\text{corre}}\]
Nota sobre a Taxa de Aprendizado ($η$)
O símbolo $η$ (eta), presente nas fórmulas de atualização de pesos (como $W_{\text{saída}}^{\text{new}} = W_{\text{saída}} - \eta \cdot h^T \cdot \frac{\partial L}{\partial z}$), representa a Taxa de Aprendizado (ou Learning Rate).
No contexto do treinamento de modelos de machine learning como o Word2Vec (seja CBoW ou SkipGram), a Taxa de Aprendizado $η$, também representada como $α$, em alguns artigos, é um hiperparâmetro que controla o quão rápido o modelo aprende a partir do erro calculado. Mais especificamente:
Ajuste dos Pesos: durante o treinamento, o modelo calcula um erro, a diferença entre o que ele previu e o que era esperado. Esse erro é usado para calcular gradientes ($\frac{\partial L}{\partial \text{peso}}$), que indicam a direção na qual os pesos. Neste caso, os vetores de embedding de entrada $v_w$ e os pesos de saída $v’_w$ devem ser ajustados para minimizar o erro $L$.
Tamanho do Passo: a Taxa de Aprendizado $η$ determina o tamanho do “passo” que o modelo dá na direção indicada pelo gradiente ao atualizar esses pesos. A fórmula básica de atualização, usando gradiente descendente é:
\[\text{novo_peso} = \text{peso_antigo} - \eta \times \text{gradiente_do_erro}\]Um passo maior (maior $η$) significa uma atualização maior nos pesos a cada exemplo de treinamento.
Impacto do Valor de $η$: A escolha do valor correto para $η$ é fundamental para o sucesso do treinamento:
Taxa Alta ($0.1$, $0.5$): O modelo aprende mais rápido inicialmente, dá passos maiores, mas corre o risco de passar do ponto ótimo (chamamos isso de overshooting), podendo levar a instabilidade no treinamento, representada por oscilações grandes na função de perda, ou até mesmo divergir. O erro aumentar em vez de diminuir.
Taxa Baixa ($0.001$, $0.0001$): O modelo aprende mais devagar, dá passos menores, o que pode tornar o treinamento muito longo. Embora geralmente leve a uma convergência mais estável. Se, é claro, o valor for apropriado. Também aumenta a chance de o modelo ficar preso em mínimos locais da função de erro que não são a melhor solução global.
A escolha de um valor adequado para $η$ (como o $0.01$ assumido neste exemplo numérico, ou o $0.05$ usado no código C++ a seguir) muitas vezes requer experimentação. É comum também usar técnicas que ajustam $η$ dinamicamente durante o treinamento, começando com um valor maior e diminuindo-o ao longo das épocas. Efeito conhecido como decaimento da taxa de aprendizado ou learning rate decay, como poderá ser visto na função
trainCBOWdo código C++.
(Note que a atualização de $v$ na verdade atualiza as linhas correspondentes na matriz $W_{\text{entrada}}$).
Este exemplo ilustra um único passo de treinamento do algoritmo Continuous Bag-of-Words (CBoW) para a predição da palavra preto a partir das palavras de contexto gato e corre. O processo completo de treinamento envolveria repetir estes sete passos para cada um dos pares contexto-alvo identificados na frase de exemplo, atualizando gradualmente as matrizes de peso $W_{\text{entrada}}$ e $W_{\text{saída}}$ através de múltiplas épocas de treinamento. Com cada atualização, o modelo aprende a associar palavras que aparecem em contextos similares através da minimização da função de perda, resultando em vetores de embedding que capturam relações semânticas significativas. É importante notar que, embora tenhamos usado um exemplo simples com dimensão $d=4$ e um vocabulário limitado, na prática, modelos Word2Vec são treinados em corpus extensos com milhões de palavras, resultando em representações vetoriais densas e semanticamente ricas que servem como fundamento para aplicações modernas de processamento de linguagem natural.
Vantagens e Desvantagens do CBoW
| Vantagens | Desvantagens |
|---|---|
| É eficiente para palavras frequentes, pois suaviza o ruído tirando a média de vários contextos | A média dos vetores de contexto pode diluir informações específicas |
| Geralmente mais rápido de treinar que o SkipGram | Não trata tão bem palavras raras quanto o SkipGram |
| Bom para corpus menores |
Implementação do CBoW em C++
O código a seguir, em C++ 20 implementa de forma didática o modelo Continuous Bag-of-Words (CBoW) descrito anteriormente. Este código está aderente à abordagem teórica que utiliza a função Softmax completa para calcular as probabilidades da palavra-alvo a partir do vetor de contexto médio, além de medir os tempos de execução das etapas principais, construção de vocabulário e treinamento.
A curiosa leitora deve observar que neste código, não usei qualquer biblioteca de álgebra linear, como a Eigen ou a Armadillo, para facilitar a leitura e compreensão do código. Preferi pegar o touro a unha. O resultado é que o O código é auto-contido e não depende de bibliotecas externas, exceto as padrão do C++ 20 e, certamente, pode ser muito otimizado.
#include <iostream> ///< Para entrada e saída padrão (std::cout).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de sequências.
#include <string> ///< Para std::string, usado em palavras e mensagens.
#include <unordered_map> ///< Para std::unordered_map, usado no mapeamento de palavras.
#include <random> ///< Para geração de números aleatórios (std::mt19937).
#include <cmath> ///< Para funções matemáticas como std::exp, std::sqrt e std::log.
#include <fstream> ///< Para leitura/escrita de arquivos.
#include <algorithm> ///< Para std::sort e outras funções de manipulação.
#include <numeric> ///< Para std::accumulate e std::transform.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <limits> ///< Para std::numeric_limits.
#include <chrono> ///< Para medir o tempo de execução (std::chrono::high_resolution_clock).
#define NOMINMAX ///< o windows.h inclui macros mim e max que conflitam com a
///< biblioteca padrão este define impede a definição destas macros
#include <windows.h> ///< Para SetConsoleOutputCP e CP_UTF8 (específico do Windows)
// --- Constantes ---
/** @brief Valor máximo para a entrada da função sigmóide/exponencial para evitar overflow. */
const float MAX_EXP = 6.0f;
/**
* @struct Word
* @brief Estrutura para representar uma palavra, sua contagem e seus vetores no modelo Word2Vec (CBoW).
*/
struct Word {
std::string word; ///< A palavra em si.
std::vector<float> vector; ///< O vetor de embedding de ENTRADA da palavra (v_w).
long long count = 0; ///< Contagem de ocorrências no corpus, inicializada como 0.
};
/**
* @class Word2Vec_CBOW
* @brief Uma classe que implementa o modelo Word2Vec com Continuous Bag-of-Words (CBoW) e Softmax.
*
* Esta classe constrói embeddings de palavras a partir de um corpus de texto, utilizando
* a abordagem CBoW para prever uma palavra-alvo a partir de seu contexto.
* Utiliza a função Softmax completa para o cálculo de probabilidades, aderindo ao
* exemplo teórico detalhado. Suporta treinamento, salvamento/carregamento de embeddings,
* busca de palavras similares e operações de analogia vetorial.
*/
class Word2Vec_CBOW {
private:
// --- Parâmetros do Modelo ---
int vector_size; ///< Dimensão dos vetores de embedding (d).
int window_size; ///< Tamanho máximo da janela de contexto (c).
float learning_rate; ///< Taxa de aprendizado inicial (eta).
// --- Vocabulário e Embeddings ---
std::unordered_map<std::string, int> word_to_index; ///< Mapeamento palavra -> índice.
std::vector<Word> vocabulary; ///< Lista de palavras e seus embeddings DE ENTRADA (matriz W_entrada).
std::vector<std::vector<float>> output_weights; ///< Matriz de pesos de SAÍDA (W_saida), output_weights[vocab_idx] -> v'_w.
// --- Contagens e Aleatoriedade ---
long long total_words; ///< Total de palavras no corpus.
mutable std::mt19937 rng; ///< Gerador Mersenne Twister (mutável para operações const como findSimilar).
std::uniform_int_distribution<int> uniform_window; ///< Distribuição para tamanho dinâmico da janela.
/**
* @brief Inicializa os embeddings de entrada e os pesos de saída com valores aleatórios.
*
* Os vetores são inicializados com valores pequenos aleatórios seguindo uma distribuição uniforme,
* conforme prática comum para facilitar a convergência durante o treinamento.
*/
void initializeEmbeddings() {
std::uniform_real_distribution<float> dist(-0.5f / vector_size, 0.5f / vector_size);
output_weights.resize(vocabulary.size(), std::vector<float>(vector_size));
for (size_t i = 0; i < vocabulary.size(); ++i) {
vocabulary[i].vector.resize(vector_size);
for (int j = 0; j < vector_size; ++j) {
vocabulary[i].vector[j] = dist(rng); // Inicializa embedding de entrada v_w
output_weights[i][j] = dist(rng); // Inicializa pesos de saída v'_w (poderia ser inicializado com zeros também)
}
}
std::cout << "Embeddings de entrada e pesos de saída inicializados para " << vocabulary.size() << " palavras.\n";
}
/**
* @brief Calcula a função Softmax para um vetor de scores.
* @param scores Vetor de scores (z) para cada palavra no vocabulário.
* @return Vetor de probabilidades (P) após aplicar Softmax.
* @note Inclui tratamento para evitar overflow numérico com exponenciais grandes.
*/
std::vector<float> softmax(const std::vector<float>& scores) const {
std::vector<float> probabilities(scores.size());
float max_score = -std::numeric_limits<float>::infinity();
for (float score : scores) {
if (score > max_score) {
max_score = score;
}
}
float sum_exp = 0.0f;
for (size_t i = 0; i < scores.size(); ++i) {
// Subtrai max_score para estabilidade numérica
float exp_val = std::exp(scores[i] - max_score);
probabilities[i] = exp_val;
sum_exp += exp_val;
}
if (sum_exp > 0.0f) { // Evita divisão por zero
for (size_t i = 0; i < probabilities.size(); ++i) {
probabilities[i] /= sum_exp;
}
}
return probabilities;
}
/**
* @brief Treina o modelo para um único par (contexto -> alvo) usando CBoW e Softmax.
*
* Implementa os passos descritos no exemplo CBoW do arquivo:
* 1. Calcula o vetor médio do contexto (h).
* 2. Calcula os scores (z) para todas as palavras do vocabulário.
* 3. Aplica Softmax para obter probabilidades (P).
* 4. Calcula o erro (gradiente) para a camada de saída (e = P - y).
* 5. Propaga o erro para atualizar os pesos de saída (W_saida).
* 6. Propaga o erro para atualizar os embeddings de entrada das palavras de contexto (W_entrada).
*
* @param context_indices Vetor contendo os índices das palavras de contexto.
* @param target_idx Índice da palavra-alvo a ser prevista.
*/
void trainCBOWPair(const std::vector<int>& context_indices, int target_idx) {
if (context_indices.empty()) {
return; // Não há contexto para treinar
}
// --- Passo 1 & 2: Calcular vetor médio do contexto (h) ---
std::vector<float> h(vector_size, 0.0f);
for (int context_idx : context_indices) {
const auto& context_vector = vocabulary[context_idx].vector;
for (int i = 0; i < vector_size; ++i) {
h[i] += context_vector[i];
}
}
// Calcular a média dividindo pelo número de palavras no contexto
float num_context_words = static_cast<float>(context_indices.size());
for (int i = 0; i < vector_size; ++i) {
h[i] /= num_context_words;
}
// --- Passo 4: Calcular scores (z = h * W_saida) ---
// z_j = h . v'_j (produto escalar de h com o vetor de SAÍDA da palavra j)
std::vector<float> scores(vocabulary.size());
for (size_t j = 0; j < vocabulary.size(); ++j) {
float dot_product = 0.0f;
for (int i = 0; i < vector_size; ++i) {
dot_product += h[i] * output_weights[j][i]; // h . v'_j
}
scores[j] = dot_product;
}
// --- Passo 5: Aplicar Softmax para obter probabilidades (P) ---
std::vector<float> probabilities = softmax(scores);
// --- Passo 7: Backpropagation ---
// Calcular erro na camada de saída (e = P - y)
// y é o vetor One-Hot da palavra alvo (target_idx)
std::vector<float> error_output_layer = probabilities; // Copia P
error_output_layer[target_idx] -= 1.0f; // Subtrai 1 na posição do alvo (P - y)
// Calcular gradiente para a camada oculta (dL/dh = e * W_saida^T)
// dL/dh_i = sum_j (e_j * W_saida[j][i]) = sum_j (e_j * v'_j[i])
std::vector<float> gradient_hidden_layer(vector_size, 0.0f);
for (int i = 0; i < vector_size; ++i) { // Para cada dimensão do embedding
float sum = 0.0f;
for (size_t j = 0; j < vocabulary.size(); ++j) { // Somar sobre todas as palavras do vocabulário
sum += error_output_layer[j] * output_weights[j][i];
}
gradient_hidden_layer[i] = sum;
}
// --- Atualizar Pesos ---
// Atualizar pesos de SAÍDA (W_saida)
// dL/dW_saida[j] = dL/dz_j * dz_j/dW_saida[j] = e_j * h
// v'_j (novo) = v'_j (antigo) - eta * e_j * h
for (size_t j = 0; j < vocabulary.size(); ++j) {
float error_j = error_output_layer[j]; // e_j
for (int i = 0; i < vector_size; ++i) {
output_weights[j][i] -= learning_rate * error_j * h[i];
}
}
// Atualizar embeddings de ENTRADA (W_entrada) das palavras de contexto
// dL/dv_context = dL/dh * dh/dv_context = dL/dh * (1 / num_context_words)
// v_context (novo) = v_context (antigo) - eta * (1 / num_context_words) * dL/dh
float factor = learning_rate / num_context_words;
for (int context_idx : context_indices) {
for (int i = 0; i < vector_size; ++i) {
vocabulary[context_idx].vector[i] -= factor * gradient_hidden_layer[i];
}
}
}
public:
/**
* @brief Construtor que inicializa os parâmetros do modelo CBoW.
* @param vector_size Dimensão dos vetores de embedding (padrão: 100).
* @param window_size Tamanho máximo da janela de contexto (padrão: 5).
* @param learning_rate Taxa de aprendizado inicial (padrão: 0.05 para CBoW com Softmax).
*/
Word2Vec_CBOW(int vector_size = 100, int window_size = 5, float learning_rate = 0.05f)
: vector_size(vector_size), window_size(window_size),
learning_rate(learning_rate), total_words(0), rng(std::random_device{}()) {
uniform_window = std::uniform_int_distribution<int>(1, window_size); // Janela dinâmica [1, window_size]
std::cout << "Modelo Word2Vec CBoW inicializado.\n";
std::cout << " Dimensão Vetores (d): " << vector_size << "\n";
std::cout << " Tamanho Janela (c): " << window_size << "\n";
std::cout << " Taxa Aprendizado (eta): " << learning_rate << "\n";
}
/**
* @brief Constrói o vocabulário a partir de um corpus de texto.
*
* Conta as ocorrências de cada palavra e mapeia palavras para índices.
* Após construir o vocabulário, inicializa os embeddings.
*
* @param corpus Vetor de sentenças, onde cada sentença é um vetor de palavras (strings).
*/
void buildVocabulary(const std::vector<std::vector<std::string>>& corpus) {
std::cout << "Construindo vocabulário...\n";
std::unordered_map<std::string, long long> word_counts;
total_words = 0;
// Contar ocorrências
for (const auto& sentence : corpus) {
for (const auto& word : sentence) {
word_counts[word]++;
total_words++;
}
}
// Verificar se o corpus é válido
if (word_counts.empty()) {
std::cerr << "Erro: Corpus vazio ou inválido. Vocabulário não pode ser construído.\n";
return;
}
std::cout << " Total de palavras no corpus: " << total_words << "\n";
std::cout << " Número de palavras únicas: " << word_counts.size() << "\n";
// Construir vocabulário
vocabulary.clear();
word_to_index.clear();
int index = 0;
// Poderíamos adicionar filtragem por frequência mínima aqui se necessário
for (const auto& [word, count] : word_counts) {
Word w;
w.word = word;
w.count = count;
vocabulary.push_back(w);
word_to_index[word] = index++;
}
// Inicializar embeddings de entrada e pesos de saída
initializeEmbeddings();
std::cout << "Vocabulário construído e embeddings inicializados.\n";
}
/**
* @brief Treina o modelo CBoW com Softmax completo.
*
* Itera sobre o corpus por um número definido de épocas. Em cada época,
* processa cada palavra, define seu contexto e chama `trainCBOWPair`
* para ajustar os embeddings e pesos. A taxa de aprendizado diminui linearmente
* ao longo das épocas.
*
* @param corpus Vetor de sentenças para treinamento.
* @param epochs Número de épocas de treinamento (padrão: 15).
*/
void trainCBOW(const std::vector<std::vector<std::string>>& corpus, int epochs = 15) {
if (vocabulary.empty()) {
std::cerr << "Erro: Vocabulário não inicializado. Execute buildVocabulary primeiro.\n";
return;
}
std::cout << "Iniciando treinamento CBoW por " << epochs << " épocas...\n";
float initial_lr = learning_rate;
long long words_processed_epoch = 0; // Para acompanhar progresso se necessário
for (int epoch = 0; epoch < epochs; ++epoch) {
words_processed_epoch = 0;
long long pairs_trained = 0;
for (const auto& sentence : corpus) {
for (size_t i = 0; i < sentence.size(); ++i) {
// Encontrar índice da palavra-alvo
auto target_it = word_to_index.find(sentence[i]);
if (target_it == word_to_index.end()) continue; // Palavra fora do vocabulário
int target_idx = target_it->second;
// Determinar janela de contexto dinâmica
int current_window = uniform_window(rng);
std::vector<int> context_indices;
context_indices.reserve(static_cast<size_t>(window_size) * 2);
// Coletar índices das palavras de contexto
for (int j = -current_window; j <= current_window; ++j) {
if (j == 0) continue; // Pular a palavra-alvo
size_t context_pos = i + j;
// Verificar limites da sentença
if (context_pos < sentence.size()) { // size_t é sempre >= 0
auto context_it = word_to_index.find(sentence[context_pos]);
if (context_it != word_to_index.end()) {
context_indices.push_back(context_it->second);
}
}
}
// Treinar o par se houver contexto
if (!context_indices.empty()) {
trainCBOWPair(context_indices, target_idx);
pairs_trained++;
}
words_processed_epoch++;
} // Fim do loop da sentença
} // Fim do loop do corpus
// Ajustar taxa de aprendizado linearmente
learning_rate = initial_lr * (1.0f - static_cast<float>(epoch + 1) / epochs);
// Garantir que a taxa de aprendizado não seja menor que um valor mínimo (opcional)
learning_rate = std::max(learning_rate, initial_lr * 0.0001f);
std::cout << " Época " << epoch + 1 << "/" << epochs << " completa. Pares treinados: " << pairs_trained
<< ". LR atual: " << std::fixed << std::setprecision(6) << learning_rate << "\n";
} // Fim do loop das épocas
std::cout << "Treinamento CBoW concluído.\n";
}
/**
* @brief Salva os embeddings de ENTRADA em um arquivo no formato texto Word2Vec.
* @param filename Nome do arquivo de saída.
* @note Salva apenas os vetores de entrada (v_w), que são tipicamente usados como embeddings.
*/
void saveEmbeddings(const std::string& filename) const {
std::cout << "Salvando embeddings de entrada em " << filename << "...\n";
std::ofstream file(filename);
if (!file.is_open()) {
std::cerr << "Erro ao abrir arquivo para escrita: " << filename << "\n";
return;
}
// Cabeçalho: número_de_palavras dimensão_vetor
file << vocabulary.size() << " " << vector_size << "\n";
// Linhas: palavra val1 val2 ... valN
for (const auto& word : vocabulary) {
file << word.word;
for (float val : word.vector) {
file << " " << std::fixed << std::setprecision(6) << val;
}
file << "\n";
}
file.close();
std::cout << "Embeddings salvos com sucesso.\n";
}
/**
* @brief Carrega embeddings pré-treinados de um arquivo.
* @param filename Nome do arquivo de entrada.
* @return True se o carregamento for bem-sucedido, false caso contrário.
* @note Assume formato texto Word2Vec. Inicializa pesos de saída aleatoriamente
* se for carregar embeddings para continuar o treinamento.
*/
bool loadEmbeddings(const std::string& filename) {
std::cout << "Carregando embeddings de " << filename << "...\n";
std::ifstream file(filename);
if (!file.is_open()) {
std::cerr << "Erro ao abrir arquivo para leitura: " << filename << "\n";
return false;
}
size_t vocab_size;
int loaded_vector_size;
file >> vocab_size >> loaded_vector_size;
// Verifica se a dimensão do vetor carregado corresponde à configuração do modelo
if (file.fail() || loaded_vector_size <= 0) {
std::cerr << "Erro ao ler cabeçalho do arquivo: " << filename << "\n";
return false;
}
std::cout << " Arquivo contém " << vocab_size << " palavras com dimensão " << loaded_vector_size << ".\n";
// Permite carregar embeddings com dimensão diferente, ajustando o modelo
// Ou pode gerar um erro se as dimensões não baterem, dependendo do caso de uso.
// Aqui, vamos ajustar o modelo para a dimensão carregada.
if (loaded_vector_size != vector_size) {
std::cout << " Aviso: Dimensão do vetor no arquivo (" << loaded_vector_size
<< ") difere da configuração do modelo (" << vector_size
<< "). Ajustando modelo para " << loaded_vector_size << ".\n";
vector_size = loaded_vector_size;
}
vocabulary.clear();
word_to_index.clear();
vocabulary.reserve(vocab_size);
for (size_t i = 0; i < vocab_size; ++i) {
Word w;
file >> w.word;
if (file.fail()) {
std::cerr << "Erro ao ler palavra no índice " << i << " do arquivo.\n";
return false; // Falha na leitura da palavra
}
w.vector.resize(vector_size);
for (int j = 0; j < vector_size; ++j) {
file >> w.vector[j];
if (file.fail()) {
std::cerr << "Erro ao ler valor do vetor para a palavra '" << w.word << "' no índice " << j << ".\n";
return false; // Falha na leitura do vetor
}
}
w.count = 1; // Contagem desconhecida ao carregar, definir como 1
vocabulary.push_back(w);
word_to_index[w.word] = i;
}
file.close();
// Se carregou embeddings, precisa inicializar os pesos de saída se for treinar mais
// Ou pode deixá-los vazios se for usar apenas para consulta.
// Vamos inicializá-los para permitir treinamento adicional.
output_weights.resize(vocabulary.size(), std::vector<float>(vector_size));
std::uniform_real_distribution<float> dist(-0.5f / vector_size, 0.5f / vector_size);
for (size_t i = 0; i < vocabulary.size(); ++i) {
for (int j = 0; j < vector_size; ++j) {
output_weights[i][j] = dist(rng);
}
}
total_words = vocabulary.size(); // Estimativa grosseira se não tivermos o corpus original
std::cout << "Embeddings carregados e pesos de saída (re)inicializados com sucesso.\n";
return true;
}
/**
* @brief Encontra as palavras com maior grau de similaridade a uma palavra dada usando similaridade de cosseno.
* @param word Palavra de consulta.
* @param top_n Número de palavras similares a retornar (padrão: 10).
* @return Vetor de pares (palavra, similaridade), ordenado por similaridade decrescente.
* @note Usa os embeddings de ENTRADA (v_w) para calcular a similaridade.
*/
std::vector<std::pair<std::string, float>> findSimilar(const std::string& word, int top_n = 10) const {
auto it = word_to_index.find(word);
if (it == word_to_index.end()) {
std::cerr << "Aviso: Palavra '" << word << "' não encontrada no vocabulário para busca de similaridade.\n";
return {};
}
int word_idx = it->second;
const auto& word_vector = vocabulary[word_idx].vector; // Usa vetor de ENTRADA
std::vector<std::pair<std::string, float>> similarities;
similarities.reserve(vocabulary.size());
for (size_t i = 0; i < vocabulary.size(); ++i) {
if (i == word_idx) continue; // Não comparar a palavra consigo mesma
float similarity = cosineSimilarity(word_vector, vocabulary[i].vector); // Compara vetores de ENTRADA
similarities.emplace_back(vocabulary[i].word, similarity);
}
// Ordenar por similaridade decrescente
std::sort(similarities.begin(), similarities.end(),
[](const auto& a, const auto& b) { return a.second > b.second; });
// Retornar os top_n resultados
if (similarities.size() > static_cast<size_t>(top_n)) {
similarities.resize(top_n);
}
return similarities;
}
/**
* @brief Calcula a similaridade de cosseno entre dois vetores.
* @param a Primeiro vetor.
* @param b Segundo vetor.
* @return Valor da similaridade de cosseno [-1, 1]. Retorna 0 se uma das normas for zero.
*/
float cosineSimilarity(const std::vector<float>& a, const std::vector<float>& b) const {
if (a.size() != b.size() || a.empty()) {
return 0.0f; // Vetores incompatíveis ou vazios
}
float dot_product = 0.0f;
float norm_a = 0.0f;
float norm_b = 0.0f;
for (size_t i = 0; i < a.size(); ++i) {
dot_product += a[i] * b[i];
norm_a += a[i] * a[i];
norm_b += b[i] * b[i];
}
// Evitar divisão por zero se um vetor for nulo
if (norm_a <= 0.0f || norm_b <= 0.0f) {
return 0.0f;
}
return dot_product / (std::sqrt(norm_a) * std::sqrt(norm_b));
}
/**
* @brief Realiza operações de analogia vetorial (a - b + c ≈ ?).
*
* Calcula o vetor resultante `vec(a) - vec(b) + vec(c)` e encontra as palavras
* cujos vetores de embedding (de entrada) são mais próximos a ele via similaridade de cosseno.
*
* @param a Primeira palavra positiva.
* @param b Palavra negativa.
* @param c Segunda palavra positiva.
* @param top_n Número de resultados a retornar (padrão: 5).
* @return Vetor de pares (palavra, similaridade).
*/
std::vector<std::pair<std::string, float>> analogy(const std::string& a,
const std::string& b,
const std::string& c,
int top_n = 5) const {
auto it_a = word_to_index.find(a);
auto it_b = word_to_index.find(b);
auto it_c = word_to_index.find(c);
if (it_a == word_to_index.end() || it_b == word_to_index.end() || it_c == word_to_index.end()) {
std::cerr << "Aviso: Uma ou mais palavras da analogia (" << a << ", " << b << ", " << c << ") não encontradas no vocabulário.\n";
return {};
}
const auto& vec_a = vocabulary[it_a->second].vector; // Vetor de ENTRADA
const auto& vec_b = vocabulary[it_b->second].vector; // Vetor de ENTRADA
const auto& vec_c = vocabulary[it_c->second].vector; // Vetor de ENTRADA
std::vector<float> result_vec(vector_size);
for (int i = 0; i < vector_size; ++i) {
result_vec[i] = vec_a[i] - vec_b[i] + vec_c[i];
}
// Normalizar o vetor resultante (opcional, mas comum)
float norm = 0.0f;
for (float val : result_vec) {
norm += val * val;
}
norm = std::sqrt(norm);
if (norm > 0.0f) {
for (float& val : result_vec) {
val /= norm;
}
}
// Encontrar palavras com maior grau de similaridades ao vetor resultante
std::vector<std::pair<std::string, float>> similarities;
similarities.reserve(vocabulary.size());
for (size_t i = 0; i < vocabulary.size(); ++i) {
// Não incluir as palavras de entrada na lista de resultados
if (vocabulary[i].word == a || vocabulary[i].word == b || vocabulary[i].word == c) {
continue;
}
float similarity = cosineSimilarity(result_vec, vocabulary[i].vector); // Compara com vetores de ENTRADA
similarities.emplace_back(vocabulary[i].word, similarity);
}
// Ordenar e retornar top_n
std::sort(similarities.begin(), similarities.end(),
[](const auto& x, const auto& y) { return x.second > y.second; });
if (similarities.size() > static_cast<size_t>(top_n)) {
similarities.resize(top_n);
}
return similarities;
}
/**
* @brief Retorna o vetor embedding de ENTRADA de uma palavra.
* @param word Palavra de consulta.
* @return Vetor de embedding (v_w). Retorna um vetor de zeros se a palavra não for encontrada.
*/
std::vector<float> getWordVector(const std::string& word) const {
auto it = word_to_index.find(word);
if (it == word_to_index.end()) {
std::cerr << "Aviso: Palavra '" << word << "' não encontrada no vocabulário para getWordVector.\n";
return std::vector<float>(vector_size, 0.0f);
}
return vocabulary[it->second].vector; // Retorna vetor de ENTRADA
}
};
/**
* @brief Função principal que demonstra o uso da classe Word2Vec_CBOW.
*
* Este programa cria um modelo Word2Vec CBoW, constrói o vocabulário a partir de um corpus
* simplificado, treina o modelo com CBoW e Softmax completo, e demonstra funcionalidades
* como busca de palavras similares, operações de analogia e salvamento de embeddings.
*
* @return 0 em caso de execução bem-sucedida.
*/
/**
* @brief Função principal que demonstra o uso da classe Word2Vec_CBOW.
*
* Este programa cria um modelo Word2Vec CBoW, constrói o vocabulário a partir de um corpus
* simplificado, treina o modelo com CBoW e Softmax completo, e demonstra funcionalidades
* como busca de palavras similares, operações de analogia e salvamento de embeddings.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
// Configurar o console para UTF-8 (Específico do Windows)
// Em outros sistemas (Linux/macOS), isso geralmente não é necessário
// se o terminal já estiver configurado para UTF-8.
#ifdef _WIN32
SetConsoleOutputCP(CP_UTF8);
std::cout << "Console configurado para UTF-8.\n";
#endif
// Corpus simplificado (o mesmo do exemplo anterior)
std::vector<std::vector<std::string>> corpus = {
{"o", "gato", "preto", "corre", "pelo", "jardim"},
{"o", "cachorro", "late", "para", "o", "gato"},
{"gatos", "e", "cachorros", "são", "animais", "domésticos"},
{"muitas", "pessoas", "gostam", "de", "ter", "um", "animal", "de", "estimação"},
{"os", "gatos", "gostam", "de", "dormir", "durante", "o", "dia"},
{"os", "cachorros", "precisam", "passear", "todos", "os", "dias"}
};
std::cout << "Corpus de exemplo carregado com " << corpus.size() << " sentenças.\n";
// --- Criar e Treinar Modelo CBoW ---
// Usar parâmetros menores para o exemplo pequeno: dimensão 20, janela 2, lr 0.05
// Softmax completo é mais sensível à taxa de aprendizado e requer mais épocas.
Word2Vec_CBOW model(20, 2, 0.05f);
// Medir Construção do Vocabulário
auto start_vocab = std::chrono::high_resolution_clock::now();
// Calcular o tempo de construção do vocabulário
auto end_vocab = std::chrono::high_resolution_clock::now();
auto duration_vocab = std::chrono::duration_cast<std::chrono::nanoseconds>(end_vocab - start_vocab);
std::cout << "Tempo de construção do vocabulário: " << duration_vocab.count() << " ns\n";
// Medir Treinamento
int epochs_count = 100;
auto start_train = std::chrono::high_resolution_clock::now();
// Construir vocabulário a partir do corpus
model.buildVocabulary(corpus);
// Treinar o modelo CBoW (pode precisar de mais épocas que SkipGram/NegSampling)
model.trainCBOW(corpus, 100); // Aumentar épocas para CBoW com Softmax
auto end_train = std::chrono::high_resolution_clock::now();
auto duration_train = std::chrono::duration_cast<std::chrono::nanoseconds>(end_train - start_train);
std::cout << "Tempo de treinamento (" << epochs_count << " épocas): " << duration_train.count() << " ns\n";
// --- FIM ADIÇÃO ---
// --- Usar o Modelo Treinado ---
// Encontrar palavras similares a 'gato'
std::cout << "\n--- Palavras similares a 'gato' ---\n";
auto similar_to_cat = model.findSimilar("gato", 5); // Top 5
if (similar_to_cat.empty()) {
std::cout << "Nenhuma palavra similar encontrada (ou 'gato' não está no vocabulário).\n";
}
else {
for (const auto& [word, similarity] : similar_to_cat) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
}
}
// Encontrar palavras similares a 'cachorro'
std::cout << "\n--- Palavras similares a 'cachorro' ---\n";
auto similar_to_dog = model.findSimilar("cachorro", 5); // Top 5
if (similar_to_dog.empty()) {
std::cout << "Nenhuma palavra similar encontrada (ou 'cachorro' não está no vocabulário).\n";
}
else {
for (const auto& [word, similarity] : similar_to_dog) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
}
}
// Testar analogia: gato - gatos + cachorro ≈ cachorros ?
// (Funciona melhor com corpus maiores e embeddings bem treinados)
std::cout << "\n--- Analogia: gato está para gatos assim como cachorro está para...? ---\n";
auto analogy_results = model.analogy("gato", "gatos", "cachorro", 3); // Top 3
if (analogy_results.empty()) {
std::cout << "Não foi possível calcular a analogia (palavras ausentes ou vocabulário pequeno).\n";
}
else {
for (const auto& [word, similarity] : analogy_results) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
}
// Esperado: 'cachorros' se o treino foi bom o suficiente
}
// Obter vetor de uma palavra específica
std::cout << "\n--- Vetor da palavra 'animal' ---\n";
std::vector<float> vec_animal = model.getWordVector("animal");
if (vec_animal != std::vector<float>(20, 0.0f)) { // Compara com vetor de zeros
std::cout << " ["; // <--- CORRIGIDO AQUI (adicionado ';')
for (size_t i = 0; i < vec_animal.size(); ++i) {
std::cout << std::fixed << std::setprecision(3) << vec_animal[i] << (i == vec_animal.size() - 1 ? "" : ", ");
}
std::cout << "]\n";
}
// Salvar os embeddings de entrada resultantes
model.saveEmbeddings("cbow_word_embeddings.txt");
// Exemplo de como carregar embeddings (opcional)
// Word2Vec_CBOW loaded_model(20); // Cria modelo com a dimensão correta
// if (loaded_model.loadEmbeddings("cbow_word_embeddings.txt")) {
// std::cout << "\nEmbeddings carregados com sucesso no modelo 'loaded_model'.\n";
// auto similar_loaded = loaded_model.findSimilar("gato", 3);
// std::cout << "Palavras similares a 'gato' (modelo carregado):\n";
// for (const auto& [word, similarity] : similar_loaded) {
// std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
// }
// } else {
// std::cerr << "Falha ao carregar embeddings.\n";
// }
std::cout << "\nExecução concluída.\n";
return 0;
}
SkipGram: Prevendo o Contexto a partir da Palavra
O modelo SkipGram inverte a tarefa do CBoW: em vez de usar o contexto para prever a palavra-alvo, usa a palavra-alvo para prever cada palavra do contexto. Esta inversão na direção da previsão, apesar de sutil, produz resultados diferentes, muito diferentes, para palavras raras.
No SkipGram, para cada palavra-alvo, tentamos prever cada uma das palavras do contexto separadamente. O próprio nome Skip-gram refere-se ao fato de que o modelo considera N-grams com lacunas,skips em inglês, entre as palavras.
Dada uma sequência de palavras de treinamento $w_1, w_2, …, w_T$, o objetivo é maximizar a log-probabilidade:
\[\frac{1}{T} \sum_{t=1}^{T} \sum_{-c \leq j \leq c, j \neq 0} \log p(w_{t+j} \vert w_t)\]Neste caso:
- $c$ é o tamanho da janela de contexto;
-
$p(w_{t+j} \vert w_t)$ é calculado usando softmax:
\[p(w_O \vert w_I) = \frac{\exp(v'_{w_O}v_{w_I})}{\sum_{w \in V} \exp(v'_{w}v_{w_I})}\]
Aqui, $w_I$ representa a palavra de entrada, a palavra alvo, e $w_O$ a palavra de saída, o contexto.
A arquitetura específica do SkipGram é composta por:
- Entradas: um vetor One-Hot para a palavra-alvo;
- Projeção: o vetor é projetado para a camada oculta (embedding);
- Saída: múltiplos softmax, um para cada posição de contexto, prevendo a palavra naquela posição.
Na implementação original (Mikolov et al, 2013), em vez de múltiplos softmax na camada de saída, cada par palavra-alvo/palavra-contexto é tratado como um exemplo de treinamento individual, o que simplifica a computação. A Figura 5 ilustra a arquitetura do modelo SkipGram.
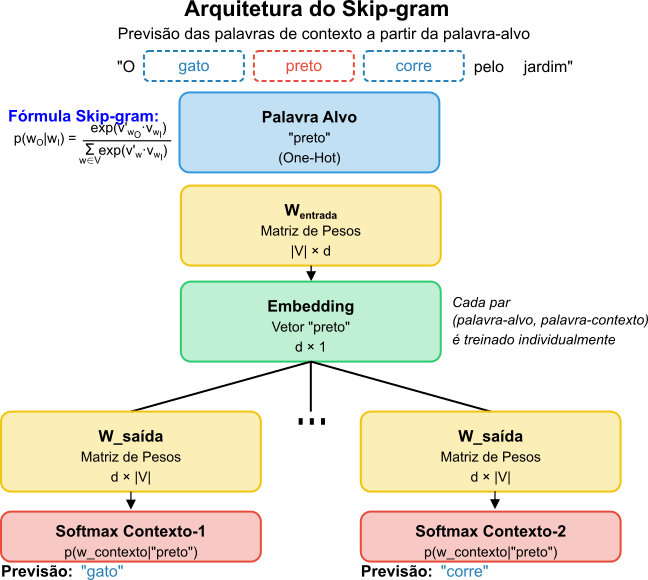
Figura 5: Arquitetura do modelo SkipGram que prevê as palavras do contexto a partir da palavra-alvo. O diagrama mostra como o vetor One-Hot da palavra-alvo é transformado em um embedding denso através da matriz de pesos compartilhada, e então utilizado para prever cada palavra de contexto através de uma função softmax independente para cada posição no contexto.
Exemplo de Treinamento com SkipGram
Para ilustrar o processo de treinamento do SkipGram, consideremos novamente a frase de exemplo:
$D_1$ = O gato preto corre pelo jardim
Com uma janela de tamanho $1$, o SkipGram geraria os seguintes pares alvo-contexto:
O→ [gato];gato→ [O,preto];preto→ [gato,corre];corre→ [preto,pelo];pelo→ [corre,jardim];jardim→ [pelo].
Note a diferença fundamental em relação ao CBoW: enquanto o CBoW usa múltiplas palavras de contexto para prever uma única palavra-alvo, o SkipGram usa uma única palavra-alvo para prever múltiplas palavras de contexto. Cada palavra-alvo gera tantos exemplos de treinamento quanto o número de palavras em seu contexto.
Vamos detalhar o processo de treinamento para o exemplo $3$, onde a palavra-alvo preto é usada para prever as palavras de contexto gato e corre:
-
Converter a palavra-alvo em vetor One-Hot: Considerando o mesmo vocabulário do exemplo que usamos para o CBoW:
\[V = \{\text{o}, \text{gato}, \text{preto}, \text{corre}, \text{pelo}, \text{jardim}, \text{cachorro}\}\]com $\vert V \vert = 7$. O vetor One-Hot para
\[\text{preto} = [0, 0, 1, 0, 0, 0, 0]\]pretoserá dado por: -
Projetar para obter o vetor de embedding: Com a mesma dimensão de embedding $d = 4$ e a matriz $W_{\text{entrada}}$ de dimensão $\vert V \vert \times d = 7 \times 4$:
\[W_{\text{entrada}} = \begin{bmatrix} 0.1 & 0.2 & -0.1 & 0.3 \\ 0.2 & -0.4 & 0.7 & -0.2 \\ 0.4 & -0.3 & 0.1 & 0.5 \\ 0.0 & 0.6 & -0.1 & 0.8 \\ -0.3 & 0.2 & -0.5 & -0.5 \\ 0.5 & 0.1 & 0.3 & -0.2 \\ 0.1 & -0.3 & 0.8 & -0.1 \end{bmatrix}\]O vetor de embedding para
\[v_{\text{preto}} = [0, 0, 1, 0, 0, 0, 0] \times W_{\text{entrada}} = [0.4, -0.3, 0.1, 0.5]\]pretoé obtido multiplicando seu vetor One-Hot pela matriz $W_{\text{entrada}}$: -
Calcular scores para todas as palavras do vocabulário: Para cada palavra de contexto (neste caso,
\[W_{\text{saída}} = \begin{bmatrix} 0.2 & 0.1 & 0.5 & -0.3 & 0.3 & -0.2 & 0.4 \\ 0.1 & 0.2 & -0.2 & 0.4 & 0.3 & 0.1 & -0.3 \\ 0.3 & -0.2 & 0.4 & 0.1 & -0.1 & 0.5 & 0.2 \\ -0.1 & 0.4 & 0.3 & 0.2 & 0.5 & 0.1 & 0.1 \end{bmatrix}\]gatoecorre), calculamos o produto escalar do vetor de embedding da palavra-alvo com cada linha da matriz $W_{\text{saída}}$:Calculamos $z = v_{\text{preto}} \times W_{\text{saída}}$:
\[\begin{align*} z_0 &= (0.4)(0.2) + (-0.3)(0.1) + (0.1)(0.3) + (0.5)(-0.1) \\ &= 0.08 - 0.03 + 0.03 - 0.05 = 0.03 \\ z_1 &= (0.4)(0.1) + (-0.3)(0.2) + (0.1)(-0.2) + (0.5)(0.4) \\ &= 0.04 - 0.06 - 0.02 + 0.20 = 0.16 \\ z_2 &= (0.4)(0.5) + (-0.3)(-0.2) + (0.1)(0.4) + (0.5)(0.3) \\ &= 0.20 + 0.06 + 0.04 + 0.15 = 0.45 \\ z_3 &= (0.4)(-0.3) + (-0.3)(0.4) + (0.1)(0.1) + (0.5)(0.2) \\ &= -0.12 - 0.12 + 0.01 + 0.10 = -0.13 \\ z_4 &= (0.4)(0.3) + (-0.3)(0.3) + (0.1)(-0.1) + (0.5)(0.5) \\ &= 0.12 - 0.09 - 0.01 + 0.25 = 0.27 \\ z_5 &= (0.4)(-0.2) + (-0.3)(0.1) + (0.1)(0.5) + (0.5)(0.1) \\ &= -0.08 - 0.03 + 0.05 + 0.05 = -0.01 \\ z_6 &= (0.4)(0.4) + (-0.3)(-0.3) + (0.1)(0.2) + (0.5)(0.1) \\ &= 0.16 + 0.09 + 0.02 + 0.05 = 0.32 \end{align*}\]Vetor de scores: $z = [0.03, 0.16, 0.45, -0.13, 0.27, -0.01, 0.32]$
-
Aplicar softmax para obter probabilidades: A função softmax transforma os scores em probabilidades:
\[\begin{align*} e^{0.03} &\approx 1.03045 \\ e^{0.16} &\approx 1.17351 \\ e^{0.45} &\approx 1.56831 \\ e^{-0.13} &\approx 0.87811 \\ e^{0.27} &\approx 1.31002 \\ e^{-0.01} &\approx 0.99005 \\ e^{0.32} &\approx 1.37713 \end{align*}\]Soma das exponenciais:
\[\sum_{j=0}^{6} e^{z_j} \approx 7.32758\]Probabilidades após softmax:
\[\begin{align*} P(\text{o} \vert \text{preto}) &= \frac{e^{0.03}}{\sum e^{z_j}} \approx \frac{1.03045}{7.32758} \approx 0.14064 \\ P(\text{gato} \vert \text{preto}) &= \frac{e^{0.16}}{\sum e^{z_j}} \approx \frac{1.17351}{7.32758} \approx 0.16016 \\ P(\text{preto} \vert \text{preto}) &= \frac{e^{0.45}}{\sum e^{z_j}} \approx \frac{1.56831}{7.32758} \approx 0.21402 \\ P(\text{corre} \vert \text{preto}) &= \frac{e^{-0.13}}{\sum e^{z_j}} \approx \frac{0.87811}{7.32758} \approx 0.11984 \\ P(\text{pelo} \vert \text{preto}) &= \frac{e^{0.27}}{\sum e^{z_j}} \approx \frac{1.31002}{7.32758} \approx 0.17878 \\ P(\text{jardim} \vert \text{preto}) &= \frac{e^{-0.01}}{\sum e^{z_j}} \approx \frac{0.99005}{7.32758} \approx 0.13511 \\ P(\text{cachorro} \vert \text{preto}) &= \frac{e^{0.32}}{\sum e^{z_j}} \approx \frac{1.37713}{7.32758} \approx 0.18795 \end{align*}\] -
Calcular a perda (erro): No SkipGram, calculamos a perda para cada palavra de contexto separadamente. Para as palavras de contexto
\[L_{\text{gato}} = -\log(P(\text{gato} \vert \text{preto})) \approx -\log(0.16016)\] \[L_{\text{gato}} \approx -(-1.832) \approx 1.832\] \[L_{\text{corre}} = -\log(P(\text{corre} \vert \text{preto})) \approx -\log(0.11984)\] \[L_{\text{corre}} \approx -(-2.122) \approx 2.122\]gatoecorre:A perda total para este exemplo será dado por:
\[L = L_{\text{gato}} + L_{\text{corre}} \approx 1.832 + 2.122 = 3.954\] -
Propagação do erro (Backpropagation): Para cada palavra de contexto, calculamos os gradientes $\frac{\partial L_{\text{contexto}}}{\partial z_j}$:
Para o contexto
\[\frac{\partial L_{\text{gato}}}{\partial z_1} = P(\text{gato} \vert \text{preto}) - 1 \approx 0.16016 - 1 = -0.83984\]gato:Para as outras palavras $j \neq 1$:
\[\frac{\partial L_{\text{gato}}}{\partial z_j} = P(w_j \vert \text{preto})\]Similarmente para o contexto
\[\frac{\partial L_{\text{corre}}}{\partial z_3} = P(\text{corre} \vert \text{preto}) - 1 \approx 0.11984 - 1 = -0.88016\]corre:Para as outras palavras $j \neq 3$:
\[\frac{\partial L_{\text{corre}}}{\partial z_j} = P(w_j \vert \text{preto})\]Atualização dos pesos da matriz de saída: Para cada palavra de contexto (
gatoecorre), atualizamos as colunas correspondentes na matriz $W_{\text{saída}}$:Para o contexto
\[\Delta W_{\text{saída}, :, 1} = \eta \cdot \frac{\partial L_{\text{gato}}}{\partial z_1} \cdot v_{\text{preto}}^T\]gato(coluna 1):Assumindo $\eta = 0.01$:
\[\Delta W_{\text{saída}, 1}^T = 0.01 \cdot (-0.83984) \cdot [0.4, -0.3, 0.1, 0.5]\] \[\Delta W_{\text{saída}, 1}^T \approx -0.0083984 \cdot [0.4, -0.3, 0.1, 0.5]\] \[\Delta W_{\text{saída}, 1}^T \approx [-0.003359, 0.002520, -0.000840, -0.004199]\]De maneira similar para o contexto
corre(coluna 3).Gradiente para o vetor de embedding da palavra-alvo: Calculamos o gradiente para o vetor de embedding de
preto:Para o contexto
\[\frac{\partial L_{\text{gato}}}{\partial v_{\text{preto}}} = \sum_{j=0}^{6} \frac{\partial L_{\text{gato}}}{\partial z_j} \cdot (\text{linha } j \text{ de } W_{\text{saída}}^T)\]gato:De forma análoga para o contexto
\[\frac{\partial L_{\text{corre}}}{\partial v_{\text{preto}}} = \sum_{j=0}^{6} \frac{\partial L_{\text{corre}}}{\partial z_j} \cdot (\text{linha } j \text{ de } W_{\text{saída}}^T)\]corre:O gradiente total para $v_{\text{preto}}$ será dado por:
\[\frac{\partial L}{\partial v_{\text{preto}}} = \frac{\partial L_{\text{gato}}}{\partial v_{\text{preto}}} + \frac{\partial L_{\text{corre}}}{\partial v_{\text{preto}}}\]Atualização final: Atualizamos o vetor de embedding da palavra-alvo e os pesos relevantes da matriz de saída:
\[v_{\text{preto}}^{\text{new}} = v_{\text{preto}} - \eta \cdot \frac{\partial L}{\partial v_{\text{preto}}}\] \[W_{\text{saída}, :, 1}^{\text{new}} = W_{\text{saída}, :, 1} - \eta \cdot \frac{\partial L_{\text{gato}}}{\partial z_1} \cdot v_{\text{preto}}^T\] \[W_{\text{saída}, :, 3}^{\text{new}} = W_{\text{saída}, :, 3} - \eta \cdot \frac{\partial L_{\text{corre}}}{\partial z_3} \cdot v_{\text{preto}}^T\]
Este processo deve ser repetido para cada par alvo-contexto em todo o corpus, através de múltiplas épocas de treinamento, ajustando gradualmente os vetores de embedding e os pesos da matriz de saída para melhor capturar as relações contextuais entre as palavras.
Implementação do SkipGram em C++ 20 usando Softmax Completo
No código a seguir a atenta leitora poderá ver uma implementação em C++20 do modelo SkipGram com Softmax Completo. A implementação é feita na unha sem preocupação com performance e , sem bibliotecas externas, para ilustrar o funcionamento interno do algoritmo.
#include <iostream> ///< Para entrada e saída padrão (std::cout).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de sequências.
#include <string> ///< Para std::string, usado em palavras e mensagens.
#include <unordered_map> ///< Para std::unordered_map, usado no mapeamento de palavras.
#include <random> ///< Para geração de números aleatórios (std::mt19937).
#include <cmath> ///< Para funções matemáticas como std::exp, std::sqrt e std::log.
#include <fstream> ///< Para leitura/escrita de arquivos.
#include <algorithm> ///< Para std::sort e outras funções de manipulação.
#include <numeric> ///< Para std::accumulate.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <limits> ///< Para std::numeric_limits.
#include <chrono> ///< Para medir o tempo de execução (std::chrono::high_resolution_clock).
#define NOMINMAX ///< Impede a definição de macros min e max do windows.h que conflitam com a STL
#include <windows.h> ///< Para SetConsoleOutputCP e CP_UTF8 (específico do Windows)
// --- Constantes ---
/** @brief Valor máximo para a entrada da função exponencial para evitar overflow na Softmax. */
const float MAX_EXP_SOFTMAX = 6.0f; // Ajustável conforme necessário
/**
* @struct Word
* @brief Estrutura para representar uma palavra, sua contagem e seu vetor de embedding de ENTRADA.
*/
struct Word {
std::string word; ///< A palavra em si.
std::vector<float> vector; ///< O vetor de embedding de ENTRADA da palavra (v_w).
long long count = 0; ///< Contagem de ocorrências no corpus, inicializada como 0.
};
/**
* @class Word2Vec_SkipGram_Softmax
* @brief Implementação do modelo Word2Vec com SkipGram e Softmax completo.
*
* Esta classe constrói embeddings de palavras a partir de um corpus de texto, utilizando
* a abordagem SkipGram para prever palavras de contexto a partir de uma palavra-alvo.
* Utiliza a função Softmax completa para o cálculo de probabilidades, aderindo ao
* exemplo teórico detalhado no artigo. Suporta treinamento, salvamento/carregamento
* de embeddings, busca de palavras similares e operações de analogia vetorial.
* @note Esta implementação usa Softmax completo e pode ser computacionalmente intensiva
* para vocabulários grandes. Otimizações como Negative Sampling ou Hierarchical Softmax
* são geralmente preferidas na prática.
*/
class Word2Vec_SkipGram_Softmax {
private:
// --- Parâmetros do Modelo ---
int vector_size; ///< Dimensão dos vetores de embedding (d).
int window_size; ///< Tamanho máximo da janela de contexto (c).
float learning_rate; ///< Taxa de aprendizado inicial (eta).
float min_learning_rate; ///< Taxa de aprendizado mínima durante o decaimento.
// --- Vocabulário e Embeddings ---
std::unordered_map<std::string, int> word_to_index; ///< Mapeamento palavra -> índice.
std::vector<Word> vocabulary; ///< Lista de palavras e seus embeddings DE ENTRADA (matriz W_entrada, v_w).
std::vector<std::vector<float>> output_weights; ///< Matriz de pesos de SAÍDA (W_saida, v'_w).
// --- Contagens e Aleatoriedade ---
long long total_words; ///< Total de palavras no corpus.
long long words_processed; ///< Palavras processadas durante o treinamento para decaimento de LR.
mutable std::mt19937 rng; ///< Gerador Mersenne Twister (mutável para operações const).
std::uniform_int_distribution<int> uniform_window; ///< Distribuição para tamanho dinâmico da janela.
/**
* @brief Inicializa os embeddings de entrada (vocabulary[i].vector) e os pesos de saída (output_weights) com valores aleatórios.
*
* Os vetores são inicializados com valores pequenos aleatórios seguindo uma distribuição uniforme,
* conforme prática comum para facilitar a convergência durante o treinamento.
*/
void initializeEmbeddings() {
std::uniform_real_distribution<float> dist(-0.5f / vector_size, 0.5f / vector_size);
output_weights.resize(vocabulary.size(), std::vector<float>(vector_size));
for (size_t i = 0; i < vocabulary.size(); ++i) {
vocabulary[i].vector.resize(vector_size);
for (int j = 0; j < vector_size; ++j) {
vocabulary[i].vector[j] = dist(rng); // Inicializa embedding de entrada v_w
output_weights[i][j] = dist(rng); // Inicializa pesos de saída v'_w (alternativamente, poderiam ser zeros)
}
}
std::cout << "Embeddings de entrada e pesos de saída inicializados para " << vocabulary.size() << " palavras.\n";
}
/**
* @brief Calcula a função Softmax para um vetor de scores, de forma numericamente estável.
* @param scores Vetor de scores (z) para cada palavra no vocabulário.
* @return Vetor de probabilidades (P) após aplicar Softmax.
*/
std::vector<float> softmax(const std::vector<float>& scores) const {
std::vector<float> probabilities(scores.size());
// Encontrar o score máximo para estabilidade numérica (subtrair previne exp(grande_numero))
float max_score = -std::numeric_limits<float>::infinity();
for (float score : scores) {
if (score > max_score) {
max_score = score;
}
}
// Calcular exponenciais e a soma
float sum_exp = 0.0f;
for (size_t i = 0; i < scores.size(); ++i) {
// Limitar a entrada da exponencial também pode ajudar
float val = std::min(scores[i] - max_score, MAX_EXP_SOFTMAX);
float exp_val = std::exp(val);
probabilities[i] = exp_val;
sum_exp += exp_val;
}
// Normalizar para obter probabilidades
if (sum_exp > std::numeric_limits<float>::epsilon()) { // Evita divisão por zero ou número muito pequeno
for (size_t i = 0; i < probabilities.size(); ++i) {
probabilities[i] /= sum_exp;
}
}
else {
// Caso raro onde a soma é zero (todos os scores muito negativos)
// Atribui probabilidade uniforme ou lida de outra forma
for (size_t i = 0; i < probabilities.size(); ++i) {
probabilities[i] = 1.0f / probabilities.size();
}
}
return probabilities;
}
/**
* @brief Treina o modelo para um único par (alvo -> contexto) usando SkipGram e Softmax completo.
*
* Implementa os passos descritos no exemplo SkipGram do artigo:
* 1. Obtém o vetor de embedding da palavra-alvo (v_target).
* 2. Calcula os scores (z) para todas as palavras do vocabulário usando v_target e W_saida.
* 3. Aplica Softmax para obter probabilidades (P) de prever cada palavra como contexto.
* 4. Calcula o erro (gradiente) para a camada de saída (e = P - y_context).
* 5. Propaga o erro para calcular o gradiente do embedding da palavra-alvo (dL/dv_target).
* 6. Atualiza os pesos de saída (W_saida) para todas as palavras do vocabulário.
* 7. Atualiza o embedding de entrada da palavra-alvo (v_target).
*
* @param target_idx Índice da palavra-alvo (entrada).
* @param context_idx Índice da palavra de contexto real a ser prevista (saída).
* @param current_learning_rate Taxa de aprendizado atual para esta atualização.
*/
void trainSkipGramPair(int target_idx, int context_idx, float current_learning_rate) {
// --- Passo 1: Obter vetor de embedding da palavra-alvo ---
const auto& v_target = vocabulary[target_idx].vector;
// --- Passo 3: Calcular scores (z = v_target * W_saida) ---
// z_j = v_target . v'_j (produto escalar de v_target com o vetor de SAÍDA da palavra j)
std::vector<float> scores(vocabulary.size());
for (size_t j = 0; j < vocabulary.size(); ++j) {
float dot_product = 0.0f;
for (int i = 0; i < vector_size; ++i) {
// Usar output_weights[j] que corresponde a v'_j
dot_product += v_target[i] * output_weights[j][i];
}
scores[j] = dot_product;
}
// --- Passo 4: Aplicar Softmax para obter probabilidades (P) ---
std::vector<float> probabilities = softmax(scores);
// --- Passo 6 (Backpropagation): Calcular erro na camada de saída ---
// e = P - y_context, onde y_context é One-Hot para context_idx
std::vector<float> error_output_layer = probabilities; // Copia P
error_output_layer[context_idx] -= 1.0f; // Subtrai 1 na posição do contexto real
// --- Passo 6 (Backpropagation): Calcular gradiente para o embedding da palavra-alvo ---
// dL/dv_target = sum_j (e_j * v'_j) = e * W_saida^T
std::vector<float> gradient_target_embedding(vector_size, 0.0f);
for (int i = 0; i < vector_size; ++i) { // Para cada dimensão do embedding alvo
float sum = 0.0f;
for (size_t j = 0; j < vocabulary.size(); ++j) { // Somar sobre todas as palavras do vocabulário
sum += error_output_layer[j] * output_weights[j][i]; // e_j * v'_j[i]
}
gradient_target_embedding[i] = sum;
}
// --- Passo 6 (Backpropagation): Atualizar Pesos de SAÍDA (W_saida ou v') ---
// dL/dv'_j = dL/dz_j * dz_j/dv'_j = e_j * v_target
// v'_j(novo) = v'_j(antigo) - eta * e_j * v_target
// ATENÇÃO: Isso atualiza TODOS os vetores de saída (v'_j para todo j)
for (size_t j = 0; j < vocabulary.size(); ++j) {
float error_j = error_output_layer[j]; // e_j
for (int i = 0; i < vector_size; ++i) {
output_weights[j][i] -= current_learning_rate * error_j * v_target[i];
}
}
// --- Passo 6 (Backpropagation): Atualizar Embedding de ENTRADA da palavra-alvo (v_target) ---
// v_target(novo) = v_target(antigo) - eta * dL/dv_target
for (int i = 0; i < vector_size; ++i) {
// Acessar e modificar diretamente o vetor na estrutura Word
vocabulary[target_idx].vector[i] -= current_learning_rate * gradient_target_embedding[i];
}
}
public:
/**
* @brief Construtor que inicializa os parâmetros do modelo SkipGram com Softmax.
* @param vector_size Dimensão dos vetores de embedding (padrão: 100).
* @param window_size Tamanho máximo da janela de contexto (padrão: 5).
* @param learning_rate Taxa de aprendizado inicial (padrão: 0.025, comum para SkipGram).
*/
Word2Vec_SkipGram_Softmax(int vector_size = 100, int window_size = 5, float learning_rate = 0.025f)
: vector_size(vector_size), window_size(window_size),
learning_rate(learning_rate), min_learning_rate(learning_rate * 0.0001f),
total_words(0), words_processed(0), rng(std::random_device{}()) {
uniform_window = std::uniform_int_distribution<int>(1, window_size); // Janela dinâmica [1, window_size]
std::cout << "Modelo Word2Vec SkipGram (Softmax Completo) inicializado.\n";
std::cout << " Dimensão Vetores (d): " << vector_size << "\n";
std::cout << " Tamanho Janela (c): " << window_size << "\n";
std::cout << " Taxa Aprendizado (eta): " << learning_rate << "\n";
std::cout << " Aviso: Usando Softmax completo. Treinamento pode ser lento para vocabulários grandes.\n";
}
/**
* @brief Constrói o vocabulário a partir de um corpus de texto.
*
* Conta as ocorrências de cada palavra e mapeia palavras para índices.
* Após construir o vocabulário, inicializa os embeddings de entrada e saída.
*
* @param corpus Vetor de sentenças, onde cada sentença é um vetor de palavras (strings).
*/
void buildVocabulary(const std::vector<std::vector<std::string>>& corpus) {
std::cout << "Construindo vocabulário...\n";
std::unordered_map<std::string, long long> word_counts;
total_words = 0;
// Contar ocorrências
for (const auto& sentence : corpus) {
for (const auto& word : sentence) {
word_counts[word]++;
total_words++;
}
}
// Verificar se o corpus é válido
if (word_counts.empty()) {
std::cerr << "Erro: Corpus vazio ou inválido. Vocabulário não pode ser construído.\n";
return;
}
std::cout << " Total de palavras no corpus: " << total_words << "\n";
std::cout << " Número de palavras únicas: " << word_counts.size() << "\n";
// Construir vocabulário
vocabulary.clear();
word_to_index.clear();
int index = 0;
// Poderíamos adicionar filtragem por frequência mínima aqui se necessário
for (const auto& [word, count] : word_counts) {
Word w;
w.word = word;
w.count = count;
// Não redimensionar o vetor aqui, será feito em initializeEmbeddings
vocabulary.push_back(w);
word_to_index[word] = index++;
}
// Inicializar embeddings de entrada e pesos de saída
initializeEmbeddings();
std::cout << "Vocabulário construído e embeddings inicializados.\n";
}
/**
* @brief Treina o modelo SkipGram com Softmax completo.
*
* Itera sobre o corpus por um número definido de épocas. Em cada época,
* para cada palavra-alvo, itera sobre suas palavras de contexto e chama
* `trainSkipGramPair` para ajustar os embeddings e pesos usando Softmax.
* A taxa de aprendizado diminui linearmente ao longo das épocas com base
* no número total de palavras-alvo processadas.
*
* @param corpus Vetor de sentenças para treinamento.
* @param epochs Número de épocas de treinamento (padrão: 15).
*/
void trainSkipGram(const std::vector<std::vector<std::string>>& corpus, int epochs = 15) {
if (vocabulary.empty()) {
std::cerr << "Erro: Vocabulário não inicializado. Execute buildVocabulary primeiro.\n";
return;
}
std::cout << "Iniciando treinamento SkipGram (Softmax) por " << epochs << " épocas...\n";
float initial_lr = learning_rate;
words_processed = 0; // Reiniciar contagem de palavras processadas
// Estimativa para decaimento de LR (total de palavras-alvo a serem processadas)
long long total_training_words_estimate = static_cast<long long>(total_words) * epochs;
for (int epoch = 0; epoch < epochs; ++epoch) {
long long epoch_words_processed = 0; // Palavras-alvo processadas nesta época
long long pairs_trained = 0; // Pares (alvo, contexto) treinados nesta época
for (const auto& sentence : corpus) {
for (size_t i = 0; i < sentence.size(); ++i) {
// Encontrar índice da palavra-alvo (entrada)
auto target_it = word_to_index.find(sentence[i]);
if (target_it == word_to_index.end()) continue; // Palavra fora do vocabulário
int target_idx = target_it->second;
// --- CORREÇÃO: Calcular current_lr AQUI ---
// Calcula a taxa de aprendizado atual ANTES do loop de contexto
// baseado no progresso GERAL do treinamento (total de palavras-alvo processadas)
float progress = 0.0f;
if (total_training_words_estimate > 0) {
progress = static_cast<float>(words_processed) / total_training_words_estimate;
}
float current_lr = initial_lr * (1.0f - progress);
current_lr = std::max(current_lr, min_learning_rate); // Garante LR mínimo
// --- FIM CORREÇÃO ---
// Determinar janela de contexto dinâmica
int current_window = uniform_window(rng);
// Iterar sobre as posições de contexto
for (int j = -current_window; j <= current_window; ++j) {
if (j == 0) continue; // Pular a palavra-alvo
size_t context_pos = i + j;
// Verificar limites da sentença
if (context_pos < sentence.size()) { // size_t é sempre >= 0
auto context_it = word_to_index.find(sentence[context_pos]);
if (context_it != word_to_index.end()) {
int context_idx = context_it->second; // Palavra de contexto real (saída)
// Treinar o par (alvo -> contexto) - Passa a LR já calculada
trainSkipGramPair(target_idx, context_idx, current_lr);
pairs_trained++;
}
}
} // Fim do loop de contexto
epoch_words_processed++; // Incrementa contador da época
words_processed++; // Incrementa contador GERAL
// Exibir progresso (opcional, pode desacelerar)
// Usa 'current_lr' que agora está no escopo correto
if (epoch_words_processed % 10000 == 0) {
std::cout << "\rÉpoca " << epoch + 1 << "/" << epochs
<< ", Progresso Estimado: " << std::fixed << std::setprecision(2)
<< 100.0f * progress << "%, LR: " << current_lr // AGORA VÁLIDO
<< std::flush;
}
} // Fim do loop da sentença
} // Fim do loop do corpus
// Imprime resumo da época - Recalcula a LR final aproximada da época para exibição
float final_epoch_progress = 0.0f;
if (total_training_words_estimate > 0) {
final_epoch_progress = static_cast<float>(words_processed) / total_training_words_estimate;
}
float final_epoch_lr = std::max(initial_lr * (1.0f - final_epoch_progress), min_learning_rate);
std::cout << "\n Época " << epoch + 1 << "/" << epochs << " completa. Pares treinados: " << pairs_trained
<< ". LR final aprox: " << std::fixed << std::setprecision(6) << final_epoch_lr << "\n";
} // Fim do loop das épocas
std::cout << "Treinamento SkipGram (Softmax) concluído.\n";
}
/**
* @brief Salva os embeddings de ENTRADA em um arquivo no formato texto Word2Vec.
* @param filename Nome do arquivo de saída.
* @note Salva apenas os vetores de entrada (v_w), que são tipicamente usados como embeddings.
*/
void saveEmbeddings(const std::string& filename) const {
std::cout << "Salvando embeddings de entrada em " << filename << "...\n";
std::ofstream file(filename);
if (!file.is_open()) {
std::cerr << "Erro ao abrir arquivo para escrita: " << filename << "\n";
return;
}
// Cabeçalho: número_de_palavras dimensão_vetor
file << vocabulary.size() << " " << vector_size << "\n";
// Linhas: palavra val1 val2 ... valN
for (const auto& word : vocabulary) {
file << word.word;
for (float val : word.vector) {
file << " " << std::fixed << std::setprecision(6) << val;
}
file << "\n";
}
file.close();
std::cout << "Embeddings salvos com sucesso.\n";
}
/**
* @brief Carrega embeddings pré-treinados de um arquivo (APENAS vetores de entrada).
* @param filename Nome do arquivo de entrada.
* @return True se o carregamento for bem-sucedido, false caso contrário.
* @note Assume formato texto Word2Vec. Carrega apenas os vetores de entrada (v_w).
* Os pesos de saída (v'_w) precisarão ser inicializados se for continuar o treinamento.
*/
bool loadEmbeddings(const std::string& filename) {
std::cout << "Carregando embeddings de ENTRADA de " << filename << "...\n";
std::ifstream file(filename);
if (!file.is_open()) {
std::cerr << "Erro ao abrir arquivo para leitura: " << filename << "\n";
return false;
}
size_t vocab_size;
int loaded_vector_size;
file >> vocab_size >> loaded_vector_size;
// Verifica se a dimensão do vetor carregado corresponde à configuração do modelo
if (file.fail() || loaded_vector_size <= 0) {
std::cerr << "Erro ao ler cabeçalho do arquivo: " << filename << "\n";
return false;
}
std::cout << " Arquivo contém " << vocab_size << " palavras com dimensão " << loaded_vector_size << ".\n";
// Permite carregar embeddings com dimensão diferente, ajustando o modelo
if (loaded_vector_size != vector_size) {
std::cout << " Aviso: Dimensão do vetor no arquivo (" << loaded_vector_size
<< ") difere da configuração do modelo (" << vector_size
<< "). Ajustando modelo para " << loaded_vector_size << ".\n";
vector_size = loaded_vector_size;
}
vocabulary.clear();
word_to_index.clear();
vocabulary.reserve(vocab_size);
for (size_t i = 0; i < vocab_size; ++i) {
Word w;
file >> w.word;
if (file.fail()) {
std::cerr << "Erro ao ler palavra no índice " << i << " do arquivo.\n";
return false;
}
w.vector.resize(vector_size); // Redimensiona o vetor de entrada
for (int j = 0; j < vector_size; ++j) {
file >> w.vector[j];
if (file.fail()) {
std::cerr << "Erro ao ler valor do vetor para a palavra '" << w.word << "' no índice " << j << ".\n";
return false;
}
}
w.count = 1; // Contagem desconhecida ao carregar
vocabulary.push_back(w);
word_to_index[w.word] = i;
}
file.close();
// IMPORTANTE: Os pesos de SAÍDA NÃO são carregados por este método.
// Se for continuar o treinamento, eles precisam ser (re)inicializados.
// Vamos inicializá-los aleatoriamente aqui para permitir treinamento adicional.
output_weights.resize(vocabulary.size(), std::vector<float>(vector_size));
std::uniform_real_distribution<float> dist(-0.5f / vector_size, 0.5f / vector_size);
for (size_t i = 0; i < vocabulary.size(); ++i) {
for (int j = 0; j < vector_size; ++j) {
output_weights[i][j] = dist(rng);
}
}
total_words = vocabulary.size(); // Estimativa grosseira se não tivermos o corpus original
std::cout << "Embeddings de ENTRADA carregados e pesos de SAÍDA (re)inicializados com sucesso.\n";
return true;
}
/**
* @brief Encontra as palavras com maior grau de similaridade a uma palavra dada usando similaridade de cosseno nos embeddings de ENTRADA.
* @param word Palavra de consulta.
* @param top_n Número de palavras similares a retornar (padrão: 10).
* @return Vetor de pares (palavra, similaridade), ordenado por similaridade decrescente.
*/
std::vector<std::pair<std::string, float>> findSimilar(const std::string& word, int top_n = 10) const {
auto it = word_to_index.find(word);
if (it == word_to_index.end()) {
std::cerr << "Aviso: Palavra '" << word << "' não encontrada no vocabulário para busca de similaridade.\n";
return {};
}
int word_idx = it->second;
const auto& word_vector = vocabulary[word_idx].vector; // Usa vetor de ENTRADA (v_w)
std::vector<std::pair<std::string, float>> similarities;
similarities.reserve(vocabulary.size());
for (size_t i = 0; i < vocabulary.size(); ++i) {
if (i == word_idx) continue; // Não comparar a palavra consigo mesma
// Compara vetores de ENTRADA (v_w com outros v_w)
float similarity = cosineSimilarity(word_vector, vocabulary[i].vector);
similarities.emplace_back(vocabulary[i].word, similarity);
}
// Ordenar por similaridade decrescente
std::sort(similarities.begin(), similarities.end(),
[](const auto& a, const auto& b) { return a.second > b.second; });
// Retornar os top_n resultados
if (similarities.size() > static_cast<size_t>(top_n)) {
similarities.resize(top_n);
}
return similarities;
}
/**
* @brief Calcula a similaridade de cosseno entre dois vetores.
* @param a Primeiro vetor.
* @param b Segundo vetor.
* @return Valor da similaridade de cosseno [-1, 1]. Retorna 0 se uma das normas for zero.
*/
float cosineSimilarity(const std::vector<float>& a, const std::vector<float>& b) const {
if (a.size() != b.size() || a.empty()) {
return 0.0f; // Vetores incompatíveis ou vazios
}
float dot_product = 0.0f;
float norm_a = 0.0f;
float norm_b = 0.0f;
for (size_t i = 0; i < a.size(); ++i) {
dot_product += a[i] * b[i];
norm_a += a[i] * a[i];
norm_b += b[i] * b[i];
}
// Evitar divisão por zero se um vetor for nulo (norma zero)
norm_a = std::sqrt(norm_a);
norm_b = std::sqrt(norm_b);
if (norm_a < std::numeric_limits<float>::epsilon() || norm_b < std::numeric_limits<float>::epsilon()) {
return 0.0f;
}
return dot_product / (norm_a * norm_b);
}
/**
* @brief Realiza operações de analogia vetorial (a - b + c ≈ ?) usando os embeddings de ENTRADA.
*
* Calcula o vetor resultante `vec(a) - vec(b) + vec(c)` e encontra as palavras
* cujos vetores de embedding de entrada (v_w) são mais próximos a ele via similaridade de cosseno.
*
* @param a Primeira palavra positiva.
* @param b Palavra negativa.
* @param c Segunda palavra positiva.
* @param top_n Número de resultados a retornar (padrão: 5).
* @return Vetor de pares (palavra, similaridade).
*/
std::vector<std::pair<std::string, float>> analogy(const std::string& a,
const std::string& b,
const std::string& c,
int top_n = 5) const {
auto it_a = word_to_index.find(a);
auto it_b = word_to_index.find(b);
auto it_c = word_to_index.find(c);
if (it_a == word_to_index.end() || it_b == word_to_index.end() || it_c == word_to_index.end()) {
std::cerr << "Aviso: Uma ou mais palavras da analogia (" << a << ", " << b << ", " << c << ") não encontradas no vocabulário.\n";
return {};
}
const auto& vec_a = vocabulary[it_a->second].vector; // Vetor de ENTRADA (v_w)
const auto& vec_b = vocabulary[it_b->second].vector; // Vetor de ENTRADA (v_w)
const auto& vec_c = vocabulary[it_c->second].vector; // Vetor de ENTRADA (v_w)
std::vector<float> result_vec(vector_size);
for (int i = 0; i < vector_size; ++i) {
result_vec[i] = vec_a[i] - vec_b[i] + vec_c[i];
}
// Normalizar o vetor resultante (opcional, mas melhora a comparação por cosseno)
float norm = 0.0f;
for (float val : result_vec) {
norm += val * val;
}
norm = std::sqrt(norm);
if (norm > std::numeric_limits<float>::epsilon()) {
for (float& val : result_vec) {
val /= norm;
}
}
// Encontrar palavras com maior grau de similaridade ao vetor resultante (usando vetores de ENTRADA)
std::vector<std::pair<std::string, float>> similarities;
similarities.reserve(vocabulary.size());
for (size_t i = 0; i < vocabulary.size(); ++i) {
// Não incluir as palavras de entrada na lista de resultados
if (i == it_a->second || i == it_b->second || i == it_c->second) {
continue;
}
// Compara o vetor resultante com os vetores de ENTRADA das outras palavras
float similarity = cosineSimilarity(result_vec, vocabulary[i].vector);
similarities.emplace_back(vocabulary[i].word, similarity);
}
// Ordenar e retornar top_n
std::sort(similarities.begin(), similarities.end(),
[](const auto& x, const auto& y) { return x.second > y.second; });
if (similarities.size() > static_cast<size_t>(top_n)) {
similarities.resize(top_n);
}
return similarities;
}
/**
* @brief Retorna o vetor embedding de ENTRADA (v_w) de uma palavra.
* @param word Palavra de consulta.
* @return Vetor de embedding de entrada. Retorna um vetor de zeros se a palavra não for encontrada.
*/
std::vector<float> getWordVector(const std::string& word) const {
auto it = word_to_index.find(word);
if (it == word_to_index.end()) {
std::cerr << "Aviso: Palavra '" << word << "' não encontrada no vocabulário para getWordVector.\n";
return std::vector<float>(vector_size, 0.0f);
}
return vocabulary[it->second].vector; // Retorna vetor de ENTRADA (v_w)
}
};
/**
* @brief Função principal que demonstra o uso da classe Word2Vec_SkipGram_Softmax.
*
* Cria um modelo SkipGram com Softmax completo, constrói o vocabulário, treina,
* e demonstra funcionalidades como busca de similares, analogia e salvamento.
* @note O treinamento pode ser lento devido ao Softmax completo.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
// Configurar o console para UTF-8 (Específico do Windows)
#ifdef _WIN32
SetConsoleOutputCP(CP_UTF8);
std::cout << "Console configurado para UTF-8.\n";
#endif
// Corpus simplificado (o mesmo dos exemplos anteriores)
std::vector<std::vector<std::string>> corpus = {
{"o", "gato", "preto", "corre", "pelo", "jardim"},
{"o", "cachorro", "late", "para", "o", "gato"},
{"gatos", "e", "cachorros", "são", "animais", "domésticos"},
{"muitas", "pessoas", "gostam", "de", "ter", "um", "animal", "de", "estimação"},
{"os", "gatos", "gostam", "de", "dormir", "durante", "o", "dia"},
{"os", "cachorros", "precisam", "passear", "todos", "os", "dias"}
};
std::cout << "Corpus de exemplo carregado com " << corpus.size() << " sentenças.\n";
// --- Criar e Treinar Modelo SkipGram (Softmax) ---
// Usar parâmetros menores e LR possivelmente maior que NegSampling para o exemplo pequeno
// Nota: LR de 0.05f pode ser razoável para este pequeno exemplo com Softmax.
Word2Vec_SkipGram_Softmax model(20, 2, 0.05f); // Dimensão 20, Janela 2, LR 0.05
// Medir Construção do Vocabulário
auto start_vocab = std::chrono::high_resolution_clock::now();
model.buildVocabulary(corpus);
auto end_vocab = std::chrono::high_resolution_clock::now();
auto duration_vocab = std::chrono::duration_cast<std::chrono::milliseconds>(end_vocab - start_vocab);
std::cout << "Tempo de construção do vocabulário: " << duration_vocab.count() << " ms\n";
// Medir Treinamento (Softmax será mais lento)
int epochs_count = 100; // Pode precisar de mais épocas com Softmax em corpus pequeno
auto start_train = std::chrono::high_resolution_clock::now();
model.trainSkipGram(corpus, epochs_count);
auto end_train = std::chrono::high_resolution_clock::now();
auto duration_train = std::chrono::duration_cast<std::chrono::milliseconds>(end_train - start_train);
std::cout << "Tempo de treinamento (" << epochs_count << " épocas): " << duration_train.count() << " ms\n";
// --- Usar o Modelo Treinado ---
// Encontrar palavras similares a 'gato'
std::cout << "\n--- Palavras similares a 'gato' (SkipGram Softmax) ---\n";
auto similar_to_cat = model.findSimilar("gato", 5);
if (similar_to_cat.empty()) {
std::cout << "Nenhuma palavra similar encontrada.\n";
}
else {
for (const auto& [word, similarity] : similar_to_cat) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
}
}
// Encontrar palavras similares a 'cachorro'
std::cout << "\n--- Palavras similares a 'cachorro' (SkipGram Softmax) ---\n";
auto similar_to_dog = model.findSimilar("cachorro", 5);
if (similar_to_dog.empty()) {
std::cout << "Nenhuma palavra similar encontrada.\n";
}
else {
for (const auto& [word, similarity] : similar_to_dog) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
}
}
// Testar analogia: gato - gatos + cachorro ≈ cachorros ?
std::cout << "\n--- Analogia (SkipGram Softmax): gato - gatos + cachorro = ? ---\n";
auto analogy_results = model.analogy("gato", "gatos", "cachorro", 3);
if (analogy_results.empty()) {
std::cout << "Não foi possível calcular a analogia.\n";
}
else {
for (const auto& [word, similarity] : analogy_results) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
}
}
// Obter vetor de uma palavra específica
std::cout << "\n--- Vetor da palavra 'animal' (SkipGram Softmax) ---\n";
std::vector<float> vec_animal = model.getWordVector("animal");
// Verifica se o vetor retornado não é o vetor de zeros (indicando palavra não encontrada)
bool animal_found = false;
for (float val : vec_animal) { if (std::abs(val) > 1e-9) { animal_found = true; break; } }
if (animal_found) {
std::cout << " [";
for (size_t i = 0; i < vec_animal.size(); ++i) {
std::cout << std::fixed << std::setprecision(3) << vec_animal[i] << (i == vec_animal.size() - 1 ? "" : ", ");
}
std::cout << "]\n";
}
else {
std::cout << " Palavra 'animal' não encontrada ou vetor nulo.\n";
}
// Salvar os embeddings de entrada resultantes
model.saveEmbeddings("SkipGram_softmax_word_embeddings.txt");
std::cout << "\nExecução concluída.\n";
return 0;
}
Vantagens e Desvantagens do SkipGram
| Vantagens | Desvantagens |
|---|---|
| Melhor desempenho para palavras raras, pois cada ocorrência gera múltiplos exemplos de treinamento | Computacionalmente mais intensivo, especialmente para palavras frequentes |
| Captura melhor múltiplos sentidos de palavras (polissemia) | Produz mais exemplos de treinamento, tornando o processo mais lento |
| Maior precisão em tarefas de analogia semântica (rei-homem+mulher≈rainha) | Requer mais ajustes de hiperparâmetros para convergência ótima |
| Demonstra melhor generalização em conjuntos de dados pequenos | Maior susceptibilidade a overfitting sem regularização adequada |
Otimizações Críticas para Word2Vec
Na prática, treinar os modelos CBoW e SkipGram como descritos acima seria computacionalmente inviável para corpus grandes. Mikolov et al. introduziram duas otimizações críticas que tornaram esses algoritmos práticos e escaláveis para grandes volumes de dados textuais.
Negative Sampling
O maior gargalo computacional no treinamento do Word2Vec é o cálculo do softmax, que requer uma normalização sobre todo o vocabulário. O Negative Sampling transforma este problema computacionalmente intensivo em uma série de problemas de classificação binária mais simples.
A ideia fundamental é: para cada exemplo positivo (palavra-alvo e palavra de contexto real), amostramos $k$ exemplos negativos (palavras aleatórias que não são o contexto real). O objetivo se torna maximizar a probabilidade da palavra de contexto real enquanto minimizamos a probabilidade das palavras negativas amostradas.
Matematicamente, a função objetivo se torna:
$\log \sigma(v’{w_O}v{w_I}) + \sum_{i=1}^{k} \mathbb{E}{w_i \sim P_n(w)} [\log \sigma(-v’{w_i}v_{w_I})]$
Na qual:
- $\sigma$ é a função sigmoide $\sigma(x) = \frac{1}{1+e^{-x}}$;
- $P_n(w)$ é a distribuição de amostragem, geralmente proporcional a $f(w)^{0.75}$, onde $f(w)$ é a frequência da palavra.
Este método reduz a complexidade computacional de $O(vert V \vert)$ para $O(k)$, onde $k$ é tipicamente entre $5$-$20$, diminuindo muito o tempo de treinamento.
Implementação em C++ do SkipGram com Negative Sampling
A seguir, a curiosa leitora poderá ver uma implementação do modelo SkipGram com Negative Sampling em C++20. Novamente, na unha.
#include <iostream> ///< Para entrada e saída padrão (std::cout).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de sequências.
#include <string> ///< Para std::string, usado em palavras e mensagens.
#include <unordered_map> ///< Para std::unordered_map, usado no mapeamento de palavras.
#include <random> ///< Para geração de números aleatórios (std::mt19937).
#include <cmath> ///< Para funções matemáticas como std::exp e std::sqrt.
#include <fstream> ///< Para leitura/escrita de arquivos.
#include <algorithm> ///< Para std::sort e outras funções de manipulação.
#include <numeric> ///< Para std::accumulate.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <chrono> ///< Para medir o tempo de execução (std::chrono::high_resolution_clock).
#define NOMINMAX ///< Impede a definição de macros min e max que conflitam com a STL
#include <windows.h> ///< Para SetConsoleOutputCP e CP_UTF8 (específico do Windows)
// --- Constantes ---
/** @brief Valor máximo para a entrada da função sigmóide para evitar overflow. */
const float MAX_EXP = 6.0f;
/** @brief Número de intervalos na tabela pré-computada de sigmóide. */
const int EXP_TABLE_SIZE = 1000;
/**
* @struct Word
* @brief Estrutura para representar uma palavra, sua contagem e seu vetor embedding.
*/
struct Word {
std::string word; ///< A palavra em si.
std::vector<float> vector; ///< O vetor de embedding da palavra.
long long count = 0; ///< Contagem de ocorrências no corpus.
};
/**
* @class Word2Vec_SkipGram
* @brief Implementação do modelo Word2Vec com SkipGram e Negative Sampling.
*/
class Word2Vec_SkipGram {
private:
// --- Parâmetros do Modelo ---
int vector_size; ///< Dimensão dos vetores de embedding (d).
int window_size; ///< Tamanho máximo da janela de contexto (c).
int negative_samples; ///< Número de amostras negativas por par positivo (k).
float learning_rate; ///< Taxa de aprendizado inicial (eta).
float min_learning_rate; ///< Taxa de aprendizado mínima.
// --- Vocabulário e Embeddings ---
std::unordered_map<std::string, int> word_to_index; ///< Mapeamento palavra -> índice.
std::vector<Word> vocabulary; ///< Lista de palavras e seus embeddings (v_w).
std::vector<std::vector<float>> output_weights; ///< Matriz de pesos de saída (v'_w).
// --- Tabelas e Contagens ---
std::vector<float> exp_table; ///< Tabela pré-computada para sigmoid(x).
std::vector<int> negative_table; ///< Tabela para amostragem negativa.
static const int negative_table_size = 100000000; ///< Tamanho da tabela de amostragem negativa.
long long total_words; ///< Total de palavras no corpus.
long long words_processed; ///< Palavras processadas durante treinamento.
// --- Geração de Números Aleatórios ---
mutable std::mt19937 rng; ///< Gerador Mersenne Twister.
std::uniform_int_distribution<int> uniform_window; ///< Distribuição para tamanho da janela.
std::uniform_int_distribution<int> uniform_negative; ///< Distribuição para amostragem negativa.
/**
* @brief Inicializa tabela pré-computada para a função sigmóide.
*
* Pré-calcula valores da função sigmoid(x) para melhorar performance durante treinamento.
*/
void initExpTable() {
exp_table.resize(EXP_TABLE_SIZE);
for (int i = 0; i < EXP_TABLE_SIZE; i++) {
// Mapeia índice i para valor x entre -MAX_EXP e MAX_EXP
float x = (2.0f * MAX_EXP * i / EXP_TABLE_SIZE - MAX_EXP);
exp_table[i] = std::exp(x);
}
}
/**
* @brief Inicializa tabela de amostragem negativa baseada na distribuição de frequência.
*
* Cria uma tabela de índices onde palavras mais frequentes aparecem mais vezes,
* permitindo amostragem negativa eficiente proporcional a P(w) ~ f(w)^0.75
*/
void initNegativeTable() {
negative_table.resize(negative_table_size);
const float power = 0.75f;
double total_pow_freq = 0.0;
std::vector<double> powered_freqs(vocabulary.size());
// Calcular f(w)^0.75 para todas as palavras
for (size_t i = 0; i < vocabulary.size(); i++) {
powered_freqs[i] = std::pow(vocabulary[i].count / (double)total_words, power);
total_pow_freq += powered_freqs[i];
}
// Preencher a tabela com índices proporcionais à frequência ajustada
int table_idx = 0;
for (size_t word_idx = 0; word_idx < vocabulary.size(); word_idx++) {
// Número de entradas na tabela para esta palavra
int entries = static_cast<int>(powered_freqs[word_idx] / total_pow_freq * negative_table_size);
for (int j = 0; j < entries && table_idx < negative_table_size; j++) {
negative_table[table_idx++] = word_idx;
}
}
// Preencher o restante da tabela se necessário
while (table_idx < negative_table_size) {
negative_table[table_idx++] = 0; // Usar a primeira palavra como fallback
}
std::cout << "Tabela de amostragem negativa inicializada.\n";
}
/**
* @brief Inicializa os vetores de embedding com pequenos valores aleatórios.
*/
void initializeEmbeddings() {
std::uniform_real_distribution<float> dist(-0.5f / vector_size, 0.5f / vector_size);
output_weights.resize(vocabulary.size(), std::vector<float>(vector_size));
for (size_t i = 0; i < vocabulary.size(); ++i) {
vocabulary[i].vector.resize(vector_size);
for (int j = 0; j < vector_size; ++j) {
vocabulary[i].vector[j] = dist(rng); // Inicializa embedding de entrada (v_w)
output_weights[i][j] = 0.0f; // Inicializa pesos de saída (v'_w) com zeros
}
}
std::cout << "Embeddings inicializados para " << vocabulary.size() << " palavras.\n";
}
/**
* @brief Obtém valor da função sigmóide usando a tabela pré-computada.
* @param x Valor de entrada.
* @return Valor sigmóide aproximado (1/(1+exp(-x))).
*/
float sigmoid(float x) const {
if (x > MAX_EXP) return 1.0f;
else if (x < -MAX_EXP) return 0.0f;
// Mapeia x do intervalo [-MAX_EXP, MAX_EXP] para [0, EXP_TABLE_SIZE-1]
int idx = (int)((x + MAX_EXP) * (EXP_TABLE_SIZE / (2 * MAX_EXP)));
if (idx >= EXP_TABLE_SIZE) idx = EXP_TABLE_SIZE - 1;
if (idx < 0) idx = 0;
return 1.0f / (1.0f + exp_table[idx]);
}
/**
* @brief Amostra uma palavra negativa para treinamento.
* @param target_idx Índice da palavra alvo a evitar.
* @param context_idx Índice da palavra de contexto a evitar.
* @return Índice de uma palavra amostrada aleatoriamente.
*/
int sampleNegative(int target_idx, int context_idx) const {
int sampled_idx;
do {
sampled_idx = negative_table[uniform_negative(rng)];
} while (sampled_idx == target_idx || sampled_idx == context_idx);
return sampled_idx;
}
/**
* @brief Treina o modelo com um par alvo-contexto e atualizações de Negative Sampling.
*
* Implementa o treinamento de um único par positivo (palavra-alvo, palavra-contexto)
* junto com k pares negativos. Atualiza os vetores de embedding usando gradiente descendente.
*
* @param target_idx Índice da palavra alvo (w_I).
* @param context_idx Índice da palavra de contexto (w_O).
* @param alpha Taxa de aprendizado atual.
*/
void trainPair(int target_idx, int context_idx, float alpha) {
// Vetores temporários para acumular gradientes
std::vector<float> neu1e(vector_size, 0.0f);
// 1. Treinar par positivo (target prediz context)
float dot_product = 0.0f;
for (int i = 0; i < vector_size; ++i) {
dot_product += vocabulary[target_idx].vector[i] * output_weights[context_idx][i];
}
// Limitar dot_product para evitar overflow
if (dot_product > MAX_EXP) dot_product = MAX_EXP;
else if (dot_product < -MAX_EXP) dot_product = -MAX_EXP;
// Calcular erro para o par positivo
float g = (1.0f - sigmoid(dot_product)) * alpha;
// Acumular erro para atualizar embedding da palavra alvo
for (int i = 0; i < vector_size; ++i) {
neu1e[i] += g * output_weights[context_idx][i];
output_weights[context_idx][i] += g * vocabulary[target_idx].vector[i];
}
// 2. Treinar pares negativos (target NÃO prediz palavras negativas)
for (int neg = 0; neg < negative_samples; ++neg) {
int negative_idx = sampleNegative(target_idx, context_idx);
dot_product = 0.0f;
for (int i = 0; i < vector_size; ++i) {
dot_product += vocabulary[target_idx].vector[i] * output_weights[negative_idx][i];
}
// Limitar dot_product
if (dot_product > MAX_EXP) dot_product = MAX_EXP;
else if (dot_product < -MAX_EXP) dot_product = -MAX_EXP;
// O objetivo é que target NÃO prediga a palavra negativa, então o alvo é 0 aqui
float g_neg = sigmoid(dot_product) * alpha;
// Acumular erro para atualizar embedding da palavra alvo
for (int i = 0; i < vector_size; ++i) {
neu1e[i] += g_neg * output_weights[negative_idx][i];
output_weights[negative_idx][i] += g_neg * vocabulary[target_idx].vector[i];
}
}
// 3. Atualizar embedding da palavra alvo com gradiente acumulado
for (int i = 0; i < vector_size; ++i) {
vocabulary[target_idx].vector[i] += neu1e[i];
}
}
public:
/**
* @brief Construtor que inicializa os parâmetros do modelo SkipGram.
* @param vector_size Dimensão dos vetores de embedding (padrão: 100).
* @param window_size Tamanho máximo da janela de contexto (padrão: 5).
* @param negative_samples Número de amostras negativas por par (padrão: 5).
* @param learning_rate Taxa de aprendizado inicial (padrão: 0.025).
*/
Word2Vec_SkipGram(int vector_size = 100, int window_size = 5,
int negative_samples = 5, float learning_rate = 0.025f)
: vector_size(vector_size), window_size(window_size),
negative_samples(negative_samples), learning_rate(learning_rate),
min_learning_rate(learning_rate * 0.0001f),
total_words(0), words_processed(0),
rng(std::random_device{}()) {
uniform_window = std::uniform_int_distribution<int>(1, window_size);
uniform_negative = std::uniform_int_distribution<int>(0, negative_table_size - 1);
initExpTable();
std::cout << "Modelo Word2Vec SkipGram inicializado.\n";
std::cout << " Dimensão Vetores (d): " << vector_size << "\n";
std::cout << " Tamanho Janela (c): " << window_size << "\n";
std::cout << " Amostras Negativas (k): " << negative_samples << "\n";
std::cout << " Taxa Aprendizado (eta): " << learning_rate << "\n";
}
/**
* @brief Constrói o vocabulário a partir de um corpus de texto.
* @param corpus Vetor de sentenças, onde cada sentença é um vetor de palavras (strings).
*/
void buildVocabulary(const std::vector<std::vector<std::string>>& corpus) {
std::cout << "Construindo vocabulário...\n";
std::unordered_map<std::string, long long> word_counts;
total_words = 0;
// Contar ocorrências
for (const auto& sentence : corpus) {
for (const auto& word : sentence) {
word_counts[word]++;
total_words++;
}
}
// Verificar se o corpus é válido
if (word_counts.empty()) {
std::cerr << "Erro: Corpus vazio ou inválido. Vocabulário não pode ser construído.\n";
return;
}
std::cout << " Total de palavras no corpus: " << total_words << "\n";
std::cout << " Número de palavras únicas: " << word_counts.size() << "\n";
// Construir vocabulário
vocabulary.clear();
word_to_index.clear();
int index = 0;
// Poderíamos adicionar filtragem por frequência mínima aqui se necessário
for (const auto& [word, count] : word_counts) {
Word w;
w.word = word;
w.count = count;
vocabulary.push_back(w);
word_to_index[word] = index++;
}
// Inicializar embeddings e tabela de amostragem negativa
initializeEmbeddings();
initNegativeTable();
std::cout << "Vocabulário construído com sucesso.\n";
}
/**
* @brief Treina o modelo SkipGram com Negative Sampling.
*
* Implementa o algoritmo SkipGram, onde para cada palavra-alvo tentamos
* prever as palavras em seu contexto. Usa Negative Sampling para aproximar
* o cálculo do softmax e tornar o treinamento eficiente.
*
* @param corpus Vetor de sentenças para treinamento.
* @param epochs Número de épocas de treinamento (padrão: 5).
*/
void trainSkipGram(const std::vector<std::vector<std::string>>& corpus, int epochs = 5) {
if (vocabulary.empty()) {
std::cerr << "Erro: Vocabulário não inicializado. Execute buildVocabulary primeiro.\n";
return;
}
std::cout << "Iniciando treinamento SkipGram por " << epochs << " épocas...\n";
float initial_lr = learning_rate;
words_processed = 0;
long long total_training_words = total_words * epochs;
for (int epoch = 0; epoch < epochs; ++epoch) {
long long epoch_words_processed = 0;
long long pairs_trained = 0;
for (const auto& sentence : corpus) {
for (size_t i = 0; i < sentence.size(); ++i) {
// Encontrar índice da palavra-alvo
auto target_it = word_to_index.find(sentence[i]);
if (target_it == word_to_index.end()) continue; // Palavra fora do vocabulário
int target_idx = target_it->second;
// Determinar janela de contexto dinâmica
int current_window = uniform_window(rng);
// Para cada posição de contexto no entorno da palavra-alvo
for (int j = -current_window; j <= current_window; ++j) {
if (j == 0) continue; // Pular a palavra-alvo
size_t context_pos = i + j;
// Verificar limites da sentença
if (context_pos < sentence.size()) { // size_t é sempre >= 0
auto context_it = word_to_index.find(sentence[context_pos]);
if (context_it != word_to_index.end()) {
int context_idx = context_it->second;
// Calcular taxa de aprendizado atual
float progress = static_cast<float>(words_processed) / total_training_words;
float current_lr = initial_lr * (1.0f - progress);
if (current_lr < min_learning_rate) current_lr = min_learning_rate;
// Treinar o par (target_idx, context_idx)
trainPair(target_idx, context_idx, current_lr);
pairs_trained++;
}
}
}
epoch_words_processed++;
words_processed++;
// Exibir progresso a cada 10000 palavras processadas
if (epoch_words_processed % 10000 == 0) {
float progress = static_cast<float>(words_processed) / total_training_words;
std::cout << "\rÉpoca " << epoch + 1 << "/" << epochs
<< ", Progresso: " << std::fixed << std::setprecision(2)
<< 100.0f * progress << "%, LR: " << learning_rate * (1.0f - progress)
<< std::flush;
}
}
}
std::cout << "\nÉpoca " << epoch + 1 << "/" << epochs
<< " completa. Pares treinados: " << pairs_trained << "\n";
}
std::cout << "Treinamento SkipGram concluído.\n";
}
/**
* @brief Salva os embeddings em um arquivo no formato texto Word2Vec.
* @param filename Nome do arquivo de saída.
* @note Salva apenas os vetores de entrada (v_w), que são tipicamente usados como embeddings.
*/
void saveEmbeddings(const std::string& filename) const {
std::cout << "Salvando embeddings em " << filename << "...\n";
std::ofstream file(filename);
if (!file.is_open()) {
std::cerr << "Erro ao abrir arquivo para escrita: " << filename << "\n";
return;
}
// Cabeçalho: número_de_palavras dimensão_vetor
file << vocabulary.size() << " " << vector_size << "\n";
// Linhas: palavra val1 val2 ... valN
for (const auto& word : vocabulary) {
file << word.word;
for (float val : word.vector) {
file << " " << std::fixed << std::setprecision(6) << val;
}
file << "\n";
}
file.close();
std::cout << "Embeddings salvos com sucesso.\n";
}
/**
* @brief Carrega embeddings pré-treinados de um arquivo.
* @param filename Nome do arquivo de entrada.
* @return True se o carregamento for bem-sucedido, false caso contrário.
*/
bool loadEmbeddings(const std::string& filename) {
std::cout << "Carregando embeddings de " << filename << "...\n";
std::ifstream file(filename);
if (!file.is_open()) {
std::cerr << "Erro ao abrir arquivo para leitura: " << filename << "\n";
return false;
}
size_t vocab_size;
int loaded_vector_size;
file >> vocab_size >> loaded_vector_size;
// Verifica se a dimensão do vetor carregado é compatível
if (file.fail() || loaded_vector_size <= 0) {
std::cerr << "Erro ao ler cabeçalho do arquivo: " << filename << "\n";
return false;
}
std::cout << " Arquivo contém " << vocab_size << " palavras com dimensão " << loaded_vector_size << ".\n";
// Ajustar dimensão do modelo se necessário
if (loaded_vector_size != vector_size) {
std::cout << " Aviso: Dimensão do vetor no arquivo (" << loaded_vector_size
<< ") difere da configuração do modelo (" << vector_size
<< "). Ajustando modelo para " << loaded_vector_size << ".\n";
vector_size = loaded_vector_size;
}
vocabulary.clear();
word_to_index.clear();
vocabulary.reserve(vocab_size);
for (size_t i = 0; i < vocab_size; ++i) {
Word w;
file >> w.word;
if (file.fail()) {
std::cerr << "Erro ao ler palavra no índice " << i << " do arquivo.\n";
return false;
}
w.vector.resize(vector_size);
for (int j = 0; j < vector_size; ++j) {
file >> w.vector[j];
if (file.fail()) {
std::cerr << "Erro ao ler valor do vetor para a palavra '" << w.word << "' no índice " << j << ".\n";
return false;
}
}
w.count = 1; // Contagem desconhecida ao carregar
vocabulary.push_back(w);
word_to_index[w.word] = i;
}
file.close();
// Reinicializar tabelas e pesos de saída para permitir treinamento adicional
initExpTable();
output_weights.resize(vocabulary.size(), std::vector<float>(vector_size, 0.0f));
total_words = vocabulary.size(); // Estimativa grosseira
std::cout << "Embeddings carregados com sucesso.\n";
return true;
}
/**
* @brief Encontra as palavras com maior grau de similaridade a uma palavra dada.
* @param word Palavra de consulta.
* @param top_n Número de palavras similares a retornar (padrão: 10).
* @return Vetor de pares (palavra, similaridade), ordenado por similaridade decrescente.
*/
std::vector<std::pair<std::string, float>> findSimilar(const std::string& word, int top_n = 10) const {
auto it = word_to_index.find(word);
if (it == word_to_index.end()) {
std::cerr << "Aviso: Palavra '" << word << "' não encontrada no vocabulário.\n";
return {};
}
int word_idx = it->second;
const auto& word_vector = vocabulary[word_idx].vector;
std::vector<std::pair<std::string, float>> similarities;
similarities.reserve(vocabulary.size());
for (size_t i = 0; i < vocabulary.size(); ++i) {
if (i == word_idx) continue; // Não comparar a palavra consigo mesma
float similarity = cosineSimilarity(word_vector, vocabulary[i].vector);
similarities.emplace_back(vocabulary[i].word, similarity);
}
// Ordenar por similaridade decrescente
std::sort(similarities.begin(), similarities.end(),
[](const auto& a, const auto& b) { return a.second > b.second; });
// Retornar os top_n resultados
if (similarities.size() > static_cast<size_t>(top_n)) {
similarities.resize(top_n);
}
return similarities;
}
/**
* @brief Calcula a similaridade de cosseno entre dois vetores.
* @param a Primeiro vetor.
* @param b Segundo vetor.
* @return Valor da similaridade de cosseno [-1, 1]. Retorna 0 se uma das normas for zero.
*/
float cosineSimilarity(const std::vector<float>& a, const std::vector<float>& b) const {
if (a.size() != b.size() || a.empty()) {
return 0.0f; // Vetores incompatíveis ou vazios
}
float dot_product = 0.0f;
float norm_a = 0.0f;
float norm_b = 0.0f;
for (size_t i = 0; i < a.size(); ++i) {
dot_product += a[i] * b[i];
norm_a += a[i] * a[i];
norm_b += b[i] * b[i];
}
// Evitar divisão por zero
if (norm_a <= 0.0f || norm_b <= 0.0f) {
return 0.0f;
}
return dot_product / (std::sqrt(norm_a) * std::sqrt(norm_b));
}
/**
* @brief Realiza operações de analogia vetorial (a - b + c ≈ ?).
* @param a Primeira palavra positiva.
* @param b Palavra negativa.
* @param c Segunda palavra positiva.
* @param top_n Número de resultados a retornar (padrão: 5).
* @return Vetor de pares (palavra, similaridade).
*/
std::vector<std::pair<std::string, float>> analogy(const std::string& a,
const std::string& b,
const std::string& c,
int top_n = 5) const {
auto it_a = word_to_index.find(a);
auto it_b = word_to_index.find(b);
auto it_c = word_to_index.find(c);
if (it_a == word_to_index.end() || it_b == word_to_index.end() || it_c == word_to_index.end()) {
std::cerr << "Aviso: Uma ou mais palavras da analogia (" << a << ", " << b << ", " << c << ") não encontradas no vocabulário.\n";
return {};
}
const auto& vec_a = vocabulary[it_a->second].vector;
const auto& vec_b = vocabulary[it_b->second].vector;
const auto& vec_c = vocabulary[it_c->second].vector;
std::vector<float> result_vec(vector_size);
for (int i = 0; i < vector_size; ++i) {
result_vec[i] = vec_a[i] - vec_b[i] + vec_c[i];
}
// Normalizar o vetor resultante
float norm = 0.0f;
for (float val : result_vec) {
norm += val * val;
}
norm = std::sqrt(norm);
if (norm > 0.0f) {
for (float& val : result_vec) {
val /= norm;
}
}
// Encontrar palavras mais similares ao vetor resultante
std::vector<std::pair<std::string, float>> similarities;
similarities.reserve(vocabulary.size());
for (size_t i = 0; i < vocabulary.size(); ++i) {
// Não incluir as palavras de entrada na lista de resultados
if (i == it_a->second || i == it_b->second || i == it_c->second) {
continue;
}
float similarity = cosineSimilarity(result_vec, vocabulary[i].vector);
similarities.emplace_back(vocabulary[i].word, similarity);
}
// Ordenar e retornar top_n
std::sort(similarities.begin(), similarities.end(),
[](const auto& x, const auto& y) { return x.second > y.second; });
if (similarities.size() > static_cast<size_t>(top_n)) {
similarities.resize(top_n);
}
return similarities;
}
/**
* @brief Retorna o vetor embedding de uma palavra.
* @param word Palavra de consulta.
* @return Vetor de embedding. Retorna um vetor de zeros se a palavra não for encontrada.
*/
std::vector<float> getWordVector(const std::string& word) const {
auto it = word_to_index.find(word);
if (it == word_to_index.end()) {
std::cerr << "Aviso: Palavra '" << word << "' não encontrada no vocabulário.\n";
return std::vector<float>(vector_size, 0.0f);
}
return vocabulary[it->second].vector;
}
};
/**
* @brief Função principal que demonstra o uso da classe Word2Vec_SkipGram.
*
* Este programa cria um modelo Word2Vec SkipGram, constrói o vocabulário a partir de um corpus
* simplificado, treina o modelo com SkipGram e Negative Sampling, e demonstra funcionalidades
* como busca de palavras similares, operações de analogia e salvamento de embeddings.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
// Configurar o console para UTF-8 (Específico do Windows)
#ifdef _WIN32
SetConsoleOutputCP(CP_UTF8);
std::cout << "Console configurado para UTF-8.\n";
#endif
// Corpus simplificado (o mesmo do exemplo anterior)
std::vector<std::vector<std::string>> corpus = {
{"o", "gato", "preto", "corre", "pelo", "jardim"},
{"o", "cachorro", "late", "para", "o", "gato"},
{"gatos", "e", "cachorros", "são", "animais", "domésticos"},
{"muitas", "pessoas", "gostam", "de", "ter", "um", "animal", "de", "estimação"},
{"os", "gatos", "gostam", "de", "dormir", "durante", "o", "dia"},
{"os", "cachorros", "precisam", "passear", "todos", "os", "dias"}
};
std::cout << "Corpus de exemplo carregado com " << corpus.size() << " sentenças.\n";
// --- Criar e Treinar Modelo SkipGram ---
// Usar parâmetros menores para o exemplo pequeno: dimensão 20, janela 2, 5 amostras negativas
Word2Vec_SkipGram model(20, 2, 5, 0.05f);
// Medir Construção do Vocabulário
auto start_vocab = std::chrono::high_resolution_clock::now();
// Construir vocabulário a partir do corpus
model.buildVocabulary(corpus);
// Calcular o tempo de construção do vocabulário
auto end_vocab = std::chrono::high_resolution_clock::now();
auto duration_vocab = std::chrono::duration_cast<std::chrono::nanoseconds>(end_vocab - start_vocab);
std::cout << "Tempo de construção do vocabulário: " << duration_vocab.count() << " ns\n";
// Medir Treinamento
int epochs_count = 100;
auto start_train = std::chrono::high_resolution_clock::now();
// Treinar o modelo SkipGram com Negative Sampling
model.trainSkipGram(corpus, epochs_count);
auto end_train = std::chrono::high_resolution_clock::now();
auto duration_train = std::chrono::duration_cast<std::chrono::nanoseconds>(end_train - start_train);
std::cout << "Tempo de treinamento (" << epochs_count << " épocas): " << duration_train.count() << " ns\n";
// --- Usar o Modelo Treinado ---
// Encontrar palavras similares a 'gato'
std::cout << "\n--- Palavras similares a 'gato' ---\n";
auto similar_to_cat = model.findSimilar("gato", 5); // Top 5
if (similar_to_cat.empty()) {
std::cout << "Nenhuma palavra similar encontrada (ou 'gato' não está no vocabulário).\n";
}
else {
for (const auto& [word, similarity] : similar_to_cat) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
}
}
// Encontrar palavras similares a 'cachorro'
std::cout << "\n--- Palavras similares a 'cachorro' ---\n";
auto similar_to_dog = model.findSimilar("cachorro", 5); // Top 5
if (similar_to_dog.empty()) {
std::cout << "Nenhuma palavra similar encontrada (ou 'cachorro' não está no vocabulário).\n";
}
else {
for (const auto& [word, similarity] : similar_to_dog) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
}
}
// Testar analogia: gato - gatos + cachorro ≈ cachorros ?
std::cout << "\n--- Analogia: gato está para gatos assim como cachorro está para...? ---\n";
auto analogy_results = model.analogy("gato", "gatos", "cachorro", 3); // Top 3
if (analogy_results.empty()) {
std::cout << "Não foi possível calcular a analogia (palavras ausentes ou vocabulário pequeno).\n";
}
else {
for (const auto& [word, similarity] : analogy_results) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(4) << similarity << "\n";
}
// Esperado: 'cachorros' se o treino foi bom o suficiente
}
// Obter vetor de uma palavra específica
std::cout << "\n--- Vetor da palavra 'animal' ---\n";
std::vector<float> vec_animal = model.getWordVector("animal");
if (vec_animal != std::vector<float>(20, 0.0f)) { // Compara com vetor de zeros
std::cout << " [";
for (size_t i = 0; i < vec_animal.size(); ++i) {
std::cout << std::fixed << std::setprecision(3) << vec_animal[i] << (i == vec_animal.size() - 1 ? "" : ", ");
}
std::cout << "]\n";
}
else {
std::cout << " Palavra 'animal' não encontrada no vocabulário.\n";
}
// Salvar os embeddings resultantes
model.saveEmbeddings("SkipGram_word_embeddings.txt");
std::cout << "\nExecução concluída.\n";
return 0;
}
Hierarchical Softmax
Uma alternativa ao Negative Sampling é o Hierarchical Softmax, que usa uma árvore binária de Huffman para representar o vocabulário, onde as palavras mais frequentes ficam mais próximas da raiz. Cada palavra é uma folha da árvore, e o caminho da raiz até essa folha define uma sequência de decisões binárias.
A probabilidade de uma palavra é calculada como o produto das probabilidades de cada nó ao longo do caminho da raiz até a folha:
\[p(w \vert w_I) = \prod_{j=1}^{L(w)-1} \sigma([[n(w,j+1) = ch(n(w,j))]] \cdot v'_{n(w,j)}v_{w_I})\]Na qual:
- $L(w)$ é o comprimento do caminho até $w$;
- $n(w,j)$ é o $j$-ésimo nó no caminho;
- $ch(n)$ é o filho esquerdo de $n$;
- $[[x]]$ é $1$ se $x$ é verdadeiro, $-1$ caso contrário.
A complexidade computacional é reduzida para $O(\log \vert V \vert )$, o que representa uma melhoria significativa, especialmente para vocabulários extremamente grandes.
Comparação entre CBoW e SkipGram
Ambos os algoritmos, CBoW e SkipGram, geram embeddings de alta qualidade, mas apresentam características e desempenhos distintos dependendo do cenário de aplicação:
| Característica | CBoW | SkipGram |
|---|---|---|
| Objetivo | Prever palavra-alvo a partir do contexto | Prever palavras de contexto a partir da palavra-alvo |
| Qualidade para palavras frequentes | Superior, devido ao efeito de suavização | Bom, mas pode ser menos preciso que CBoW |
| Qualidade para palavras raras | Inferior, tende a subestimar palavras raras | Superior, cada ocorrência gera múltiplos exemplos de treinamento |
Referências
BAHDANAU, D.; CHO, K.; BENGIO, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In: INTERNATIONAL CONFERENCE ON LEARNING REPRESENTATIONS (ICLR), 3., 2015, San Diego. Proceedings […]. San Diego: ICLR, 2015.
BISHOP, C. M. Pattern Recognition and Machine Learning. New York: Springer, 2006.
BOJANOWSKI, P. et al. Enriching Word Vectors with Subword Information. arXiv:1607.04606, 2016.
BOJANOWSKI, P.; GRAVE, E.; JOULIN, A.; MIKOLOV, T. Enriching Word Vectors with Subword Information. Transactions of the Association for Computational Linguistics, v. 5, p. 135-146, 2017.
FIRTH, J. R. A Synopsis of Linguistic Theory, 1930-55. In: STUDIES IN LINGUISTIC ANALYSIS. Oxford: Blackwell, 1957. p. 1-31.
GOODFELLOW, I.; BENGIO, Y.; COURVILLE, A. Deep Learning. Cambridge: MIT Press, 2016.
HARRIS, Z. S. Distributional Structure. Word, v. 10, n. 2-3, p. 146-162, 1954.
HOCHREITER, S.; SCHMIDHUBER, J. Long Short-Term Memory. Neural Computation, v. 9, n. 8, p. 1735-1780, 1997.
JOULIN, A. et al. Bag of Tricks for Efficient Text Classification. arXiv:1607.01759, 2016.
MANNING, C. D.; RAGHAVAN, P.; SCHÜTZE, H. Introduction to Information Retrieval. Cambridge: Cambridge University Press, 2008.
MIKOLOV, T. et al. Distributed Representations of Words and Phrases and their Compositionality. Advances in Neural Information Processing Systems, v. 26, 2013.
MIKOLOV, T.; CHEN, K.; CORRADO, G.; DEAN, J. Efficient Estimation of Word Representations in Vector Space. In: INTERNATIONAL CONFERENCE ON LEARNING REPRESENTATIONS (ICLR), 2013, Scottsdale. Proceedings […]. Scottsdale: ICLR, 2013.
MIKOLOV, T.; SUTSKEVER, I.; CHEN, K.; CORRADO, G.; DEAN, J. Distributed Representations of Words and Phrases and their Compositionality. In: ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS (NIPS), 26., 2013, Lake Tahoe. Proceedings […]. Lake Tahoe: NIPS, 2013, p. 3111-3119.
MIKOLOV, T.; YIH, W.; ZWEIG, G. Linguistic Regularities in Continuous Space Word Representations. In: NORTH AMERICAN CHAPTER OF THE ASSOCIATION FOR COMPUTATIONAL LINGUISTICS: HUMAN LANGUAGE TECHNOLOGIES (NAACL-HLT), 2013, Atlanta. Proceedings […]. Atlanta: ACL, 2013, p. 746-751.
PENNINGTON, J.; SOCHER, R.; MANNING, C. GloVe: Global Vectors for Word Representation. In: CONFERENCE ON EMPIRICAL METHODS IN NATURAL LANGUAGE PROCESSING (EMNLP), 2014, Doha. Proceedings […]. Doha: ACL, 2014, p. 1532-1543.
ROSS, S. M. Introduction to Probability Models. 13. ed. Cambridge: Academic Press, 2023.
VASWANI, A.; SHAZEER, N.; PARMAR, N.; USZKOREIT, J.; JONES, L.; GOMEZ, A. N.; KAISER, Ł.; POLOSUKHIN, I. Attention is all you need. In: ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS, 30., 2017, Long Beach. Proceedings […]. Long Beach: NIPS, 2017. p. 5998-6008.
