Transformers- Desvendando a Modelagem de Sequências
Modelando Sequencias - Além da Frequência de Termos
Nos artigos anteriores, 1, 2 e 3, exploramos os fundamentos matemáticos e os algoritmos inocentes de vetorização para textos. Vimos como representar palavras e documentos como vetores, mas também percebemos que essas representações, como TF-IDF, perdem significado semântico.
A atenta leitora deve ter percebido, ao longo de toda a sua vida, que a linguagem natural parece seguir estruturas sequenciais. A posição de uma palavra em uma frase é importante para a construção do significado. A frase “O cachorro mordeu o homem” é muito diferente da frase “O homem mordeu o cachorro”, apesar de usarem as mesmas palavras.
Neste artigo, a esforçada leitora adentrará os mares de incerteza, probabilidades e sequências.
Começaremos com as abordagens probabilísticas clássicas, as Cadeias de Markov, intimamente relacionadas aos modelos N-gram, para entender como a dependência local, a relação entre uma palavra e seus vizinhos, pode ser modelada matematicamente. Essa compreensão nos levará a explorar mecanismos mais poderosos, construindo a intuição necessária para entender conceitos como o conceito de atenção, que revolucionou o campo do processamento de linguagem natural e é a espinha dorsal dos Transformers. Embora existam outros paradigmas importantes para modelagem sequencial, como as Redes Neurais Recorrentes (RNNs, LSTMs, GRUs), nosso foco aqui será traçar um caminho específico que nos levará diretamente aos fundamentos conceituais dos Transformers.
Antes dosTransformersdominarem o cenário, as Redes Neurais Recorrentes (RNNs) e suas variantes eram a principal escolha para modelagem de sequências. Entender suas ideias básicas ajuda a contextualizar a evolução para a atenção e os Transformers.
RNNs (Redes Neurais Recorrentes): são redes projetadas para dados sequenciais. A ideia chave é a recorrência: a saída em um passo de tempo $t$ depende não só da entrada atual $x_t$, mas também de uma “memória” ou estado oculto $h_{t-1}$ do passo anterior. A atualização pode ser representada como $h_t = f(W_{hh}h_{t-1} + W_{xh}x_t + b_h)$, onde $f$ é uma não-linearidade, como $\tanh$. O problema principal das RNNs simples é o desvanecimento ou explosão de gradientes durante o treinamento, dificultando o aprendizado de dependências de longo prazo.
LSTMs (Long Short-Term Memory): foram criadas para resolver o problema dos gradientes das RNNs. Introduzem uma célula de memória interna ($c_t$) que pode manter informações por longos períodos. O fluxo de informação para dentro e fora desta célula, e para o estado oculto ($h_t$), é controlado por três portões (gates) aprendíveis:
- Portão de Esquecimento ($f_t$): decide qual informação jogar fora da célula de memória.
- Portão de Entrada ($i_t$): decide quais novas informações armazenar na célula de memória.
- Portão de Saída ($o_t$): decide qual parte da célula de memória expor como estado oculto $h_t$. Isso permite que LSTMs capturem dependências de longo alcance de forma muito mais eficaz.
- GRUs (Gated Recurrent Units): São uma variação da LSTM, também projetada para lidar com dependências longas, mas com uma arquitetura um pouco mais simples. Elas combinam o estado da célula e o estado oculto e usam apenas dois portões:
- Portão de Atualização ($z_t$): Similar a uma combinação dos portões de esquecimento e entrada da LSTM, decidindo o quanto manter da memória antiga e o quanto adicionar da nova informação candidata.
- Portão de Reset ($r_t$): Decide o quanto “esquecer” da memória passada ao calcular a nova informação candidata. GRUs frequentemente apresentam desempenho comparável às LSTMs, mas com menos parâmetros, o que pode ser vantajoso em alguns cenários.
Tanto LSTMs quanto GRUs foram, e ainda são, muito importantes, mas sua natureza inerentemente sequencial, processar um passo de cada vez, limita a paralelização, uma das principais vantagens introduzidas pela arquitetura baseada puramente em atenção dos Transformers.
Modelo N-gram: A Perspectiva Markoviana (Ordem 1)
O termo N-gram no contexto dosTransformers(e em processamento de linguagem natural, ou NLP, em geral) refere-se a uma sequência contígua de n itens (geralmente palavras, caracteres ou tokens) extraída de um texto. É uma técnica usada para capturar informações contextuais ou padrões locais em uma sequência de dados. Neste caso, temos:
- Unigram (1-gram): Um único item (ex.: “gato”).
- Bigram (2-gram): Dois itens consecutivos (ex.: “gato preto”).
- Trigram (3-gram): Três itens consecutivos (ex.: “gato preto corre”).
O $N$ em N-gram indica o tamanho da sequência a ser considerada. Vamos modelar sequências de N-grams.
Uma das formas mais intuitivas de modelar sequências é assumir que o próximo elemento depende apenas de um número fixo de elementos anteriores. A abordagem mais simples é a Cadeia de Markov de Primeira Ordem.
Cadeias de Markov: cadeias de Markov são modelos probabilísticos usados para descrever sequências de eventos ou estados, onde a probabilidade de cada evento depende apenas do estado anterior, e não de toda a sequência de eventos que o precedeu. Essa propriedade é chamada de “propriedade de Markov” ou “memória de um passo”. Formalmente:
Uma cadeia de Markov é definida por um conjunto de estados (ex.: palavras, condições climáticas, etc.) e uma matriz de transição, que indica a probabilidade de passar de um estado para outro. Por exemplo, em um modelo de linguagem, se o termo atual é “gato”, a probabilidade da próxima palavra (como “preto” ou “corre”) é calculada com base apenas no termo “gato”, ignorando palavras anteriores.
Imagine um modelo de clima com dois estados: “sol” e “chuva”.
- Se hoje está “sol”, há 70% de chance de continuar “sol” amanhã e 30% de chance de “chuva”.
- Se hoje está “chuva”, há 50% de chance de “sol” e 50% de “chuva”.
Esse tipo de comportamento pode ser modelado por uma cadeia de Markov.
Cadeias de Markov são usadas em áreas como:
- Processamento de linguagem natural: aqui estamos nós. na previsão de palavras em modelos simples;
- Análise de séries temporais: previsão do tempo;
- Jogos e simulações: geração de comportamentos aleatórios.
No modelo N-gram, vamos assumir que a probabilidade de ocorrência de um termo depende apenas do termo anterior, uma característica conhecida como Propriedade de Markov. Nos modelos N-grams, isso se traduz no cálculo da probabilidade de um termo com base no termo imediatamente anterior.
Vamos tentar entender este processo, juntos, usando um corpus simples. Para tal, a criativa leitora pode imaginar que estamos desenvolvendo uma interface de linguagem natural, capaz de entender apenas três comandos específicos, dados nos seguintes documentos:
Mostre-me meus diretórios, por favor.;Mostre-me meus arquivos, por favor.;Mostre-me minhas fotos, por favor..
Primeiro, padronizamos os documentos (minúsculas, sem pontuação) e listamos todos os bigramas:
- $D_1$:
mostre me meus diretórios por favor-> (mostre, me), (me, meus), (meus, diretórios), (diretórios, por), (por, favor) - $D_2$:
mostre me meus arquivos por favor-> (mostre, me), (me, meus), (meus, arquivos), (arquivos, por), (por, favor) - $D_3$:
mostre me minhas fotos por favor-> (mostre, me), (me, minhas), (minhas, fotos), (fotos, por), (por, favor)
Nesta interface, nosso vocabulário $V$ tem cardinalidade $9$ e será dado por:
\[V = \{\text{mostre}, \text{me}, \text{meus}, \text{minhas}, \text{diretórios}, \text{arquivos}, \text{fotos}, \text{por}, \text{favor}\}\]Podemos representar as transições prováveis entre palavras com uma matriz de transição, $T$. Nesta matriz, cada linha e coluna corresponderá a uma palavra do vocabulário $V = {v_1, \dots, v_9}$. Assim sendo, uma entrada $T_{ij}$ da matriz indica a probabilidade de que a próxima palavra seja $v_j$, dado que a palavra atual é $v_i$. Formalmente, teremos:
\[T_{ij} = P(\text{próxima palavra} = v_j \vert \text{palavra atual} = v_i)\]Neste contexto que criamos, teremos que calcular as probabilidades de transição usando exclusivamente as três frases que definimos na nossa interface, assumindo que cada uma destas frases tem exatamente a mesma probabilidade de ocorrência, $1/3$. Estamos considerando esta distribuição de probabilidade de ocorrência das frases para manter o modelo simples.
Para o cálculo destas probabilidades usaremos a probabilidade condicional, dada por:
\[P(\text{próxima palavra} \vert \text{palavra atual)} = (\text{Número de vezes que a "próxima palavra" segue a "palavra atual" nas frases}) / (\text{Número total de vezes que a "palavra atual" aparece nas frases})\]Sendo assim, teremos:
-
Após “mostre”: sempre seguida por “me”. A palavra “mostre” aparece $3$ vezes no total (uma vez em cada frase). Em todas as $3$ vezes, a palavra seguinte é “me”.
\[P(\text{me} \vert \text{mostre}) = \frac{3}{3} = 1\]A probabilidade de qualquer outra palavra seguir “mostre” é $0$, pois isso nunca acontece nas frases que definem nossa interface.
-
Após “me”: é seguida por “meus” nas frases $1$ e $2$, e por “minhas” na frase $3$.
A palavra “me” aparece $3$ vezes no total (uma vez em cada frase). Em $2$ dessas vezes (frases 1 e 2), a palavra seguinte é “meus”. Em $1$ dessas vezes (frase 3), a palavra seguinte é “minhas”.
\[P(\text{meus} \vert \text{me}) = \frac{2 \text{ ocorrências}}{3 \text{ total}} = \frac{2}{3} \approx 0.67\] \[P(\text{minhas} \vert \text{me}) = \frac{1 \text{ ocorrência}}{3 \text{ total}} = \frac{1}{3} \approx 0.33\]A soma das probabilidades $(2/3 + 1/3)$ é $1$. A probabilidade de qualquer outra palavra seguir “me” é $0$.
-
Após “meus”: é seguida por “diretórios” na frase $1$ e “arquivos” na frase $2$. Assumindo que, uma vez que “meus” foi dita, as continuações “diretórios” e “arquivos” são igualmente prováveis:
\[P(\text{diretórios} \vert \text{meus}) = \frac{1 \text{ ocorrência}}{2 \text{ total}} = 0.5\] \[P(\text{arquivos} \vert \text{meus}) = \frac{1 \text{ ocorrência}}{2 \text{ total}} = 0.5\] \[P(\text{fotos} \vert \text{meus}) = 0\]isso porque “fotos” nunca segue “meus” nos documentos que determinam a interface que definimos antes.
-
Após “minhas”: sempre seguida por “fotos” (frase 3).
\[P(\text{fotos} \vert \text{minhas}) = 1\] -
Após “diretórios”: Sempre seguida por “por” (frase 1).
\[P(\text{por} \vert \text{diretórios}) = 1\] -
Após “arquivos”: Sempre seguida por “por” (frase 2).
\[P(\text{por} \vert \text{arquivos}) = 1\] -
Após “fotos”: Sempre seguida por “por” (frase 3).
\[P(\text{por} \vert \text{fotos}) = 1\] -
Após “por”: Sempre seguida por “favor” (todas as frases).
\[P(\text{favor} \vert \text{por}) = 1\] -
Após “favor”: É o fim da frase, nenhuma palavra segue.
A palavra “favor” aparece $3$ vezes no total (uma vez em cada frase). Em nenhuma das vezes ela é seguida por outra palavra (é o fim da frase). Portanto, a contagem de “favor” seguida por qualquer palavra (v_j) é $0$. Logo, teremos:
\[P(v_j \vert \text{favor}) = 0\]para todo $v_j$.
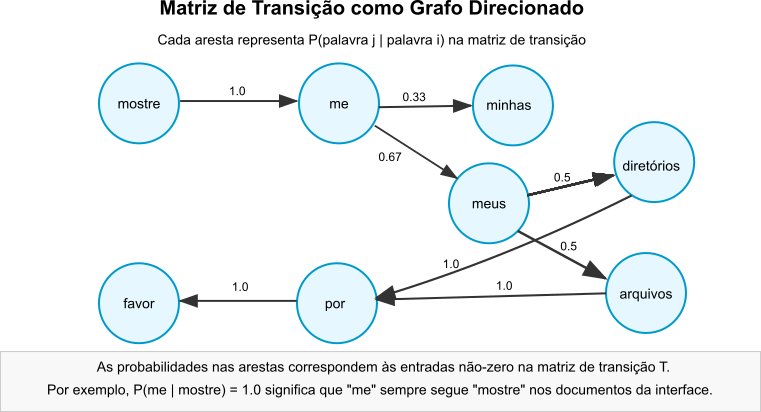 Figura 1: Exemplo de transições entre palavras em um modelo de linguagem baseado em Cadeias de Markov.
Figura 1: Exemplo de transições entre palavras em um modelo de linguagem baseado em Cadeias de Markov.
A matriz de transição $T$ que reflete estas probabilidades calculadas a partir das três frases será:
| Palavra Atual | mostre | me | meus | minhas | diretórios | arquivos | fotos | por | favor | Soma da Linha |
|---|---|---|---|---|---|---|---|---|---|---|
| mostre | 0 | 1.00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 |
| me | 0 | 0 | 0.67 | 0.33 | 0 | 0 | 0 | 0 | 0 | 1.00 |
| meus | 0 | 0 | 0 | 0 | 0.50 | 0.50 | 0.00 | 0 | 0 | 1.00 |
| minhas | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | 0 | 0 | 1.00 |
| diretórios | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | 0 | 1.00 |
| arquivos | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | 0 | 1.00 |
| fotos | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | 0 | 1.00 |
| por | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | 1.00 |
| favor | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.00 |
Tabela 1: Matriz de transição $T$ derivada das três frases de exemplo.
Nesta matriz $T$, a linha $i$ representa a distribuição de probabilidade da próxima palavra, dado que a palavra atual é $v_i \in V$. Cada entrada $T_{ij}$ satisfaz a condição $0 \le T_{ij} \le 1$. A soma das probabilidades em cada linha é $1$. Exceto para a palavra final “favor”, que não transiciona para nenhuma outra.
A estrutura fixa das frases deste exemplo define a maioria das transições com probabilidade 0 ou 1. A incerteza, probabilidades entre 0 e 1, ocorre após “me”, levando a “meus” com $P \approx 0.67$ ou “minhas” com $P \approx 0.33$ e após “meus” (levando a “diretórios” com $P=0.5$ ou “arquivos” com $P=0.5$).
Para extrair a distribuição de probabilidade da próxima palavra após uma palavra específica, como “meus”, podemos usar um vetor one-hot. O vetor $h_{\text{meus}}$ é um vetor linha com $1$ na posição correspondente à palavra “meus” e $0$ nas demais.
\[h_{\text{meus}} = [0, 0, 1, 0, 0, 0, 0, 0, 0]\]A multiplicação $h_{\text{meus}} \times T$ resulta em um vetor linha que contém a linha da matriz $T$ correspondente a “meus” será:
\[h_{\text{meus}} \times T = [0, 0, 0, 0, 0.50, 0.50, 0.00, 0, 0]\]Este vetor resultante indica que, após “meus”, a probabilidade de ver “diretórios” é $0.50$ e “arquivos” é $0.50$, consistente com as frases de exemplo. Esta operação está sintetizada na Figura 2.
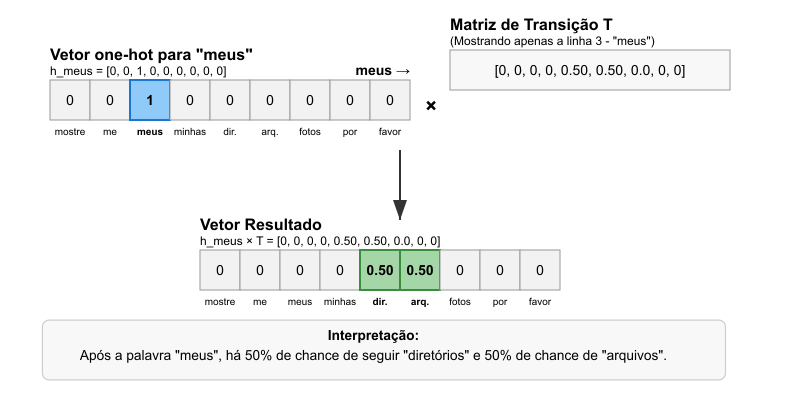 Figura 2: Extração das probabilidades de transição para a palavra “meus” usando um vetor one-hot e multiplicação de matrizes.
Figura 2: Extração das probabilidades de transição para a palavra “meus” usando um vetor one-hot e multiplicação de matrizes.
Para lembrar: quando realização a multiplicação de um vetor linha por uma matriz, usamos produtos escalares.
Quando multiplicamos um vetor linha $v$ de dimensão $1 \times n$ por uma matriz $M$ de dimensão $n \times m$, o resultado é um vetor linha $r$ de dimensão $1 \times m$.
No caso específico da multiplicação $h_{\text{meus}} \times T$:
- O vetor linha $h_{\text{meus}} = [0, 0, 1, 0, 0, 0, 0, 0, 0]$ tem dimensão $1 \times 9$;
- A matriz $T$ tem dimensão $9 \times 9$;
- O resultado $R$ terá dimensão $1 \times 9$.
Para cada elemento $j$ do vetor resultante $R$, calculamos o produto escalar entre o vetor linha $h_{\text{meus}}$ e a coluna $j$ da matriz $T$:
\[R_j = \sum_{i=1}^{9} h_{\text{meus},i} \times T_{i,j}\]Como o vetor $h_{\text{meus}}$ é um vetor one-hot com valor 1 apenas na posição 3, a maioria dos termos da soma acima será zero, e teremos:
\[R_j = 0 \times T_{1,j} + 0 \times T_{2,j} + 1 \times T_{3,j} + 0 \times T_{4,j} + ... + 0 \times T_{9,j} = T_{3,j}\]Isso significa que cada elemento $j$ do vetor resultante $R$ será igual ao elemento na posição $(3,j)$ da matriz $T$.
Em termos práticos, a multiplicação de um vetor one-hot por uma matriz resulta na extração da linha correspondente à posição do valor 1 no vetor one-hot. É por isso que o resultado final é simplesmente a terceira linha da matriz $T$:
\[R = [0, 0, 0, 0, 0.50, 0.50, 0.00, 0, 0]\]
Implementar esta operação em C++ é direto, especialmente se tivermos uma classe otimizada para operações com matrizes como é o cado da biblioteca Eigen:
#include <iostream> ///< Para entrada e saída padrão (std::cout).
#include <vector> ///< Para contêiner std::vector usado no armazenamento do vocabulário.
#include <string> ///< Para std::string, usado em palavras e mensagens.
#include <unordered_map> ///< Para std::unordered_map, usado no mapeamento de palavras para índices.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <Eigen/Dense> ///< Para a biblioteca Eigen, usada em operações com matrizes e vetores.
/**
* @class BigramModel
* @brief Uma classe para modelar transições de bigramas entre palavras usando uma matriz de transição.
*
* Esta classe constrói um vocabulário a partir de uma lista de palavras, cria uma matriz de transição
* com probabilidades condicionais P(w_t | w_{t-1}), e permite consultar as probabilidades da próxima
* palavra dado um termo inicial. Utiliza a biblioteca Eigen para operações matriciais e vetoriais.
*/
class BigramModel {
private:
std::vector<std::string> vocabulary; ///< Vocabulário ordenado de palavras.
std::unordered_map<std::string, int> termToIndex; ///< Mapeamento de palavras para índices no vocabulário.
Eigen::MatrixXd transitionMatrix; ///< Matriz de transição (NxN) com probabilidades P(w_t | w_{t-1}).
size_t vocabularySize; ///< Tamanho do vocabulário.
public:
/**
* @brief Construtor que inicializa o modelo com um vocabulário.
* @param vocab Vetor de strings contendo as palavras do vocabulário.
*/
BigramModel(const std::vector<std::string>& vocab) : vocabulary(vocab), vocabularySize(vocab.size()) {
// Inicializar o mapeamento de palavras para índices
for (size_t i = 0; i < vocabularySize; ++i) {
termToIndex[vocabulary[i]] = i;
}
// Inicializar a matriz de transição com zeros
transitionMatrix = Eigen::MatrixXd::Zero(vocabularySize, vocabularySize);
}
/**
* @brief Define a probabilidade de transição entre duas palavras.
* @param fromWord A palavra inicial (w_{t-1}).
* @param toWord A palavra seguinte (w_t).
* @param probability A probabilidade P(w_t | w_{t-1}).
*/
void setTransitionProbability(const std::string& fromWord, const std::string& toWord, double probability) {
auto fromIt = termToIndex.find(fromWord);
auto toIt = termToIndex.find(toWord);
if (fromIt != termToIndex.end() && toIt != termToIndex.end()) {
transitionMatrix(fromIt->second, toIt->second) = probability;
}
}
/**
* @brief Cria um vetor one-hot para uma palavra.
* @param word A palavra para a qual o vetor one-hot será criado.
* @return Vetor one-hot (Eigen::VectorXd) com 1.0 na posição da palavra e 0.0 nas demais. Retorna vetor de zeros se a palavra for desconhecida.
*/
Eigen::VectorXd createOneHotVector(const std::string& word) const {
Eigen::VectorXd oneHotVector = Eigen::VectorXd::Zero(vocabularySize);
auto it = termToIndex.find(word);
if (it != termToIndex.end()) {
oneHotVector(it->second) = 1.0;
}
return oneHotVector;
}
/**
* @brief Consulta as probabilidades da próxima palavra dado um termo inicial.
* @param word A palavra inicial (w_{t-1}).
* @return Vetor de probabilidades (Eigen::RowVectorXd) para a próxima palavra P(w_t | w_{t-1}).
*/
Eigen::RowVectorXd getNextWordProbabilities(const std::string& word) const {
Eigen::VectorXd oneHotVector = createOneHotVector(word);
return oneHotVector.transpose() * transitionMatrix;
}
/**
* @brief Exibe as probabilidades da próxima palavra dado um termo inicial.
* @param word A palavra inicial (w_{t-1}).
*/
void printNextWordProbabilities(const std::string& word) const {
Eigen::RowVectorXd probabilities = getNextWordProbabilities(word);
std::cout << "Probabilidades da próxima palavra após '" << word << "' (Modelo de 1ª Ordem / Bigramas):\n";
for (size_t i = 0; i < vocabularySize; ++i) {
if (probabilities(i) > 0) { // Mostrar apenas probabilidades não nulas
std::cout << " " << vocabulary[i] << ": " << std::fixed << std::setprecision(2) << probabilities(i) << "\n";
}
}
}
/**
* @brief Obtém o vocabulário do modelo.
* @return Referência constante ao vetor de strings do vocabulário.
*/
const std::vector<std::string>& getVocabulary() const {
return vocabulary;
}
};
/**
* @brief Função principal que demonstra o uso da classe BigramModel.
*
* Este programa cria um modelo de bigramas com um vocabulário predefinido, define probabilidades
* de transição para simular um modelo de linguagem simples, e consulta as probabilidades da próxima
* palavra após "meus" usando uma representação one-hot e a matriz de transição.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
// Definir o vocabulário
std::vector<std::string> vocabulary = {
"mostre", "me", "meus", "minhas", "diretórios", "arquivos", "fotos", "por", "favor"
};
// Criar e configurar o modelo de bigramas
BigramModel model(vocabulary);
// Definir as probabilidades de transição (P(w_t | w_{t-1}))
model.setTransitionProbability("mostre", "me", 1.0); // Após "mostre", sempre vem "me"
model.setTransitionProbability("me", "meus", 2.0/3.0); // Após "me", "meus" com 66.7%
model.setTransitionProbability("me", "minhas", 1.0/3.0); // Após "me", "minhas" com 33.3%
model.setTransitionProbability("meus", "diretórios", 0.5); // Após "meus", "diretórios" com 50%
model.setTransitionProbability("meus", "arquivos", 0.5); // Após "meus", "arquivos" com 50%
model.setTransitionProbability("minhas", "fotos", 1.0); // Após "minhas", sempre vem "fotos"
model.setTransitionProbability("diretórios", "por", 1.0); // Após "diretórios", sempre vem "por"
model.setTransitionProbability("arquivos", "por", 1.0); // Após "arquivos", sempre vem "por"
model.setTransitionProbability("fotos", "por", 1.0); // Após "fotos", sempre vem "por"
model.setTransitionProbability("por", "favor", 1.0); // Após "por", sempre vem "favor"
// Consultar e exibir as probabilidades da próxima palavra após "meus"
model.printNextWordProbabilities("meus");
return 0;
}
Vetorização Probabilística usando Modelos N-gram
Em um modelo N-gram probabilístico, cada documento $D$ é representado por sua própria matriz de transição $T_D$, na qual cada elemento $T_D(i,j)$ indica a probabilidade condicional de transição da palavra $i$ para a palavra $j$ especificamente no documento $D$:
\[T_D(i,j) = P(w_j | w_i, D) = \frac{\text{count}(w_i, w_j, D)}{\text{count}(w_i, D)}\]Neste caso, temos:
- $\text{count}(w_i, w_j, D)$ é o número de vezes que a sequência $w_i w_j$ aparece no documento $D$;
- $\text{count}(w_i, D)$ é o número total de ocorrências de $w_i$ no documento $D$.
Essa matriz de transição captura a assinatura probabilística do documento. Esta assinatura caracteriza um padrão único de como as palavras seguem umas às outras em um documento específico.
A vetorização usando o modelo N-gram pode ser descrito em $4$ etapas:
1. Construção da Matriz de Transição por Documento
Para cada documento em nosso corpus, construímos uma matriz de transição $T_D$ de tamanho $ \vert V \vert \times \vert V \vert $, onde $ \vert V \vert $ é um valor escalar que representa a cardinalidade do vocabulário. Esta matriz inicialmente conterá zeros e será preenchida conforme analisarmos as sequências de palavras, da seguinte forma:
- identifique todos os bigramas, pares de palavras adjacentes, em um documento;
- para cada bigrama $(w_i, w_j)$, incremente o contador da posição $(i,j)$ na matriz;
- Normalize cada linha da matriz dividindo cada entrada pelo total da linha;
Por exemplo, para o documento Mostre-me meus diretórios, por favor, a matriz terá entradas não-zero apenas para as transições que ocorrem neste documento específico:
- $P(\text{me} \vert \text{mostre}) = 1.0$
- $P(\text{meus} \vert \text{me}) = 1.0$
- $P(\text{diretórios} \vert \text{meus}) = 1.0$
- $P(\text{por} \vert \text{diretórios}) = 1.0$
- $P(\text{favor} \vert \text{por}) = 1.0$
A transição $P(\text{me} \vert \text{mostre})$ ocorre apenas uma vez no documento Mostre-me meus diretórios, por favor. O mesmo ocorre para todos os bigramas deste documento. Todas as outras probabilidades $P(w_j \vert w_i, D)$ são $0$. Os respectivos bigramas $(w_i, w_j)$ não ocorrem ou $w_i$ não ocorre, no caso da palavra “favor”, que nunca inicia um bigrama neste exemplo, então $P(\text{qualquer} \vert \text{favor}) = 0/1 = 0$.
A matriz de transição $T_D$ será:
\[T_D = \begin{array}{c|cccccc} & \textbf{mostre} & \textbf{me} & \textbf{meus} & \textbf{diretórios} & \textbf{por} & \textbf{favor} \\ \hline \textbf{mostre} & 0 & 1.0 & 0 & 0 & 0 & 0 \\ \textbf{me} & 0 & 0 & 1.0 & 0 & 0 & 0 \\ \textbf{meus} & 0 & 0 & 0 & 1.0 & 0 & 0 \\ \textbf{diretórios} & 0 & 0 & 0 & 0 & 1.0 & 0 \\ \textbf{por} & 0 & 0 & 0 & 0 & 0 & 1.0 \\ \textbf{favor} & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\]2. Compactação da Matriz em Vetor
Como as matrizes de transição são tipicamente esparsas, a maioria das entradas é zero, podemos compactá-las em vetores que contêm apenas informações relevantes. Existem várias abordagens para esta compactação:
-
Vetorização Completa: concatenar todas as probabilidades não-zero da matriz com seus respectivos índices:
\[\vec{v_d} = [i_1, j_1, p_1, i_2, j_2, p_2, ..., i_k, j_k, p_k]\]Neste caso, teremos: $(i_n, j_n, p_n)$ representa uma transição da palavra $i_n$ para a palavra $j_n$ com probabilidade $p_n$. Este processo tem a vantagem de manter todas as transições, mas pode resultar em vetores muito longos e esparsos. Além disso, O formato $[índice_i, índice_j, probabilidade]$ não é um modelo de vetor característico maioria das bibliotecas usadas em machine learning. Estas bibliotecas geralmente esperam que cada posição no vetor corresponda a uma característica específica e fixa.
Para o exemplo do documento
Mostre-me meus diretórios, por favor, listamos todos os triplets $[i, j, p]$ onde $p > 0$:- Transição (mostre, me): $i=1, j=2, p=1.0$
- Transição (me, meus): $i=2, j=3, p=1.0$
- Transição (meus, diretórios): $i=3, j=4, p=1.0$
- Transição (diretórios, por): $i=4, j=5, p=1.0$
- Transição (por, favor): $i=5, j=6, p=1.0$
O vetor resultante será:
\[\vec{v_d} = [1, 2, 1.0, \quad 2, 3, 1.0, \quad 3, 4, 1.0, \quad 4, 5, 1.0, \quad 5, 6, 1.0]\]A atenta leitora deve notar que este vetor tem comprimento $5 \times 3 = 15$. Outro documento poderia ter um número diferente de transições não-nulas, gerando um vetor de comprimento diferente.
-
Vetorização por Transições Específicas: selecionar apenas as transições mais informativas ou discriminativas entre documentos:
\[\vec{v_d} = [P(w_j \vert w_i, d) \text{ para pares } (i,j) \text{ selecionados}]\]Esta abordagem reduz a dimensionalidade focando apenas nas transições que melhor distinguem diferentes classes de documentos. Normalmente resulta em vetores de comprimento fixo. Para isso, temos que garantir que o mesmo conjunto de transições seja usado para todos os documentos no corpus. Esta escolha irá criar um vetor no formato
[prob1, prob2, ...]. Um vetor de características fixas adequado às bibliotecas de machine learning. Além disso, esta técnica reduz a dimensionalidade, focando no que se acredita ser mais relevante.Por outro lado, esta técnica requer um passo adicional: a seleção das transições que seja interessantes para a tarefa de processamento de linguagem natural que estamos tentando implementar. Como selecionar essas transições (ex: as mais frequentes no corpus? as que têm maior poder discriminativo entre classes?) é um problema complexo em si. E sempre haverá uma escolha entre a quantidade de informação que se perde e a eficiência do modelo.
Para montar um vetor comprimido, precisamos escolher um conjunto fixo de transições $(i, j)$ para monitorar em todos os documentos. Podemos tentar usando um critério simples: as transições mais frequentes no corpus. Vamos usar o mesmo corpus que usamos para calcular a matriz de transição $T$.
- $D_1$:
mostre me meus diretórios por favor-> (mostre, me), (me, meus), (meus, diretórios), (diretórios, por), (por, favor) - $D_2$:
mostre me meus arquivos por favor-> (mostre, me), (me, meus), (meus, arquivos), (arquivos, por), (por, favor) - $D_3$:
mostre me minhas fotos por favor-> (mostre, me), (me, minhas), (minhas, fotos), (fotos, por), (por, favor)
Agora, podemos contar quantas vezes cada bigrama único aparece no corpus:
- (mostre, me): $3$ vezes;
- (por, favor): $3$ vezes;
- (me, meus): $2$ vezes;
- (meus, diretórios): $1$ vez;
- (diretórios, por): $1$ vez;
- (meus, arquivos): $1$ vez;
- (arquivos, por): $1$ vez;
- (me, minhas): $1$ vez;
- (minhas, fotos): $1$ vez;
- (fotos, por): $1$ vez.
A abordagem de Vetorização por Transições Específicas exige que escolhamos um conjunto fixo de transições $(w_i, w_j)$ que serão usadas como características para todos os documentos. Usando o critério das transições mais frequentes, selecionamos as transições com as maiores contagens no corpus. Neste caso, como o corpus é muito pequeno e simples, estamos fadados a pegar as $3$ transições mais frequentes:
- $t_1 = (\text{mostre, me})$ (Frequência: 3)
- $t_2 = (\text{por, favor})$ (Frequência: 3)
- $t_3 = (\text{me, meus})$ (Frequência: 2)
Este conjunto de $3$ transições definirá o nosso espaço vetorial. Ou seja, neste método, com esta escolha de seleção, cada documento no corpus será representado por um vetor de dimensão $3$.
Após selecionar um conjunto fixo dessas transições $T_{selecionadas} = {t_1, t_2, …, t_k}$, onde cada $t_m = (w_i, w_j)_m$, representamos cada documento $D$ por um vetor $\vec{v}_D$ de dimensão $k$. A $m$-ésima componente deste vetor será a probabilidade $P(w_j \vert w_i, D)$ da $m$-ésima transição selecionada $(w_i, w_j)_m$, calculada especificamente para o documento $D$:
\[\vec{v}_D = [ P(t_1 \vert D), P(t_2 \vert D), ..., P(t_k \vert D) ]\]Neste caso, temos: $P(t_m \vert D) = P( (w_j \vert w_i)_m \vert D ) = \frac{\text{count}((w_i, w_j)_m, D)}{\text{count}(w_i, D)}$. Se uma transição selecionada $t_m$ não ocorrer no documento $D$, ou se $w_i$ não ocorrer, então $P(t_m \vert D) = 0$.
Essa abordagem garante que todos os documentos sejam representados por vetores de mesma dimensão ($k$), adequados para algoritmos de Machine Learning, focando nas sequências de palavras consideradas mais relevantes (neste caso, as mais comuns) no contexto geral do corpus.
Assim, no Documento $D_1$:
mostre me meus diretórios por favorteremos: $t_1 = (\text{mostre, me})$, $t_2 = (\text{por, favor})$, $t_3 = (\text{me, meus})$. Calculamos as probabilidades para $D_1$:-
Para $t_1 = (\text{mostre, me})$:
- $\text{count}(\text{mostre, me}, D_1) = 1$;
- $\text{count}(\text{mostre}, D_1) = 1$;
- $P(t_1 \vert D_1) = P(\text{me} \vert \text{mostre}, D_1) = 1 / 1 = 1.0$.
-
Para $t_2 = (\text{por, favor})$:
- $\text{count}(\text{por, favor}, D_1) = 1$;
- $\text{count}(\text{por}, D_1) = 1$;
- $P(t_2 \vert D_1) = P(\text{favor} \vert \text{por}, D_1) = 1 / 1 = 1.0$.
-
Para $t_3 = (\text{me, meus})$:
- $\text{count}(\text{me, meus}, D_1) = 1$;
- $\text{count}(\text{me}, D_1) = 1$;
- $P(t_3 \vert D_1) = P(\text{meus} \vert \text{me}, D_1) = 1 / 1 = 1.0$.
Portanto, o vetor compactado para o Documento 1, usando as 3 transições mais frequentes do corpus para definir as 0características importantes, será:
\[\vec{v}_{D1} = [ P(t_1 \vert D_1), P(t_2 \vert D_1), P(t_3 \vert D_1) ] = [1.0, 1.0, 1.0]\]O mesmo processo deve ser aplicado aos outros documentos do corpus.
- $D_1$:
3. Normalização do Vetor de Características
Para garantir comparabilidade entre documentos de diferentes tamanhos, é comum normalizar o vetor resultante $\vec{v_d}$. Vetores mais longos, em termos de norma, poderiam dominar as medidas de similaridade ou distância simplesmente por representarem documentos maiores ou com mais ocorrências das transições selecionadas. A normalização ajusta a escala dos vetores. A normalização mais comum é a Norma Euclidiana (L2):
\[\vec{v_d}^{\text{norm}} = \frac{\vec{v_d}}{ \vert \vec{v_d} \vert _2}\]Neste caso,
\[\vert \vec{v_d} \vert _2\]representa a norma Euclidiana do vetor, dada pela raiz quadrada da soma dos quadrados de seus elementos:
\[\vert \vec{v_d} \vert _2 = \sqrt{\sum_{i} v_{d,i}^2}\]Após a normalização L2, o vetor terá um comprimento, magnitude, igual a $1$.
Vamos aplicar a normalização ao vetor $\vec{v}_{D1}$ que obtivemos para o documento $1$ usando a Vetorização por Transições Específicas:
\[\vec{v}_{D1} = [1.0, 1.0, 1.0]\]Primeiro, calculamos a norma Euclidiana (L2) deste vetor:
\[\vert \vec{v}_{D1} \vert _2 = \sqrt{1.0^2 + 1.0^2 + 1.0^2} = \sqrt{1 + 1 + 1} = \sqrt{3}\]Agora, dividimos cada componente do vetor original pela norma $\sqrt{3}$:
\[\vec{v}_{D1}^{\text{norm}} = \left[ \frac{1.0}{\sqrt{3}}, \frac{1.0}{\sqrt{3}}, \frac{1.0}{\sqrt{3}} \right]\]Este vetor $\vec{v}_{D1}^{\text{norm}}$ é a representação final (normalizada) do Documento 1 no espaço vetorial definido pelas 3 transições mais frequentes do corpus.
4. Comparação entre Documentos
Com os documentos representados como vetores probabilísticos normalizados, podemos calcular a similaridade entre eles usando medidas como:
-
Similaridade de cosseno:
\[sim(d_1, d_2) = \frac{\vec{v}_{d_1} \cdot \vec{v}_{d_2}}{\vert \vec{v}_{d_1}\vert \cdot \vert \vec{v}_{d_2} \vert }\] -
Distância euclidiana:
\[dist(d_1, d_2) = \vert \vec{v}_{d_1} - \vec{v}_{d_2} \vert\] -
Divergência KL: para comparar distribuições de probabilidade diretamente.
\[D_{KL}(P || Q) = \sum_{i} P(i) \log\left(\frac{P(i)}{Q(i)}\right)\]
Divergência Kullback-Leibler (KL)
A Divergência KL é uma medida estatística que quantifica a diferença entre duas distribuições de probabilidade. Originalmente desenvolvida por Solomon Kullback e Richard Leibler em 1951, esta métrica tem aplicações importantes em teoria da informação, aprendizado de máquina e processamento de linguagem natural.
Matematicamente, para distribuições discretas, a Divergência KL de Q para P é definida como:
\[D_{KL}(P || Q) = \sum_{i} P(i) \log\left(\frac{P(i)}{Q(i)}\right)\]Na qual, temos:
- $P$ é a distribuição de interesse (ex: distribuição de probabilidades de transição em um documento específico)
- $Q$ é a distribuição de referência (ex: modelo agregado do corpus)
- A soma é realizada sobre todos os estados possíveis (todas as transições possíveis)
Interpretação intuitiva: A Divergência KL mede a informação perdida quando usamos a distribuição $Q$ para aproximar a distribuição $P$. Pode ser entendida como o “custo” (em bits, quando se usa logaritmo de base 2) de usar $Q$ em vez de $P$.
Propriedades importantes:
- $D_{KL}(P \vert \vert Q) \geq 0$ para quaisquer distribuições $P$ e $Q$
- $D_{KL}(P \vert \vert Q) = 0$ se e somente se $P = Q$ (as distribuições são idênticas)
- $D_{KL}(P \vert \vert Q) \neq D_{KL}(Q \vert \vert P)$ (não é simétrica, portanto não é uma métrica de distância)
No contexto de modelagem de sequências:
- Podemos usar a Divergência KL para comparar as distribuições de probabilidades de transição entre um documento específico ($P_D$) e o modelo agregado do corpus ($P_{corpus}\;$)
- Um valor alto de $D_{KL}(P_D \vert \vert P_{corpus}\;)$ indica que o documento tem um padrão de transições muito diferente da média do corpus
- Esta medida pode revelar características distintivas de documentos que não são capturadas por outras métricas de similaridade
Implementação em C++
Vejamos como implementar esta abordagem em C++:
#include <iostream> ///< Para entrada e saída padrão (std::cout, std::cerr).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de corpus, vocabulário e vetores.
#include <string> ///< Para std::string, usado em palavras e mensagens.
#include <unordered_map> ///< Para std::unordered_map, usado no mapeamento de palavras para índices.
#include <map> ///< Para std::map, usado na contagem ordenada de bigramas.
#include <Eigen/Dense> ///< Para a biblioteca Eigen, usada em operações com matrizes e vetores.
#include <cmath> ///< Para std::log e std::sqrt, usados em cálculos matemáticos.
#include <iomanip> ///< Para std::fixed, std::setprecision e std::setw, usados na formatação de saída.
#include <algorithm> ///< Para std::sort, usado na ordenação de listas e vocabulário.
/**
* @struct BigramInfo
* @brief Estrutura para armazenar informações sobre um bigrama, incluindo índices, palavras e frequência.
*/
struct BigramInfo {
std::pair<int, int> indices; ///< Índices do bigrama (primeira e segunda palavra).
std::string firstWord; ///< Primeira palavra do bigrama.
std::string secondWord; ///< Segunda palavra do bigrama.
int frequency = 0; ///< Frequência do bigrama no corpus.
/**
* @brief Operador de comparação para ordenação por frequência decrescente.
* @param other Outro objeto BigramInfo a ser comparado.
* @return true se a frequência atual for maior que a do outro.
*/
bool operator<(const BigramInfo& other) const {
return frequency > other.frequency;
}
};
/**
* @class ProbabilisticNGramVectorizer
* @brief Uma classe para vetorizar documentos com base em probabilidades de transição de bigramas.
*
* Esta classe constrói um vocabulário, calcula matrizes de transição de bigramas para documentos,
* vetoriza documentos usando métodos completo e específico, normaliza vetores de características,
* e calcula similaridades de cosseno entre documentos. Utiliza a biblioteca Eigen para operações matriciais.
*/
class ProbabilisticNGramVectorizer {
private:
std::vector<std::string> vocabulary; ///< Vocabulário global ordenado alfabeticamente.
std::unordered_map<std::string, int> wordToIndex; ///< Mapeamento de palavras para índices no vocabulário.
int vocabSize; ///< Tamanho do vocabulário.
/**
* @brief Extrai índices de bigramas de um documento tokenizado.
* @param tokens Vetor de strings representando o documento tokenizado.
* @return Vetor de pares de índices correspondentes aos bigramas encontrados.
*/
std::vector<std::pair<int, int>> extractBigramIndices(const std::vector<std::string>& tokens) {
std::vector<std::pair<int, int>> bigramIndices;
for (size_t i = 0; i < tokens.size() - 1; ++i) {
if (wordToIndex.count(tokens[i]) && wordToIndex.count(tokens[i+1])) {
int firstIdx = wordToIndex.at(tokens[i]);
int secondIdx = wordToIndex.at(tokens[i+1]);
bigramIndices.push_back({firstIdx, secondIdx});
}
}
return bigramIndices;
}
public:
/**
* @brief Construtor que inicializa o vetorizador com um vocabulário.
* @param vocab Vetor de strings contendo as palavras do vocabulário.
*/
ProbabilisticNGramVectorizer(const std::vector<std::string>& vocab) : vocabulary(vocab), vocabSize(vocab.size()) {
for (int i = 0; i < vocabSize; ++i) {
wordToIndex[vocabulary[i]] = i;
}
}
/**
* @brief Cria a matriz de transição de bigramas para um documento.
* @param documentTokens Vetor de strings representando o documento tokenizado.
* @return Matriz de transição (Eigen::MatrixXd) com probabilidades P(w_j | w_i, D).
*/
Eigen::MatrixXd createTransitionMatrix(const std::vector<std::string>& documentTokens) {
Eigen::MatrixXd transMatrix = Eigen::MatrixXd::Zero(vocabSize, vocabSize);
Eigen::VectorXd firstWordCounts = Eigen::VectorXd::Zero(vocabSize);
std::vector<std::pair<int, int>> bigramIndices = extractBigramIndices(documentTokens);
for (const auto& bigram : bigramIndices) {
transMatrix(bigram.first, bigram.second) += 1.0;
firstWordCounts(bigram.first) += 1.0;
}
for (int i = 0; i < vocabSize; ++i) {
double count_wi = firstWordCounts(i);
if (count_wi > 0) {
for (int j = 0; j < vocabSize; ++j) {
transMatrix(i, j) /= count_wi;
}
}
}
return transMatrix;
}
/**
* @brief Vetoriza a matriz de transição usando o método completo.
* @param transMatrix Matriz de transição do documento.
* @return Vetor de características (std::vector<double>) no formato [i, j, p, ...].
*/
std::vector<double> vectorizeFull(const Eigen::MatrixXd& transMatrix) {
std::vector<double> featureVector;
featureVector.reserve(transMatrix.nonZeros() * 3);
for (int i = 0; i < vocabSize; ++i) {
for (int j = 0; j < vocabSize; ++j) {
if (transMatrix(i, j) > 1e-9) {
featureVector.push_back(static_cast<double>(i));
featureVector.push_back(static_cast<double>(j));
featureVector.push_back(transMatrix(i, j));
}
}
}
return featureVector;
}
/**
* @brief Vetoriza a matriz de transição usando transições específicas.
* @param transMatrix Matriz de transição do documento.
* @param selectedTransitions Vetor de pares de índices representando as transições selecionadas.
* @return Vetor de características (Eigen::VectorXd) com probabilidades das transições selecionadas.
*/
Eigen::VectorXd vectorizeSpecific(const Eigen::MatrixXd& transMatrix,
const std::vector<std::pair<int, int>>& selectedTransitions) {
int k = selectedTransitions.size();
Eigen::VectorXd featureVector = Eigen::VectorXd::Zero(k);
for (int feature_idx = 0; feature_idx < k; ++feature_idx) {
int i = selectedTransitions[feature_idx].first;
int j = selectedTransitions[feature_idx].second;
if (i >= 0 && i < vocabSize && j >= 0 && j < vocabSize) {
featureVector(feature_idx) = transMatrix(i, j);
}
}
return featureVector;
}
/**
* @brief Normaliza um vetor de características usando a norma L2.
* @param featureVector Vetor de características (Eigen::VectorXd) a ser normalizado.
* @return Vetor normalizado (Eigen::VectorXd). Retorna o vetor original se a norma for zero.
*/
Eigen::VectorXd normalizeFeatureVector(Eigen::VectorXd featureVector) {
double norm = featureVector.norm();
if (norm > 1e-9) {
featureVector /= norm;
}
return featureVector;
}
/**
* @brief Calcula a similaridade de cosseno entre dois vetores normalizados.
* @param normalized_v1 Primeiro vetor normalizado (Eigen::VectorXd).
* @param normalized_v2 Segundo vetor normalizado (Eigen::VectorXd).
* @return Valor da similaridade de cosseno (double). Retorna 0.0 para vetores incompatíveis ou nulos.
*/
double cosineSimilarity(const Eigen::VectorXd& normalized_v1, const Eigen::VectorXd& normalized_v2) {
if (normalized_v1.size() != normalized_v2.size() || normalized_v1.size() == 0) {
return 0.0;
}
return normalized_v1.dot(normalized_v2);
}
/**
* @brief Obtém o vocabulário global.
* @return Referência constante ao vetor de strings do vocabulário.
*/
const std::vector<std::string>& getVocabulary() const {
return vocabulary;
}
/**
* @brief Obtém o tamanho do vocabulário.
* @return O número de termos no vocabulário (int).
*/
int getVocabSize() const {
return vocabSize;
}
/**
* @brief Mapeia uma palavra para seu índice no vocabulário.
* @param word A palavra a ser mapeada.
* @return O índice da palavra no vocabulário, ou -1 se não encontrada.
*/
int getIndexForWord(const std::string& word) const {
auto it = wordToIndex.find(word);
return it != wordToIndex.end() ? it->second : -1;
}
/**
* @brief Mapeia um índice para a palavra correspondente no vocabulário.
* @param index O índice a ser mapeado.
* @return A palavra correspondente, ou "[INVALID_INDEX]" se o índice for inválido.
*/
std::string getWordForIndex(int index) const {
if (index >= 0 && index < vocabSize) {
return vocabulary[index];
}
return "[INVALID_INDEX]";
}
/**
* @brief Analisa a frequência de bigramas em um corpus.
* @param corpusTokens Vetor de vetores de strings representando o corpus tokenizado.
* @param vocab Vetor de strings contendo o vocabulário.
* @param wordToIdx Mapeamento de palavras para índices.
* @return Vetor de objetos BigramInfo ordenado por frequência decrescente.
*/
static std::vector<BigramInfo> analyzeCorpusBigramFrequency(
const std::vector<std::vector<std::string>>& corpusTokens,
const std::vector<std::string>& vocab,
const std::unordered_map<std::string, int>& wordToIdx) {
std::map<std::pair<int, int>, int> bigramCounts;
for (const auto& docTokens : corpusTokens) {
for (size_t i = 0; i < docTokens.size() - 1; ++i) {
if (wordToIdx.count(docTokens[i]) && wordToIdx.count(docTokens[i+1])) {
int idx1 = wordToIdx.at(docTokens[i]);
int idx2 = wordToIdx.at(docTokens[i+1]);
bigramCounts[{idx1, idx2}]++;
}
}
}
std::vector<BigramInfo> frequencyList;
for (const auto& pair : bigramCounts) {
BigramInfo info;
info.indices = pair.first;
info.frequency = pair.second;
if (pair.first.first >= 0 && pair.first.first < vocab.size()) {
info.firstWord = vocab[pair.first.first];
}
if (pair.first.second >= 0 && pair.first.second < vocab.size()) {
info.secondWord = vocab[pair.first.second];
}
frequencyList.push_back(info);
}
std::sort(frequencyList.begin(), frequencyList.end());
return frequencyList;
}
};
/**
* @brief Função principal que demonstra o uso da classe ProbabilisticNGramVectorizer.
*
* Este programa cria um vetorizador de bigramas com um vocabulário predefinido, analisa a frequência
* de bigramas em um corpus, vetoriza documentos usando métodos completo e específico, normaliza vetores
* de características, e calcula similaridades de cosseno entre documentos.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
std::cout << std::fixed << std::setprecision(3); ///< Define precisão de saída para três casas decimais.
// Definir o vocabulário
std::vector<std::string> vocabulary = {
"mostre", "me", "meus", "diretórios", "por", "favor", "arquivos", "minhas", "fotos"
};
// Corpus de documentos tokenizados
std::vector<std::vector<std::string>> corpusDocs = {
{"mostre", "me", "meus", "diretórios", "por", "favor"}, // Doc 1
{"mostre", "me", "meus", "arquivos", "por", "favor"}, // Doc 2
{"mostre", "me", "minhas", "fotos", "por", "favor"} // Doc 3
};
// Criar o vetorizador
ProbabilisticNGramVectorizer vectorizer(vocabulary); ///< Instância do vetorizador.
int vocabSize = vectorizer.getVocabSize();
std::cout << ">>> ANÁLISE DO CORPUS E VETORIZAÇÃO <<<\n\n";
// Analisar frequência de bigramas no corpus
std::cout << "--- Análise de Frequência de Bigramas no Corpus ---\n";
auto corpusBigramFrequencies = ProbabilisticNGramVectorizer::analyzeCorpusBigramFrequency(
corpusDocs, vectorizer.getVocabulary(), vectorizer.wordToIndex);
std::cout << "Frequências encontradas (Top 5 ou todas se menos de 5):\n";
int count = 0;
for (const auto& info : corpusBigramFrequencies) {
std::cout << " (" << info.firstWord << ", " << info.secondWord << "): " << info.frequency << "\n";
if (++count >= 5) break;
}
// Selecionar as top K transições
int K = 3;
std::vector<std::pair<int, int>> selectedTransitionsIndices;
if (corpusBigramFrequencies.size() >= K) {
std::cout << "\nSelecionando as Top " << K << " transições mais frequentes:\n";
for (int i = 0; i < K; ++i) {
selectedTransitionsIndices.push_back(corpusBigramFrequencies[i].indices);
std::cout << " Selecionada: (" << corpusBigramFrequencies[i].firstWord << ", "
<< corpusBigramFrequencies[i].secondWord << ")\n";
}
} else {
std::cout << "\nNão há " << K << " bigramas únicos, usando todos os " << corpusBigramFrequencies.size() << " encontrados.\n";
for (const auto& info : corpusBigramFrequencies) {
selectedTransitionsIndices.push_back(info.indices);
}
K = selectedTransitionsIndices.size();
}
std::cout << "\n";
// Processar cada documento
std::vector<Eigen::VectorXd> normalizedVectorsMethod2;
for (size_t doc_idx = 0; doc_idx < corpusDocs.size(); ++doc_idx) {
const auto& currentDocTokens = corpusDocs[doc_idx];
std::cout << "--- Processando Documento " << (doc_idx + 1) << " ---\n";
// Etapa 1: Criar matriz de transição
Eigen::MatrixXd tMatrix = vectorizer.createTransitionMatrix(currentDocTokens);
std::cout << "Etapa 1: Matriz de Transição T_D (mostrando apenas transições não-zero):\n";
bool found_transition = false;
for (int i = 0; i < vocabSize; ++i) {
for (int j = 0; j < vocabSize; ++j) {
if (tMatrix(i, j) > 1e-9) {
std::cout << " P(" << vectorizer.getWordForIndex(j) << " | " << vectorizer.getWordForIndex(i) << ") = " << tMatrix(i, j) << "\n";
found_transition = true;
}
}
}
if (!found_transition) std::cout << " (Nenhuma transição encontrada neste documento)\n";
// Etapa 2, Método 1: Vetorização completa
std::vector<double> fullVector = vectorizer.vectorizeFull(tMatrix);
std::cout << "Etapa 2, Método 1 (Vetorização Completa): [i, j, p, ...]\n [";
for (size_t k = 0; k < fullVector.size(); ++k) {
std::cout << fullVector[k] << ((k == fullVector.size()-1) ? "" : ((k+1)%3 == 0 ? "; " : ", "));
}
std::cout << "]\n";
// Etapa 2, Método 2: Vetorização por transições específicas
Eigen::VectorXd specificVector_unnormalized = vectorizer.vectorizeSpecific(tMatrix, selectedTransitionsIndices);
std::cout << "Etapa 2, Método 2 (Vetorização por Transições Específicas - Top " << K << "):\n [";
for (int k = 0; k < specificVector_unnormalized.size(); ++k) {
std::cout << specificVector_unnormalized(k) << (k == specificVector_unnormalized.size() - 1 ? "" : ", ");
}
std::cout << "] (Antes da Normalização)\n";
// Etapa 3: Normalização do vetor (Método 2)
Eigen::VectorXd specificVector_normalized = vectorizer.normalizeFeatureVector(specificVector_unnormalized);
std::cout << "Etapa 3: Normalização (L2) do Vetor do Método 2:\n [";
for (int k = 0; k < specificVector_normalized.size(); ++k) {
std::cout << specificVector_normalized(k) << (k == specificVector_normalized.size() - 1 ? "" : ", ");
}
std::cout << "]\n";
normalizedVectorsMethod2.push_back(specificVector_normalized);
std::cout << "\n";
}
// Etapa 4: Comparação entre documentos
std::cout << "--- Etapa 4: Comparação entre Documentos (Similaridade de Cosseno usando Método 2) ---\n";
if (normalizedVectorsMethod2.size() >= 2) {
for (size_t i = 0; i < normalizedVectorsMethod2.size(); ++i) {
for (size_t j = i + 1; j < normalizedVectorsMethod2.size(); ++j) {
double sim = vectorizer.cosineSimilarity(normalizedVectorsMethod2[i], normalizedVectorsMethod2[j]);
std::cout << " Similaridade entre Doc " << (i + 1) << " e Doc " << (j + 1)
<< ": " << sim << "\n";
}
}
} else {
std::cout << " São necessários pelo menos 2 documentos para comparação.\n";
}
return 0;
}
Neste código, a classe ProbabilisticNGramVectorizer encapsula a lógica para construir matrizes de transição (Etapa 1), gerar vetores de características através de diferentes métodos de compactação (Etapa 2) e normalizá-los (Etapa 3), além de calcular similaridades (Etapa 4). O exemplo em main utiliza um corpus de três documentos. A saída do programa demonstra cada etapa: exibe as probabilidades da matriz de transição, os vetores resultantes de ambos os métodos de vetorização, Completa e por Transições Específicas, incluindo a versão normalizada deste último. E, finalmente, calcula e mostra as similaridades de cosseno entre os documentos usando os vetores normalizados derivados do método de Transições Específicas.
Exemplo Estendido - Mais próximo do Mundo Real
A ávida leitora deve se preparar para emoções fortes. Vamos explorar uma aplicação um pouco mais elaborada da Vetorização Probabilística N-gram, utilizando um corpus mais variado e incorporando uma técnica extra: um token especial para marcar o início dos documentos.
Até agora, tratamos todas as palavras de forma semelhante. No entanto, a primeira palavra de um documento pode carregar informações importantes sobre seu tipo, intenção ou estilo. Para capturar explicitamente essa informação inicial, podemos introduzir um token especial, como <START>, no início de cada sequência de palavras do documento antes de aplicar nosso processo de vetorização. Este token precisa ser criado de forma a ser único e não aparecer em nenhum outro lugar do corpus.
Este token <START> irá permitir avaliar as características das palavras que iniciam cada documento do corpus. Estas palavras podem seguir distribuições diferentes das palavras no meio do texto. Modelar a transição a partir de <START> ajuda a capturar essas tendências (ex: comandos frequentemente começam com verbos, perguntas com pronomes interrogativos, etc.).
Para entender o efeito das palavras iniciais, vamos considerar um corpus de exemplo com $8$ documentos:
- $D_1$:
Mostre-me meus documentos importantes. - $D_2$:
Mostre-me meus arquivos recentes, por favor. - $D_3$:
Por favor mostre meus documentos financeiros. - $D_4$:
Mostre-me minhas fotos favoritas urgentemente. - $D_5$:
Preciso ver meus documentos de trabalho. - $D_6$:
Mostre meus arquivos de projeto imediatamente. - $D_7$:
Por favor encontre meus documentos fiscais. - $D_8$:
Gostaria de ver meus arquivos pessoais agora.
Vamos passar este corpus pelo mesmo pré-processamento básico anterior (minúsculas, remover pontuação), e incluir <START>:
- $D_1$:
[<START>, mostre, me, meus, documentos, importantes] - $D_2$:
[<START>, mostre, me, meus, arquivos, recentes, por, favor] - $D_3$:
[<START>, por, favor, mostre, meus, documentos, financeiros] - $D_4$:
[<START>, mostre, me, minhas, fotos, favoritas, urgentemente] - $D_5$:
[<START>, preciso, ver, meus, documentos, de, trabalho] - $D_6$:
[<START>, mostre, meus, arquivos, de, projeto, imediatamente] - $D_7$:
[<START>, por, favor, encontre, meus, documentos, fiscais] - $D_8$:
[<START>, gostaria, de, ver, meus, arquivos, pessoais, agora]
Feito isso, teremos o seguinte vocabulário:
\[V = \left\{ \begin{array}{l} \text{<START>}, \text{mostre}, \text{me}, \text{meus}, \text{documentos}, \text{importantes}, \\ \text{arquivos}, \text{recentes}, \text{por}, \text{favor}, \text{financeiros}, \text{minhas}, \\ \text{fotos}, \text{favoritas}, \text{urgentemente}, \text{preciso}, \text{ver}, \text{de}, \\ \text{trabalho}, \text{projeto}, \text{imediatamente}, \text{encontre}, \text{fiscais}, \\ \text{gostaria}, \text{pessoais}, \text{agora} \end{array} \right\}\]Logo:
\[\vert V \vert = 26\]Vamos seguir as 4 etapas definidas anteriormente para o Documento $D_1$: [<START>, mostre, me, meus, documentos, importantes]
Etapa 1: Construção da Matriz de Transição $T_{D1}$
Calculamos $T_{D1}(i, j) = P(w_j \vert w_i, D1) = \frac{\text{count}(w_i, w_j, D1)}{\text{count}(w_i, D1)}$ para $D_1$. Neste documento específico, cada palavra é seguida por exatamente uma outra palavra única. As transições não-zero serão:
- $P(\text{mostre} \vert \text{
}, D1) = 1/1 = 1.0$; - $P(\text{me} \vert \text{mostre}, D1) = 1/1 = 1.0$;
- $P(\text{meus} \vert \text{me}, D1) = 1/1 = 1.0$;
- $P(\text{documentos} \vert \text{meus}, D1) = 1/1 = 1.0$;
- $P(\text{importantes} \vert \text{documentos}, D1) = 1/1 = 1.0$.
Todas as outras entradas na matriz $T_{D1}$ (de tamanho $26 \times 26$) são $0$.
Etapa 2: Compactação da Matriz $T_{D1}$ em Vetor
Aplicamos os dois métodos de compactação que definimos anteriormente:
-
Vetorização Completa: quando mapeamos as palavras para índices do vocabulário $V$ (ex:
\[\vec{v}_{D1} = [0, 1, 1.0, \quad 1, 2, 1.0, \quad 2, 3, 1.0, \quad 3, 4, 1.0, \quad 4, 5, 1.0]\]<START>=0, mostre=1, me=2, meus=3, documentos=4, importantes=5, …), o vetor $\vec{v}_{D1}$ será dado por:Este vetor contém $5$ transições, então tem $5 \times 3 = 15$ elementos.
-
Vetorização por Transições Específicas: vamos escolher as transições mais frequentes do corpus para representar o documento. Para isso, seguiremos os seguintes passos:
-
Análise de Frequência no Corpus: Primeiro, precisamos analisar todo o corpus (com
<START>) para encontrar as transições mais frequentes.- Contagem de Bigramas:
- (
, mostre): 4; - (
, por): 2; - (
, preciso): 1; - (
, gostaria): 1; - (mostre, me): 3;
- (mostre, meus): 1 (em D6);
- (me, meus): 2;
- (meus, documentos): 4 (em D1, D3, D5, D7);
- (meus, arquivos): 3 (em D2, D6, D8);
- (por, favor): 2;
- (documentos, importantes): 1;
- (documentos, financeiros): 1;
- (documentos, de): 1;
- (documentos, fiscais): 1;
- … (e outras transições com frequência 1 ou mais).
- (
- Contagem de Bigramas:
-
Seleção das Top K Transições: Vamos selecionar as $K=5$ transições mais frequentes no corpus (incluindo empates se houver):
- $t_1 = (\text{
}, \text{mostre})$ (Freq: 4); - $t_2 = (\text{meus}, \text{documentos})$ (Freq: 4);
- $t_3 = (\text{mostre}, \text{me})$ (Freq: 3);
- $t_4 = (\text{meus}, \text{arquivos})$ (Freq: 3);
- $t_5 = (\text{por}, \text{favor})$ (Freq: 2).
- $t_1 = (\text{
-
Criação do Vetor $\vec{v}_{D1}$: Construímos o vetor buscando as probabilidades $P(t_m \vert D1)$ para estas $$5$ transições no Documento 1:
- $P(t_1 \vert D1) = P(\text{mostre} \vert \text{
}, D1) = 1.0$; - $P(t_2 \vert D1) = P(\text{documentos} \vert \text{meus}, D1) = 1.0$;
- $P(t_3 \vert D1) = P(\text{me} \vert \text{mostre}, D1) = 1.0$;
- $P(t_4 \vert D1) = P(\text{arquivos} \vert \text{meus}, D1) = 0.0$ (transição ‘meus -> arquivos’ não ocorre em D1);
- $P(t_5 \vert D1) = P(\text{favor} \vert \text{por}, D1) = 0.0$ (transição ‘por -> favor’ não ocorre em D1).
- $P(t_1 \vert D1) = P(\text{mostre} \vert \text{
O vetor resultante (antes da normalização) para $D_1$ usando este método é:
\[\vec{v}_{D1} = [1.0, 1.0, 1.0, 0.0, 0.0]\] -
Etapa 3: Normalização do Vetor de Características
Aplicamos a normalização L2 ao vetor $\vec{v}_{D1}$ obtido pelo Método 2:
\[\vert \vec{v}_{D1} \vert _2 = \sqrt{1.0^2 + 1.0^2 + 1.0^2 + 0.0^2 + 0.0^2} = \sqrt{3}\] \[\vec{v}_{D1}^{\text{norm}} = \left[ \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, 0.0, 0.0 \right] \approx [0.577, 0.577, 0.577, 0.0, 0.0]\]Este é o vetor final que representa $D_1$ neste espaço de características.
Etapa 4: Comparação entre Documentos
Com os vetores normalizados para todos os documentos (calculados da mesma forma usando as mesmas $5$ transições selecionadas), podemos calcular a similaridade de cosseno ou outras métricas entre eles. Por exemplo, poderíamos calcular $\text{sim}(D_1, D_3)$ usando $\vec{v_{D1}^{\text{norm}}}$ e $\vec{v_{D3}^{\text{norm}}}$.
Modelo de Linguagem Agregado do Corpus ($P_{corpus}\;$)
O modelo de linguagem agregado do corpus representa as tendências médias de sequenciamento de palavras em todo o corpus. Este modelo, que denominamos $P_{corpus}\;$, funciona como uma linha de base (baseline) do uso da linguagem específico para o conjunto de documentos analisado.
Diferentemente das probabilidades específicas por documento $P_D(w_j \vert w_i)$ que refletem os padrões de um único documento $D$, o modelo agregado $P_{corpus}\;$ captura os padrões gerais de toda a coleção.
Para calcular $P_{corpus}\;(w_j \vert w_i)$, precisamos considerar todas as ocorrências de $w_i$ e $w_j$ em todos os documentos do corpus. Isso nos dá uma visão mais ampla de como as palavras se relacionam entre si em um contexto mais amplo.
\[P_{corpus}\;(w_j \vert w_i) = \frac{\sum_{D \in \text{Corpus}} \text{count}(w_i, w_j, D)}{\sum_{D \in \text{Corpus}} \text{count}(w_i, D)}\]Na qual, teremos:
- $\sum_{D \in \text{Corpus}} \text{count}(w_i, w_j, D)$ é a soma de todas as ocorrências do bigrama $(w_i, w_j)$ em todos os documentos
- $\sum_{D \in \text{Corpus}} \text{count}(w_i, D)$ é a soma de todas as ocorrências da palavra $w_i$ como primeira palavra de um par
A esforçada leitora deve se lembrar que o corpus é composto por $8$ documentos, e que a contagem de palavras é feita considerando todas as ocorrências em todos os documentos. Recordando o corpus que estamos utilizando:
- $D_1$:
[<START>, mostre, me, meus, documentos, importantes] - $D_2$:
[<START>, mostre, me, meus, arquivos, recentes, por, favor] - $D_3$:
[<START>, por, favor, mostre, meus, documentos, financeiros] - $D_4$:
[<START>, mostre, me, minhas, fotos, favoritas, urgentemente] - $D_5$:
[<START>, preciso, ver, meus, documentos, de, trabalho] - $D_6$:
[<START>, mostre, meus, arquivos, de, projeto, imediatamente] - $D_7$:
[<START>, por, favor, encontre, meus, documentos, fiscais] - $D_8$:
[<START>, gostaria, de, ver, meus, arquivos, pessoais, agora]
Com vocabulário $\vert V \vert$ de $26$ palavras:
\[V = \left\{ \begin{array}{l} \text{<START>}, \text{mostre}, \text{me}, \text{meus}, \text{documentos}, \text{importantes}, \\ \text{arquivos}, \text{recentes}, \text{por}, \text{favor}, \text{financeiros}, \text{minhas}, \\ \text{fotos}, \text{favoritas}, \text{urgentemente}, \text{preciso}, \text{ver}, \text{de}, \\ \text{trabalho}, \text{projeto}, \text{imediatamente}, \text{encontre}, \text{fiscais}, \\ \text{gostaria}, \text{pessoais}, \text{agora} \end{array} \right\}\]A seguir, calculamos explicitamente algumas probabilidades importantes $P_{corpus}\;(w_j \vert w_i)$:
-
$P_{corpus}\;(\text{mostre} \vert \text{<}\text{START}\text{>})$:
- Numerador: Contagem de (
<START>,mostre) = 4 (ocorre em D1, D2, D4, D6) - Denominador: Contagem de
<START>= 8 (ocorre em todos os documentos) - Probabilidade: $\frac{4}{8} = 0.50$
- Numerador: Contagem de (
-
**$P_{corpus}\;(\text{por} \vert \text{
})$**: - Numerador: Contagem de (
<START>,por) = 2 (ocorre em D3, D7) - Denominador: Contagem de
<START>= 8 - Probabilidade: $\frac{2}{8} = 0.25$
- Numerador: Contagem de (
-
**$P_{corpus}\;(\text{preciso} \vert \text{
})$**: - Numerador: Contagem de (
<START>,preciso) = 1 (ocorre em D5) - Denominador: Contagem de
<START>= 8 - Probabilidade: $\frac{1}{8} = 0.125$
- Numerador: Contagem de (
-
**$P_{corpus}\;(\text{gostaria} \vert \text{
})$**: - Numerador: Contagem de (
<START>,gostaria) = 1 (ocorre em D8) - Denominador: Contagem de
<START>= 8 - Probabilidade: $\frac{1}{8} = 0.125$
- Numerador: Contagem de (
-
$P_{corpus}\;(\text{documentos} \vert \text{meus})$:
- Numerador: Contagem de (
meus,documentos) = 4 (ocorre em D1, D3, D5, D7) - Denominador: Contagem de
meus= 7 (ocorre em D1, D2, D3, D5, D6, D7, D8) - Probabilidade: $\frac{4}{7} \approx 0.571$
- Numerador: Contagem de (
-
$P_{corpus}\;(\text{arquivos} \vert \text{meus})$:
- Numerador: Contagem de (
meus,arquivos) = 3 (ocorre em D2, D6, D8) - Denominador: Contagem de
meus= 7 - Probabilidade: $\frac{3}{7} \approx 0.429$
- Numerador: Contagem de (
-
$P_{corpus}\;(\text{me} \vert \text{mostre})$:
- Numerador: Contagem de (
mostre,me) = 3 (ocorre em D1, D2, D4) - Denominador: Contagem de
mostre= 5 (ocorre em D1, D2, D3, D4, D6) - Probabilidade: $\frac{3}{5} = 0.60$
- Numerador: Contagem de (
-
$P_{corpus}\;(\text{meus} \vert \text{mostre})$:
- Numerador: Contagem de (
mostre,meus) = 2 (ocorre em D3, D6) - Denominador: Contagem de
mostre= 5 - Probabilidade: $\frac{2}{5} = 0.40$
- Numerador: Contagem de (
-
$P_{corpus}\;(\text{favor} \vert \text{por})$:
- Numerador: Contagem de (
por,favor) = 3 (ocorre em D2, D3, D7) - Denominador: Contagem de
por= 3 - Probabilidade: $\frac{3}{3} = 1.0$
- Numerador: Contagem de (
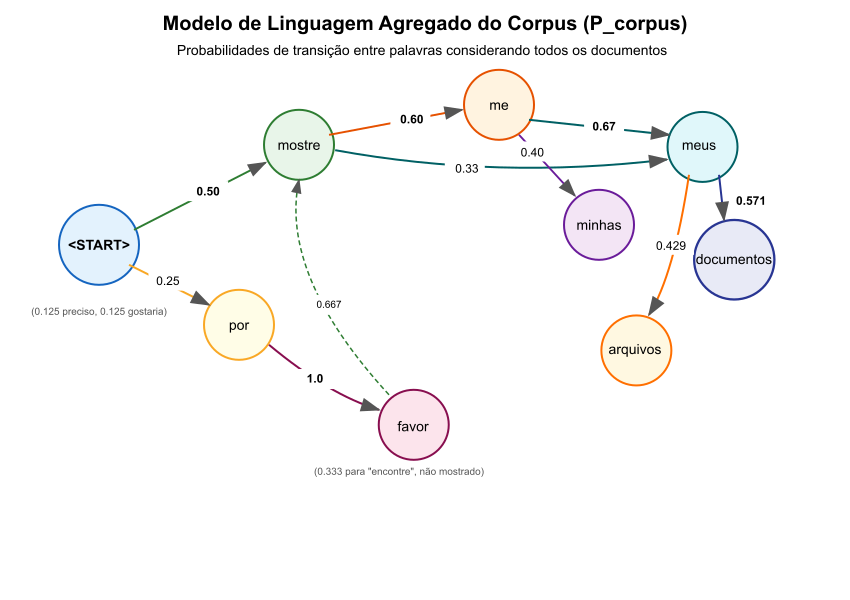 Figura 3: Grafo direcionado com as probabilidades do modelo de linguagem agregado, ilustrando como as palavras do vocabulário se conectam com diferentes probabilidades.
Figura 3: Grafo direcionado com as probabilidades do modelo de linguagem agregado, ilustrando como as palavras do vocabulário se conectam com diferentes probabilidades.
A matriz de transição $T_{corpus}\;$ representando $P_{corpus}\;$ seria uma matriz $26 \times 26$ (tamanho do vocabulário). Como esta matriz é esparsa, vamos mostrar apenas as entradas não-zero mais relevantes:
| $w_i$ \ $w_j$ | mostre | me | meus | minhas | documentos | arquivos | por | favor | ver | encontre | … |
|---|---|---|---|---|---|---|---|---|---|---|---|
| <START> | 0.50 | 0 | 0 | 0 | 0 | 0 | 0.25 | 0 | 0 | 0 | … |
| mostre | 0 | 0.60 | 0.40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| me | 0 | 0 | 0.67 | 0.33 | 0 | 0 | 0 | 0 | 0 | 0 | … |
| meus | 0 | 0 | 0 | 0 | 0.571 | 0.429 | 0 | 0 | 0 | 0 | … |
| por | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.0 | 0 | 0 | … |
| favor | 0.667 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.333 | … |
| … | … | … | … | … | … | … | … | … | … | … | … |
Usando o Modelo Agregado
Agora vamos ilustrar como usar o modelo $P_{corpus}\;$ para construir diferentes tipos de vetores para os documentos:
-
Vetorização por Transições Específicas ($K=5$): recordando nossas $5$ transições mais frequentes:
- $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$ (Freq: 4);
- $t_2 = (\text{meus}, \text{documentos})$ (Freq: 4);
- $t_3 = (\text{mostre}, \text{me})$ (Freq: 3);
- $t_4 = (\text{meus}, \text{arquivos})$ (Freq: 3);
- $t_5 = (\text{por}, \text{favor})$ (Freq: 3).
Para cada transição $t_i$, $P_{corpus}\;(t_i)$ é:
- $P_{corpus}\;(t_1) = P_{corpus}\;(\text{mostre} \vert \text{
}) = 0.50$ - $P_{corpus}\;(t_2) = P_{corpus}\;(\text{documentos} \vert \text{meus}) = 0.571$
- $P_{corpus}\;(t_3) = P_{corpus}\;(\text{me} \vert \text{mostre}) = 0.60$
- $P_{corpus}\;(t_4) = P_{corpus}\;(\text{arquivos} \vert \text{meus}) = 0.429$
- $P_{corpus}\;(t_5) = P_{corpus}\;(\text{favor} \vert \text{por}) = 1.0$
Vamos então construir vetores para cada documento usando estas probabilidades do modelo agregado:
-
Vetorização por Razão de Verossimilhança: a vetorização por razão de verossimilhança compara as probabilidades específicas do documento com as do Modelo de Linguagem Agregado do Corpus:
\[\vec{v}_D^{*} = \left[ \frac{P_D(t_1)}{P_{corpus}\;(t_1)}, \frac{P_D(t_2)}{P_{corpus}\;(t_2)}, ..., \frac{P_D(t_k)}{P_{corpus}\;(t_k)} \right]\]Vamos calcular os vetores completos para os primeiros três documentos:
-
Documento $D_1$:
[<START>, mostre, me, meus, documentos, importantes]Transição $P_{D1}(t_i)$ $P_{corpus}\;(t_i)$ Razão $\frac{P_{D1}(t_i)}{P_{corpus}\;(t_i)}$ $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$ 1.0 0.50 2.0 $t_2 = (\text{meus}, \text{documentos})$ 1.0 0.571 1.75 $t_3 = (\text{mostre}, \text{me})$ 1.0 0.60 1.67 $t_4 = (\text{meus}, \text{arquivos})$ 0.0 0.429 0.0 $t_5 = (\text{por}, \text{favor})$ 0.0* 1.0 0.0 Em $D_1$, “por” não aparece, então $P_{D1}(\text{favor} \vert \text{por})$ é indefinido. Atribuímos $0.0$ pois a transição não ocorre.
Vetor $D_1$ não normalizado: $\vec{v_{D1}^{*}} = [2.0, 1.75, 1.67, 0.0, 0.0]$
Vetor $D_1$ normalizado (L2):
\[\vert \vec{v_{D1}^{*}} \vert _2 = \sqrt{2.0^2 + 1.75^2 + 1.67^2 + 0.0^2 + 0.0^2} = \sqrt{10.1989} \approx 3.193\] \[\vec{v}_{D1}^{*norm} = [\frac{2.0}{3.193}, \frac{1.75}{3.193}, \frac{1.67}{3.193}, 0, 0] \approx [0.626, 0.548, 0.523, 0, 0]\] -
Documento $D_2$:
[<START>, mostre, me, meus, arquivos, recentes, por, favor]Transição $P_{D2}(t_i)$ $P_{corpus}\;(t_i)$ Razão $\frac{P_{D2}(t_i)}{P_{corpus}\;(t_i)}$ $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$ 1.0 0.50 2.0 $t_2 = (\text{meus}, \text{documentos})$ 0.0 0.571 0.0 $t_3 = (\text{mostre}, \text{me})$ 1.0 0.60 1.67 $t_4 = (\text{meus}, \text{arquivos})$ 1.0 0.429 2.33 $t_5 = (\text{por}, \text{favor})$ 1.0 1.0 1.0 Vetor $D_2$ não normalizado: $\vec{v}_{D2}^{*} = [2.0, 0.0, 1.67, 2.33, 1.0]$
Vetor $D_2$ normalizado (L2):
\[\vert \vec{v}_{D2}^{*} \vert _2 = \sqrt{2.0^2 + 0.0^2 + 1.67^2 + 2.33^2 + 1.0^2} = \sqrt{12.0978} \approx 3.478\] \[\vec{v}_{D2}^{*norm} = [\frac{2.0}{3.478}, 0, \frac{1.67}{3.478}, \frac{2.33}{3.478}, \frac{1.0}{3.478}] \approx [0.575, 0, 0.480, 0.670, 0.288]\] -
Documento $D_3$:
[<START>, por, favor, mostre, meus, documentos, financeiros]Transição $P_{D3}(t_i)$ $P_{corpus}\;(t_i)$ Razão $\frac{P_{D3}(t_i)}{P_{corpus}\;(t_i)}$ $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$ 0.0 0.50 0.0 $t_2 = (\text{meus}, \text{documentos})$ 1.0 0.571 1.75 $t_3 = (\text{mostre}, \text{me})$ 0.0 0.60 0.0 $t_4 = (\text{meus}, \text{arquivos})$ 0.0 0.429 0.0 $t_5 = (\text{por}, \text{favor})$ 1.0 1.0 1.0 Vetor $D_3$ não normalizado: $\vec{v}_{D3}^{*} = [0.0, 1.75, 0.0, 0.0, 1.0]$
Vetor $D_3$ normalizado (L2):
\[\vert \vec{v}_{D3}^{*} \vert _2 = \sqrt{0.0^2 + 1.75^2 + 0.0^2 + 0.0^2 + 1.0^2} = \sqrt{4.0625} \approx 2.016\] \[\vec{v}_{D3}^{*norm} = [0, \frac{1.75}{2.016}, 0, 0, \frac{1.0}{2.016}] \approx [0, 0.868, 0, 0, 0.496]\]
-
-
Visualização e Comparação dos Vetores: vamos visualizar os três vetores normalizados para facilitar a comparação:
Transição $\vec{v}_{D1}^{*norm}$ $\vec{v}_{D2}^{*norm}$ $\vec{v}_{D3}^{*norm}$ $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$ 0.626 0.575 0.000 $t_2 = (\text{meus}, \text{documentos})$ 0.548 0.000 0.868 $t_3 = (\text{mostre}, \text{me})$ 0.523 0.480 0.000 $t_4 = (\text{meus}, \text{arquivos})$ 0.000 0.670 0.000 $t_5 = (\text{por}, \text{favor})$ 0.000 0.288 0.496 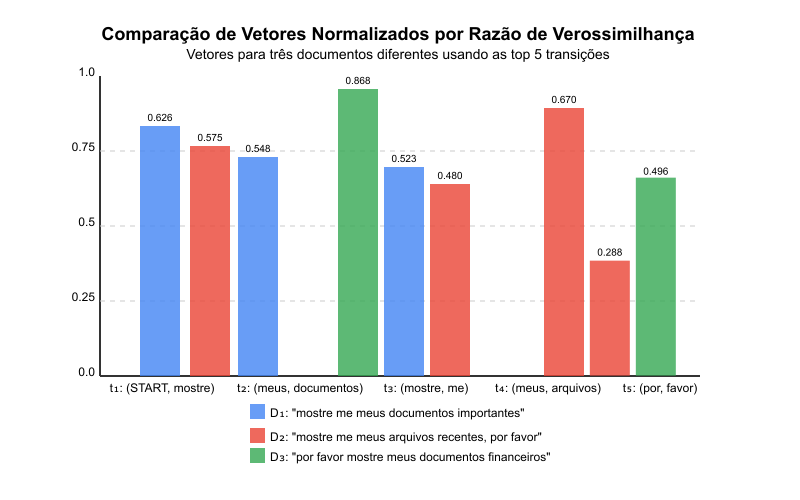 Figura 4: Visualização dos vetores normalizados dos três documentos do nosso exemplo em um gráfico de barras.
Figura 4: Visualização dos vetores normalizados dos três documentos do nosso exemplo em um gráfico de barras. -
Análise dos Vetores: podemos observar características interessantes:
-
Documento $D_1$ tem valores altos para transições relacionadas a “mostre me” e “meus documentos”, mostrando sua ênfase em mostrar documentos.
-
Documento $D_2$ tem o valor mais alto para a transição “meus arquivos”, refletindo seu foco em arquivos. Também tem valores para “mostre me” e “por favor”, mostrando sua estrutura completa.
-
Documento $D_3$ tem o valor mais alto de todos para “meus documentos” (0.868), mas zero para “mostre me” porque sua estrutura começa com “por favor” em vez de “mostre me”. É o único vetor com zero na primeira posição.
-
-
Similaridade entre Documentos: agora que temos os vetores normalizados, podemos calcular a similaridade entre eles. A similaridade de cosseno é uma métrica comum para medir a similaridade entre dois vetores:
-
Similaridade entre $D_1$ e $D_2$: \(\begin{align*} sim(D_1, D_2) &= \vec{v}_{D1}^{*norm} \cdot \vec{v}_{D2}^{*norm} \\ &= 0.626 \times 0.575 + 0.548 \times 0 + 0.523 \times 0.480 \\ &\quad + 0 \times 0.670 + 0 \times 0.288 \\ &= 0.360 + 0 + 0.251 + 0 + 0 \\ &= 0.611 \end{align*}\)
-
Similaridade entre $D_1$ e $D_3$:
\[\begin{align*} sim(D_1, D_3) &= \vec{v}_{D1}^{*norm} \cdot \vec{v}_{D3}^{*norm} \\ &= 0.626 \times 0 + 0.548 \times 0.868 + 0.523 \times 0 \\ &\quad + 0 \times 0 + 0 \times 0.496 \\ &= 0 + 0.476 + 0 + 0 + 0 \\ &= 0.476 \end{align*}\] -
Similaridade entre $D_2$ e $D_3$:
\[\begin{align*} sim(D_2, D_3) &= \vec{v}_{D2}^{*norm} \cdot \vec{v}_{D3}^{*norm} \\ &= 0.575 \times 0 + 0 \times 0.868 + 0.480 \times 0 \\ &\quad + 0.670 \times 0 + 0.288 \times 0.496 \\ &= 0 + 0 + 0 + 0 + 0.143 \\ &= 0.143 \end{align*}\]
-
-
Interpretação das Similaridades
- $D_1$ e $D_2$ são mais similares (0.611), o que faz sentido porque ambos começam com “mostre me” e compartilham várias transições.
- $D_1$ e $D_3$ têm similaridade média (0.476), principalmente devido à transição comum “meus documentos”.
- $D_2$ e $D_3$ são menos similares (0.143), compartilhando apenas a transição “por favor”.
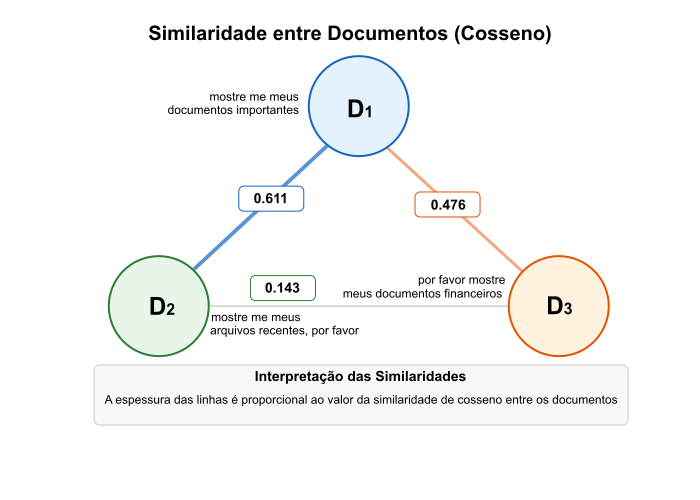 Figura 5: Visualização das similaridades entre os documentos $D_1$, $D_2$ e $D_3$ usando um grafo triangular.
Figura 5: Visualização das similaridades entre os documentos $D_1$, $D_2$ e $D_3$ usando um grafo triangular.
Estas similaridades refletem bem a estrutura real dos documentos, demonstrando a eficácia da vetorização por razão de verossimilhança para capturar diferenças e semelhanças entre documentos com base em suas propriedades sequenciais.
Vetorização Usando o Modelo Agregado e Comparação por Razão de Verossimilhança
Agora que temos o modelo agregado $P_{corpus}\;$, podemos usá-lo para enriquecer a representação vetorial dos documentos. Uma abordagem é usar as probabilidades do corpus $P_{corpus}\;(t_i)$ diretamente como características para as transições selecionadas $t_i$, mas isso cria um vetor de linha de base (baseline) que não diferencia os documentos individuais.
Uma técnica mais poderosa e informativa é a Vetorização por Razão de Verossimilhança, que compara diretamente as probabilidades de transição específicas de um documento ($P_D$) com as probabilidades médias do corpus ($P_{corpus}\;$). Usando as mesmas transições selecionadas $T_{selecionadas} = {t_1, …, t_k}$ que identificamos anteriormente (as $K=5$ mais frequentes no nosso exemplo estendido), o vetor para um documento $D$ é definido como a razão entre as probabilidades do documento e as do corpus para cada transição selecionada:
\[\vec{v}_D^{*} = \left[ \frac{P_D(t_1)}{P_{corpus}\;(t_1)}, \frac{P_D(t_2)}{P_{corpus}\;(t_2)}, ..., \frac{P_D(t_k)}{P_{corpus}\;(t_k)} \right]\]A intuição por trás de cada componente $i$ deste vetor é:
- Se $\frac{P_D(t_i)}{P_{corpus}\;(t_i)} > 1$: a transição $t_i$ é mais provável no documento $D$ do que a média do corpus, indicando uma característica potencialmente distintiva de $D$.
- Se $\frac{P_D(t_i)}{P_{corpus}\;(t_i)} < 1$: a transição $t_i$ é menos provável no documento $D$ do que a média, também uma informação diferencial.
- Se $\frac{P_D(t_i)}{P_{corpus}\;(t_i)} = 1$: a transição $t_i$ ocorre com frequência semelhante em $D$ e no corpus.
É importante notar que $P_D(t_i)$ pode ser $0$ se a transição $t_i = (w_{\text{prev}}, w_{\text{curr}})$ não ocorrer no documento $D$ (ou se $w_{\text{prev}}$ não ocorrer em $D$). Para lidar com casos onde o denominador $P_{corpus}\;(t_i)$ é $0$ (o que significa que a transição nunca ocorre no corpus, improvável para transições selecionadas por frequência, mas possível), técnicas de suavização (como adicionar um pequeno $\epsilon$ ao denominador) podem ser aplicadas, ou podemos simplesmente atribuir um valor padrão (como $0$ ou $1$) para a razão nesses casos raros.
Exemplo de Cálculo dos Vetores de Razão de Verossimilhança
Vamos calcular os vetores $\vec{v}_D^{*}$ para os três primeiros documentos do nosso corpus estendido, usando as $K=5$ transições mais frequentes que identificamos:
- $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$: $P_{corpus}\;(t_1) = 0.50$
- $t_2 = (\text{meus}, \text{documentos})$: $P_{corpus}\;(t_2) = 0.571$
- $t_3 = (\text{mostre}, \text{me})$: $P_{corpus}\;(t_3) = 0.60$
- $t_4 = (\text{meus}, \text{arquivos})$: $P_{corpus}\;(t_4) = 0.429$
- $t_5 = (\text{por}, \text{favor})$: $P_{corpus}\;(t_5) = 1.0$
Documento $D_1$: [<START>, mostre, me, meus, documentos, importantes]
| Transição $t_i$ | $P_{D1}(t_i)$ | $P_{corpus}\;(t_i)$ | Razão $\frac{P_{D1}(t_i)}{P_{corpus}\;(t_i)}$ |
|---|---|---|---|
| $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$ | 1.0 | 0.50 | $1.0 / 0.50 = 2.0$ |
| $t_2 = (\text{meus}, \text{documentos})$ | 1.0 | 0.571 | $1.0 / 0.571 \approx 1.75$ |
| $t_3 = (\text{mostre}, \text{me})$ | 1.0 | 0.60 | $1.0 / 0.60 \approx 1.67$ |
| $t_4 = (\text{meus}, \text{arquivos})$ | 0.0 | 0.429 | $0.0 / 0.429 = 0.0$ |
| $t_5 = (\text{por}, \text{favor})$ | 0.0* | 1.0 | $0.0 / 1.0 = 0.0$ |
Em $D_1$, “por” não aparece, então $P_{D1}(\text{favor} \vert \text{por})$ é considerado $0$.
Vetor $D_1$ (não normalizado): $\vec{v_{D1}^{*}} = [2.0, 1.75, 1.67, 0.0, 0.0]$
Documento $D_2$: [<START>, mostre, me, meus, arquivos, recentes, por, favor]
| Transição $t_i$ | $P_{D2}(t_i)$ | $P_{corpus}\;(t_i)$ | Razão $\frac{P_{D2}(t_i)}{P_{corpus}\;(t_i)}$ |
|---|---|---|---|
| $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$ | 1.0 | 0.50 | $1.0 / 0.50 = 2.0$ |
| $t_2 = (\text{meus}, \text{documentos})$ | 0.0 | 0.571 | $0.0 / 0.571 = 0.0$ |
| $t_3 = (\text{mostre}, \text{me})$ | 1.0 | 0.60 | $1.0 / 0.60 \approx 1.67$ |
| $t_4 = (\text{meus}, \text{arquivos})$ | 1.0 | 0.429 | $1.0 / 0.429 \approx 2.33$ |
| $t_5 = (\text{por}, \text{favor})$ | 1.0 | 1.0 | $1.0 / 1.0 = 1.0$ |
Vetor $D_2$ (não normalizado): $\vec{v}_{D2}^{*} = [2.0, 0.0, 1.67, 2.33, 1.0]$
Documento $D_3$: [<START>, por, favor, mostre, meus, documentos, financeiros]
| Transição $t_i$ | $P_{D3}(t_i)$ | $P_{corpus}\;(t_i)$ | Razão $\frac{P_{D3}(t_i)}{P_{corpus}\;(t_i)}$ |
|---|---|---|---|
| $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$ | 0.0 | 0.50 | $0.0 / 0.50 = 0.0$ |
| $t_2 = (\text{meus}, \text{documentos})$ | 1.0 | 0.571 | $1.0 / 0.571 \approx 1.75$ |
| $t_3 = (\text{mostre}, \text{me})$ | 0.0 | 0.60 | $0.0 / 0.60 = 0.0$ |
| $t_4 = (\text{meus}, \text{arquivos})$ | 0.0 | 0.429 | $0.0 / 0.429 = 0.0$ |
| $t_5 = (\text{por}, \text{favor})$ | 1.0 | 1.0 | $1.0 / 1.0 = 1.0$ |
Vetor $D_3$ (não normalizado): $\vec{v}_{D3}^{*} = [0.0, 1.75, 0.0, 0.0, 1.0]$
Normalização dos Vetores
Assim como na vetorização anterior, para tornar os vetores $\vec{v}_D^{*}$ comparáveis entre si (independentemente da magnitude das razões), aplicamos a normalização, tipicamente a Norma Euclidiana (L2):
\[\vec{v_D^{*norm}} = \frac{\vec{v_D^{*}}}{ \vert \vec{v_D^{*}} \vert _2}\]Na qual,
\[\vert \vec{v_D^{*}} \vert _2 = \sqrt{\sum_{i} (\vec{v_{D,i}^{*}})^2}\]representa a magnitude do vetor.
Aplicando aos nossos exemplos:
-
Para $D_1$:
\[\vert \vec{v}_{D1}^{*} \vert _2 = \sqrt{2.0^2 + 1.75^2 + 1.67^2 + 0.0^2 + 0.0^2} = \sqrt{10.1989} \approx 3.193\] \[\vec{v}_{D1}^{*norm} \approx [0.626, 0.548, 0.523, 0.0, 0.0]\] -
Para $D_2$:
\[\vert \vec{v}_{D2}^{*} \vert _2 = \sqrt{2.0^2 + 0.0^2 + 1.67^2 + 2.33^2 + 1.0^2} = \sqrt{12.0978} \approx 3.478\] \[\vec{v}_{D2}^{*norm} \approx [0.575, 0.0, 0.480, 0.670, 0.288]\] -
Para $D_3$:
\[\vert \vec{v}_{D3}^{*} \vert _2 = \sqrt{0.0^2 + 1.75^2 + 0.0^2 + 0.0^2 + 1.0^2} = \sqrt{4.0625} \approx 2.016\] \[\vec{v}_{D3}^{*norm} \approx [0.0, 0.868, 0.0, 0.0, 0.496]\]
Visualização e Comparação dos Vetores Normalizados
Vamos organizar os vetores normalizados em uma tabela para facilitar a comparação visual:
| Transição Selecionada $t_i$ | $\vec{v}_{D1}^{*norm}$ | $\vec{v}_{D2}^{*norm}$ | $\vec{v}_{D3}^{*norm}$ |
|---|---|---|---|
| $t_1 = (\text{<}\text{START}\text{>}, \text{mostre})$ | 0.626 | 0.575 | 0.000 |
| $t_2 = (\text{meus}, \text{documentos})$ | 0.548 | 0.000 | 0.868 |
| $t_3 = (\text{mostre}, \text{me})$ | 0.523 | 0.480 | 0.000 |
| $t_4 = (\text{meus}, \text{arquivos})$ | 0.000 | 0.670 | 0.000 |
| $t_5 = (\text{por}, \text{favor})$ | 0.000 | 0.288 | 0.496 |
Análise Rápida: observamos como esses vetores capturam características únicas:
- $D_1$ se destaca nas transições $t_1, t_2, t_3$.
- $D_2$ tem forte presença em $t_1, t_3, t_4, t_5$, mas nenhuma em $t_2$.
- $D_3$ é único por ter $0$ em $t_1$ e $t_3$, mas a maior contribuição em $t_2$ e presença em $t_5$.
Comparação entre Documentos
Com os vetores normalizados $\vec{v}_D^{*norm}$, podemos calcular a similaridade entre os documentos usando, por exemplo, a similaridade de cosseno:
\[\text{sim}(D_i, D_j) = \vec{v}_{Di}^{*norm} \cdot \vec{v}_{Dj}^{*norm} = \sum_{l=1}^{k} \vec{v}_{Di, l}^{*norm} \times \vec{v}_{Dj, l}^{*norm}\](A atenta leitora deve lembrar que para vetores já normalizados, o produto escalar é igual à similaridade de cosseno).
Calculando as similaridades:
-
Similaridade entre $D_1$ e $D_2$:
\[sim(D_1, D_2) = (0.626 \times 0.575) + (0.548 \times 0) + (0.523 \times 0.480) + (0 \times 0.670) + (0 \times 0.288)\] \[sim(D_1, D_2) \approx 0.360 + 0 + 0.251 + 0 + 0 = 0.611\] -
Similaridade entre $D_1$ e $D_3$:
\[sim(D_1, D_3) = (0.626 \times 0) + (0.548 \times 0.868) + (0.523 \times 0) + (0 \times 0) + (0 \times 0.496)\] \[sim(D_1, D_3) \approx 0 + 0.476 + 0 + 0 + 0 = 0.476\] -
Similaridade entre $D_2$ e $D_3$:
\[sim(D_2, D_3) = (0.575 \times 0) + (0 \times 0.868) + (0.480 \times 0) + (0.670 \times 0) + (0.288 \times 0.496)\] \[sim(D_2, D_3) \approx 0 + 0 + 0 + 0 + 0.143 = 0.143\]
Interpretação das Similaridades: os resultados mostram que $D_1$ e $D_2$ são os mais similares (ambos começam com “mostre me”), $D_1$ e $D_3$ têm similaridade média (compartilham “meus documentos”), e $D_2$ e $D_3$ são os menos similares (compartilhando apenas a estrutura com “por favor”, que tem peso menor nos vetores normalizados). Isso demonstra como a razão de verossimilhança captura nuances estruturais.
Aplicações da Vetorização por Razão de Verossimilhança
Esta abordagem de vetorização, ao destacar como um documento difere da norma do corpus em termos de sequências de palavras, é particularmente poderosa para várias aplicações:
-
Identificação de estilo: Valores $\gg 1$ ou $\ll 1$ podem indicar características estilísticas distintivas de um autor ou gênero (ex: uso frequente ou raro de certas construções).
-
Detecção de anomalias: Documentos com vetores muito diferentes da maioria (outliers) podem ser facilmente identificados, útil para encontrar spam, plágio ou textos com características incomuns.
-
Classificação de documentos: Os padrões de sobre/sub-representação de transições podem ser fortes indicadores da classe ou categoria de um documento (ex: e-mails formais vs. informais, notícias esportivas vs. políticas).
-
Análise de autoria: Autores tendem a ter “assinaturas linguísticas” nos seus padrões de escrita sequencial, que podem ser capturadas por esses vetores.
-
Comparação entre corpora: A técnica pode ser estendida para comparar corpora inteiros, calculando um $P_{corpus}\;$ para cada um e analisando as razões entre eles para encontrar diferenças sistemáticas na linguagem usada.
Utilidade Geral da Vetorização Probabilística N-gram
As abordagens de vetorização probabilística N-gram que exploramos, desde a construção de matrizes $T_D$ até a comparação por razão de verossimilhança, oferecem uma forma de ir além da simples contagem de palavras (como no TF-IDF). Elas começam a capturar a estrutura sequencial da linguagem, focando nas probabilidades de como as palavras se seguem umas às outras.
Embora limitadas pelo contexto local (especialmente em ordens baixas como $N=2$, bigramas), essas técnicas são fundamentais para entender a evolução dos modelos de linguagem. Elas fornecem representações que podem ser usadas em tarefas como:
- Classificação de texto mais precisa, considerando padrões locais.
- Detecção de outliers baseada em padrões sequenciais incomuns.
- Análise de estilo e autoria.
- Modelagem de linguagem simples e geração de texto (usando $T_{corpus}\;$ para prever ou amostrar a próxima palavra).
A capacidade de capturar não apenas a presença de palavras, mas a probabilidade de suas sequências (incluindo o início do texto com tokens como <START>), fornece uma representação rica e diferenciada para tarefas de PLN, preparando o terreno para modelos mais avançados que buscam superar a limitação do contexto local.
