Transformers - Prestando Atenção

Superando Limitações Locais: Construindo a Ponte para a Atenção
Em outro porto, navegamos pelos modelos probabilísticos clássicos para vetorização de sequências, como as Cadeias de Markov e os Modelos **N-gram. Vimos como estes modelos são capazes de capturar a dependência local estimando a probabilidade de uma palavra, $w_t$, com base em suas $N - 1$ vizinhas imediatas, $P(w_t \vert w_{t-N+1}, …, w_{t-1})$. As técnicas que estudamos são capazes de fornecer representações ricas, como a **Vetorização por Razão de Verossimilhança, que compara padrões locais de um documento com os padrões gerais do corpus. Mas, como uma luneta danificada, não permitem uma visão completa.
A própria natureza desses modelos, encapsulada na Propriedade de Markov, impõe uma limitação significativa: a dificuldade em capturar dependências de longo alcance. Esta limitação é precisamente o que os modelos baseados em mecanismos de atenção, como os Transformers, procuram superar, permitindo que cada palavra na sequência preste atenção a qualquer outra palavra, independentemente da distância entre elas. A esforçada leitora deveria ler este parágrafo novamente, com atenção, e refletir sobre o que ele significa. A ideia de que cada palavra pode prestar atenção a qualquer outra palavra, independentemente da distância entre elas, é a bússola que a guiará no entendimento dos Transformers.
A Propriedade de Markov é um conceito fundamental em processos estocásticos e modelagem de sequências. Esta propriedade estabelece que a probabilidade de um estado futuro depende apenas do estado presente, e não de estados anteriores da sequência.
Em termos mais formais, para uma sequência de variáveis aleatórias, como palavras em um texto, $X_1, X_2, …, X_n$, a Propriedade de Markov afirma que:
\[P(X_{n+1} = x \vert X_1 = x_1, X_2 = x_2, ..., X_n = x_n) = P(X_{n+1} = x \vert X_n = x_n)\]
Para ir além das informações obtidas com a Propriedade de Markov e entender o significado completo, ou prever a próxima palavra, em situações da linguagem real, precisaremos relacionar palavras que estão muito distantes entre si em uma determinada sequência de texto.
A dedicada leitora deve considerar que, a solução inocente, aumentar a ordem $N$ nos modelos N-gram para tentar alcançar contextos mais longos, será impraticável devido à esparsidade dos dados que resultará desta solução. Afinal, não deve ser difícil de entender que as combinações de $N$ palavras ficam cada vez mais raras e que o número de estados possíveis, crescerá quase exponencialmente, a maldição da dimensionalidade. Sendo assim, a pergunta que fica é:
Como podemos capturar dependências de longo alcance sem aumentar a ordem dos N-grams?
Crescimento Exponencial em N-gramas e Esparsidade de Dados
Se temos um vocabulário de tamanho $\vert V \vert $, o número de possíveis N-gramas únicos será dado por:
\[\vert V \vert^N\]Para um vocabulário típico de $50.000$ palavras:
- Bigramas: $50.000^2 = 2.5 \times 10^9$ combinações possíveis
- Trigramas: $50.000^3 = 1.25 \times 10^{14}$ combinações possíveis
- Tetragramas: $50.000^4 = 6.25 \times 10^{18}$ combinações possíveis
A Lei de Zipf governa a distribuição de frequências de palavras naturais. A frequência da $k$-ésima palavra mais comum será aproximadamente:
\[f(k) \propto \frac{1}{k^s}\]Na qual $s \approx 1$ para linguagem natural. Isso significa que a maioria das palavras, e consequentemente N-grams, são extremamente raras.
A Lei de Zipf implica que a maioria dos N-grams terá uma frequência muito baixa, resultando em uma distribuição altamente esparsa. Por exemplo, mesmo com um corpus massivo de $10^9$ tokens, a probabilidade de observar qualquer N-gram específico torna-se caracteristicamente pequena.
Conforme $N$ aumenta, enfrentamos a maldição da dimensionalidade: mesmo com corpora massivos, digamos $10^9$ tokens, a densidade de dados no espaço de N-grams diminui exponencialmente. A probabilidade de observar qualquer N-gram específico tende a ser muito próxima de zero.
Para $N \geq 4$, a maioria dos N-grams possíveis nunca aparece nos dados de treinamento, resultando em:
- Estimativas de probabilidade zero para sequências válidas mas não observadas;
- Necessidade de técnicas de suavização, no inglês usamos a palavra smoothing, cada vez mais sofisticadas;
- Problemas de generalização.
A solução moderna contorna isso através de representações distribuídas e arquiteturas neurais que aprendem representações de menor dimensionalidade, capturando dependências de longo alcance sem enfrentar diretamente a explosão combinatorial do espaço de N-grams.
Nesta jornada, apresentada no Mapa Mental 1, percorreremos uma rota entre a visão local dos N-grams e os mecanismos mais sofisticados que permitem aos Transformers lidar com essas dependências. Nosso primeiro porto será conceitual. Iremos navegar pela ideia de Agregação de Características de Pares. Esta técnica deverá permitir que possamos considerar a influência de todos os pares formados pela palavra atual, $w_t$, e cada palavra $w_i$ que a precede ($i < t$), efetivamente saltando sobre o contexto intermediário.
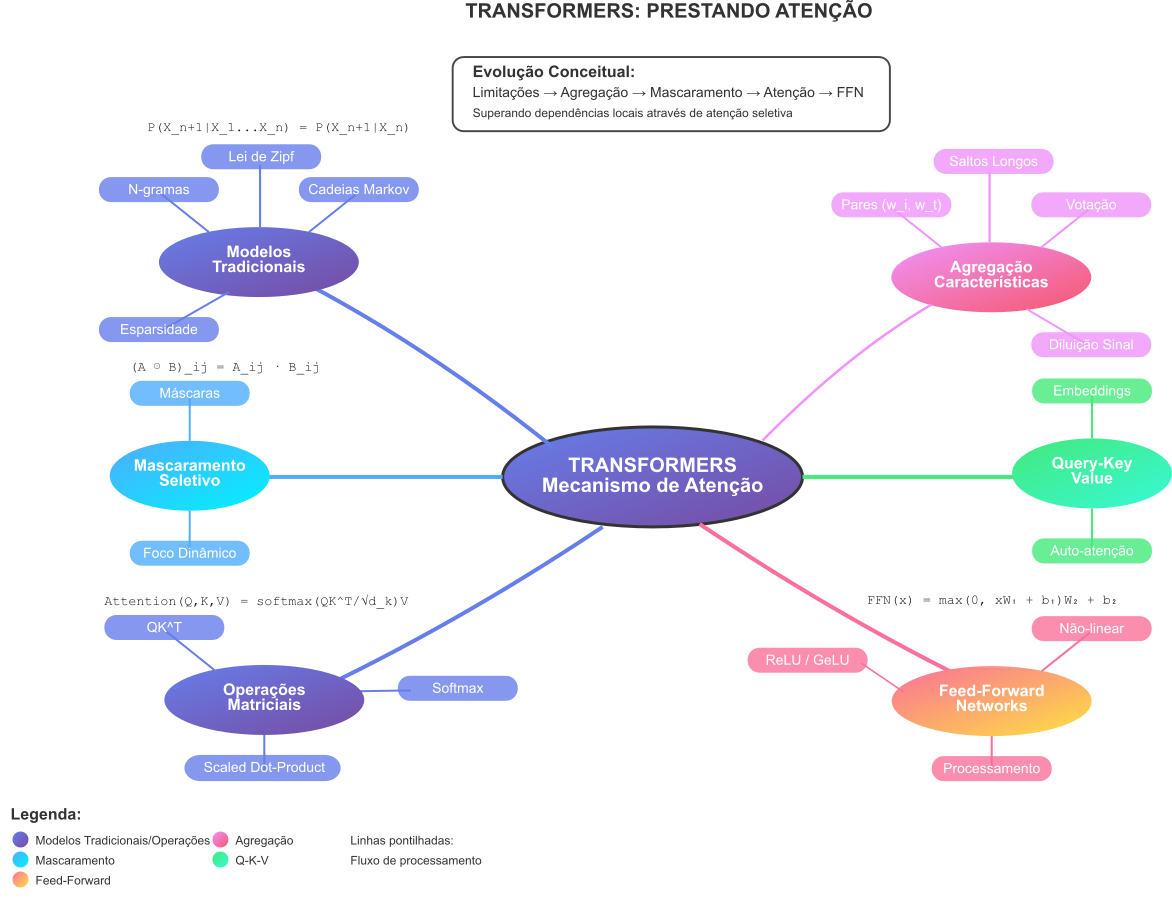
Mapa Mental 1: Roteiro da jornada para entender os Transformers. A jornada começa com a visão local dos N-grams e avança para a introdução de mecanismos de atenção, culminando na compreensão dos Transformers.
Minha esperança é que a ávida leitora seja capaz de entender como essa agregação funciona, suas vantagens e limitações. Serão justamente estas limitações do modelo de Agregação de Características de Pares que impulsionarão nossa jornada até a introdução dos conceitos de atenção seletiva e mascaramento. Este será o porto mais importante desta jornada. Quando chegarmos lá será possível ver como o conceito de foco, manter a atenção no que interessa, pode ser implementada através de operações matriciais e como a informação contextual resultante pode ser processada por Redes Feed-Forward (FFN).
Com cuidado e bom tempo, ao final desta jornada, teremos desvendado a intuição teórica e os componentes tecnológico que sustentam a revolução trazida pelos Transformers.
Agregação de Características de Pares
Por tudo que vimos, podemos dizer que aumentar a ordem $N$ nos modelos N-gram/Markovianos é uma estratégia limitada para capturar o contexto necessário em linguagem natural devido à maldição da dimensionalidade e à esparsidade dos dados. Precisamos de uma abordagem diferente para lidar com dependências que podem se estender por muitas palavras.
A sagaz leitora não deve esquecer que queremos transformar linguagem natural, no formato de texto, em algo que o computador possa manipular. Nossa escolha ainda está no processo de vetorização de textos. Deste ponto em diante, a criativa leitora deve considerar que nosso sistema precisa lidar com frases complexas. Entretanto, estamos criando conhecimento e desvendando mistérios. Então, em benefício do entendimento, vamos começar considerando dois documentos, frases, simples, e que cada um ocorre com igual probabilidade de $50\%$:
- $D_1$ =
Verifique o log do programa e descubra se ele foi executado, por favor.; - $D_2$ =
Verifique o log da bateria e descubra se ela acabou, por favor..
Neste cenário que acabamos de criar, para determinar a sequência correta de palavras após descubra se, precisamos resolver a referência pronominal. Se o log mencionado anteriormente era do programa, substantivo masculino, o pronome correto é ele e a ação subsequente é foi executado. Se o log era da bateria, substantivo feminino, o pronome correto é ela e a ação é acabou.
Será uma palavra, programa ou bateria, que determinará o pronome e o verbo seguintes. Esta palavra importante está significativamente distante na sequência de palavras. Um modelo de Markov tradicional exigiria uma ordem $N$ inviável, $N > 8$, para capturar essa dependência com os modelos que vimos antes em qualquer texto do mundo real.
Para superar a visão estritamente local dos modelos N-gram, discutidos em detalhe no artigo anterior, foram, ao longo do tempo, propostas algumas alternativas interessantes:
-
Modelos Probabilísticos Estendidos
Hidden Markov Models (HMMs) RABINER, L. R. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE, v. 77, n. 2, p. 257-286, 1989.
Os HMMs introduziram estados ocultos que podem capturar informações contextuais além da observação imediata, permitindo modelar dependências mais complexas que os modelos Markovianos simples.
-
Modelos Neurais de Linguagem
Neural Probabilistic Language Models BENGIO, Y. et al. A neural probabilistic language model. Journal of Machine Learning Research, v. 3, p. 1137-1155, 2003.
Pioneiro no uso de redes neurais para modelagem de linguagem, este trabalho introduziu embeddings de palavras e demonstrou como redes neurais podem capturar similaridades semânticas.
-
Arquiteturas Recorrentes
Recurrent Neural Networks (RNNs) ELMAN, J. L. Finding structure in time. Cognitive Science, v. 14, n. 2, p. 179-211, 1990.
As RNNs introduziram a capacidade de manter estado interno, teoricamente permitindo memória de toda a sequência anterior, embora na prática sofram com o problema de gradientes que desaparecem.
Long Short-Term Memory (LSTM) HOCHREITER, S.; SCHMIDHUBER, J. Long short-term memory. Neural Computation, v. 9, n. 8, p. 1735-1780, 1997.
As LSTMs resolveram o problema de gradientes que desaparecem através de gates especializados, permitindo capturar dependências de longo prazo de forma mais efetiva.
Gated Recurrent Units (GRUs) CHO, K. et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In: CONFERENCE ON EMPIRICAL METHODS IN NATURAL LANGUAGE PROCESSING, 2014, Doha. Proceedings […]. Doha: ACL, 2014. p. 1724-1734.
Uma simplificação das LSTMs que mantém a capacidade de modelar dependências longas com menor complexidade computacional.
-
Modelos Sequence-to-Sequence
Encoder-Decoder Architecture SUTSKEVER, I.; VINYALS, O.; LE, Q. V. Sequence to sequence learning with neural networks. In: ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS, 27., 2014, Montreal. Proceedings […]. Montreal: NIPS, 2014. p. 3104-3112.
Introduziu a arquitetura encoder-decoder que separa a compreensão da sequência de entrada da geração da sequência de saída.
-
Primeiros Mecanismos de Atenção
Neural Machine Translation with Attention BAHDANAU, D.; CHO, K.; BENGIO, Y. Neural machine translation by jointly learning to align and translate. In: INTERNATIONAL CONFERENCE ON LEARNING REPRESENTATIONS, 3., 2015, San Diego. Proceedings […]. San Diego: ICLR, 2015.
Pioneiro na introdução do mecanismo de atenção, permitindo que o decoder acesse diretamente diferentes partes da sequência de entrada.
Effective Attention Mechanisms LUONG, M. T.; PHAM, H.; MANNING, C. D. Effective approaches to attention-based neural machine translation. In: CONFERENCE ON EMPIRICAL METHODS IN NATURAL LANGUAGE PROCESSING, 2015, Lisbon. Proceedings […]. Lisbon: ACL, 2015. p. 1412-1421.
Refinamento dos mecanismos de atenção, introduzindo diferentes tipos de funções de score para calcular a atenção.
-
Abordagens Convolucionais
Convolutional Neural Networks for NLP KIM, Y. Convolutional neural networks for sentence classification. In: CONFERENCE ON EMPIRICAL METHODS IN NATURAL LANGUAGE PROCESSING, 2014, Doha. Proceedings […]. Doha: ACL, 2014. p. 1746-1751.
Aplicação de CNNs para capturar padrões locais em diferentes escalas através de filtros de diferentes tamanhos.
Cada uma dessas abordagens representou um passo incremental na direção de superar as limitações dos modelos N-gram, culminando no desenvolvimento da arquitetura Transformer que combina eficiência computacional com capacidade de modelar dependências arbitrariamente longas.
Vamos nos concentrar em uma abordagem na qual A ideia central será:
ao tentar prever a palavra que segue a palavra atual, $w_t$, em vez de depender apenas do contexto imediatamente anterior, como no par $(w_{t-1}, w_t)$ para bigramas ou a janela fixa dos **N-grams**, vamos considerar a influência potencial de todas as palavras $w_i$ que apareçam antes de $w_t$ na sequência.
Em outras palavras, o que estamos propondo é um método que permita analisar a contribuição de cada par $(w_i, w_t)\;$. No qual, o índice $i$ varia desde o início da sequência até a posição anterior a $t$ para todo $i : 0 \le i < t$.
Olhar o problema por essa perspectiva permitirá saltar sobre o texto intermediário que pode existir entre $w_i$ e $w_t$. Ao fazer isso, abrimos a possibilidade de capturar dependências e relações semânticas de longo alcance, que são inacessíveis aos modelos N-gram tradicionais devido à sua janela de contexto fixa e local. E, é claro, aos problemas relacionados à maldição da dimensionalidade.
Essa mudança conceitual implicará em uma reinterpretação da matriz de transição. Neste caso, as linhas da matriz não representarão um estado probabilístico: o contexto imediato $w_{t-1}$ ou $[w_{t-2}, w_{t-1}]$ no qual as probabilidades de transição devem somar $1$. Em vez disso, cada linha poderá ser vista como uma característica, do inglês feature, que será definida por um par específico $(w_i, w_t)$ que ocorreu na sequência independente da distância entre $w_i$ e $w_t$. O valor na coluna $j$ dessa linha passa a representar um voto ou o peso que essa característica específica atribui à palavra $w_j$ como sendo a próxima palavra $(w_{t+1})$.
A amável leitora vai ouvir falar muito em features, neste texto, na academia e no populacho. O conceito de feature como uma característica do texto anterior a uma determinada palavra, que permite definir qual palavra a seguirá, é tão importante no processamento de linguagem natural que praticamente se tornou uma medida de desempenho.
Pense sobre as features da seguinte forma: cada par $(w_i, w_t)$ representa uma característica que possui um determinado grau de contribuição na previsão da próxima palavra. O valor associado a essa característica indica o quanto o par $(w_i, w_t)$ contribui para a definição de cada palavra candidata a ser a próxima.
Para construir a intuição, usaremos frequentemente a analogia de um voto, embora o termo técnico mais geral seja peso. Não se preocupe, a palavra peso se tornará mais prevalente à medida que avançarmos para mecanismos mais complexos.
Ainda estamos considerando os documentos:
- $D_1$ =
Verifique o log do programa e descubra se ele foi executado, por favor.; - $D_2$ =
Verifique o log da bateria e descubra se ela acabou, por favor..
A Figura 1 ilustra o conceito de votação de características de pares com saltos. Cada par $(w_i, w_t)$ vota em uma palavra candidata $w_k$ como a próxima palavra a seguir $w_t$. O valor do voto é o peso que essa característica atribui à palavra candidata.
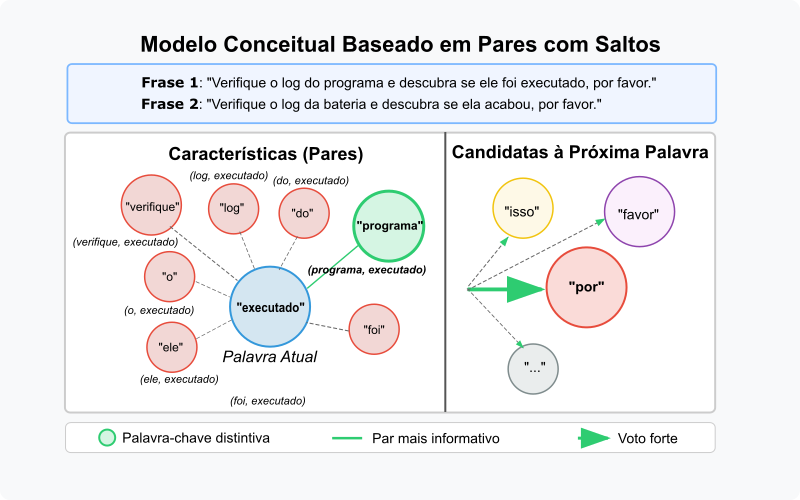 Figura 1: Modelo conceitual hipotético baseado em pares com saltos. As linhas representam características (pares como
Figura 1: Modelo conceitual hipotético baseado em pares com saltos. As linhas representam características (pares como (programa, executado) ou (bateria, executado)). Os valores apresentados são “votos” para a próxima palavra (ex: “por”). Apenas pesos não-zero relevantes são mostrados. A ilustração foca na predição da palavra após executado no contexto da primeira frase.
A Figura 1 ilustra a ideia de feature como fator para a previsão da palavra após executado, no primeiro exemplo de frase: ... log do programa ... ele foi executado .... Várias características, pares formados por executado e palavras anteriores como verifique, o, log, do, programa, ele, foi, etc. estão ativas. Cada uma delas vota nas possíveis próximas palavras. A palavra com mais votos, ou com peso maior, será a escolhida como a próxima palavra. No exemplo, o par (programa, executado) tem um voto alto para por, enquanto o par (bateria, executado) tem um voto baixo, ou zero. Isso significa que, no contexto da frase, por é uma escolha mais provável do que favor ou outras palavras. Assim, temos:
-
Características como
(programa, executado)dariam um voto forte parapor, pois essa sequência (programa ... executado por favor) é plausível e ocorre na primeira frase. -
Características como
(bateria, executado)dariam voto zero, ou muito baixo, parapor, pois essa combinação não ocorre no nosso exemplo, Na segunda frase temosbateria ... ela acabou. -
Características menos informativas, como
(o, executado)ou(log, executado), podem ter votos distribuídos, ou votos mais fracos. Ver apenasooulogantes deexecutadonão ajuda muito a distinguir entre as frases originais ou a prever a palavra seguinte.
Para fazer uma previsão, somamos os votos de todas as características ativas, pares formados pela palavra atual e todas as palavras anteriores na sequência específica, para cada palavra candidata a ser a próxima. A palavra com a maior soma de votos será a palavra escolhida.
No documento $D_2$, Verifique o log do programa e descubra se ele foi executado: as características ativas relevantes para prever a palavra após executado incluem pares como (verifique, executado), (o, executado), (log, executado), (do, executado), (programa, executado), (e, executado), (descubra, executado), (se, executado), (ele, executado), (foi, executado). Se somarmos os votos hipotéticos. Sendo assim, o par informativo (programa, executado) tem um voto alto para por, e outros pares menos informativos têm votos menores ou distribuídos, a palavra por provavelmente acumulará o total de votos mais alto, tornando-se a previsão correta para esta sequência. A Figura 2 ilustra este conceito de forma mais detalhada.
 Figura 2: A figura ilustra o mecanismo de votação de características hipotético para predição da próxima palavra em um modelo baseado em pares com saltos. No exemplo, no contexto da frase
Figura 2: A figura ilustra o mecanismo de votação de características hipotético para predição da próxima palavra em um modelo baseado em pares com saltos. No exemplo, no contexto da frase Verifique o log do programa e descubra se ele foi executado, está sendo prevista a palavra que segue executado .
Esta abordagem, embora ainda baseada em pares de palavras, oferece uma forma de incorporar contexto de longo alcance de maneira seletiva, focando apenas nas palavras anteriores que são relevantes para a predição atual.
A implementação pode utilizar estruturas de dados semelhantes às dos modelos N-gram tradicionais, como bigramas ou trigramas, mas a lógica de treinamento e predição se transforma: em vez de considerar apenas o contexto imediato, o modelo soma os votos de todos os pares $(w_i, w_t)$ que estão presentes na sequência atual, onde $w_i$ representa qualquer palavra anterior e $w_t$ a palavra atual.
Para que a cativa leitora possa entender como os valores de votos apresentados na Figura 2 são calculados, precisamos detalhar a matemática conceitual por trás da abordagem de Agregação de Características de Pares. É importante notar que os valores na figura são ilustrativos, hipotéticos, que foram criados para facilitar o entendimento da ideia de que diferentes pares têm pesos diferentes. Um corpus de treinamento real conteria muito mais dados.
Todo o conceito que vimos até aqui pode ser reduzido a três passos:
-
Coleta de Evidências (Contagem): durante a fase de treinamento, que no nosso caso conceitual será apenas analisar as frases de exemplo, o modelo observa todas as ocorrências de sequências de três palavras $(w_i, w_t, w_{t+1})$. Para cada par $(w_i, w_t)$ que aparece na sequência, ele registra qual palavra $w_{t+1}$ o seguiu. Nesta fase, mantemos uma contagem, $C(w_i, w_t, w_{t+1})\;$, de quantas vezes vimos a palavra $w_{t+1}$ aparecer imediatamente após a palavra $w_t$, dado que $w_i$ apareceu em alguma posição anterior a $t$. Se as sequências tiverem pesos, como no exemplo que definimos com cada frase tendo peso $0.5$, somamos esses pesos em vez de apenas contar $1$ para cada ocorrência.
Para as sequências de treinamento do nosso corpus, temos:
- $D_1 =$
Verifique o log do programa e descubra se ele foi executado, por favor.(peso 0.5) - $D_2 =$
Verifique o log da bateria e descubra se ela acabou, por favor.(peso 0.5)
Contagens para $(w_i, \text{executado}, w_{t+1})$:
$w_i$ $w_t$ $w_{t+1}$ Ocorrências Peso Total verifique executado por 1 0.5 o executado por 1 0.5 log executado por 1 0.5 do executado por 1 0.5 programa executado por 1 0.5 e executado por 1 0.5 descubra executado por 1 0.5 se executado por 1 0.5 ele executado por 1 0.5 foi executado por 1 0.5 Contagens para $(w_i, \text{acabou}, w_{t+1})$:
$w_i$ $w_t$ $w_{t+1}$ Ocorrências Peso Total verifique acabou por 1 0.5 o acabou por 1 0.5 log acabou por 1 0.5 da acabou por 1 0.5 bateria acabou por 1 0.5 e acabou por 1 0.5 descubra acabou por 1 0.5 se acabou por 1 0.5 ela acabou por 1 0.5 Observação: Cada contagem $C(w_i, w_t, w_{t+1}) = 0.5$ porque cada sequência tem peso 0.5 e cada tripla aparece exatamente uma vez em sua respectiva sequência.
- $D_1 =$
-
Normalização por Par (Cálculo dos Votos): para cada par específico $(w_i, w_t)$ que ocorreu no treinamento, calculamos o voto que este par dá para uma possível próxima palavra $w_k$. Esse voto é a frequência relativa, ou probabilidade condicional estimada, de $w_k$ ocorrer após $(w_i, w_t)\;$, baseada nas contagens. A fórmula para o voto será dada por:
\[\text{Voto}(w_k \vert w_i, w_t) = \frac{C(w_i, w_t, w_k)}{\sum_{w'} C(w_i, w_t, w')}\]Na qual, a soma no denominador $\sum_{w’} C(w_i, w_t, w’)\;\,$ será feita sobre todas as palavras $w’$ que foram observadas seguindo o par $(w_i, w_t)$ no corpus de treinamento. Isso garante que a soma dos votos de um par específico $(w_i, w_t)$ para todas as possíveis palavras seguintes seja $1$.
Vamos calcular os votos para o par (
programa,executado) usando nossos dados reais:Dados de Contagem Coletados:
- C(
programa,executado,por) = $0.5$ (aparece $1$ vez no documento $D_1$ com peso $0.5$); - Nenhuma outra palavra segue este par no corpus.
Aplicando a Fórmula de Normalização:
-
Calculando o denominador (soma de todas as contagens para este par):
\[\Sigma C(programa, executado, w') = C(programa, executado, por) = 0.5\] -
Calculando o voto para
\[Voto(por \vert programa, executado) = \frac{C(programa, executado, por)}{\Sigma C(programa, executado, w')}\] \[= \frac{0.5 }{0.5} = 1.0\]por: -
Calculando o voto para “favor” (que não aparece após este par):
\[Voto(favor \vert programa, executado) = \frac{C(programa, executado, favor)}{ \Sigma C(programa, executado, w')}\] \[= 0 / 0.5 = 0.0\]
Verificação da Propriedade de Normalização:
\[Voto(por \vert programa, executado) + Voto(favor \Vert programa, executado)\] \[= 1.0 + 0.0 = 1.0\]Corretamente normalizada. Voto para
por: $1.0$ (100% das vezes queprogramaeexecutadoaparecem juntos, a próxima palavra épor).Interpretação: No nosso corpus limitado, 100% das vezes que vemos
programa ... executado, a próxima palavra épor. - C(
-
Agregação na Predição: quando queremos prever a palavra após $w_t$ em uma nova sequência, um documento qualquer que não está no corpus de treinamento, identificamos todos os pares $(w_i, w_t)$ formados pela palavra atual $w_t$ e cada palavra anterior $w_i$ na sequência. Em seguida, somamos os votos pré-calculados durante o treinamento, $\text{Voto}(w_k \vert w_i, w_t)\;\,$ para cada palavra candidata $w_k$:
\[Score(w_k \vert \text{sequência até } w_t) = \sum_{i \text{ tal que } w_i \text{ precede } w_t} Voto(w_k \vert w_i, w_t)\]A palavra $w_k$ com o maior $Score$ agregado é a previsão do modelo. A Figura 2 ilustra a etapa antes dessa agregação final, mostrando os votos individuais $\text{Voto}(w_k \vert w_i, w_t)$ para $w_t = \text{“executado”}$ e vários $w_i$.
Eu parti de um exemplo simples, livre, leve e solto, para que a esforçada leitora tenha uma chance maior de entender a ideia. Mas, a criativa leitora deve extrapolar essa abordagem e entender que ela pode ser aplicada a sequências muito mais longas e complexas.
O conceito que deve permanecer é que, ao considerar todos os pares $(w_i, w_t)\;$, podemos capturar dependências de longo alcance que seriam impossíveis com um modelo N-gram tradicional. Talvez um exemplo mais complexo ajude a fixar a ideia.
Exemplo Detalhado: Modelo de Agregação de Características de Pares
Mesmo que o título desta seção seja exemplo detalhado, eu vou ignorar que no mundo real, passaríamos o corpus por alguns processos de preparação de texto antes da aplicação de qualquer algoritmo. Sendo assim, para este exemplo a esforçada leitora deve considerar um corpus de treinamento com os $5$ documentos a seguir:
- $D_1 =\;$
Verifique o log do programa e descubra se ele foi executado, por favor.; - $D_2 =\;$
Verifique o log da bateria e descubra se ela acabou, por favor.; - $D_3 =\;$
O programa foi executado com sucesso, por isso não precisa verificar novamente.; - $D_4 =\;$
A bateria foi substituída, por isso está funcionando corretamente.; - $D_5 =\;$
Ele executou o programa, por isso obteve os resultados esperados..
Cada documento tem peso igual a $0.2$ no corpus. Isso quer dizer que estes documentos são igualmente prováveis no nosso sistema. Podemos calcular explicitamente as probabilidades e valores para o nosso modelo.
1. Coleta de Evidências (Contagem)
Primeiro, precisamos contar todas as ocorrências de triplas $(w_i, w_t, w_{t+1})\;$, na qual:
- $w_i$ é uma palavra anterior na sequência;
- $w_t$ é a palavra atual para a qual queremos prever a próxima;
- $w_{t+1}$ é a palavra que segue $w_t$.
Para este exemplo, vamos tentar prever a palavra após a palavra executado em diferentes contextos.
- Contagens para $(w_i, \text{executado}, w_{t+1})$
| $w_i$ | $w_t$ | $w_{t+1}$ | Ocorrências | Peso Total |
|---|---|---|---|---|
| programa | executado | por | 1 | 0.2 |
| foi | executado | por | 1 | 0.2 |
| ele | executado | por | 1 | 0.2 |
| programa | executado | com | 1 | 0.2 |
| foi | executado | com | 1 | 0.2 |
2. Normalização por Par (Cálculo dos Votos)
Para cada par $(w_i, w_t)\;$, calculamos o voto para cada possível próxima palavra $w_k$ usando:
\[\text{Voto}(w_k \vert w_i, w_t) = \frac{C(w_i, w_t, w_k)}{\sum_{w'} C(w_i, w_t, w')}\]-
Cálculo para o par $(\text{programa}, \text{executado})$
\[\text{Voto}(\text{por} \vert \text{programa}, \text{executado}) = \frac{0.2}{0.2 + 0.2} = \frac{0.2}{0.4} = 0.5\] \[\text{Voto}(\text{com} \vert \text{programa}, \text{executado}) = \frac{0.2}{0.2 + 0.2} = \frac{0.2}{0.4} = 0.5\] -
Cálculo para o par $(\text{foi}, \text{executado})$
\[\text{Voto}(\text{por} \vert \text{foi}, \text{executado}) = \frac{0.2}{0.2 + 0.2} = \frac{0.2}{0.4} = 0.5\] \[\text{Voto}(\text{com} \vert \text{foi}, \text{executado}) = \frac{0.2}{0.2 + 0.2} = \frac{0.2}{0.4} = 0.5\] -
Cálculo para o par $(\text{ele}, \text{executado})$
\[\text{Voto}(\text{por} \vert \text{ele}, \text{executado}) = \frac{0.2}{0.2} = 1.0\] \[\text{Voto}(\text{com} \vert \text{ele}, \text{executado}) = \frac{0}{0.2} = 0.0\]
3. Agregação na Predição
Nosso próximo passo é prever a próxima palavra após executado em uma nova sequência:
Verifique se o programa foi executado ...
Antes de qualquer coisa a atenta leitora deve observar que Verifique se o programa foi executado ... não faz parte do corpus de treinamento. Portanto, não temos certeza de como o modelo irá se comportar. Vamos analisar os pares $(w_i, w_t)$ formados por executado e as palavras anteriores na sequência. Neste caso, as palavras anteriores relevantes são: verifique, se, o, programa, foi.
Focaremos nos pares que já vimos no treinamento:
| Par $(w_i, w_t)$ | Voto para por |
Voto para com |
|---|---|---|
| (programa, executado) | 0.5 | 0.5 |
| (foi, executado) | 0.5 | 0.5 |
Agregando estes votos:
\[\text{Score}(\text{por}) = 0.5 + 0.5 = 1.0\] \[\text{Score}(\text{com}) = 0.5 + 0.5 = 1.0\]Neste caso, o modelo não consegue distinguir claramente entre por e com baseado apenas nas duas palavras-chave. Isso demonstra uma limitação do modelo quando apenas alguns pares são informativos.
Se incluirmos mais contexto, como em outra sequência nova:
Verifique se ele foi executado ...
Então temos:
| Par $(w_i, w_t)$ | Voto para por |
Voto para com |
|---|---|---|
| (ele, executado) | 1.0 | 0.0 |
Neste caso:
\[\text{Score}(\text{por}) = 1.0\] \[\text{Score}(\text{com}) = 0.0\]O modelo prevê claramente por como a próxima palavra.
Este exemplo ilustra como a presença de palavras-chave distintivas (ele vs. programa ou foi) pode alterar significativamente a previsão, demonstrando como o modelo captura dependências de longo alcance.
Implementação em C++
O código C++ apresentado abaixo, encapsulado na classe PairwiseFeatureAggregator, implementa precisamente os passos que acabamos de detalhar no exemplo. O método addSequence corresponde à coleta de evidências (Passo 1), normalizeVotes executa o cálculo dos votos normalizados por par (Passo 2), e predictNextWord realiza a agregação desses votos para efetuar a predição em novas sequências (Passo 3).
#include <iostream> ///< Para entrada e saída padrão (std::cout).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de sequências.
#include <string> ///< Para std::string, usado em palavras e mensagens.
#include <unordered_map> ///< Para std::unordered_map, usado no armazenamento de transições.
#include <map> ///< Para std::map, usado na ordenação de predições.
#include <set> ///< Para std::set, usado no armazenamento do vocabulário.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
/**
* @class PairwiseFeatureAggregator
* @brief Uma classe para modelar transições de palavras com base em pares com saltos.
*
* Esta classe implementa um modelo que associa pares de palavras (anterior, atual) a palavras seguintes,
* acumulando pesos (votos) para prever a próxima palavra em uma sequência. Os pesos são normalizados
* para cada par (anterior, atual) como probabilidades condicionais.
*/
class PairwiseFeatureAggregator {
private:
/**
* @brief Estrutura para armazenar transições: transitions[palavra_anterior][palavra_atual][proxima_palavra] -> peso.
*/
std::unordered_map<std::string,
std::unordered_map<std::string,
std::unordered_map<std::string, double>>> transitions;
std::set<std::string> vocabulary; ///< Vocabulário global de palavras.
public:
/**
* @brief Adiciona uma sequência ao modelo, acumulando pesos para transições.
* @param sequence Vetor de strings representando a sequência de palavras.
* @param weight Peso a ser atribuído à sequência (padrão é 1.0).
*/
void addSequence(const std::vector<std::string>& sequence, double weight = 1.0) {
if (sequence.size() < 3) return; // Necessário pelo menos (anterior, atual, próxima)
// Adicionar palavras ao vocabulário
for (const auto& word : sequence) {
vocabulary.insert(word);
}
// Para cada posição atual, associar pares (anterior, atual) à próxima palavra
for (size_t current_pos = 1; current_pos < sequence.size() - 1; ++current_pos) {
const std::string& current_word = sequence[current_pos];
const std::string& next_word = sequence[current_pos + 1];
for (size_t prev_pos = 0; prev_pos < current_pos; ++prev_pos) {
const std::string& prev_word = sequence[prev_pos];
transitions[prev_word][current_word][next_word] += weight;
}
}
}
/**
* @brief Normaliza os pesos (votos) para cada par (anterior, atual) como probabilidades.
*/
void normalizeVotes() {
for (auto& [prev_word, inner_map1] : transitions) {
for (auto& [current_word, inner_map2] : inner_map1) {
double total_votes = 0.0;
for (auto const& [next_word, vote] : inner_map2) {
total_votes += vote;
}
if (total_votes > 0) {
for (auto& [next_word, vote] : inner_map2) {
inner_map2[next_word] /= total_votes;
}
}
}
}
}
/**
* @brief Prediz a próxima palavra com base na sequência fornecida.
* @param sequence Vetor de strings representando a sequência de entrada.
* @return Mapa ordenado de palavras candidatas para a próxima palavra e seus pesos acumulados.
*/
std::map<std::string, double> predictNextWord(const std::vector<std::string>& sequence) const {
std::map<std::string, double> accumulated_votes;
if (sequence.empty()) return accumulated_votes;
const std::string& current_word = sequence.back();
for (size_t i = 0; i < sequence.size() - 1; ++i) {
const std::string& prev_word = sequence[i];
auto it1 = transitions.find(prev_word);
if (it1 != transitions.end()) {
auto it2 = it1->second.find(current_word);
if (it2 != it1->second.end()) {
for (const auto& [next_word, vote] : it2->second) {
accumulated_votes[next_word] += vote;
}
}
}
}
return accumulated_votes;
}
/**
* @brief Obtém o vocabulário do modelo.
* @return Referência constante ao conjunto de palavras do vocabulário.
*/
const std::set<std::string>& getVocabulary() const {
return vocabulary;
}
/**
* @brief Exibe as predições ordenadas por peso.
* @param predictions Mapa de palavras candidatas e seus pesos.
* @param sequence Vetor de strings representando a sequência de entrada.
*/
void printPredictions(const std::map<std::string, double>& predictions, const std::vector<std::string>& sequence) const {
std::cout << "Predição (soma de votos normalizados) após sequência terminando com '" << sequence.back() << "':\n";
std::multimap<double, std::string, std::greater<double>> sorted_predictions;
for (const auto& [word, vote] : predictions) {
sorted_predictions.insert({vote, word});
}
if (sorted_predictions.empty()) {
std::cout << " (Nenhuma previsão gerada)\n";
} else {
for (const auto& [vote, word] : sorted_predictions) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(2) << vote << "\n";
}
}
}
};
/**
* @brief Função principal que demonstra o uso da classe PairwiseFeatureAggregator.
*
* Este programa cria um modelo de predição de palavras com base em pares com saltos, treina o modelo
* com cinco sequências do exemplo detalhado, normaliza os pesos, e testa a predição da próxima palavra
* para sequências de teste que demonstram a capacidade do modelo de capturar dependências de longo alcance.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
// Criar o modelo
PairwiseFeatureAggregator model; ///< Instância do modelo de agregação de características.
// Definir sequências de treinamento do exemplo detalhado (5 documentos)
// Nota: O corpus já está pré-processado (minúsculas, sem acentos, sem pontuação).
std::vector<std::string> d1 = {
"verifique", "o", "log", "do", "programa", "e", "descubra", "se", "ele", "foi", "executado", "por", "favor"
};
std::vector<std::string> d2 = {
"verifique", "o", "log", "da", "bateria", "e", "descubra", "se", "ela", "acabou", "por", "favor"
};
std::vector<std::string> d3 = {
"o", "programa", "foi", "executado", "com", "sucesso", "por", "isso", "nao", "precisa", "verificar", "novamente"
};
std::vector<std::string> d4 = {
"a", "bateria", "foi", "substituida", "por", "isso", "esta", "funcionando", "corretamente"
};
std::vector<std::string> d5 = {
"ele", "executou", "o", "programa", "por", "isso", "obteve", "os", "resultados", "esperados"
};
// Adicionar sequências com pesos iguais (20% cada)
double document_weight = 0.2;
model.addSequence(d1, document_weight);
model.addSequence(d2, document_weight);
model.addSequence(d3, document_weight);
model.addSequence(d4, document_weight);
model.addSequence(d5, document_weight);
// Normalizar os pesos
model.normalizeVotes();
// Testar predições para sequência nova (terminando em "executado")
std::vector<std::string> test_sequence1 = {
"verifique", "se", "o", "programa", "foi", "executado"
};
auto predictions1 = model.predictNextWord(test_sequence1);
model.printPredictions(predictions1, test_sequence1);
std::cout << "\n";
// Testar predições para sequência nova com contexto distintivo (terminando em "executado")
std::vector<std::string> test_sequence2 = {
"verifique", "se", "ele", "foi", "executado"
};
auto predictions2 = model.predictNextWord(test_sequence2);
model.printPredictions(predictions2, test_sequence2);
return 0;
}
Considerações importantes
Embora esta abordagem de pares com saltos e votação nos permita considerar contexto de longo alcance, ela enfatiza uma característica negativa. Ao somar votos de muitas características, nossos pares, a contribuição das poucas características realmente informativas (como (programa, executado), no nosso exemplo) pode ser diluída pelo ruído das características menos úteis (como (o, executado)). A diferença entre o total de votos para a palavra correta e as incorretas pode ser pequena, tornando o modelo menos confiável e menos robusto. A esse problema chamamos de diluição do sinal.
Além dessa questão fundamental da diluição do sinal, a abordagem de agregação irrestrita de pares, na prática, enfrenta outros desafios que limitam sua aplicabilidade em cenários mais complexos:
-
Complexidade Computacional e de Memória: a estrutura de dados usada para armazenar as contagens ou votos, como o
std::unordered_maptriplamente aninhado no código C++ (aaargh!), pode se tornar inaceitavelmente grande para corpus com vocabulários extensos. Pior ainda, durante a predição para uma sequência de comprimento $T$, o modelo precisa potencialmente considerar e somar votos de $O(T^2)$ pares $(w_i, w_t)$. Isso torna o método computacionalmente caro e difícil de escalar para as sequências longas frequentemente encontradas em tarefas de Processamento de Linguagem Natural do mundo real. -
Interpretação da Pontuação Final (Normalização): a normalização é realizada individualmente para cada par $(w_i, w_t)\;$, garantindo que $\sum_{w_k} \text{Voto}(w_k \vert w_i, w_t) = 1$. No entanto, a pontuação final para uma palavra candidata $w_k$, calculada como $Score(w_k) = \sum_{i \text{ t.q.} w_i \text{ precede } w_t} \text{Voto}(w_k \vert w_i, w_t)\;$, é uma simples soma dessas probabilidades condicionais. O resultado $Score(w_k)$ não representa mais uma probabilidade bem calibrada; a soma $\sum_{w_k} Score(w_k)$ não é necessariamente $1$. A pontuação final funciona como um ranking: valores mais altos são melhores, mas perde uma interpretação probabilística direta sobre a confiança da previsão.
A forma que encontramos para superar estas dificuldades inclui tentar fazer o modelo prestar atenção dinamicamente nas características, pares ou, mais geralmente, nas palavras anteriores, que são mais relevantes para a previsão atual, mitigando o ruído e controlando a complexidade.
Mascaramento e Atenção Seletiva: Focando no que Importa
A solução para a diluição dos votos é introduzir um mecanismo que permita ao modelo prestar atenção às características mais informativas, ignorando ou diminuindo o peso das demais. Este é um tipo de atenção seletiva. O modelo deve dar mais valor, prestar atenção, as features, características, que contenham mais valor. Parece complicado. Contudo, podemos fazer isso através de uma técnica que chamaremos de mascaramento.
Neste ponto, a criativa leitora deve imaginar que, para a tarefa de prever a palavra após a palavra executado no contexto da frase sobre o programa, precisamos saber, ou de alguma forma aprender, que as características mais importantes são aquelas que envolvem a palavra programa e talvez a palavra foi, enquanto outras como verifique, o, log, etc., serão menos preditivas.
Caso essa informação esteja disponível, podemos criar uma máscara. Essencialmente, essa máscara será um vetor, ou conjunto, de pesos. Neste vetor existe um peso para cada característica. Estas características, ou features, podem ser entendidas como cada palavra anterior que forma um par com a palavra atual. A máscara atribuirá um peso igual a $1$, ou um valor alto, às características ou palavras anteriores que sejam consideradas importantes. Para as demais, atribuirá um peso igual a $0$, ou um valor baixo. Este conceito está representado na Figura 3.
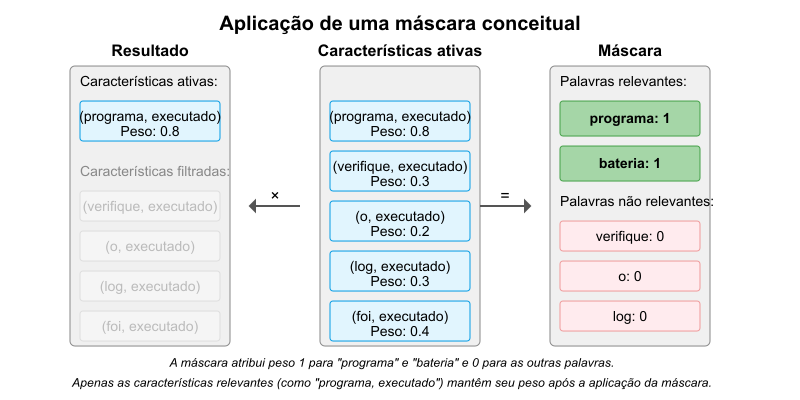 Figura 3: Aplicação de uma máscara conceitual. A máscara (à direita) atribui peso $1$ para “programa” e “bateria” (assumindo que estas são as palavras-chave distintivas) e $0$ para as outras. Ao multiplicar os pesos das características ativas (centro) pela máscara, apenas as características relevantes (“programa, executado” neste caso) mantêm seu peso (resultado à esquerda).
Figura 3: Aplicação de uma máscara conceitual. A máscara (à direita) atribui peso $1$ para “programa” e “bateria” (assumindo que estas são as palavras-chave distintivas) e $0$ para as outras. Ao multiplicar os pesos das características ativas (centro) pela máscara, apenas as características relevantes (“programa, executado” neste caso) mantêm seu peso (resultado à esquerda).
Para aplicar a máscara aos votos que calculamos com o algoritmo da seção anterior (Agregação de Características de Pares), realizamos uma multiplicação elemento a elemento, chamada de produto Hadamard, entre o vetor de votos para cada palavra seguinte possível e a máscara apropriada, ou, de forma equivalente, aplicamos a máscara ao contexto antes de calcular os votos acumulados. qualquer contribuição (o “voto” da nossa analogia anterior) originada de uma característica (par) cujo peso correspondente na máscara seja 0, é zerada.
O Produto de Hadamard
O produto de Hadamard entre duas matrizes $A$ e $B$ de mesmas dimensões, denotado por $A \circ B$ ou $A \odot B$, é uma operação que multiplica os elementos correspondentes das duas matrizes:
\[(A \circ B)_{ij} = A_{ij} \cdot B_{ij}\]Ao contrário da multiplicação matricial padrão, esta operação preserva as dimensões originais e é computacionalmente eficiente. No contexto da atenção seletiva em Transformers, o produto de Hadamard é utilizado para aplicar a máscara ao vetor de características:
\[\text{Características}_{\text{mascaradas}} = \text{Características}_{\text{originais}}\;\; \circ \;\; \text{Máscara}\]Neste caso, a máscara contém valores binários ($0$ ou $1$) ou pesos contínuos entre $0$ e $1$ que determinam a importância relativa de cada elemento. Esta operação permite que o modelo filtre características irrelevantes (multiplicadas por $0$) enquanto mantém as relevantes (multiplicadas por 1, ou por um peso não-nulo).
Com o Produto de Hadamard, a máscara funciona como se estivesse apagando temporariamente as partes menos relevantes da nossa matriz conceitual de votos, deixando apenas as conexões que realmente importam para a decisão atual.
 Figura 4: Matriz de votos/transição conceitual após a aplicação da máscara. Apenas as linhas/características consideradas relevantes (ex: envolvendo “programa” ou “bateria”) permanecem ativas, tornando a previsão mais direcionada.
Figura 4: Matriz de votos/transição conceitual após a aplicação da máscara. Apenas as linhas/características consideradas relevantes (ex: envolvendo “programa” ou “bateria”) permanecem ativas, tornando a previsão mais direcionada.
Aplicando a máscara, os votos das características (pares) consideradas irrelevantes são efetivamente zerados ou reduzidos. Isso faz com que a soma final dos votos seja predominantemente influenciada pelas características importantes, tornando a escolha da palavra seguinte mais clara e confiável..
No exemplo que estamos usando, se a máscara destacar apenas a característica (programa, executado), o total de votos para por virá predominantemente, ou exclusivamente, dessa característica, enquanto os votos para outras palavras serão zerados ou drasticamente reduzidos. Este resultado aumenta a confiança do modelo na previsão da próxima palavra.
Este processo é quase uma forma de focar, prestar atenção, seletivamente às partes específicas do testo, às palavras anteriores mais relevantes, neste caso, para tomar uma decisão sobre a próxima palavra. Este é o conceito que suporta o mecanismo de ATENÇÃO.
O artigo seminal Attention is All You Need (Vaswani et al., 2017) introduziu uma forma específica e poderosa de implementar essa ideia, que se tornou a base dos modelos Transformer.
A origem do termo Transformer está ligada à capacidade do modelo de transformar representações de sequências (como texto) por meio de mecanismos de autoatenção (self-attention), sem depender de redes neurais recorrentes (RNNs) ou convolucionais (CNNs).
A persistente leitora deve ter percebido que até agora, tudo que fizemos foi uma aproximação conceitual para construir as estruturas cognitivas do entendimento. Isso não basta. Assim como fizemos anteriormente, vamos recorrer a um exemplo mais rigoroso, com um pouco de matemática, em um cenário um pouco mais complexo, ainda que distante da realidade.
Exemplo Detalhado: Mascaramento em Corpus Realista
Consideremos um vocabulário definido por $V = {w_1, w_2, …, w_{ \vert V \vert }}$ e uma sequência $S = [w_5, w_{17}, w_3, w_{42}, w_{11}]$. Vamos focar na posição atual $t=4$ (palavra $w_{11}$) e considerar todas as posições anteriores $i \in {0, 1, 2, 3}$.
Para entender o mecanismo de atenção, vamos analisar $6$ passos importantes:
-
Representação vetorial (embeddings)
Em processamento de linguagem natural, um embedding é uma representação vetorial de palavras, frases ou outros elementos linguísticos em um espaço contínuo de baixa dimensão. É uma técnica fundamental que permite converter palavras, elementos discretos, em vetores numéricos $\vec{w} \in \mathbb{R}^d$ que capturem suas propriedades semânticas e relações com outras palavras.
As principais características dos embeddings são:
-
Representação densa em vetor: cada palavra $w$ é mapeada para um vetor $\vec{w} = [w_1, w_2, …, w_d]$ de números reais, tipicamente com dimensões entre $50 \leq d \leq 300$ elementos, em vez de um vetor one-hot esparso com milhares ou milhões de dimensões.
-
Preservação de similaridade semântica: palavras com significados semelhantes ficam próximas no espaço vetorial. A similaridade é frequentemente medida usando a similaridade de cosseno, dada por:
\[\text{sim}(\vec{w}_i, \vec{w}_j) = \frac{\vec{w}_i \cdot \vec{w}_j}{ \vert \vec{w}_i \vert \cdot \vert \vec{w}_j \vert }\] -
Captura de relações analógicas: embeddings resultantes de um bom treinamento podem capturar relações como “rei está para rainha assim como homem está para mulher” através de operações vetoriais simples, como:
\[\vec{v}_{\text{rei} } - \vec{v}_{\text{homem} } + \vec{v}_{\text{mulher} } \approx \vec{v}_{\text{rainha} }\] -
Aprendizado por contexto: os embeddings são geralmente aprendidos em um treinamento baseado na observação de como as palavras aparecem em contextos semelhantes usando grandes corpus de texto, otimizando uma função objetivo como:
Neste caso, $c$ é o tamanho da janela de contexto e $p(w_{t+j} \vert w_t)$ é a probabilidade de observar a palavra $w_{t+j}$ dado $w_t$.
Alguns modelos populares de word embeddings incluem:
- Word2Vec: desenvolvido pelo Google em 2013, usando redes neurais para prever palavras vizinhas (skipgram) ou a palavra atual a partir das vizinhas (CBOW). A esforçada leitora deveria ler este artigo antes de continuar.
- GloVe: desenvolvido por Stanford, combinando estatísticas globais de co-ocorrência $X_{ij}$ com aprendizado local de contexto, dado por:
FastText: desenvolvido pelo Facebook, considera subpalavras (N-grams de caracteres) para lidar melhor com palavras raras e morfologia:
\[\vec{w} = \frac{1}{ \vert G_w \vert } \sum_{g \in G_w} \vec{z}_g\]No FastText, $G_w$ é o conjunto de N-grams na palavra $w$ e $\vec{z}_g$ é o vetor do N-gram $g$.
Em modelos como os Transformers, os embeddings são apenas o primeiro passo. Cada token, palavra ou subpalavra, será primeiro convertido em um vetor de embedding e depois processado através das camadas de atenção e feed-forward para produzir representações contextualizadas $\mathbf{h}_i^l$ que capturam o significado da palavra no contexto específico em que aparece:
\[\mathbf{h}_i^l = \text{TransformerLayer}_l\;(\mathbf{h}_i^{l-1}, mathbf{h}_{\neq i}^{l-1})\]na qual, $\mathbf{h}_i^0 = \text{Embedding}(w_i) + \text{PositionalEncoding}(i)$
Voltando ao nosso exemplo, cada palavra será representada por um vetor de embedding $\mathbf{e}_i \in \mathbb{R}^d$. Neste caso, $d$ é a dimensão do embedding. Vamos assumir $d=4$ para manter a simplicidade. Se considerarmos alguns valores hipotéticos para os embeddings de palavras, poderíamos ter:
\[\mathbf{e}_0 = \mathbf{e}_{w_5} = [0.2, -0.3, 0.1, 0.5]\] \[\mathbf{e}_1 = \mathbf{e}_{w_{17}} = [0.4, 0.1, -0.2, 0.3]\] \[\mathbf{e}_2 = \mathbf{e}_{w_3} = [-0.1, 0.5, 0.3, 0.2]\] \[\mathbf{e}_3 = \mathbf{e}_{w_{42}} = [0.6, 0.2, -0.4, 0.1]\] \[\mathbf{e}_4 = \mathbf{e}_{w_{11}} = [0.3, 0.4, 0.2, -0.1]\] -
-
Cálculo de Query, Key, Value:
A conversão de embeddings em vetores Query, Key e Value por meio de transformações lineares é uma parte importante do mecanismo de atenção. Essas transformações irão permitir que o modelo aprenda a focar em diferentes partes do texto de entrada, dependendo do contexto e da tarefa. Notadamente porque os embeddings originais $\mathbf{X} \in \mathbb{R}^{n \times d}$ representam palavras em um espaço semântico geral. As transformações lineares permitem projetar esses embeddings em subespaços especializados:
\[\mathbf{Q} = \mathbf{X}\mathbf{W}^Q, \quad \mathbf{K} = \mathbf{X}\mathbf{W}^K, \quad \mathbf{V} = \mathbf{X}\mathbf{W}^V\]Nessas transformações, $\mathbf{W}^Q, \mathbf{W}^K,$ e $\mathbf{W}^V$ são as matrizes de pesos utilizadas. Elas pertencem ao espaço $\mathbb{R}^{d \times d_k}\;$ e seus elementos são os parâmetros ajustados, aprendidos, durante o treinamento do modelo.
Cada projeção serve a um propósito específico:
-
$\mathbf{Q}$ (Query): codifica como uma palavra “busca” informações relevantes;
-
$\mathbf{K}$ (Key): determina como uma palavra “responde” a buscas;
-
$\mathbf{V}$ (Value): contém a informação semântica efetiva a ser propagada.
Sem estas transformações, o mecanismo de atenção seria limitado à equação:
\[\text{Attention}(\mathbf{X}, \mathbf{X}, \mathbf{X}) = \text{softmax}\left(\frac{\mathbf{X}\mathbf{X}^T}{\sqrt{d} }\right)\mathbf{X}\]O uso de parâmetros separados $\mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V$ aumenta significativamente os graus de liberdade do modelo:
\[\text{Attention}(\mathbf{X}\mathbf{W}^Q, \mathbf{X}\mathbf{W}^K, \mathbf{X}\mathbf{W}^V) = \text{softmax}\left(\frac{\mathbf{X}\mathbf{W}^Q(\mathbf{X}\mathbf{W}^K)^T}{\sqrt{d_k} }\right)\mathbf{X}\mathbf{W}^V\]As matrizes $\mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V$ são os parâmetros aprendidos durante o treinamento, permitindo que o modelo se adapte dinamicamente em relação às características mais relevantes para a tarefa em questão. O modelo aprende:
- Quais aspectos dos embeddings são importantes para consultas;
- Quais aspectos tornam um token consultável por outros;
- Quais informações devem ser transmitidas quando um token é consultado.
Além disso, as transformações lineares permitem mapear embeddings de dimensão $d$ para vetores $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ de dimensão $d_k$, potencialmente diferente de $d$. Isso é útil para reduzir a complexidade computacional, especialmente em tarefas de atenção multi-cabeça. Neste caso, cada cabeça pode ter uma dimensão diferente:
\[\mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V \in \mathbb{R}^{d \times d_k}\]Isso possibilita controlar a complexidade computacional e a capacidade representacional do mecanismo de atenção.
O termo cabeça (head) se refere a uma instância completa do mecanismo de atenção, scaled dot-product attention, rodando independente ou em paralelo com outras instâncias.
Voltando ao nosso exemplo: usamos transformações lineares para converter embeddings nos vetores Query, Key e Value:
\[\mathbf{Q} = \mathbf{E}\mathbf{W}^Q, \quad \mathbf{K} = \mathbf{E}\mathbf{W}^K, \quad \mathbf{V} = \mathbf{E}\mathbf{W}^V\]Sendo assim, $\mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V \in \mathbb{R}^{d \times d_k}$ são matrizes de parâmetros aprendidas. Assumiremos $d_k = 3$ e matrizes simplificadas dadas por:
\[\mathbf{W}^Q = \begin{bmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.1 \\ 0.2 & 0.3 & 0.4 \\ 0.5 & 0.1 & 0.2 \end{bmatrix}, \mathbf{W}^K = \begin{bmatrix} 0.3 & 0.2 & 0.1 \\ 0.1 & 0.4 & 0.3 \\ 0.5 & 0.2 & 0.3 \\ 0.2 & 0.1 & 0.5 \end{bmatrix}, \mathbf{W}^V = \begin{bmatrix} 0.2 & 0.3 & 0.1 \\ 0.4 & 0.2 & 0.3 \\ 0.1 & 0.5 & 0.2 \\ 0.3 & 0.1 & 0.4 \end{bmatrix}\]Calculando $\mathbf{q}_4$ (Query para posição atual), $\mathbf{k}_i$ (Key para cada posição) e $\mathbf{v}_i$ (Value para cada posição), teremos:
\[\mathbf{q}_4 = \mathbf{e}_4\mathbf{W}^Q = [0.3, 0.4, 0.2, -0.1] \begin{bmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.1 \\ 0.2 & 0.3 & 0.4 \\ 0.5 & 0.1 & 0.2 \end{bmatrix} = [0.23, 0.31, 0.21]\]De modo similar, calculamos $\mathbf{k}_i$ para $i \in {0, 1, 2, 3, 4}$ e $\mathbf{v}_i$ para $i \in {0, 1, 2, 3, 4}$.
-
-
Cálculo dos scores de atenção (sem mascaramento):
Os scores de atenção, similaridade entre $\mathbf{q}_4$ e cada $\mathbf{k}_i$ são:
\[s_{4,i} = \frac{\mathbf{q}_4 \cdot \mathbf{k}_i}{\sqrt{d_k}}\]Por exemplo:
\[s_{4,0} = \frac{[0.23, 0.31, 0.21] \cdot [0.23, 0.05, 0.22]}{\sqrt{3}} = \frac{0.1262}{\sqrt{3}} = 0.0729\]Similarmente, calculamos $s_{4,1} = 0.1039$, $s_{4,2} = 0.1501$, $s_{4,3} = 0.0592$ e $s_{4,4} = 0.1327$
-
Aplicação de mascaramento explícito:
A ideia do mascaramento é zerar scores de posições não relevantes. Vamos considerar que apenas as posições 0 e 2 são relevantes para a posição atual. Criamos uma máscara $\mathbf{M}$:
\[\mathbf{M}_4 = [1, 0, 1, 0, 1]\]Aplicamos a máscara aos scores:
\[\tilde{s}_{4,i} = s_{4,i} \cdot \mathbf{M}_{4,i}\]Resultando em:
\[\tilde{s}_{4,0} = 0.0729 \cdot 1 = 0.0729\] \[\tilde{s}_{4,1} = 0.1039 \cdot 0 = 0\] \[\tilde{s}_{4,2} = 0.1501 \cdot 1 = 0.1501\] \[\tilde{s}_{4,3} = 0.0592 \cdot 0 = 0\] \[\tilde{s}_{4,4} = 0.1327 \cdot 1 = 0.1327\] -
Normalização via softmax:
A função softmax é uma transformação matemática fundamental em aprendizado de máquina, especialmente em redes neurais e modelos de linguagem. Ela converte um vetor de números reais em uma distribuição de probabilidade.
Para um vetor $\mathbf{z} = [z_1, z_2, \ldots, z_n]$, a função softmax é definida como:
\[\text{softmax}(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}}\]Esta função tem propriedades importantes:
-
Normalização: os valores resultantes somam $1$, permitindo sua interpretação como probabilidades:
\[\sum_{i=1}^{n} \text{softmax}(\mathbf{z})_i = 1\] -
Diferenciabilidade: a função é suave e tem derivadas bem definidas em todos os pontos, facilitando o treinamento por gradiente descendente:
\[\frac{\partial \text{softmax}(\mathbf{z})_i}{\partial z_j} = \begin{cases} \text{softmax}(\mathbf{z})_i(1-\text{softmax}(\mathbf{z})_i) & \text{se } i = j \\ -\text{softmax}(\mathbf{z})_i\text{softmax}(\mathbf{z})_j & \text{se } i \neq j \end{cases}\]-
Não-linearidade: Transforma relações lineares em não-lineares, permitindo que redes neurais aprendam mapeamentos complexos.
-
Amplificação: Enfatiza valores maiores e suprime menores. Se $z_i \gg z_j$, então $\text{softmax}(\mathbf{z})_i \gg \text{softmax}(\mathbf{z})_j$.
-
-
Escala invariante: Adicionar uma constante $c$ a todos os elementos não altera o resultado:
\[\text{softmax}([z_1+c, z_2+c, \ldots, z_n+c])_i = \text{softmax}([z_1, z_2, \ldots, z_n])_i\]Esta propriedade é frequentemente explorada para estabilidade numérica:
\[\text{softmax}(\mathbf{z})_i = \frac{e^{z_i-\max(\mathbf{z})} }{\sum_{j=1}^{n} e^{z_j-\max(\mathbf{z})} }\]
No contexto do mecanismo de atenção em Transformers, a função softmax normaliza os scores de atenção em pesos que somam $1$:
\[\alpha_{ij} = \frac{\exp(s_{ij})}{\sum_{k=1}^{n} \exp(s_{ik})}\]Na qual, $s_{ij}$ é o score de similaridade entre as posições $i$ e $j$.
No nosso exemplo os pesos de atenção normalizados são obtidos aplicando softmax aos scores mascarados:
\[\alpha_{4,i} = \frac{\exp(\tilde{s}_{4,i})}{\sum_{j=0}^{4} \exp(\tilde{s}_{4,j})}\]Calculando:
\[\alpha_{4,0} = \frac{\exp(0.0729)}{\exp(0.0729) + \exp(0) + \exp(0.1501) + \exp(0) + \exp(0.1327)}\] \[\alpha_{4,0} = \frac{1.0756}{1.0756 + 1 + 1.1620 + 1 + 1.1419} = 0.2518\]Similarmente:
\[\alpha_{4,1} = 0.2341\] \[\alpha_{4,2} = 0.2720\] \[\alpha_{4,3} = 0.2341\] \[\alpha_{4,4} = 0.2674\] -
-
Combinação ponderada dos Values:
Finalmente, o vetor de contexto para a posição $4$ é:
\[\mathbf{c}_4 = \sum_{i=0}^{4} \alpha_{4,i} \mathbf{v}_i\] \[\mathbf{c}_4 = 0.2518 \cdot \mathbf{v}_0 + 0 \cdot \mathbf{v}_1 + 0.2720 \cdot \mathbf{v}_2 + 0 \cdot \mathbf{v}_3 + 0.2674 \cdot \mathbf{v}_4\]Este vetor de contexto $\mathbf{c}_4$ agora contém informações das posições relevantes $(0, 2, 4)$, com as posições não relevantes $(1, 3)$ efetivamente excluídas pelo mascaramento.
Exemplo de Implementação: Agregação de Características de Pares com C++
Vejamos como o mascaramento pode ser implementado em C++, aplicando a máscara antes de acumular os votos (demonstração conceitual):
#include <iostream> ///< Para entrada e saída padrão (std::cout).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de sequências.
#include <string> ///< Para std::string, usado em palavras e mensagens.
#include <unordered_map> ///< Para std::unordered_map, usado no armazenamento de transições.
#include <map> ///< Para std::map, usado na ordenação de predições.
#include <set> ///< Para std::set, usado no armazenamento do vocabulário.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
/**
* @class PairwiseFeatureAggregator
* @brief Uma classe para modelar transições de palavras com base em pares com saltos.
*
* Esta classe implementa um modelo que associa pares de palavras (anterior, atual) a palavras seguintes,
* acumulando pesos (votos) para prever a próxima palavra em uma sequência. Os pesos são normalizados
* para cada par (anterior, atual) como probabilidades condicionais.
*/
class PairwiseFeatureAggregator {
private:
std::unordered_map<std::string,
std::unordered_map<std::string,
std::unordered_map<std::string, double>>> transitions; ///< Estrutura para armazenar transições: transitions[palavra_anterior][palavra_atual][proxima_palavra] -> peso.
std::set<std::string> vocabulary; ///< Vocabulário global de palavras.
public:
/**
* @brief Adiciona uma sequência ao modelo, acumulando pesos para transições.
* @param sequence Vetor de strings representando a sequência de palavras.
* @param weight Peso a ser atribuído à sequência (padrão é 1.0).
*/
void addSequence(const std::vector<std::string>& sequence, double weight = 1.0) {
if (sequence.size() < 3) return; // Necessário pelo menos (anterior, atual, próxima)
// Adicionar palavras ao vocabulário
for (const auto& word : sequence) {
vocabulary.insert(word);
}
// Para cada posição atual, associar pares (anterior, atual) à próxima palavra
for (size_t current_pos = 1; current_pos < sequence.size() - 1; ++current_pos) {
const std::string& current_word = sequence[current_pos];
const std::string& next_word = sequence[current_pos + 1];
for (size_t prev_pos = 0; prev_pos < current_pos; ++prev_pos) {
const std::string& prev_word = sequence[prev_pos];
transitions[prev_word][current_word][next_word] += weight;
}
}
}
/**
* @brief Normaliza os pesos (votos) para cada par (anterior, atual) como probabilidades.
*/
void normalizeVotes() {
for (auto& [prev_word, inner_map1] : transitions) {
for (auto& [current_word, inner_map2] : inner_map1) {
double total_votes = 0.0;
for (auto const& [next_word, vote] : inner_map2) {
total_votes += vote;
}
if (total_votes > 0) {
for (auto& [next_word, vote] : inner_map2) {
inner_map2[next_word] /= total_votes;
}
}
}
}
}
/**
* @brief Prediz a próxima palavra com base na sequência fornecida.
* @param sequence Vetor de strings representando a sequência de entrada.
* @return Mapa ordenado de palavras candidatas para a próxima palavra e seus pesos acumulados.
*/
std::map<std::string, double> predictNextWord(const std::vector<std::string>& sequence) const {
std::map<std::string, double> accumulated_votes;
if (sequence.empty()) return accumulated_votes;
const std::string& current_word = sequence.back();
for (size_t i = 0; i < sequence.size() - 1; ++i) {
const std::string& prev_word = sequence[i];
auto it1 = transitions.find(prev_word);
if (it1 != transitions.end()) {
auto it2 = it1->second.find(current_word);
if (it2 != it1->second.end()) {
for (const auto& [next_word, vote] : it2->second) {
accumulated_votes[next_word] += vote;
}
}
}
}
return accumulated_votes;
}
/**
* @brief Obtém o vocabulário do modelo.
* @return Referência constante ao conjunto de palavras do vocabulário.
*/
const std::set<std::string>& getVocabulary() const {
return vocabulary;
}
/**
* @brief Exibe as predições ordenadas por peso.
* @param predictions Mapa de palavras candidatas e seus pesos.
* @param sequence Vetor de strings representando a sequência de entrada.
*/
void printPredictions(const std::map<std::string, double>& predictions, const std::vector<std::string>& sequence) const {
std::cout << "Predição (soma de votos normalizados) após sequência terminando com '" << sequence.back() << "':\n";
std::multimap<double, std::string, std::greater<double>> sorted_predictions;
for (const auto& [word, vote] : predictions) {
sorted_predictions.insert({vote, word});
}
if (sorted_predictions.empty()) {
std::cout << " (Nenhuma previsão gerada)\n";
} else {
for (const auto& [vote, word] : sorted_predictions) {
std::cout << " " << word << ": " << std::fixed << std::setprecision(2) << vote << "\n";
}
}
}
};
/**
* @brief Função principal que demonstra o uso da classe PairwiseFeatureAggregator.
*
* Este programa cria um modelo de predição de palavras com base em pares com saltos, treina o modelo
* com um conjunto de sequências (o exemplo detalhado com cinco documentos é usado por padrão), normaliza
* os pesos, e testa a predição da próxima palavra para uma sequência de teste. O exemplo simples com
* dois documentos está incluído, mas comentado.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
// Exemplo detalhado com cinco documentos
std::cout << "--- Exemplo Detalhado (5 Documentos) ---\n";
PairwiseFeatureAggregator model_detailed; ///< Instância do modelo para o exemplo detalhado.
// Definir sequências de treinamento (exemplo detalhado)
// Nota: O corpus já está pré-processado (minúsculas, sem acentos, sem pontuação).
std::vector<std::string> detailed_d1 = {
"verifique", "o", "log", "do", "programa", "e", "descubra", "se", "ele", "foi", "executado", "por", "favor"
};
std::vector<std::string> detailed_d2 = {
"verifique", "o", "log", "da", "bateria", "e", "descubra", "se", "ela", "acabou", "por", "favor"
};
std::vector<std::string> detailed_d3 = {
"o", "programa", "foi", "executado", "com", "sucesso", "por", "isso", "nao", "precisa", "verificar", "novamente"
};
std::vector<std::string> detailed_d4 = {
"a", "bateria", "foi", "substituida", "por", "isso", "esta", "funcionando", "corretamente"
};
std::vector<std::string> detailed_d5 = {
"ele", "executou", "o", "programa", "por", "isso", "obteve", "os", "resultados", "esperados"
};
// Adicionar sequências com pesos iguais (20% cada)
double detailed_weight = 0.2;
model_detailed.addSequence(detailed_d1, detailed_weight);
model_detailed.addSequence(detailed_d2, detailed_weight);
model_detailed.addSequence(detailed_d3, detailed_weight);
model_detailed.addSequence(detailed_d4, detailed_weight);
model_detailed.addSequence(detailed_d5, detailed_weight);
// Normalizar os pesos
model_detailed.normalizeVotes();
// Testar predições para sequência de teste
std::vector<std::string> test_detailed_1 = {
"verifique", "se", "o", "programa", "foi", "executado"
};
auto predictions_detailed_1 = model_detailed.predictNextWord(test_detailed_1);
model_detailed.printPredictions(predictions_detailed_1, test_detailed_1);
std::cout << "\n";
// Exemplo simples com dois documentos (comentado)
/*
std::cout << "--- Exemplo Simples (2 Documentos) ---\n";
PairwiseFeatureAggregator model_simple; ///< Instância do modelo para o exemplo simples.
std::vector<std::string> sequence1 = {
"verifique", "o", "log", "do", "programa", "e", "descubra", "se", "ele", "foi", "executado", "por", "favor"
};
std::vector<std::string> sequence2 = {
"verifique", "o", "log", "da", "bateria", "e", "descubra", "se", "ela", "acabou", "por", "favor"
};
model_simple.addSequence(sequence1, 0.5);
model_simple.addSequence(sequence2, 0.5);
model_simple.normalizeVotes();
std::vector<std::string> test_sequence1 = {
"verifique", "o", "log", "do", "programa", "e", "descubra", "se", "ele", "foi", "executado"
};
auto predictions1 = model_simple.predictNextWord(test_sequence1);
model_simple.printPredictions(predictions1, test_sequence1);
std::vector<std::string> test_sequence2 = {
"verifique", "o", "log", "da", "bateria", "e", "descubra", "se", "ela", "acabou"
};
auto predictions2 = model_simple.predictNextWord(test_sequence2);
model_simple.printPredictions(predictions2, test_sequence2);
std::cout << "\n";
*/
return 0;
}
A implementação em C++ 20 ilustra como o mascaramento pode ser aplicado para focar apenas nas palavras relevantes, permitindo que o modelo faça previsões mais precisas. O código é modular e pode ser facilmente adaptado para diferentes sequências e máscaras.
A atenta leitora já deve ter entendido a necessidade do mecanismo de atenção e a intuição que suporta esta ideia: focar seletivamente no que é relevante usando mascaramento/ponderação. A próxima pergunta que a curiosa leitora precisa fazer é:
como esse processo de seleção e ponderação é implementado de forma eficiente e, ainda mais importante, aprendido pelos modelos?
Nesta altura da nossa jornada despontam no horizonte as operações matriciais que definem a atenção nos Transformers.
Atenção como Multiplicação de Matrizes: Aprendendo a Focar
Vou considerar que esperta leitora já entendeu a intuição da atenção como um mecanismo de foco seletivo, usando mascaramento ou ponderação para destacar informações relevantes. Nos resta encontrar uma forma de implementar essa tecnologia de forma eficiente permitindo ao modelo aprender quais informações são relevantes em cada contexto. Isso quer dizer que: para ser eficiente, a máscara não pode ser fixa. Isso quer dizer que a máscara precisa ser criada de acordo com o contexto atual da palavra para a qual estamos tentando prever a próxima palavra e com o contexto das palavras que vieram antes.
Este mecanismo que vamos descrever, onde cada palavra em uma sequência presta atenção a todas as outras palavras da mesma sequência, incluindo a si mesma, é conhecido como auto-atenção (self-attention). É auto porque a mesma sequência serve tanto como fonte de consulta quanto como fonte de informação a ser consultada.
Para que seja possível que os modelos possam aprender esses padrões de atenção e para que o cálculo seja eficiente em hardware moderno, como GPUs e TPUs, buscaremos expressar todo o processo através de operações de matrizes diferenciáveis. Isso permite que usemos algoritmos como os algoritmos de retropropagação (backpropagation) para ajustar os pesos do modelo.
Operações de Matrizes Diferenciáveis
As operações de matrizes diferenciáveis, que estudamos aqui, referem-se a funções que mapeiam matrizes para matrizes, ou para escalares, mantendo propriedades de diferenciabilidade. Essas operações são fundamentais em problemas de otimização, particularmente em aprendizado profundo e matemática computacional.
\[\lim_{H \rightarrow 0} \frac{f(X + H) - f(X) - \langle \nabla f(X), H \rangle_F}{\|H\|_F} = 0\]Seja $f: \mathbb{R}^{m \times n} \rightarrow \mathbb{R}$ uma função que mapeia uma matriz $X \in \mathbb{R}^{m \times n}$ para um escalar. Esta função é diferenciável em $X$ se existe uma matriz $\nabla f(X) \in \mathbb{R}^{m \times n}$ tal que:
Neste caso, $\langle A, B \rangle_F = \text{tr}(A^T B)$ é o produto escalar estendido para matrizes e $|H|_F$ é a norma de Euclidiana de Matrizes.
Entre as Operações de Matrizes Diferenciáveis podemos destacar:
- Adição de Matrizes: $f(A, B) = A + B$
- Derivada: $\frac{\partial f}{\partial A} = I$, $\frac{\partial f}{\partial B} = I$
- Multiplicação de Matrizes: $f(A, B) = AB$
- Derivada: $\frac{\partial f}{\partial A} = B^T$, $\frac{\partial f}{\partial B} = A^T$
- Traço de Matriz: $f(A) = \text{tr}(A)$
- Derivada: $\frac{\partial f}{\partial A} = I$
- Determinante de Matriz: $f(A) = \det(A)$
- Derivada: $\frac{\partial f}{\partial A} = \det(A) \cdot (A^{-1})^T$
- Inversa de Matriz: $f(A) = A^{-1}$
- Derivada: $\frac{\partial f}{\partial A_{ij}} = -(A^{-1}){ik}(A^{-1}){lj}$
Estas operações são essenciais em algoritmos de otimização, especialmente em aprendizado profundo, onde a retropropagação é usada para calcular gradientes e atualizar pesos de modelos. Elas permitem que os modelos aprendam a partir de dados, ajustando seus parâmetros para minimizar funções de perda.
| A abordagem de Agregação de Características de Pares, detalhada anteriormente, pode ser vista como uma forma de consulta implícita. Para cada palavra atual $w_t$, o modelo consulta uma vasta coleção de informações pré-calculadas (os votos $\text{Voto}(w_k | w_i, w_t)$) associadas a cada par possível $(w_i, w_t)$ formado com palavras anteriores $w_i$. Esse conjunto de votos armazenados age como uma tabela de consulta distribuída, onde a chave de busca será o par específico $(w_i, w_t)$ e o valor será a distribuição de votos sobre as palavras seguintes $w_k$. A introdução do mascaramento na seção anterior representa um passo para tornar essa consulta mais seletiva, focando apenas nas entradas da tabela (pares) consideradas mais relevantes para o contexto atual. |
O processo geralmente envolve três componentes principais, derivados da representação vetorial, embedding, de cada palavra na sequência:
- Query (Consulta - Q): um vetor que representa a palavra/posição atual, atuando como uma “sonda” para buscar informações relevantes.
- Key (Chave - K): um vetor associado a cada palavra na sequência (incluindo as anteriores), que pode ser “comparado” com a Query para determinar a relevância.
- Value (Valor - V): um vetor associado a cada palavra na sequência, contendo a informação que será efetivamente passada adiante se a palavra for considerada relevante.
A relevância entre uma Query (palavra atual $t$) e uma Key (palavra anterior $i$) é calculada medindo a similaridade entre $Q_t$ e $K_i$. Uma forma comum e eficiente de fazer isso é através do produto escalar (dot product) que vimos aqui. Porém, podemos calcular todos os scores de similaridade para a palavra $t$ em relação a todas as palavras anteriores $i$ (e a própria $t$) de uma vez só usando multiplicação de matrizes:
\[\text{Scores}_t = Q_t \cdot K^T\]Neste caso, $Q_t$ é o vetor query da palavra $t$, e $K$ é uma matriz na qual cada linha $K_i$ é o vetor chave da palavra $i$. O resultado $\text{Scores}_t$ é um vetor no qual cada elemento $j$ representa a similaridade bruta entre a query $t$ e a chave $j$.
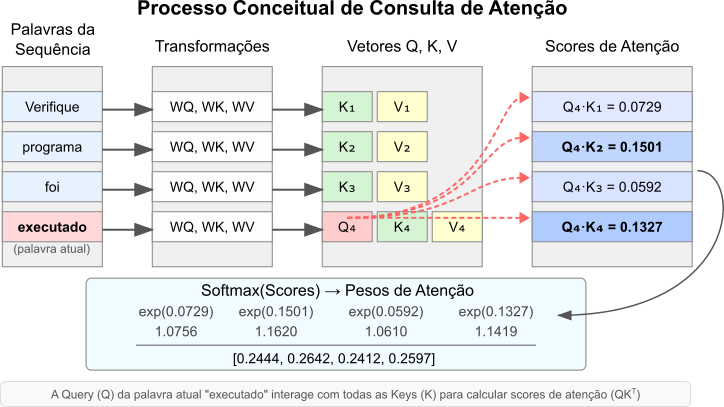 Figura 5: Processo conceitual de consulta de atenção. A Query (Q) da palavra atual interage com as Keys (K) das palavras anteriores (e da atual) para gerar scores de atenção. (Nota: A figura original ilustrava uma busca de máscara; aqui reinterpretamos como cálculo de scores QK^T).
Figura 5: Processo conceitual de consulta de atenção. A Query (Q) da palavra atual interage com as Keys (K) das palavras anteriores (e da atual) para gerar scores de atenção. (Nota: A figura original ilustrava uma busca de máscara; aqui reinterpretamos como cálculo de scores QK^T).
Esses scores brutos precisam ser normalizados para se tornarem pesos de atenção que somam $1$. Isso é feito aplicando a função softmax. Além disso, no artigo original do Transformer, os scores são escalonados por $\sqrt{d_k}$ (aqui $d_k$ é a dimensão dos vetores Key/Query) antes do softmax para estabilizar os gradientes durante o treinamento:
\[\text{AttentionWeights}_t = \text{softmax}\left( \frac{Q_t \cdot K^T}{\sqrt{d_k}} \right)\]O resultado $\text{AttentionWeights}t$ é um vetor de pesos. Neste caso, cada peso $\alpha{ti}$ indica quanta atenção a palavra $t$ deve prestar à palavra $i$.
Finalmente, o vetor de contexto para a palavra $t$, $C_t$, é calculado como uma soma ponderada dos vetores Value ($V$) de todas as palavras, usando os pesos de atenção calculados:
\[C_t = \sum_{i} \alpha_{ti} V_i\]Este processo inteiro pode ser expresso de forma compacta para todas as palavras de uma sequência simultaneamente usando matrizes $Q$, $K$, $V$, aqui, cada linha representa uma palavra:
\[\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{QK^T}{\sqrt{d_k}} \right) V\]Esta formulação específica é conhecida como Scaled Dot-Product Attention e foi a principal proposta do influente artigo “Attention Is All You Need” (Vaswani et al., 2017). Quando essa operação de atenção é aplicada dentro da mesma sequência, ou seja, as matrizes Q, K e V são derivadas da mesma sequência de entrada chamamos este processo de auto-atenção (self-attention). Este é precisamente o mecanismo central dos Transformers.
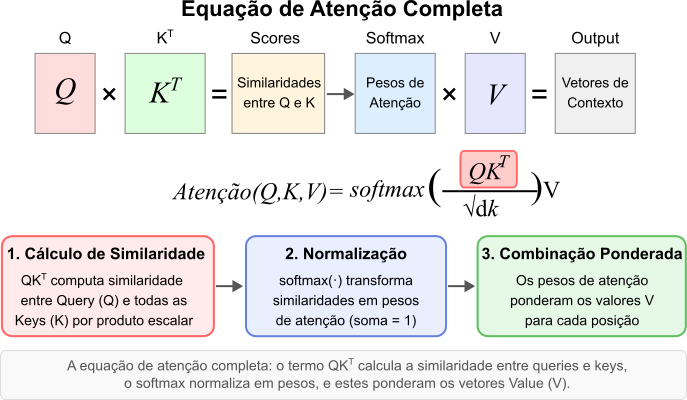 Figura 6: A equação de atenção completa. O termo $QK^T$ calcula a similaridade, o softmax normaliza em pesos, e estes ponderam os vetores Value (V).
Figura 6: A equação de atenção completa. O termo $QK^T$ calcula a similaridade, o softmax normaliza em pesos, e estes ponderam os vetores Value (V).
É importante que a persistente leitora note que as matrizes $Q$, $K$, e $V$ não correspondem diretamente aos embeddings originais das palavras. Elas são, na verdade, o resultado de transformações lineares aplicadas aos embeddings de entrada. Essas transformações são definidas por matrizes de pesos ($W_Q, W_K, W_V$) cujos valores são aprendidos, ou se preferir: ajustados, durante o processo de treinamento do modelo. Isso concede ao modelo a flexibilidade para aprender quais aspectos das palavras são relevantes para atuar como query, key ou value em diferentes contextos.
Este mecanismo de atenção robusto e flexível é uma das principais inovações dos Transformers. Ele permite que o modelo:
- Capture dependências de longo alcance entre palavras, mesmo em sequências longas;
- Atenue a influência de palavras irrelevantes, focando apenas nas mais relevantes para a tarefa em questão;
- Ajuste dinamicamente a atenção com base no contexto, aprendendo quais palavras são mais relevantes em cada situação;
- Permita que o modelo aprenda a importância relativa de diferentes palavras, sem depender de uma estrutura fixa ou pré-definida.
Além disso, o mesmo mecanismo de atenção pode ser aplicado a diferentes partes da sequência, simultaneamente e em paralelo, permitindo que o modelo aprenda a focar em diferentes aspectos do contexto em diferentes momentos. Isso é especialmente útil em tarefas como tradução automática, onde o significado de uma palavra pode depender fortemente do contexto em que aparece.
Exemplo numérico: Atenção com Máscara
Para ilustrar como funciona o mecanismo de atenção na prática, vamos trabalhar com um exemplo numérico simplificado. Neste exemplo vamos considerar uma sequência de $3$ palavras. Nesta sequência cada palavra está representada por um embedding de dimensão $d=4$.
-
Embeddings Iniciais: suponha que temos os seguintes embeddings para nossa sequência:
\[\mathbf{x}_1 = [0.2, -0.1, 0.5, 0.3] \quad \text{(primeira palavra)}\] \[\mathbf{x}_2 = [0.5, 0.2, -0.3, 0.1] \quad \text{(segunda palavra)}\] \[\mathbf{x}_3 = [-0.1, 0.4, 0.2, 0.6] \quad \text{(terceira palavra)}\]Podemos organizar esses vetores em uma matriz de entrada $\mathbf{X} \in \mathbb{R}^{3 \times 4}$:
\[\mathbf{X} = \begin{bmatrix} 0.2 & -0.1 & 0.5 & 0.3 \\ 0.5 & 0.2 & -0.3 & 0.1 \\ -0.1 & 0.4 & 0.2 & 0.6 \end{bmatrix}\] -
Transformações Lineares para Q, K, V: aplicamos transformações lineares para obter as matrizes Query ($\mathbf{Q}$), Key ($\mathbf{K}$) e Value ($\mathbf{V}$). Vamos assumir matrizes de peso $\mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V \in \mathbb{R}^{4 \times 3}$ (transformando de dimensão $d=4$ para dimensão $d_k=3$), idênticas às do exemplo original para manter a comparação:
\[\mathbf{W}^Q = \begin{bmatrix} 0.1 & 0.4 & 0.2 \\ 0.3 & -0.2 & 0.5 \\ 0.6 & 0.1 & -0.3 \\ -0.1 & 0.3 & 0.4 \end{bmatrix} \quad \mathbf{W}^K = \begin{bmatrix} 0.2 & 0.1 & 0.3 \\ 0.5 & -0.3 & 0.2 \\ -0.1 & 0.4 & 0.2 \\ 0.3 & 0.2 & -0.1 \end{bmatrix} \quad \mathbf{W}^V = \begin{bmatrix} 0.1 & -0.2 & 0.5 \\ 0.3 & 0.4 & 0.2 \\ 0.2 & 0.3 & -0.1 \\ 0.5 & -0.1 & 0.3 \end{bmatrix}\]Calculamos $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ multiplicando a matriz de entrada $\mathbf{X}$ pelas matrizes de peso correspondentes:
\[\mathbf{Q} = \mathbf{X}\mathbf{W}^Q\] \[\mathbf{K} = \mathbf{X}\mathbf{W}^K\] \[\mathbf{V} = \mathbf{X}\mathbf{W}^V\]Realizando as multiplicações (cálculos verificados):
\[\mathbf{Q} = \begin{bmatrix} 0.26 & 0.24 & -0.04 \\ -0.08 & 0.16 & 0.33 \\ 0.17 & 0.08 & 0.36 \end{bmatrix}\] \[\mathbf{K} = \begin{bmatrix} 0.03 & 0.31 & 0.11 \\ 0.26 & -0.11 & 0.12 \\ 0.34 & 0.07 & 0.03 \end{bmatrix}\] \[\mathbf{V} = \begin{bmatrix} 0.24 & 0.04 & 0.12 \\ 0.10 & -0.12 & 0.35 \\ 0.45 & 0.18 & 0.19 \end{bmatrix}\] -
Cálculo dos Scores de Atenção $(QK^T)$: calculamos os scores de atenção bruta multiplicando $\mathbf{Q}$ pela transposta de $\mathbf{K}$ ($\mathbf{K}^T$):
\[\mathbf{S_{raw}} = \mathbf{Q}\mathbf{K}^T\] \[\mathbf{K}^T = \begin{bmatrix} 0.03 & 0.26 & 0.34 \\ 0.31 & -0.11 & 0.07 \\ 0.11 & 0.12 & 0.03 \end{bmatrix}\] \[\mathbf{S_{raw}} = \begin{bmatrix} 0.26 & 0.24 & -0.04 \\ -0.08 & 0.16 & 0.33 \\ 0.17 & 0.08 & 0.36 \end{bmatrix} \begin{bmatrix} 0.03 & 0.26 & 0.34 \\ 0.31 & -0.11 & 0.07 \\ 0.11 & 0.12 & 0.03 \end{bmatrix} = \begin{bmatrix} 0.0778 & 0.0364 & 0.1040 \\ 0.0835 & 0.0012 & -0.0061 \\ 0.0695 & 0.0786 & 0.0742 \end{bmatrix}\]Em seguida, escalamos os scores dividindo pela raiz quadrada da dimensão das chaves ($\sqrt{d_k} = \sqrt{3} \approx 1.732$):
\[\text{Scores} = \frac{\mathbf{S_{raw}}}{\sqrt{d_k}} \approx \frac{\mathbf{S_{raw}}}{1.732}\] \[\text{Scores} \approx \begin{bmatrix} 0.0449 & 0.0210 & 0.0600 \\ 0.0482 & 0.0007 & -0.0035 \\ 0.0401 & 0.0454 & 0.0428 \end{bmatrix}\] -
Aplicação da Função Softmax: para cada linha da matriz
\[\mathbf{A} = \text{softmax}(\text{Scores})\]Scores, aplicamos a função softmax para obter pesos de atenção ($\mathbf{A}$) que somam $1$:Calculando o softmax para cada linha (arredondado para 4 casas decimais):
- Linha 1: $\text{softmax}([0.0449, 0.0210, 0.0600]) \approx [0.3343, 0.3264, 0.3393]$
- Linha 2: $\text{softmax}([0.0482, 0.0007, -0.0035]) \approx [0.3445, 0.3285, 0.3270]$
- Linha 3: $\text{softmax}([0.0401, 0.0454, 0.0428]) \approx [0.3324, 0.3342, 0.3334]$
Cada elemento $A_{ij}$ representa o quanto a palavra $i$ presta atenção à palavra $j$ ao construir sua representação de saída.
-
Multiplicação pelos Valores (V): finalmente, multiplicamos os pesos de atenção $\mathbf{A}$ pela matriz $\mathbf{V}$ para obter a saída final do mecanismo de atenção:
\[\text{Output} = \mathbf{A} \times \mathbf{V}\] \[\text{Output} \approx \begin{bmatrix} 0.3343 & 0.3264 & 0.3393 \\ 0.3445 & 0.3285 & 0.3270 \\ 0.3324 & 0.3342 & 0.3334 \end{bmatrix} \begin{bmatrix} 0.24 & 0.04 & 0.12 \\ 0.10 & -0.12 & 0.35 \\ 0.45 & 0.18 & 0.19 \end{bmatrix}\]Realizando o cálculo:
\[\text{Output} \approx \begin{bmatrix} 0.2655 & 0.0353 & 0.2188 \\ 0.2628 & 0.0333 & 0.2184 \\ 0.2632 & 0.0332 & 0.2202 \end{bmatrix}\]
Este é o resultado final da operação de atenção. Cada linha da matriz Output representa o novo vetor de contexto para a palavra correspondente na sequência de entrada ($\mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3$). Esse vetor agora incorpora informações ponderadas de todas as palavras da sequência, incluindo ela mesma, com base na relevância calculada pelo mecanismo de atenção.
Observamos que os pesos de atenção na matriz $\mathbf{A}$ estão relativamente equilibrados, todos próximos de $1/3 \approx 0.333$. Isso indica que, para estes embeddings de entrada e matrizes de peso $\mathbf{W}^Q, \mathbf{W}^K$ específicos, nenhuma palavra está prestando significativamente mais atenção a uma palavra específica do que às outras. Como resultado, os vetores na matriz Output são semelhantes a uma média ponderada quase uniforme dos vetores na matriz $\mathbf{V}$. Isso ocorre porque nossos embeddings de entrada são muito simples e pouco expressivos. Foram criados apenas para ilustrar o funcionamento do mecanismo de atenção.
Em um modelo Transformer real, os pesos $\mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V$ são aprendidos durante o treinamento em grandes volumes de dados. O objetivo é que o modelo aprenda a gerar matrizes $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ que resultem em padrões de atenção ($\mathbf{A}$) significativos e úteis para a tarefa em questão, destacando as interações relevantes entre as palavras.
Exemplo de Código C++
O código C++ abaixo ilustra a implementação do mecanismo de atenção com máscara, utilizando a biblioteca Eigen para operações matriciais e o exemplo numérico que vimos anteriormente. O código é modular e pode ser facilmente adaptado para diferentes sequências e máscaras.
#include <iostream> ///< Para entrada e saída padrão (std::cout).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de sequências.
#include <Eigen/Dense> ///< Para a biblioteca Eigen, usada em operações com matrizes e vetores.
#include <cmath> ///< Para funções matemáticas como std::exp e std::sqrt.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
/**
* @brief Aplica a função softmax elemento a elemento em uma linha de uma matriz Eigen.
* @param row Vetor de entrada representando uma linha da matriz (Eigen::VectorXd).
* @return Um novo vetor com a função softmax aplicada a cada elemento (Eigen::VectorXd).
*/
Eigen::VectorXd softmax(const Eigen::VectorXd& row) {
Eigen::VectorXd exp_row = row.array().exp();
double sum_exp = exp_row.sum();
if (sum_exp == 0.0) {
return Eigen::VectorXd::Zero(row.size()); // Evita divisão por zero
}
return exp_row / sum_exp;
}
/**
* @class ScaledDotProductAttention
* @brief Uma classe que implementa o mecanismo de Scaled Dot-Product Attention.
*
* Esta classe simula o mecanismo de atenção descrito em "Attention is All You Need",
* calculando os pesos de atenção com base em vetores Query, Key e Value, e produzindo
* uma saída ponderada. Utiliza a biblioteca Eigen para operações matriciais eficientes.
*/
class ScaledDotProductAttention {
private:
Eigen::MatrixXd W_Q; ///< Matriz de pesos para transformação Query (d x d_k).
Eigen::MatrixXd W_K; ///< Matriz de pesos para transformação Key (d x d_k).
Eigen::MatrixXd W_V; ///< Matriz de pesos para transformação Value (d x d_k).
double scale_factor; ///< Fator de escalonamento (raiz quadrada de d_k).
public:
/**
* @brief Construtor que inicializa as matrizes de pesos e o fator de escalonamento.
* @param w_q Matriz de pesos para Query (Eigen::MatrixXd).
* @param w_k Matriz de pesos para Key (Eigen::MatrixXd).
* @param w_v Matriz de pesos para Value (Eigen::MatrixXd).
*/
ScaledDotProductAttention(const Eigen::MatrixXd& w_q, const Eigen::MatrixXd& w_k,
const Eigen::MatrixXd& w_v)
: W_Q(w_q), W_K(w_k), W_V(w_v) {
scale_factor = std::sqrt(static_cast<double>(W_Q.cols()));
}
/**
* @brief Calcula o mecanismo de Scaled Dot-Product Attention para uma sequência de entrada.
* @param X Matriz de entrada contendo embeddings das palavras (n x d).
* @return Matriz de saída após o cálculo de atenção (n x d_k).
*/
Eigen::MatrixXd computeAttention(const Eigen::MatrixXd& X) const {
// Passo 1: Calcular Query, Key, Value
Eigen::MatrixXd Q = X * W_Q; // (n x d) * (d x d_k) = (n x d_k)
Eigen::MatrixXd K = X * W_K; // (n x d) * (d x d_k) = (n x d_k)
Eigen::MatrixXd V = X * W_V; // (n x d) * (d x d_k) = (n x d_k)
// Passo 2: Calcular scores de atenção brutos (QK^T)
Eigen::MatrixXd scores_raw = Q * K.transpose(); // (n x d_k) * (d_k x n) = (n x n)
// Passo 3: Escalonar os scores
Eigen::MatrixXd scores = scores_raw / scale_factor; // (n x n)
// Passo 4: Aplicar softmax para cada linha para obter pesos de atenção
Eigen::MatrixXd attention_weights(scores.rows(), scores.cols());
for (int i = 0; i < scores.rows(); ++i) {
attention_weights.row(i) = softmax(scores.row(i));
}
// Passo 5: Calcular a saída ponderada (AV)
Eigen::MatrixXd output = attention_weights * V; // (n x n) * (n x d_k) = (n x d_k)
return output;
}
/**
* @brief Exibe os resultados do cálculo de atenção, incluindo pesos e saída.
* @param X Matriz de entrada (Eigen::MatrixXd).
* @param output Matriz de saída após atenção (Eigen::MatrixXd).
*/
void printResults(const Eigen::MatrixXd& X, const Eigen::MatrixXd& output) const {
std::cout << "Matriz de Entrada (Embeddings, X):\n" << X << "\n\n";
// Recalcular pesos de atenção para exibição
Eigen::MatrixXd Q = X * W_Q;
Eigen::MatrixXd K = X * W_K;
Eigen::MatrixXd scores_raw = Q * K.transpose();
Eigen::MatrixXd scores = scores_raw / scale_factor;
Eigen::MatrixXd attention_weights(scores.rows(), scores.cols());
for (int i = 0; i < scores.rows(); ++i) {
attention_weights.row(i) = softmax(scores.row(i));
}
std::cout << "Pesos de Atenção (A = softmax(QK^T / sqrt(d_k))):\n";
std::cout << std::fixed << std::setprecision(4) << attention_weights << "\n\n";
std::cout << "Saída do Mecanismo de Atenção (Output = AV):\n";
std::cout << std::fixed << std::setprecision(4) << output << "\n";
}
};
/**
* @brief Função principal que demonstra o uso da classe ScaledDotProductAttention.
*
* Este programa simula o mecanismo de Scaled Dot-Product Attention usando os dados do exemplo
* numérico da seção "Atenção como Multiplicação de Matrizes". Uma sequência de 3 palavras com
* embeddings de dimensão 4 é processada, e os resultados são exibidos para análise.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
// Definir dimensões
int n = 3; ///< Número de palavras na sequência
int d = 4; ///< Dimensão dos embeddings
int d_k = 3; ///< Dimensão dos vetores Query, Key, Value
// Definir matriz de entrada X (3 palavras, embeddings de dimensão 4)
Eigen::MatrixXd X(n, d);
X << 0.2, -0.1, 0.5, 0.3, // x_1
0.5, 0.2, -0.3, 0.1, // x_2
-0.1, 0.4, 0.2, 0.6; // x_3
// Definir matrizes de pesos W_Q, W_K, W_V (4 x 3, conforme exemplo)
Eigen::MatrixXd W_Q(d, d_k);
W_Q << 0.1, 0.4, 0.2,
0.3, -0.2, 0.5,
0.6, 0.1, -0.3,
-0.1, 0.3, 0.4;
Eigen::MatrixXd W_K(d, d_k);
W_K << 0.2, 0.1, 0.3,
0.5, -0.3, 0.2,
-0.1, 0.4, 0.2,
0.3, 0.2, -0.1;
Eigen::MatrixXd W_V(d, d_k);
W_V << 0.1, -0.2, 0.5,
0.3, 0.4, 0.2,
0.2, 0.3, -0.1,
0.5, -0.1, 0.3;
// Criar instância do mecanismo de atenção
ScaledDotProductAttention attention(W_Q, W_K, W_V); ///< Instância do mecanismo de atenção
// Calcular atenção
Eigen::MatrixXd output = attention.computeAttention(X);
// Exibir resultados
attention.printResults(X, output);
return 0;
}
Processando o Contexto Ponderado: A Rede Feed-Forward
Após o mecanismo de atenção calcular o vetor de contexto $C_t$ para cada palavra $t$ (que agora contém informação da própria palavra $t$ misturada com informações ponderadas de outras palavras relevantes na sequência), precisamos processar essa representação contextual.
O nosso novo objetivo será transformar $C_t$ em uma saída que possa ser usada para a tarefa final, como prever a próxima palavra, ou que sirva como entrada para a próxima camada do modelo Transformer. Essa transformação é realizada por uma Rede Neural Feed-Forward (FFN), aplicada independentemente a cada posição $t$ da sequência.
Redes Feed-Forward (FFN) em Transformers
A Feed-Forward Network (FFN) nos Transformers é uma sub-rede neural aplicada independentemente a cada posição da sequência após o mecanismo de atenção.
Matematicamente, a FFN consiste em duas transformações lineares com uma não-linearidade entre elas:
\[\text{FFN}(C_t) = \max(0, C_t W_1 + b_1)W_2 + b_2\]Na qual, temos:
- $C_t$ é o vetor de contexto para a posição $t$ após o mecanismo de atenção;
- $W_1 \in \mathbb{R}^{d_{\text{model}} \times d_{\text{ff}}}$ e $W_2 \in \mathbb{R}^{d_{\text{ff}} \times d_{\text{model}}}$ são matrizes de peso;
- $b_1 \in \mathbb{R}^{d_{\text{ff}}}$ e $b_2 \in \mathbb{R}^{d_{\text{model}}}$ são vetores de bias;
- $\max(0, x)$ é a função de ativação ReLU (Rectified Linear Unit).
A primeira transformação linear tipicamente expande a dimensão ($d_{\text{ff}} \approx 4 \times d_{\text{model}}$), e a segunda projeta de volta para a dimensão original. Esta estrutura permite que a rede aprenda representações complexas e não-lineares do contexto capturado pelo mecanismo de atenção.
A FFN introduz capacidade de modelagem não-linear que complementa o mecanismo de atenção, permitindo que o Transformer aprenda funções mais complexas sobre as representações contextualizadas. Cada posição é processada independentemente, mantendo o paralelismo que é uma das vantagens-chave da arquitetura Transformer.
Embora tenhamos usado a analogia de “características de pares” na seção anterior, a FFN nos Transformers é mais genérica e poderosa. Tipicamente, ela consiste em duas camadas lineares com uma função de ativação não-linear entre elas, como ReLU (Rectified Linear Unit) ou GeLU (Gaussian Error Linear Unit):
\[\text{FFN}(C_t) = \text{ReLU}(C_t W_1 + b_1) W_2 + b_2\]Neste caso, $W_1, b_1, W_2, b_2$ são matrizes de pesos e vetores de bias aprendíveis. A primeira camada geralmente expande a dimensão do vetor $C_t$, e a segunda camada a projeta de volta para a dimensão original esperada pela próxima camada ou pela saída do modelo.
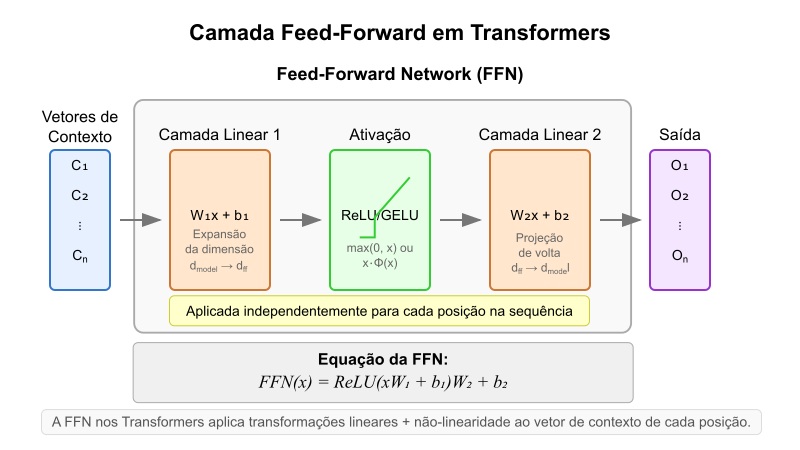 Figura 7: Diagrama conceitual de uma camada de rede neural. A FFN nosTransformersaplica transformações semelhantes (lineares + não-linearidade) ao vetor de contexto de cada posição.
Figura 7: Diagrama conceitual de uma camada de rede neural. A FFN nosTransformersaplica transformações semelhantes (lineares + não-linearidade) ao vetor de contexto de cada posição.
A não-linearidade (ReLU/GeLU) permite que a FFN aprenda transformações complexas e não apenas combinações lineares das informações presentes no vetor de contexto $C_t$.
Funções de Ativação: ReLU e GeLU
As funções de ativação não-lineares são componentes essenciais das redes neurais que permitem modelar relações complexas nos dados. Nos Transformers, duas funções de ativação são comumente usadas na camada Feed-Forward:
ReLU (Rectified Linear Unit):
A ReLU é definida matematicamente como:
\[\text{ReLU}(x) = \max(0, x)\]Esta função simples mantém valores positivos inalterados e converte valores negativos em zero. Suas vantagens incluem:
- Cálculo computacionalmente eficiente
- Mitigação do problema de gradientes que desaparecem
- Indução de esparsidade nas ativações
GeLU (Gaussian Error Linear Unit):
A GeLU, introduzida mais recentemente e usada em modelos como BERT e GPT, é definida como:
\[\text{GeLU}(x) = x \cdot \Phi(x)\]na qual temos: $\Phi(x)$ é a função de distribuição cumulativa da distribuição normal padrão. A GeLU pode ser aproximada por:
\[\text{GeLU}(x) \approx 0.5x \left(1 + \tanh\left(\sqrt{2/\pi}(x + 0.044715x^3)\right)\right)\]A GeLU suaviza a transição em torno de zero, ponderando cada valor de entrada pela probabilidade de ser positivo sob uma distribuição normal. Comparada à ReLU, a GeLU:
- Oferece gradientes não-nulos para entradas negativas
- Apresenta comportamento mais suave
- Frequentemente leva a melhor desempenho em tarefas de linguagem natural
Ambas as funções permitem que a rede neural aprenda representações não-lineares complexas dos dados de entrada, essenciais para o poder expressivo dos modelos Transformer modernos.
Embora possamos imaginar que a FFN poderia aprender a detectar combinações específicas como “bateria, executado”, como no exemplo manual abaixo, na prática ela aprende representações mais abstratas e úteis para a tarefa.
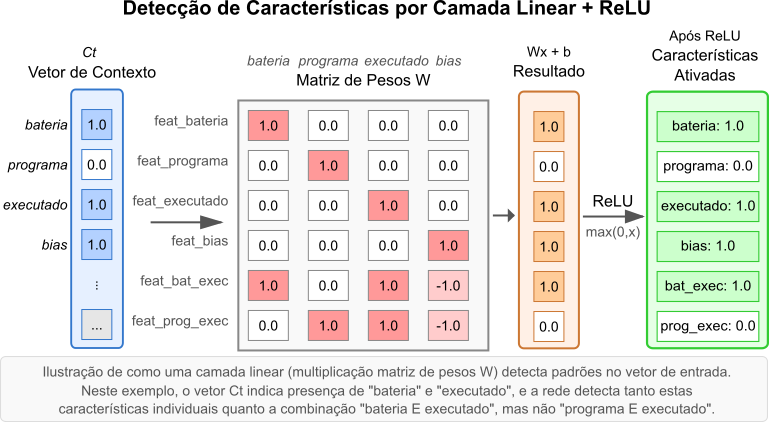 Figura 8: Ilustração de como uma camada linear (multiplicação por matriz de pesos W) pode, em princípio, ser configurada para detectar a presença/ausência de certas combinações no vetor de entrada (que seria o $C_t$ após a atenção). A ReLU subsequente ajudaria a “ativar” essas características detectadas.
Figura 8: Ilustração de como uma camada linear (multiplicação por matriz de pesos W) pode, em princípio, ser configurada para detectar a presença/ausência de certas combinações no vetor de entrada (que seria o $C_t$ após a atenção). A ReLU subsequente ajudaria a “ativar” essas características detectadas.
Exemplo de FFN em Código C++ 20
O código C++ abaixo demonstra a aplicação de uma camada linear seguida por ReLU, como parte de uma FFN:
#include <iostream> ///< Para entrada e saída padrão (std::cout).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de nomes de features.
#include <string> ///< Para std::string, usado em nomes de features e mensagens.
#include <unordered_map> ///< Para std::unordered_map (não utilizado diretamente neste código, mantido por compatibilidade).
#include <Eigen/Dense> ///< Para a biblioteca Eigen, usada em operações com matrizes e vetores.
#include <cmath> ///< Para std::max, usado na função ReLU.
/**
* @brief Aplica a função ReLU (Rectified Linear Unit) a um único valor.
* @param x O valor de entrada.
* @return O valor após a aplicação de ReLU, max(0, x) (double).
*/
double relu(double x) {
return std::max(0.0, x);
}
/**
* @brief Aplica a função ReLU elemento a elemento em um vetor Eigen.
* @param vec O vetor de entrada (Eigen::VectorXd).
* @return Um novo vetor com a função ReLU aplicada a cada elemento (Eigen::VectorXd).
*/
Eigen::VectorXd reluVector(const Eigen::VectorXd& vec) {
Eigen::VectorXd result = vec;
for (int i = 0; i < result.size(); ++i) {
result(i) = relu(result(i));
}
return result;
}
/**
* @class FeedForwardLayer
* @brief Uma classe que implementa uma camada feedforward com ativação ReLU.
*
* Esta classe simula uma camada de uma rede neural feedforward (FFN), aplicando uma transformação
* linear (W * x + b) seguida de uma ativação ReLU. Utiliza a biblioteca Eigen para operações matriciais
* e vetoriais.
*/
class FeedForwardLayer {
private:
Eigen::MatrixXd weights; ///< Matriz de pesos (W) da camada.
Eigen::VectorXd bias; ///< Vetor de bias (b) da camada.
std::vector<std::string> featureNames; ///< Nomes hipotéticos das features na saída.
public:
/**
* @brief Construtor que inicializa a camada com pesos, bias e nomes de features.
* @param w Matriz de pesos (Eigen::MatrixXd).
* @param b Vetor de bias (Eigen::VectorXd).
* @param names Vetor de strings contendo nomes das features de saída.
*/
FeedForwardLayer(const Eigen::MatrixXd& w, const Eigen::VectorXd& b, const std::vector<std::string>& names)
: weights(w), bias(b), featureNames(names) {}
/**
* @brief Aplica a transformação da camada (linear + ReLU) a um vetor de entrada.
* @param input O vetor de entrada (Eigen::VectorXd).
* @return O vetor de saída após a transformação linear e ativação ReLU (Eigen::VectorXd).
*/
Eigen::VectorXd forward(const Eigen::VectorXd& input) const {
Eigen::VectorXd hiddenOutput = weights * input + bias;
return reluVector(hiddenOutput);
}
/**
* @brief Exibe as features ativadas na saída da camada.
* @param output O vetor de saída após a transformação (Eigen::VectorXd).
*/
void printActivatedFeatures(const Eigen::VectorXd& output) const {
std::cout << "Features Ativadas (após ReLU) com nomes hipotéticos:\n";
for (size_t i = 0; i < output.size(); ++i) {
if (output(i) > 0) {
std::string name = (i < featureNames.size()) ? featureNames[i] : "Desconhecida";
std::cout << " " << name << ": " << output(i) << "\n";
}
}
}
};
/**
* @brief Função principal que demonstra o uso da classe FeedForwardLayer.
*
* Este programa simula uma camada feedforward com ativação ReLU, utilizando um vetor de contexto
* hipotético como entrada. A camada é configurada com pesos manuais para detectar combinações de
* features como "bateria", "executado", e outras, e os resultados são exibidos para análise.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
// Definir dimensões
int context_dim = 4; ///< Dimensão do vetor de contexto (entrada).
int hidden_dim = 8; ///< Dimensão da camada oculta (saída).
// Simular vetor de contexto C_t
Eigen::VectorXd context_vector = Eigen::VectorXd::Zero(context_dim);
context_vector(0) = 1.0; // Feature "bateria" ativa
context_vector(1) = 0.0; // Feature "programa" inativa
context_vector(2) = 1.0; // Feature "executado" ativa
context_vector(3) = 1.0; // Termo de bias
// Definir pesos e bias da camada
Eigen::MatrixXd W1(hidden_dim, context_dim);
Eigen::VectorXd b1(hidden_dim);
W1.setZero();
b1.setZero();
// Configurar pesos manuais
W1.row(0) << 1.0, 0.0, 0.0, 0.0; // Detecta "bateria"
W1.row(1) << 0.0, 1.0, 0.0, 0.0; // Detecta "programa"
W1.row(2) << 0.0, 0.0, 1.0, 0.0; // Detecta "executado"
W1.row(3) << 0.0, 0.0, 0.0, 1.0; // Detecta bias
W1.row(6) << 1.0, 0.0, 1.0, -1.0; // Detecta "bateria" E "executado"
W1.row(7) << 0.0, 1.0, 1.0, -1.0; // Detecta "programa" E "executado"
// Definir nomes hipotéticos para as features
std::vector<std::string> hidden_feature_names = {
"feat_bateria", "feat_programa", "feat_executado", "feat_bias",
"?", "?", "feat_bat_exec", "feat_prog_exec"
};
// Criar a camada feedforward
FeedForwardLayer layer(W1, b1, hidden_feature_names); ///< Instância da camada FFN.
// Aplicar a transformação
Eigen::VectorXd hidden_output = W1 * context_vector + b1;
Eigen::VectorXd activated_output = layer.forward(context_vector);
// Exibir resultados
std::cout << "Vetor de Contexto (Input C_t):\n" << context_vector.transpose() << "\n\n";
std::cout << "Saída da Camada Linear 1 (Antes de ReLU):\n" << hidden_output.transpose() << "\n\n";
std::cout << "Saída após ReLU (Input para Camada Linear 2):\n" << activated_output.transpose() << "\n\n";
// Exibir features ativadas
layer.printActivatedFeatures(activated_output);
return 0;
}
Portanto, um bloco típico de um Transformer consiste na aplicação do mecanismo de auto-atenção (para calcular o vetor de contexto $C_t$ para cada posição $t$, olhando para toda a sequência) seguido pela aplicação da Rede Feed-Forward (para processar cada $C_t$ independentemente). Frequentemente, conexões residuais e normalização de camada (Layer Normalization) são adicionadas em torno desses dois sub-blocos para facilitar o treinamento de redes profundas.
Conclusão e Perspectivas
Nesta jornada através da modelagem de sequências, partimos das Cadeias de Markov (modelos N-gram), reconhecendo sua simplicidade mas também suas limitações inerentes na captura de contexto de longo alcance. Vimos como a ideia conceitual de “pares com saltos” e “votação” nos levou à necessidade de um foco seletivo, que materializamos na intuição do mascaramento e da atenção seletiva.
Observamos como esse mecanismo de atenção pode ser implementado de forma eficiente e aprendível usando operações matriciais ($Q, K, V$ e a equação de atenção), permitindo ao modelo ponderar dinamicamente a relevância de diferentes partes da sequência. Finalmente, vimos como o vetor de contexto resultante é processado por uma Rede Feed-Forward (FFN), completando os dois componentes principais de um bloco Transformer.
A perspicaz leitora percebeu que construímos os fundamentos conceituais que justificam a arquitetura proposta em “Attention is All You Need”. Os Transformers abandonaram a recorrência das RNNs/LSTMs em favor da atenção paralelizável, permitindo treinar modelos muito maiores em mais dados e alcançando resultados estado-da-arte em inúmeras tarefas de Processamento de Linguagem Natural.
Claro, há mais detalhes na arquitetura completa do Transformer que não cobrimos aqui. Em um artigo futuro, iremos navegar em mares mais profundos, explorando:
- Atenção Multi-Cabeça (Multi-Head Attention): Como o modelo aprende a prestar atenção a diferentes aspectos da sequência simultaneamente.
- Codificação Posicional (Positional Encoding): Como a informação sobre a ordem das palavras, perdida pela atenção que trata a sequência como um conjunto, é reintroduzida.
- Arquitetura Completa Encoder-Decoder: Como esses blocos são empilhados e combinados para tarefas como tradução automática.
- Aplicações e Variações: Uma visão geral do impacto dos Transformers e modelos derivados (BERT, GPT, etc.).
Os conceitos que exploramos – modelagem sequencial, captura de contexto, e atenção seletiva – formam a base não apenas dos Transformers, mas de grande parte da pesquisa atual em inteligência artificial. Compreendê-los será como entender as nuances do mapa que o guiará nos vários mares do processamento de linguagens naturais.
Glossário - Transformers: Prestando Atenção
A
Agregação de Características de Pares Técnica que considera a influência de todos os pares $(w_i, w_t)$ formados pela palavra atual $w_t$ e cada palavra anterior $w_i$ na sequência, permitindo capturar dependências de longo alcance sem aumentar a ordem dos N-gramas.
Atenção (Attention) Mecanismo que permite ao modelo focar seletivamente em partes relevantes da sequência de entrada, calculado através da fórmula:
\[\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{QK^T}{\sqrt{d_k}} \right) V\]Atenção Seletiva Processo de focar dinamicamente nas características mais informativas, ignorando ou diminuindo o peso das demais através de técnicas como mascaramento.
Auto-atenção (Self-Attention) Mecanismo onde cada palavra em uma sequência presta atenção a todas as outras palavras da mesma sequência, incluindo a si mesma.
B
Backpropagation Algoritmo para calcular gradientes e atualizar pesos de modelos neurais através de operações matriciais diferenciáveis.
BERT (Bidirectional Encoder Representations from Transformers) Modelo baseado na arquitetura Transformer que processa texto bidirecionalmente.
C
Cadeias de Markov Processos estocásticos onde a probabilidade de um estado futuro depende apenas do estado presente, formalizados pela Propriedade de Markov:
\[P(X_{n+1} = x | X_1 = x_1, ..., X_n = x_n) = P(X_{n+1} = x | X_n = x_n)\]CBOW (Continuous Bag of Words) Arquitetura do Word2Vec que prediz a palavra atual a partir das palavras vizinhas.
D
Diluição do Sinal Problema onde a contribuição das características realmente informativas é reduzida pelo ruído das características menos úteis ao somar votos de muitas características.
Dot Product (Produto Escalar) Operação matemática usada para calcular similaridade entre vetores Query e Key no mecanismo de atenção.
E
Embedding Representação vetorial de palavras em um espaço contínuo de baixa dimensão $\vec{w} \in \mathbb{R}^d$ que captura propriedades semânticas e relações entre palavras.
Encoder-Decoder Arquitetura onde um encoder processa a sequência de entrada e um decoder gera a sequência de saída.
F
FastText Modelo de embedding que considera subpalavras (N-gramas de caracteres):
\[\vec{w} = \frac{1}{|G_w|} \sum_{g \in G_w} \vec{z}_g\]Feature (Característica) Propriedade do texto que contribui para a definição da próxima palavra, como pares $(w_i, w_t)$ no modelo de agregação.
Feed-Forward Network (FFN) Sub-rede neural aplicada independentemente a cada posição após o mecanismo de atenção:
\[\text{FFN}(C_t) = \max(0, C_t W_1 + b_1)W_2 + b_2\]G
GeLU (Gaussian Error Linear Unit) Função de ativação definida como:
\[\text{GeLU}(x) = x \cdot \Phi(x)\]Na qual, $\Phi(x)$ é a função de distribuição cumulativa da distribuição normal padrão.
GloVe (Global Vectors) Modelo de embedding que combina estatísticas globais de co-ocorrência com aprendizado local de contexto.
GPT (Generative Pre-trained Transformer) Modelo baseado na arquitetura Transformer para geração de texto.
H
Produto de Hadamard Multiplicação elemento a elemento entre matrizes de mesmas dimensões:
\[(A \circ B)_{ij} = A_{ij} \cdot B_{ij}\]K
Key (Chave) No mecanismo de atenção, vetor associado a cada palavra que pode ser comparado com a Query para determinar relevância, obtido através de $K = XW^K$.
L
Lei de Zipf Lei que governa a distribuição de frequências de palavras naturais:
\[f(k) \propto \frac{1}{k^s}\]Na qual $s \approx 1$ para linguagem natural.
LSTM (Long Short-Term Memory) Arquitetura de rede neural recorrente capaz de aprender dependências de longo prazo.
M
Maldição da Dimensionalidade Fenômeno onde a densidade de dados no espaço de N-gramas diminui exponencialmente conforme $N$ aumenta.
Máscara Vetor de pesos que atribui valores altos às características importantes e valores baixos às irrelevantes, aplicado através do produto Hadamard.
Mascaramento Técnica para zerar ou reduzir scores de posições não relevantes, permitindo foco seletivo em informações importantes.
Multi-Head Attention Mecanismo que executa múltiplas instâncias de atenção em paralelo, cada uma focando em diferentes aspectos da sequência.
N
N-grama Sequência contígua de $N$ itens (palavras) em um texto, onde o número de possíveis N-gramas únicos é $|V|^N$.
Normalização Processo de converter scores brutos em distribuições de probabilidade, frequentemente usando softmax.
O
Operações Matriciais Diferenciáveis Funções que mapeiam matrizes mantendo propriedades de diferenciabilidade, essenciais para algoritmos de otimização em aprendizado profundo.
P
Positional Encoding Técnica para reintroduzir informação sobre a ordem das palavras na arquitetura Transformer.
Produto Escalar Escalonado (Scaled Dot-Product) Mecanismo central do Transformer que calcula atenção através de:
\[\frac{QK^T}{\sqrt{d_k}}\]Propriedade de Markov Propriedade onde a probabilidade de um estado futuro depende apenas do estado presente, não de estados anteriores.
Q
Query (Consulta) No mecanismo de atenção, vetor que representa a palavra/posição atual, atuando como “sonda” para buscar informações relevantes, obtido através de $Q = XW^Q$.
R
ReLU (Rectified Linear Unit) Função de ativação definida como:
\[\text{ReLU}(x) = \max(0, x)\]RNN (Recurrent Neural Network) Arquitetura de rede neural que processa sequências de forma recorrente.
S
Self-Attention Ver Auto-atenção.
Similaridade de Cosseno Medida de similaridade entre vetores:
\[\text{sim}(\vec{w}_i, \vec{w}_j) = \frac{\vec{w}_i \cdot \vec{w}_j}{|\vec{w}_i| \cdot |\vec{w}_j|}\]Skip-gram Arquitetura do Word2Vec que prediz palavras vizinhas a partir da palavra atual.
Softmax Função que converte um vetor de números reais em distribuição de probabilidade:
\[\text{softmax}(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}}\]Smoothing (Suavização) Técnicas para lidar com N-gramas não observados durante o treinamento, evitando probabilidades zero.
T
Transformer Arquitetura de rede neural baseada exclusivamente em mecanismos de atenção, introduzida no artigo “Attention is All You Need”.
Transposta de Matriz Operação que troca linhas e colunas de uma matriz, denotada como $K^T$.
V
Value (Valor) No mecanismo de atenção, vetor contendo informação que será propagada se a palavra for considerada relevante, obtido através de $V = XW^V$.
Vetorização por Razão de Verossimilhança Técnica que compara padrões locais de um documento com padrões gerais do corpus.
Voto Na analogia de agregação de características, peso que uma característica específica atribui a uma palavra candidata como próxima palavra.
W
Word2Vec Modelo desenvolvido pelo Google para aprender embeddings de palavras usando redes neurais.
Símbolos Matemáticos
-
$ V $: Tamanho do vocabulário - $d$: Dimensão dos embeddings
- $d_k$: Dimensão dos vetores Key/Query
- $d_{model}$: Dimensão do modelo
- $d_{ff}$: Dimensão da camada feed-forward
- $w_t$: Palavra na posição $t$
- $C_t$: Vetor de contexto para posição $t$
- $\alpha_{ij}$: Peso de atenção entre posições $i$ e $j$
- $\mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V$: Matrizes de transformação para Query, Key e Value
Referências Bibliográficas
BAHDANAU, D.; CHO, K.; BENGIO, Y. Neural machine translation by jointly learning to align and translate. In: INTERNATIONAL CONFERENCE ON LEARNING REPRESENTATIONS, 3., 2015, San Diego. Proceedings […]. San Diego: ICLR, 2015.
BENGIO, Y. et al. A neural probabilistic language model. Journal of Machine Learning Research, v. 3, p. 1137-1155, 2003.
BROWN, P. F. et al. Class-based **N-gram models of natural language**. Computational Linguistics, v. 18, n. 4, p. 467-479, 1992.
CHOMSKY, N. Three models for the description of language. IRE Transactions on Information Theory, v. 2, n. 3, p. 113-124, 1956.
DEVLIN, J. et al. BERT: pre-training of deep bidirectional transformers for language understanding. In: CONFERENCE OF THE NORTH AMERICAN CHAPTER OF THE ASSOCIATION FOR COMPUTATIONAL LINGUISTICS, 2019, Minneapolis. Proceedings […]. Minneapolis: ACL, 2019. p. 4171-4186.
GRAVES, A. Supervised sequence labelling with recurrent neural networks. Heidelberg: Springer, 2012. (Studies in Computational Intelligence, v. 385).
HOCHREITER, S.; SCHMIDHUBER, J. Long short-term memory. Neural Computation, v. 9, n. 8, p. 1735-1780, 1997.
KINGMA, D. P.; BA, J. Adam: a method for stochastic optimization. In: INTERNATIONAL CONFERENCE ON LEARNING REPRESENTATIONS, 3., 2015, San Diego. Proceedings […]. San Diego: ICLR, 2015.
LUONG, M. T.; PHAM, H.; MANNING, C. D. Effective approaches to attention-based neural machine translation. In: CONFERENCE ON EMPIRICAL METHODS IN NATURAL LANGUAGE PROCESSING, 2015, Lisbon. Proceedings […]. Lisbon: ACL, 2015. p. 1412-1421.
MIKOLOV, T. et al. Distributed representations of words and phrases and their compositionality. In: ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS, 26., 2013, Lake Tahoe. Proceedings […]. Lake Tahoe: NIPS, 2013. p. 3111-3119.
RABINER, L. R. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE, v. 77, n. 2, p. 257-286, 1989.
SUTSKEVER, I.; VINYALS, O.; LE, Q. V. Sequence to sequence learning with neural networks. In: ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS, 27., 2014, Montreal. Proceedings […]. Montreal: NIPS, 2014. p. 3104-3112.
VASWANI, A. et al. Attention is all you need. In: ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS, 30., 2017, Long Beach. Proceedings […]. Long Beach: NIPS, 2017. p. 5998-6008.
