Transformers - Redes Neurais Artificiais para Word Embedding

Transformers - Redes Neurais Artificiais: Fundamentos
“What I cannot create, I do not understand.”
— Richard Feynman
Antes de viajarmos pelos algoritmos de representação distribuída de textos e, subsequentemente, pelos Transformers, é essencial que a amável leitora seja capaz de compreender como funcionam as redes neurais artificiais (RNAs). Essa será a base técnica sobre a qual construiremos, não apenas os modelos de embeddings, que utilizam redes neurais rasas como sua estrutura fundamental, mas também arquiteturas mais complexas como os próprios Transformers, que adaptam e expandem esses conceitos. Este artigo, guiará a jovem leitora exploradora pelos mares de conceitos, arquiteturas, e matemáticas que abrigam o treinamento das RNAs. Nesta viagem, estabeleceremos os alicerces necessários para a compreensão dos modelos de embeddings e pavimentaremos, assim espero, o caminho do entendimento dos Transformers.
Inspiração Biológica e Evolução Histórica
As redes neurais artificiais foram inspiradas pelo funcionamento do cérebro humano, especificamente pelos neurônios e suas conexões sinápticas. Os primeiros modelos matemáticos de neurônios artificiais datam de 1943, quando Warren McCulloch e Walter Pitts propuseram um modelo simplificado que representava o funcionamento básico de um neurônio biológico baseado apenas nas suposições da época sobre o funcionamento dos neurônios. Esse modelo inicial, embora rudimentar, lançou as bases para o desenvolvimento de redes neurais artificiais. McCulloch e Pitts propuseram que os neurônios poderiam ser representados como unidades lógicas, onde a ativação de um neurônio dependia da soma ponderada das entradas recebidas.
Em 1958, Frank Rosenblatt desenvolveu o Perceptron, um modelo algorítmico, para o reconhecimento de padrões baseado em uma rede neural de camada única. Apesar das limitações iniciais demonstradas por Marvin Minsky e Seymour Papert em 1969, como a incapacidade de resolver problemas não linearmente separáveis, as décadas seguintes trouxeram avanços significativos.
A popularização das redes neurais ressurgiu nos anos 1980 com a introdução do algoritmo de retropropagação (backpropagation) por Rumelhart, Hinton e Williams, possibilitando o treinamento eficiente de redes multicamadas. Este algoritmo permanece como a quilha que sustenta o navio do treinamento usado nas redes neurais modernas, incluindo as utilizadas em algoritmos de word embeddings como o CBoW e SkipGram.
O Neurônio Artificial
O elemento básico de uma rede neural artificial é o neurônio artificial, também chamado de unidade, vértice ou nó. Inspirado no neurônio biológico, ele recebe múltiplas entradas, processa-as e produz uma saída. A Figura 1 ilustra esta estrutura fundamental.
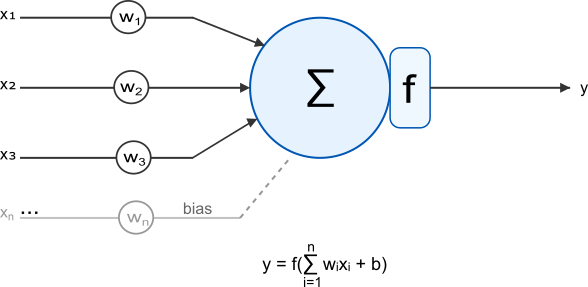
Figura 1: Representação de um neurônio artificial, mostrando entradas $(x₁, x₂, …, xₙ)$, pesos sinápticos $(w₁, w₂, …, wₙ)$, função de soma, bias ($b$) e função de ativação ($f$).
Matematicamente, o neurônio artificial pode ser descrito por:
\[y = f\left(\sum_{i=1}^{n} w_i x_i + b\right)\]Nesta equação, temos:
- $x_i$ são as entradas do neurônio;
- $w_i$ são os pesos associados a cada entrada;
- $b$ é o viés (bias), um termo que permite ajustar o limiar de ativação;
- $f$ é a função de ativação, que determina se, e como, o neurônio dispara com base na soma ponderada das entradas, $w_i x_i$, e do viés, $b$. Essa função acrescenta a não-linearidades ao modelo, permitindo que ele aprenda padrões mais complexos.
- $y$ é a saída do neurônio.
A soma ponderada $\sum_{i=1}^{n} w_i x_i$ pode ser vista de forma mais compacta como sendo o produto escalar entre o vetor de pesos $w = [w_1, …, w_n]$ e o vetor de entradas $x = [x_1, …, x_n]$, frequentemente denotado como $w \cdot x$ ou $w^T x$. Esta operação mede o quanto a entrada $x$ se alinha com os pesos $w$ aprendidos pelo neurônio. A atenta leitora deve lembrar que estudamos produto escalar em outro artigo.
A afirmação mais importante do parágrafo anterior “Esta operação mede o quanto a entrada $x$ se alinha com os pesos $w$ aprendidos pelo neurônio” refere-se a uma propriedade fundamental do produto escalar entre dois vetores. Matematicamente, o produto escalar entre os vetores $w$ e $x$ será calculado por:
\[w \cdot x = \sum_{i=1}^{n} w_i x_i = |w \vert \vert x \vert \cos(\theta)\]Neste caso, teremos:
- $\vert w \vert $ e $\vert x \vert $ são as magnitudes (normas) dos vetores;
- $\theta$ é o ângulo entre eles;
Esta formulação revela que o produto escalar é proporcional ao $\cos(\theta)$, que varia entre:
- $\cos(0°) = 1$ quando os vetores estão perfeitamente alinhados;
- $\cos(90°) = 0$ quando são perpendiculares;
- $\cos(180°) = -1$ quando estão em direções opostas.
No contexto de um neurônio artificial, o vetor de pesos $w$ representa uma direção no espaço de características que o neurônio aprendeu a reconhecer. Quando uma entrada $x$ tem alta similaridade direcional com $w$, seu produto escalar será grande e positivo, resultando em uma ativação mais forte. Inversamente, entradas que se alinham pouco ou se opõem à direção de $w$ produzirão valores baixos ou negativos.
Este é o princípio que a atenta leitora precisa governar para entender como as redes neurais aprendem a reconhecer padrões nos dados.
Vamos ilustrar o cálculo realizado por um neurônio artificial com um exemplo concreto. Suponha um neurônio artificial com duas entradas, pesos sinápticos correspondentes, um viés (bias) e a função de ativação Sigmóide. Dados por:
- Entradas (Inputs): $x = [x_1, x_2] = [0.5, 1.0]$
- Pesos (Weights): $w = [w_1, w_2] = [0.8, -0.2]$
- Viés (Bias): $b = 0.1$
- Função de Ativação: Sigmóide, $\sigma(z) = \frac{1}{1 + e^{-z} }$
Passo 1: Calcular a soma ponderada das entradas. Isso é o produto escalar entre os vetores de entrada e pesos: $w \cdot x = \sum_{i=1}^{n} w_i x_i$.
\[w \cdot x = w_1 x_1 + w_2 x_2 = (0.8 \times 0.5) + (-0.2 \times 1.0) = 0.4 + (-0.2) = 0.2\]Passo 2: Adicionar o viés (bias). Chamamos o resultado de $z$.
\[z = (w \cdot x) + b = 0.2 + 0.1 = 0.3\]Passo 3: Aplicar a função de ativação. A saída final $y$ é obtida aplicando a função Sigmóide a $z$.
\[y = \sigma(z) = \sigma(0.3) = \frac{1}{1 + e^{-0.3} }\]Para calcular $e^{-0.3}$, usamos uma calculadora (ou a função exp() em programação): $e^{-0.3} \approx 0.7408$.
Agora, substituímos na fórmula:
\[y = \frac{1}{1 + 0.7408} = \frac{1}{1.7408} \approx 0.5744\]Portanto, para as entradas $[0.5, 1.0]$, este neurônio específico produz uma saída de aproximadamente $0.5744$ com um arredondamento minimamente aceitável para quem fez na mão. As funções de ativação precisam de um pouco mais de atenção.
Funções de Ativação
As funções de ativação são componentes que determinam se um neurônio dispara e qual será sua saída. A atenta leitora deve lembrar que as funções de ativação introduzem não-linearidade às redes neurais. Sem funções de ativação não-lineares entre as camadas, uma rede neural profunda, de várias camadas, simplesmente colapsaria em uma única transformação linear equivalente, incapaz de modelar as relações complexas frequentemente encontradas em dados do mundo real. Isso acontece devido às propriedades fundamentais da álgebra linear.
Para entender este colapso, a curiosa leitora deve considerar uma rede neural com três camadas: uma de entrada, uma camada oculta e uma camada de saída sem funções de ativação não-lineares:
- Na camada oculta: $h = W^{(1)}x + b^{(1)}$
- Na camada de saída: $y = W^{(2)}h + b^{(2)}$
Substituindo a primeira equação na segunda:
\[y = W^{(2)}(W^{(1)}x + b^{(1)}) + b^{(2)}\] \[y = W^{(2)}W^{(1)}x + W^{(2)}b^{(1)} + b^{(2)}\]Esta expressão pode ser reescrita como:
\[y = W'x + b'\]Neste caso, temos:
- $W’ = W^{(2)}W^{(1)}$ (uma única matriz de transformação);
- $b’ = W^{(2)}b^{(1)} + b^{(2)}$ (um único vetor de viés);
Este fenômeno se estenderia para qualquer número de camadas lineares. Assim, uma rede profunda com $100$ camadas lineares seria matematicamente equivalente a uma rede com apenas uma camada. Isso significa que o poder representacional da rede não aumentaria com a adição de mais camadas.
As funções de ativação não-lineares (como $\text{ReLU}$, $\text{sigmóide}$ ou $\text{tanh}$) quebram esta propriedade de composição linear, permitindo que a rede aprenda mapeamentos mais complexos a cada camada adicional, possibilitando a modelagem de relações não-lineares presentes nos dados reais.
A escolha da função de ativação pode impactar significativamente o desempenho, graças a distribuição da não-linearidade, e a velocidade de treinamento da rede, graças ao custo computacional da função. As funções de ativação mais comuns incluem:
Função Degrau (Step Function)
\[\text{step}(x) = \begin{cases} 0, & \text{se } x < 0 \\ 1, & \text{se } x \geq 0 \end{cases}\]A função degrau é a mais simples das funções de ativação, produzindo apenas saídas binárias: $0$ ou $1$. Foi a primeira função de ativação utilizada no modelo original do Perceptron de Rosenblatt em 1958. Matematicamente, ela retorna $0$ para entradas negativas e $1$ para entradas não-negativas, criando uma transição abrupta no limiar zero.
A função degrau, quando aplicada a um valor $z$, produz resultados diretos:
- Se a entrada $z = 1.5$, a saída é $y = \text{step}(1.5) = 1$;
- Se a entrada $z = 0$, a saída é $y = \text{step}(0) = 1$;
- Se a entrada $z = -0.8$, a saída é $y = \text{step}(-0.8) = 0$.
Apesar de sua simplicidade conceitual, a função degrau apresenta uma limitação crítica para o treinamento de redes neurais: sua derivada é zero em todos os pontos exceto em $x = 0$, onde é indefinida. Isso torna impossível o uso do algoritmo de retropropagação, pois não há gradiente para propagar o erro. Por essa razão, funções diferenciáveis como $\text{sigmóide}$ e $\text{tanh}$ foram desenvolvidas como alternativas que aproximam o comportamento da função degrau, mas permitem o treinamento via gradiente descendente.
Função Sigmóide (ou Logística)
\[\sigma(x) = \frac{1}{1 + e^{-x} }\]A função sigmóide mapeia qualquer valor de entrada para o intervalo $(0, 1)$, tornando-a ideal para modelar probabilidades. Ela foi amplamente utilizada no passado, mas sofre de problemas como o desvanecimento do gradiente em redes profundas (veremos este problema adiante).
A função Sigmóide, dada por
\[\sigma(z) = \frac{1}{1 + e^{-z} }\]mapeia qualquer entrada para o intervalo, não-linear, $(0, 1)$.
- Se a entrada $z = 2.0$, $y = \sigma(2.0) = \frac{1}{1 + e^{-2.0} } \approx \frac{1}{1 + 0.1353} \approx 0.8808$;
- Se a entrada $z = 0.0$, $y = \sigma(0.0) = \frac{1}{1 + e^{0} } = \frac{1}{1 + 1} = 0.5$;
- Se a entrada $z = -3.0$, $y = \sigma(-3.0) = \frac{1}{1 + e^{-(-3.0)} } = \frac{1}{1 + e^{3.0} } \approx \frac{1}{1 + 20.0855} \approx 0.0474$.
Valores de entrada grandes positivos resultam em saídas próximas a $1$, e valores grandes negativos resultam em saídas próximas a $0$. A função é assintótica, ou seja, nunca atinge exatamente $0$ ou $1$, o que pode ser problemático em algumas situações. Além disso, a função sigmóide tem um gradiente muito pequeno para entradas extremas, o que pode levar ao problema do desvanecimento do gradiente durante o treinamento de redes profundas.
Função Tangente Hiperbólica (tanh)
\[\tanh(x) = \frac{e^x - e^{-x} }{e^x + e^{-x} }\]Similar à sigmóide, porém mapeia valores para o intervalo $(-1, 1)$, o que pode ajudar na convergência durante o treinamento por ter média zero. Contudo, assim como a sigmóide, a $\text{tanh}$ também sofre do problema de desvanecimento do gradiente em suas regiões saturadas, valores de entrada muito positivos ou muito negativos. Nestes dois limites a derivada se aproxima de zero. Isso limita o fluxo de gradientes em redes profundas.
Função ReLU (Rectified Linear Unit)
\[\text{ReLU}(x) = \max(0, x)\]Amplamente utilizada em redes neurais modernas por sua simplicidade computacional e eficácia no treinamento. A $\text{ReLU}$ simplesmente zera valores negativos e mantém os positivos. Embora muito popular, a $\text{ReLU}$ pode sofrer do problema do “neurônio morto”. Este problema ocorre quando a entrada é sempre negativa, o gradiente se torna zero e o neurônio para de aprender. Variantes como a Leaky ReLU, que permite um pequeno gradiente negativo ou a Parametric ReLU (PReLU) tentam mitigar esse problema.
A função $\text{ReLU}(x) = \max(0, x)$, é muito simples:
- Se a entrada $z = 3.5$, a saída é $y = \max(0, 3.5) = 3.5$;
- Se a entrada $z = -1.2$, a saída é $y = \max(0, -1.2) = 0$;
- Se a entrada $z = 0$, a saída é $y = \max(0, 0) = 0$.
A função simplesmente corta qualquer valor negativo, zerando-o, e mantém os valores positivos.
Função Softmax
\[\text{softmax}(x_i) = \frac{e^{x_i} }{\sum_{j=1}^{n} e^{x_j} }\]Utilizada especialmente na camada de saída para problemas de classificação multiclasse, tais como prever a próxima palavra em uma sequência.
No contexto de word embeddings, a função softmax será importante porque permite calcular probabilidades sobre todo o vocabulário, permitindo que a rede indique a palavra mais provável dada uma entrada. A função softmax transforma as pontuações das palavras em probabilidades transformando um vetor de valores reais, scores, em uma distribuição de probabilidades, garantindo que a soma seja $1$.
A função Softmax transforma um vetor de pontuações (logits) em um vetor de probabilidades. Para entender, suponha que a camada anterior produziu as seguintes pontuações para $3$ classes: $z = [z_1, z_2, z_3] = [2.0, 1.0, 0.1]$.
Passo 1: Calcular o exponencial de cada pontuação:
\[e^{z_1} = e^{2.0} \approx 7.389\] \[e^{z_2} = e^{1.0} \approx 2.718\] \[e^{z_3} = e^{0.1} \approx 1.105\]Passo 2: Calcular a soma de todos os exponenciais:
\[\sum_{j=1}^{3} e^{z_j} = e^{2.0} + e^{1.0} + e^{0.1} \approx 7.389 + 2.718 + 1.105 = 11.212\]Passo 3: Calcular a probabilidade Softmax para cada classe:
A probabilidade para a classe $i$ é $\text{softmax}(z_i) = \frac{e^{z_i} }{\sum_{j=1}^{3} e^{z_j} }$.
\[P(\text{classe 1} \vert z) = \frac{e^{z_1} }{\sum e^{z_j} } \approx \frac{7.389}{11.212} \approx 0.659\] \[P(\text{classe 2} \vert z) = \frac{e^{z_2} }{\sum e^{z_j} } \approx \frac{2.718}{11.212} \approx 0.242\] \[P(\text{classe 3} \vert z) = \frac{e^{z_3} }{\sum e^{z_j} } \approx \frac{1.105}{11.212} \approx 0.099\]O vetor de saída da função Softmax é $\vert{y} = [0.659, 0.242, 0.099]$. Note que a soma das probabilidades é $0.659 + 0.242 + 0.099 = 1.000$. A rede prevê a classe $1$ com maior probabilidade ($65.9\%$).
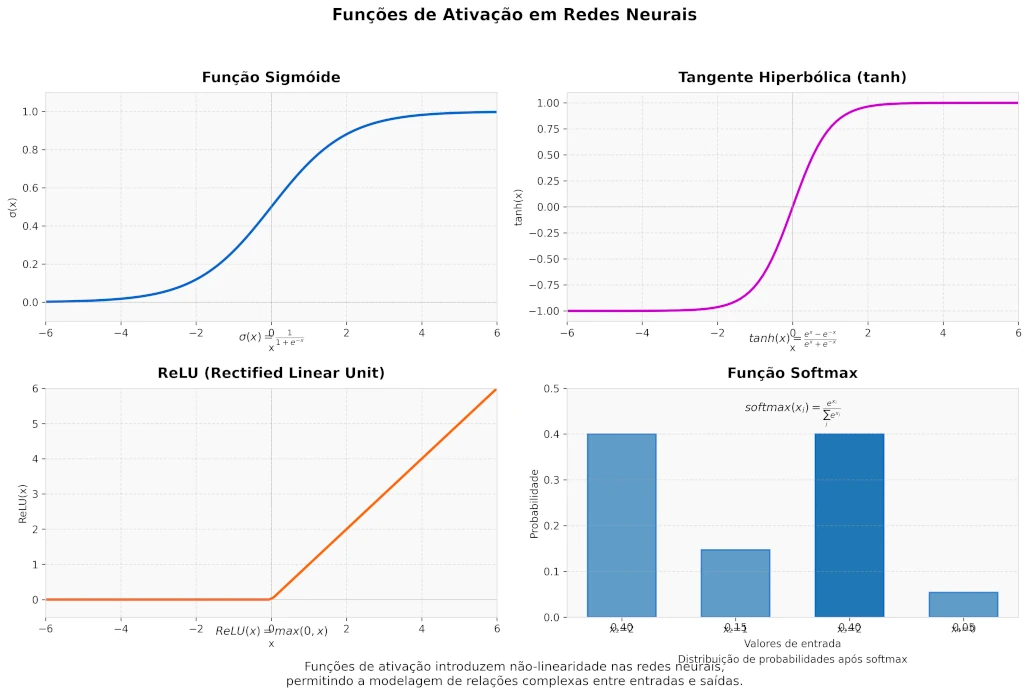
Figura 2: Principais funções de ativação utilizadas em redes neurais. No canto superior esquerdo, a função Sigmóide que mapeia valores para o intervalo $(0, 1)$. No canto superior direito, a função Tangente Hiperbólica ($tanh$) que mapeia valores para o intervalo $(-1, 1)$. No canto inferior esquerdo, a função ReLU (Rectified Linear Unit) que zera valores negativos e mantém os positivos. No canto inferior direito, a função Softmax que transforma um vetor de valores reais em uma distribuição de probabilidades.
Arquitetura de Redes Neurais
Com neurônios artificiais e funções de ativação definimos uma rede com uma camada. Esta é a arquitetura mais simples. Entretanto, as redes neurais podem ter arquiteturas mais diversificadas e complexas, definindo como os neurônios serão organizados e conectados. A compassiva leitora há de me perdoar mas vamos estudar apenas as arquiteturas mais relevantes para entender os modelos de embeddings.
Redes Feed-Forward (Alimentação Direta)
Uma rede neural feed-forward é a arquitetura mais simples, onde as informações se movem em uma única direção: da camada de entrada para a camada de saída. Não há ciclos ou laços na rede. A Figura 3 ilustra uma rede feed-forward com uma camada oculta.
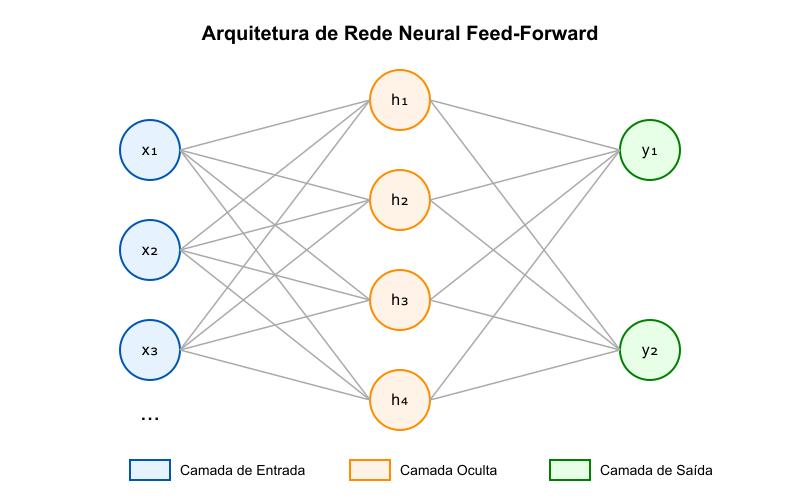
Figura 3: Arquitetura de uma rede neural feed-forward de três camadas, mostrando a camada de entrada, a camada oculta e a camada de saída.
Matematicamente, o processamento de uma entrada $x$ através de uma rede feed-forward com uma camada oculta pode ser representado como:
\[h_j = f\left(\sum_{i=1}^{n} w_{ji}^{(1)} x_i + b_j^{(1)}\right)\] \[y_k = g\left(\sum_{j=1}^{m} w_{kj}^{(2)} h_j + b_k^{(2)}\right)\]Em que, $f$ e $g$ são funções de ativação que introduzem não-linearidades essenciais, $w$ representa os pesos das conexões e $b$ os termos de viés.
Esta estrutura permite à rede aprender hierarquicamente: a camada oculta captura características intermediárias dos dados de entrada, enquanto a camada de saída combina essas características para produzir o resultado final. A ausência de conexões recorrentes simplifica o treinamento, tornando o algoritmo de retropropagação particularmente eficiente.
Em aplicações como word embeddings, as redes feed-forward rasas, com apenas uma camada oculta, são suficientes para capturar relações semânticas entre palavras. Porém, para tarefas mais complexas de reconhecimento de padrões, redes mais profundas com múltiplas camadas ocultas podem ser necessárias para modelar abstrações hierárquicas.
Cada transformação linear seguida por uma função de ativação não-linear aumenta o poder representacional da rede, permitindo-lhe aprender fronteiras de decisão progressivamente mais complexas que seriam impossíveis com o Perceptron de camada única.
Exemplo Numérico: Rede feed-forward com Diferentes Funções de Ativação
Considere uma rede neural feed-forward simples com:
- 2 neurônios na camada de entrada ($x = [x_1, x_2] = [0.5, 0.8]$);
- 3 neurônios na camada oculta (usando ReLU ou Sigmoid);
- 2 neurônios na camada de saída (usando Softmax).
-
Pesos e Vieses Definidos:
- $W^{(1)} = \begin{pmatrix} 0.1 & 0.2 & -0.1 \ -0.3 & 0.4 & 0.5 \end{pmatrix}^T$ (pesos entrada-oculta);
- $b^{(1)} = [0.1, -0.2, 0.3]$ (viés da camada oculta);
- $W^{(2)} = \begin{pmatrix} 0.6 & -0.3 \ -0.2 & 0.4 \ 0.5 & 0.1 \end{pmatrix}$ (pesos oculta-saída);
- $b^{(2)} = [0.2, 0.1]$ (viés da camada de saída).
-
Versão 1: $\text{ReLU}$ na Camada Oculta:
Passo 1: Calcular a entrada para a camada oculta.
$z^{(1)} = W^{(1)}x + b^{(1)}$
$z^{(1)}_1 = 0.1 \times 0.5 + (-0.3) \times 0.8 + 0.1 = -0.09$
$z^{(1)}_2 = 0.2 \times 0.5 + 0.4 \times 0.8 + (-0.2) = 0.22$
$z^{(1)}_3 = (-0.1) \times 0.5 + 0.5 \times 0.8 + 0.3 = 0.65$
Passo 2: Aplicar $\text{ReLU}$ à camada oculta. $h = ReLU(z^{(1)}) = \max(0, z^{(1)})$
$h_1 = \max(0, -0.09) = 0$
$h_2 = \max(0, 0.22) = 0.22$
$h_3 = \max(0, 0.65) = 0.65$
Passo 3: Calcular a entrada para a camada de saída. $z^{(2)} = W^{(2)}h + b^{(2)}$
$z^{(2)}_1 = 0.6 \times 0 + (-0.2) \times 0.22 + 0.5 \times 0.65 + 0.2 = 0.516$
$z^{(2)}_2 = (-0.3) \times 0 + 0.4 \times 0.22 + 0.1 \times 0.65 + 0.1 = 0.253$
Passo 4: Aplicar Softmax à camada de saída. $y = \text{softmax}(z^{(2)})$
\[y_1 = \frac{e^{0.516} }{e^{0.516} + e^{0.253} } = \frac{1.675}{1.675 + 1.288} = 0.565\] \[y_2 = \frac{e^{0.253} }{e^{0.516} + e^{0.253} } = \frac{1.288}{1.675 + 1.288} = 0.435\]A saída final da rede com ReLU é $y = [0.565, 0.435]$
-
Sigmoid na Camada Oculta:
Passo 1: Calcular a entrada para a camada oculta (igual ao anterior). $z^{(1)} = [-0.09, 0.22, 0.65]$
Passo 2: Aplicar Sigmoid à camada oculta. $h = \sigma(z^{(1)}) = \frac{1}{1 + e^{-z^{(1)} } }$
$h_1 = \frac{1}{1 + e^{0.09} } = \frac{1}{1.094} = 0.478$
$h_2 = \frac{1}{1 + e^{-0.22} } = \frac{1}{0.803} = 0.555$
$h_3 = \frac{1}{1 + e^{-0.65} } = \frac{1}{0.522} = 0.657$
Passo 3: Calcular a entrada para a camada de saída. $z^{(2)} = W^{(2)}h + b^{(2)}$
$z^{(2)}_1 = 0.6 \times 0.478 + (-0.2) \times 0.555 + 0.5 \times 0.657 + 0.2 = 0.637$
$z^{(2)}_2 = (-0.3) \times 0.478 + 0.4 \times 0.555 + 0.1 \times 0.657 + 0.1 = 0.222$
Passo 4: Aplicar Softmax à camada de saída. $y = \text{softmax}(z^{(2)})$
\[y_1 = \frac{e^{0.637} }{e^{0.637} + e^{0.222} } = \frac{1.891}{1.891 + 1.249} = 0.602\] \[y_2 = \frac{e^{0.222} }{e^{0.637} + e^{0.222} } = \frac{1.249}{1.891 + 1.249} = 0.398\]A saída final da rede com Sigmoid é $y = [0.602, 0.398]$
-
Comparação:
- ReLU: Produziu $y = [0.565, 0.435]$;
- Sigmoid: Produziu $y = [0.602, 0.398]$.
A diferença nos resultados ocorre porque a $\text{ReLU}$ desligou completamente o primeiro neurônio da camada oculta ($h_1 = 0$), enquanto a Sigmoid manteve esse neurônio parcialmente ativo ($h_1 = 0.478$), alterando a contribuição relativa de cada neurônio para a saída final. A escolha entre elas depende do problema específico, da arquitetura da rede e de outros fatores como por exemplo: o tipo dados sendo modelados; a profundidade da rede; Requisitos computacionais e o comportamento desejado para valores negativos.
Perceptron de Camada Única
O Perceptron de Rosenblatt é o exemplo mais simples de uma rede feed-forward, consistindo apenas de uma camada de neurônios de entrada diretamente conectada à camada de saída, geralmente com uma função de ativação degrau ou sigmóide. Esta estrutura é capaz de aprender e resolver apenas problemas que são linearmente separáveis, ou seja, problemas onde as classes podem ser separadas por um hiperplano no espaço de entrada.
Um problema é considerado não linearmente separável quando não é possível separar suas classes de dados usando uma única linha reta (ou hiperplano em dimensões maiores).
Por exemplo, o Perceptron pode aprender facilmente funções lógicas como AND e OR. No entanto, ele falha em problemas não linearmente separáveis, sendo o exemplo clássico desta falha, a função lógica XOR (OU exclusivo). Essa limitação teve impacto significativo na história das redes neurais. A incapacidade de aprender o comportamento de uma XOR demonstrou que o Perceptron de camada única não era suficiente para resolver muitos problemas práticos do mundo real. Isso motivou o desenvolvimento de redes multicamadas. Redes neurais artificiais que podem aprender fronteiras de decisão mais complexas e não-lineares, como veremos adiante. Essa incapacidade do Perceptron foi uma das críticas que levaram ao chamado inverno da IA nos anos 70. Essa limitação fundamental motivou o desenvolvimento de redes com múltiplas camadas.
Neste ponto, a curiosa leitora deve estar tentando entender porque existe essa limitação. Vamos explorar isso com um exemplo prático.
A função XOR é um exemplo clássico de problema não linearmente separável. Vamos analisar sua tabela verdade:
| Entrada $x_1$ | Entrada $x_2$ | Saída Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Se plotarmos esses pontos em um gráfico $2D$, com $x_1$ no eixo horizontal e $x_2$ no vertical:
- Temos pontos com saída $0$ em $(0,0)$ e $(1,1)$.
- Temos pontos com saída $1$ em $(0,1)$ e $(1,0)$.
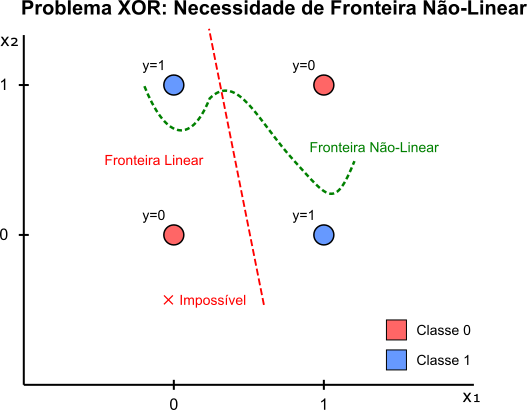
Figura 4: Representação visual do problema XOR e sua fronteira de decisão. Os pontos vermelhos representam saída $0$ $[(0,0) e (1,1)]$ e os pontos azuis representam saída $1$ $[(0,1) e (1,0)]$. A linha vermelha tracejada mostra a impossibilidade de separar estes pontos com uma única fronteira linear, enquanto a curva verde demonstra uma possível fronteira de decisão não-linear que uma rede neural com pelo menos uma camada oculta pode aprender.
O Perceptron de Camada Única funciona traçando uma única linha reta. ou um hiperplano em dimensões maiores, para separar as classes. Na Figura 4 não existe nenhuma linha reta única que consiga separar os pontos $(0,1)$ e $(1,0)$ de um lado, e os pontos $(0,0)$ e $(1,1)$ do outro. Você sempre acabará com um ponto do lado errado. É por isso que um Perceptron simples falha em aprender a função XOR. A solução requer uma rede com pelo menos uma camada oculta para criar uma fronteira de decisão não-linear.
Perceptron de Múltiplas Camadas (MLP)
A adição de camadas intermediárias, conhecidas como camadas ocultas, cria o Perceptron de Múltiplas Camadas (MLP). As camadas adicionais permitem que a rede aprenda representações hierárquicas e resolva problemas não lineares.
A estrutura básica de um Perceptron de Múltiplas Camadas inclui:
- Camada de entrada: recebe os dados brutos. Cada nó representa uma característica de entrada;
- Camadas ocultas: realizam transformações nos dados. O número e tamanho destas camadas são parte do conjunto de hiperparâmetros;
- Camada de saída: produz o resultado final da rede. Sua estrutura depende do tipo de problema, regressão, classificação binária ou multiclasse.
É importante que a esclarecida leitora note que cada camada que realiza uma multiplicação por uma matriz de pesos (como $W_{(1)}$ ou $W_{(2)}$) seguida pela adição de um viés ($b$) está, na verdade, aplicando uma transformação afim, uma transformação linear seguida por uma translação que estudamos aqui. A função de ativação não-linear que segue é fundamental. Sem a função de ativação, múltiplas camadas afins colapsariam em uma única transformação afim equivalente, limitando a capacidade de aprendizado da rede
Exemplo Numérico de uma Rede Neural com Transformações Afins
Este exemplo demonstra uma rede neural feed-forward com duas camadas ocultas e uma camada de saída, utilizando transformações afins ($W x + b$) seguidas de funções de ativação. A arquitetura é a seguinte:
- Camada de Entrada: $3$ neurônios, representando, por exemplo, um vetor de entrada simplificado para uma palavra em um espaço de embedding.
- Primeira Camada Oculta: $4$ neurônios com função de ativação ReLU.
- Segunda Camada Oculta: $3$ neurônios com função de ativação Tanh.
- Camada de Saída: $2$ neurônios com função de ativação Softmax, adequada para classificação ou previsão de probabilidades.
Abaixo, vamos calcular a propagação direta (forward pass) com valores específicos para ilustrar o funcionamento. Considerando os seguintes valores iniciais:
-
Entrada:
\[x = \begin{bmatrix} 1.0 \\ 0.5 \\ -0.2 \end{bmatrix}\] -
Pesos e Vieses:
-
Primeira Camada Oculta:
\[W^{(1)} = \begin{bmatrix} 0.2 & 0.3 & 0.1 \\ 0.4 & -0.1 & 0.5 \\ -0.2 & 0.6 & 0.0 \\ 0.1 & 0.0 & -0.3 \end{bmatrix}, \quad b^{(1)} = \begin{bmatrix} 0.1 \\ -0.2 \\ 0.3 \\ 0.0 \end{bmatrix}\] -
Segunda Camada Oculta:
\[W^{(2)} = \begin{bmatrix} 0.5 & -0.2 & 0.1 & 0.3 \\ 0.0 & 0.4 & -0.3 & 0.1 \\ -0.1 & 0.2 & 0.6 & -0.4 \end{bmatrix}, \quad b^{(2)} = \begin{bmatrix} 0.2 \\ -0.1 \\ 0.0 \end{bmatrix}\] -
Camada de Saída:
\[W^{(3)} = \begin{bmatrix} 0.3 & -0.5 & 0.2 \\ 0.1 & 0.4 & -0.6 \end{bmatrix}, \quad b^{(3)} = \begin{bmatrix} 0.1 \\ -0.2 \end{bmatrix}\]
-
Calculando passo a passo teremos:
-
Primeira Camada Oculta (ReLU):
Calculamos a transformação afim:
\[z^{(1)} = W^{(1)} x + b^{(1)} = \begin{bmatrix} 0.2 & 0.3 & 0.1 \\ 0.4 & -0.1 & 0.5 \\ -0.2 & 0.6 & 0.0 \\ 0.1 & 0.0 & -0.3 \end{bmatrix} \begin{bmatrix} 1.0 \\ 0.5 \\ -0.2 \end{bmatrix} + \begin{bmatrix} 0.1 \\ -0.2 \\ 0.3 \\ 0.0 \end{bmatrix}\]Calculando cada componente:
- \[z^{(1)}_1 = (0.2 \cdot 1.0) + (0.3 \cdot 0.5) + (0.1 \cdot -0.2) + 0.1 = 0.2 + 0.15 - 0.02 + 0.1 = 0.43\]
- \[z^{(1)}_2 = (0.4 \cdot 1.0) + (-0.1 \cdot 0.5) + (0.5 \cdot -0.2) - 0.2 = 0.4 - 0.05 - 0.1 - 0.2 = 0.05\]
- \[z^{(1)}_3 = (-0.2 \cdot 1.0) + (0.6 \cdot 0.5) + (0.0 \cdot -0.2) + 0.3 = -0.2 + 0.3 + 0.0 + 0.3 = 0.4\]
- \[z^{(1)}_4 = (0.1 \cdot 1.0) + (0.0 \cdot 0.5) + (-0.3 \cdot -0.2) + 0.0 = 0.1 + 0.0 + 0.06 = 0.16\]
Portanto:
\[z^{(1)} = \begin{bmatrix} 0.43 \\ 0.05 \\ 0.4 \\ 0.16 \end{bmatrix}\]Aplicamos a função ReLU:
\[h^{(1)} = \text{ReLU}(z^{(1)}) = \begin{bmatrix} \max(0, 0.43) \\ \max(0, 0.05) \\ \max(0, 0.4) \\ \max(0, 0.16) \end{bmatrix} = \begin{bmatrix} 0.43 \\ 0.05 \\ 0.4 \\ 0.16 \end{bmatrix}\] -
Segunda Camada Oculta ($\text{Tanh}$)
Calculamos a transformação afim:
\[z^{(2)} = W^{(2)} h^{(1)} + b^{(2)} = \begin{bmatrix} 0.5 & -0.2 & 0.1 & 0.3 \\ 0.0 & 0.4 & -0.3 & 0.1 \\ -0.1 & 0.2 & 0.6 & -0.4 \end{bmatrix} \begin{bmatrix} 0.43 \\ 0.05 \\ 0.4 \\ 0.16 \end{bmatrix} + \begin{bmatrix} 0.2 \\ -0.1 \\ 0.0 \end{bmatrix}\]Calculando cada componente:
- \[z^{(2)}_1 = (0.5 \cdot 0.43) + (-0.2 \cdot 0.05) + (0.1 \cdot 0.4) + (0.3 \cdot 0.16) + 0.2 = 0.215 - 0.01 + 0.04 + 0.048 + 0.2 = 0.493\]
- \[z^{(2)}_2 = (0.0 \cdot 0.43) + (0.4 \cdot 0.05) + (-0.3 \cdot 0.4) + (0.1 \cdot 0.16) - 0.1 = 0.0 + 0.02 - 0.12 + 0.016 - 0.1 = -0.184\]
- \[z^{(2)}_3 = (-0.1 \cdot 0.43) + (0.2 \cdot 0.05) + (0.6 \cdot 0.4) + (-0.4 \cdot 0.16) + 0.0 = -0.043 + 0.01 + 0.24 - 0.064 = 0.143\]
Portanto:
\[z^{(2)} = \begin{bmatrix} 0.493 \\ -0.184 \\ 0.143 \end{bmatrix}\]Aplicamos a função Tanh:
\(h^{(2)} = \tanh(z^{(2)}) = \begin{bmatrix} \tanh(0.493) \\ \tanh(-0.184) \\ \tanh(0.143) \end{bmatrix} \approx \begin{bmatrix} 0.452 \\ -0.180 \\ 0.141 \end{bmatrix}\) (valores aproximados usando uma calculadora).
-
Camada de Saída (Softmax):
Calculamos a transformação afim:
\[z^{(3)} = W^{(3)} h^{(2)} + b^{(3)} = \begin{bmatrix} 0.3 & -0.5 & 0.2 \\ 0.1 & 0.4 & -0.6 \end{bmatrix} \begin{bmatrix} 0.452 \\ -0.180 \\ 0.141 \end{bmatrix} + \begin{bmatrix} 0.1 \\ -0.2 \end{bmatrix}\]Calculando cada componente:
- \[z^{(3)}_1 = (0.3 \cdot 0.452) + (-0.5 \cdot -0.180) + (0.2 \cdot 0.141) + 0.1 = 0.1356 + 0.09 + 0.0282 + 0.1 = 0.3538\]
- \[z^{(3)}_2 = (0.1 \cdot 0.452) + (0.4 \cdot -0.180) + (-0.6 \cdot 0.141) - 0.2 = 0.0452 - 0.072 - 0.0846 - 0.2 = -0.3114\]
Portanto:
\[z^{(3)} = \begin{bmatrix} 0.3538 \\ -0.3114 \end{bmatrix}\]Aplicamos a função Softmax:
\[y = \text{Softmax}(z^{(3)}) = \begin{bmatrix} \frac{e^{0.3538} }{e^{0.3538} + e^{-0.3114} } \\ \frac{e^{-0.3114} }{e^{0.3538} + e^{-0.3114} } \end{bmatrix}\]Calculando os exponenciais:
- \[e^{0.3538} \approx 1.424\]
- \[e^{-0.3114} \approx 0.732\]
Assim:
\[y \approx \begin{bmatrix} \frac{1.424}{1.424 + 0.732} \\ \frac{0.732}{1.424 + 0.732} \end{bmatrix} = \begin{bmatrix} \frac{1.424}{2.156} \\ \frac{0.732}{2.156} \end{bmatrix} \approx \begin{bmatrix} 0.660 \\ 0.340 \end{bmatrix}\] -
Resultado:
A saída da rede neural é:
\[y = \begin{bmatrix} 0.660 \\ 0.340 \end{bmatrix}\]Isso representa as probabilidades para duas classes, demonstrando como as transformações afins e as funções de ativação processam a entrada através da rede.
Implementação em C++ 20 de um Perceptron de Múltiplas Camadas
#include <iostream>
#include <Eigen/Dense>
#include <stdexcept>
#include <format>
#include <concepts>
#include <ranges>
#include <span>
using Eigen::MatrixXd;
using Eigen::VectorXd;
/**
* @brief Conceito para tipos que podem ser usados em operações vetoriais
*/
template <typename T>
concept VectorLike = requires(T a, T b) {
{ a + b } -> std::convertible_to<T>;
{ a - b } -> std::convertible_to<T>;
{ a * std::declval<double>() } -> std::convertible_to<T>;
};
/**
* @brief Aplica a função de ativação ReLU elemento a elemento
* @tparam Vector Tipo do vetor de entrada (deve satisfazer o conceito VectorLike)
* @param x Vetor de entrada
* @return Vetor com ReLU aplicado
*/
template <VectorLike Vector>
Vector relu(const Vector& x) {
return x.array().max(0);
}
/**
* @brief Aplica a função de ativação Tanh elemento a elemento
* @tparam Vector Tipo do vetor de entrada (deve satisfazer o conceito VectorLike)
* @param x Vetor de entrada
* @return Vetor com Tanh aplicado
*/
template <VectorLike Vector>
Vector tanh(const Vector& x) {
return x.array().tanh();
}
/**
* @brief Aplica a função Softmax a um vetor
* @tparam Vector Tipo do vetor de entrada (deve satisfazer o conceito VectorLike)
* @param x Vetor de pontuações
* @return Vetor de probabilidades
*/
template <VectorLike Vector>
Vector softmax(const Vector& x) {
Vector exp_x = (x.array() - x.maxCoeff()).exp(); // Estabilidade numérica
return exp_x / exp_x.sum();
}
/**
* @brief Verifica as dimensões das matrizes e vetores para compatibilidade
* @throws std::invalid_argument Se as dimensões forem incompatíveis
*/
void verificar_dimensoes(const VectorXd& x,
const MatrixXd& W1, const VectorXd& b1,
const MatrixXd& W2, const VectorXd& b2,
const MatrixXd& W3, const VectorXd& b3) {
if (W1.cols() != x.size()) {
throw std::invalid_argument(
std::format("Incompatibilidade de dimensões: W1({},{}) e x({})",
W1.rows(), W1.cols(), x.size()));
}
if (W1.rows() != b1.size()) {
throw std::invalid_argument(
std::format("Incompatibilidade de dimensões: W1({},{}) e b1({})",
W1.rows(), W1.cols(), b1.size()));
}
if (W2.cols() != W1.rows()) {
throw std::invalid_argument(
std::format("Incompatibilidade de dimensões: W2({},{}) e W1({},{})",
W2.rows(), W2.cols(), W1.rows(), W1.cols()));
}
if (W2.rows() != b2.size()) {
throw std::invalid_argument(
std::format("Incompatibilidade de dimensões: W2({},{}) e b2({})",
W2.rows(), W2.cols(), b2.size()));
}
if (W3.cols() != W2.rows()) {
throw std::invalid_argument(
std::format("Incompatibilidade de dimensões: W3({},{}) e W2({},{})",
W3.rows(), W3.cols(), W2.rows(), W2.cols()));
}
if (W3.rows() != b3.size()) {
throw std::invalid_argument(
std::format("Incompatibilidade de dimensões: W3({},{}) e b3({})",
W3.rows(), W3.cols(), b3.size()));
}
}
/**
* @brief Propaga a entrada através da rede neural
* @param x Vetor de entrada
* @param W1, b1 Pesos e viés da 1ª camada
* @param W2, b2 Pesos e viés da 2ª camada
* @param W3, b3 Pesos e viés da camada de saída
* @return Vetor de saída (probabilidades)
* @throws std::invalid_argument Se as dimensões forem incompatíveis
*/
VectorXd propagacao_direta(const VectorXd& x,
const MatrixXd& W1, const VectorXd& b1,
const MatrixXd& W2, const VectorXd& b2,
const MatrixXd& W3, const VectorXd& b3) {
// Verificar dimensões das matrizes e vetores
verificar_dimensoes(x, W1, b1, W2, b2, W3, b3);
// Primeira camada oculta: ReLU(W1 * x + b1)
VectorXd h1 = relu(W1 * x + b1);
// Segunda camada oculta: Tanh(W2 * h1 + b2)
VectorXd h2 = tanh(W2 * h1 + b2);
// Camada de saída: Softmax(W3 * h2 + b3)
return softmax(W3 * h2 + b3);
}
/**
* @brief Estrutura para armazenar os parâmetros da rede neural
*/
struct RedeNeuralParams {
VectorXd x; // Entrada
MatrixXd W1; // Pesos da 1ª camada
VectorXd b1; // Viés da 1ª camada
MatrixXd W2; // Pesos da 2ª camada
VectorXd b2; // Viés da 2ª camada
MatrixXd W3; // Pesos da camada de saída
VectorXd b3; // Viés da camada de saída
};
/**
* @brief Inicializa os parâmetros da rede com os valores do exemplo numérico
* @return Estrutura contendo todos os parâmetros inicializados
*/
RedeNeuralParams inicializar_parametros() {
RedeNeuralParams params;
params.x.resize(3);
params.x << 1.0, 0.5, -0.2;
params.W1.resize(4, 3);
params.W1 << 0.2, 0.3, 0.1,
0.4, -0.1, 0.5,
-0.2, 0.6, 0.0,
0.1, 0.0, -0.3;
params.b1.resize(4);
params.b1 << 0.1, -0.2, 0.3, 0.0;
params.W2.resize(3, 4);
params.W2 << 0.5, -0.2, 0.1, 0.3,
0.0, 0.4, -0.3, 0.1,
-0.1, 0.2, 0.6, -0.4;
params.b2.resize(3);
params.b2 << 0.2, -0.1, 0.0;
params.W3.resize(2, 3);
params.W3 << 0.3, -0.5, 0.2,
0.1, 0.4, -0.6;
params.b3.resize(2);
params.b3 << 0.1, -0.2;
return params;
}
/**
* @brief Imprime um vetor formatado
* @param label Rótulo para o vetor
* @param vetor Vetor a ser impresso
*/
void imprimir_vetor(std::string_view label, const VectorXd& vetor) {
std::cout << std::format("{} =\n", label);
for (int i = 0; i < vetor.size(); ++i) {
std::cout << std::format("{:.4f}\n", vetor[i]);
}
std::cout << '\n';
}
/**
* @brief Função principal
*/
int main() {
try {
std::cout << "Rede Neural com Transformações Afins\n";
std::cout << "------------------------------------\n\n";
// Inicialização dos parâmetros
auto params = inicializar_parametros();
// Exibir entrada
imprimir_vetor("Entrada x", params.x);
// Propagação direta
VectorXd saida = propagacao_direta(
params.x,
params.W1, params.b1,
params.W2, params.b2,
params.W3, params.b3
);
// Exibir saída
imprimir_vetor("Saída da Rede (Softmax)", saida);
} catch (const std::exception& e) {
std::cerr << std::format("Erro: {}\n", e.what());
return 1;
}
return 0;
}
Redes Neurais Rasas vs. Profundas
No contexto de word embeddings, utilizamos redes neurais rasas.Ou seja, com poucas camadas ocultas, geralmente apenas uma. Estas redes são suficientes para aprender representações distribuídas de palavras. Estas são redes neuras Perceptron de Múltiplas Camadas simplificadas que utilizam apenas uma camada oculta. Elas são eficazes para tarefas simples de aprendizado de máquina, como classificação de texto ou análise de sentimentos.
Em contraste, as redes profundas contêm múltiplas camadas ocultas, às vezes dezenas ou centenas. Estas redes profundas, em inglês deep networks, podem aprender representações mais complexas e abstratas, sendo essenciais para tarefas como reconhecimento de imagens ou alguns algoritmos específicos no domínio dos Transformers.
Arquitetura Rasa dos Modelos de Embeddings
A arquitetura dos modelos de word embeddings é notavelmente simples:
- Uma camada de entrada: representa a(s) palavra(s) utilizando codificação One-Hot;
- Uma camada oculta linear: sem função de ativação não-linear;
- Uma camada de saída: com ativação softmax para calcular a probabilidade de cada palavra do vocabulário.
A simplicidade arquitetural dos modelos de word embeddings é intencionalmente proposital por quatro razões fundamentais: eficiência computacional. Modelos menos complexos exigem menos recursos e treinam mais rapidamente com grandes corpora textuais; alinhamento com a semântica distribucional, teoria linguística que propõe que $p(contexto \vert palavra)$ revela significados semânticos através de padrões estatísticos de co-ocorrência; preservação da linearidade conceitual, já que a ausência de funções não-lineares na camada oculta mantém propriedades algébricas que permitem operações vetoriais como:
\[\vec{v}_{rei} - \vec{v}_{homem} + \vec{v}_{mulher} \;\; \approx \vec{v}_{rainha}\]criando um espaço vetorial onde relações semânticas são representadas por transformações lineares $T: \mathbb{R}^d \rightarrow \mathbb{R}^d$; e validação empírica, pois experimentos demonstraram que essa estrutura minimalista $f(x) = W_2 \cdot (W_1 \cdot x)$ produz representações surpreendentemente eficazes sem necessidade de arquiteturas mais elaboradas. Esta é a arquitetura que veremos nos modelos de word embeddings e no artigo publicado aqui.
Representação e Propagação de Dados
Para compreender como as redes neurais processam informações, a atenta leitora precisa visualizar o fluxo dinâmico dos dados através da rede. Esta trajetória dos sinais desde a camada de entrada até a produção do resultado final revela a essência do processamento neuronal artificial. Quando um vetor de entrada $\mathbf{x}$ é apresentado à rede, ele inicia uma cascata de transformações matemáticas onde cada camada subsequente extrai e refina padrões específicos. Os dados percorrem este labirinto de neurônios artificiais através de operações vetoriais que incluem produtos escalares $\mathbf{w} \cdot \mathbf{x}$, adições de vieses $b$, e transformações não-lineares $f(\cdot)$ que introduzem a capacidade da rede de modelar relações complexas. É nesta corrente oceânica de números navegando de camada em camada que reside o verdadeiro poder das redes neurais, permitindo-lhes lançar redes mais profundas que capturam os cardumes semânticos das palavras que buscamos em nossa expedição pelos mares da linguagem natural.
Nesta correnteza de dados, a propagação direta é o motor que impulsiona a rede, transformando entradas em saídas através de uma série de etapas matemáticas que revelam a beleza e complexidade do aprendizado profundo.
Propagação Direta (Forward Propagation)
Como a esperta leitora já deve ter deduzido, a propagação direta é o processo pelo qual uma entrada percorre a rede, da camada de entrada até a camada de saída. Para uma rede feed-forward com uma camada oculta, o processo pode ser descrito matematicamente por meio do seguinte conjunto de equações:
-
Cálculo das ativações da camada oculta:
\[h_j = f\left(\sum_{i=1}^{n} w_{ji}^{(1)} x_i + b_j^{(1)}\right)\] -
Cálculo das ativações da camada de saída:
\[y_k = g\left(\sum_{j=1}^{m} w_{kj}^{(2)} h_j + b_k^{(2)}\right)\]
No qual, temos:
- $x_i$ são as entradas da rede;
- $h_j$ são as ativações da camada oculta;
- $y_k$ são as saídas da rede;
- $w_{ji}^{(1)}$ e $w_{kj}^{(2)}$ são os pesos das conexões;
- $b_j^{(1)}$ e $b_k^{(2)}$ são os termos de viés;
- $f$ e $g$ são funções de ativação, possivelmente diferentes.
No contexto dos modelos de word embeddings e Transformers, a propagação direta é usada para calcular a probabilidade de uma palavra-alvo dado seu contexto ou vice-versa. Para tentar entender como isso funciona, vamos fazer um exemplo numérico simples. Vamos calcular a propagação direta para uma rede neural feed-forward pequena. Considere uma rede com:
- 2 neurônios de entrada;
- 1 camada oculta com 2 neurônios, usando Sigmóide como função de ativação $f$;
- 1 neurônio de saída, usando Sigmóide como função de ativação $g$.
Notação:
- $x = [x_1, x_2]$: Vetor de entrada;
- $W^{(1)}$: Matriz de pesos da camada de entrada para a oculta (dimensão 2x2);
- $b^{(1)}$: Vetor de vieses da camada oculta (dimensão 2x1);
- $h = [h_1, h_2]$: Vetor de ativação da camada oculta;
- $W^{(2)}$: Matriz (vetor linha) de pesos da camada oculta para a saída (dimensão 1x2);
- $b^{(2)}$: Viés da camada de saída (escalar);
- $y$: Saída final da rede (escalar).
Valores de Exemplo:
- Entrada: $x = \begin{pmatrix} 1.0 \ 0.5 \end{pmatrix}$;
- Pesos Camada 1: $W^{(1)} = \begin{pmatrix} 0.2 & 0.4 \ -0.5 & 0.1 \end{pmatrix}$;
- Vieses Camada 1: $b^{(1)} = \begin{pmatrix} 0.1 \ -0.2 \end{pmatrix}$;
- Pesos Camada 2: $W^{(2)} = \begin{pmatrix} 0.7 & -0.3 \end{pmatrix}$;
- Viés Camada 2: $b^{(2)} = 0.0$.
Passo 1: Calcular a entrada ponderada e a ativação da Camada Oculta ($h$). Primeiro, calcule $z^{(1)} = W^{(1)}x + b^{(1)}$.
\[z^{(1)} = \begin{pmatrix} 0.2 & 0.4 \\ -0.5 & 0.1 \end{pmatrix} \begin{pmatrix} 1.0 \\ 0.5 \end{pmatrix} + \begin{pmatrix} 0.1 \\ -0.2 \end{pmatrix}\]Calculando a multiplicação matriz-vetor:
\[\begin{pmatrix} (0.2 \times 1.0) + (0.4 \times 0.5) \\ (-0.5 \times 1.0) + (0.1 \times 0.5) \end{pmatrix} = \begin{pmatrix} 0.2 + 0.2 \\ -0.5 + 0.05 \end{pmatrix} = \begin{pmatrix} 0.4 \\ -0.45 \end{pmatrix}\]Adicionando o viés $b^{(1)}$:
\[z^{(1)} = \begin{pmatrix} 0.4 \\ -0.45 \end{pmatrix} + \begin{pmatrix} 0.1 \\ -0.2 \end{pmatrix} = \begin{pmatrix} 0.4 + 0.1 \\ -0.45 + (-0.2) \end{pmatrix} = \begin{pmatrix} 0.5 \\ -0.65 \end{pmatrix}\]Agora, aplique a função de ativação Sigmóide ($f = \sigma$) elemento a elemento em $z^{(1)}$ para obter $h$:
\[h = \sigma(z^{(1)}) = \begin{pmatrix} \sigma(0.5) \\ \sigma(-0.65) \end{pmatrix} = \begin{pmatrix} \frac{1}{1 + e^{-0.5} } \\ \frac{1}{1 + e^{-(-0.65)} } \end{pmatrix} \approx \begin{pmatrix} \frac{1}{1 + 0.6065} \\ \frac{1}{1 + 1.9155} \end{pmatrix} \approx \begin{pmatrix} 0.6225 \\ 0.3430 \end{pmatrix}\]Portanto, a ativação da camada oculta é $h \approx [0.6225, 0.3430]$.
Passo 2: Calcular a entrada ponderada e a ativação da Camada de Saída ($y$).
Primeiro, calcule $z^{(2)} = W^{(2)}h + b^{(2)}$.
\[z^{(2)} = \begin{pmatrix} 0.7 & -0.3 \end{pmatrix} \begin{pmatrix} 0.6225 \\ 0.3430 \end{pmatrix} + 0.0\]Calculando a multiplicação matriz-vetor (produto escalar aqui):
\[z^{(2)} = (0.7 \times 0.6225) + (-0.3 \times 0.3430) + 0.0 \approx 0.43575 - 0.1029 + 0.0 = 0.33285\]Agora, aplique a função de ativação Sigmóide ($g = \sigma$) a $z^{(2)}$ para obter a saída final $y$:
\[y = \sigma(z^{(2)}) = \sigma(0.33285) = \frac{1}{1 + e^{-0.33285} } \approx \frac{1}{1 + 0.7169} \approx 0.5824\]A saída final da rede para a entrada $x = [1.0, 0.5]$ é aproximadamente $y = 0.5824$.
Representação de Palavras como Vetores
Para processar palavras em uma rede neural, precisamos convertê-las em representações numéricas. A abordagem tradicional é a codificação One-hot que vimos aqui.
Para um vocabulário de tamanho $ \vert V \vert $, cada palavra será representada por um vetor de dimensão $ \vert V \vert $ com valor $1$ na posição correspondente à palavra e $0$ nas demais posições. Por exemplo, em um vocabulário de $5$ palavras:
\[V = \{\text{gato}, \text{cachorro}, \text{pássaro}, \text{corre}, \text{dorme}\}\]As representações one-hot seriam:
gato= $[1, 0, 0, 0, 0]$;cachorro= $[0, 1, 0, 0, 0]$;pássaro= $[0, 0, 1, 0, 0]$;corre= $[0, 0, 0, 1, 0]$;dorme= $[0, 0, 0, 0, 1]$.
Nos modelos de word embeddings, estas representações One-Hot são transformadas em embeddings densos através da camada oculta da rede neural. Esses embeddings são vetores de dimensão reduzida que capturam a semântica e o contexto das palavras. A ideia é que palavras com significados semelhantes tenham representações vetoriais próximas no espaço vetorial. Veremos estes vetores neste artigo.
Treinamento de Redes Neurais
As Redes Neurais Artificiais são algoritmos fantásticos. Mas, como qualquer algoritmo supervisionado, elas precisam ser treinadas. O treinamento é o processo de ajuste dos pesos e vieses da rede para minimizar a diferença entre as previsões da rede e os valores reais desejados. Este treinamento será feito, na maior parte das vezes, por meio de um processo iterativo chamado retropropagação, backpropagation, em inglês.
Os algoritmos de treinamento de uma rede neural envolvem ajustar seus pesos e vieses para minimizar a diferença entre suas previsões e os valores reais desejados. Este processo é importante, interessante e fascinante. Porém, tem limitações.
Desvanecimento e Explosão de Gradientes
Um desafio significativo no treinamento de redes neurais, especialmente as mais profundas, aquelas com muitas camadas, ou recorrentes, aquelas que processam sequências longas, consiste no problema dos gradientes que desvanecem (vanishing gradients, em inglês) ou explodem (exploding gradients, novamente, em inglês). Estes problemas surgem devido à natureza das funções de ativação e à forma como os gradientes são calculados durante a retropropagação. Eles podem levar a dificuldades no treinamento, resultando em redes que não aprendem ou que divergem rapidamente. Estes fenômenos têm as seguintes características:
-
Vanishing Gradients (Desvanecimento): durante a retropropagação, os gradientes são calculados aplicando-se sucessivamente a regra da cadeia. Se as derivadas parciais forem consistentemente pequenas, menores que $1$, como acontece nas regiões de saturação das funções sigmóide e $\text{tanh}$, onde a curva é quase plana, o gradiente pode diminuir exponencialmente à medida que navegamos para as camadas iniciais da rede. Isso resulta em atualizações de peso insignificantes, fazendo com que os pesos das camadas iniciais da rede não sejam ajustados adequadamente. Como resultado, a rede pode não aprender ou aprender muito lentamente, levando a um desempenho insatisfatório. Este fenômeno é especialmente problemático em redes profundas, onde o número de camadas pode exacerbar o problema.
-
Exploding Gradients (Explosão): o problema oposto pode ocorrer se as derivadas forem consistentemente grandes, maiores que $1$. O gradiente pode crescer exponencialmente, resultando em atualizações de peso enormes que desestabilizam o treinamento, levando a valores numéricos muito grandes que, via de regra, resultam em $NaN$ - $Not a Number$ em computadores que usem a Norma IEEE-754.
Embora este texto foque em redes rasas para embeddings, nas quais estes problemas são menos severos, a esforçada leitora precisa deve se preocupar com o impacto desses fenômenos no treinamento de redes neurais mais profundas. Estas redes profundas são típicas dos modelos de LLM’s que se tornaram muito populares depois de 2023. Para tanto, vamos preparar o barco para esta outra viagem, já discutindo algumas soluções comuns para esses problemas:
-
Motiva a escolha de funções de ativação como a ReLU, que não satura para entradas positivas, sua derivada é $1$, ajudando a mitigar o desvanecimento, embora possa levar a neurônios mortos.
-
Explica a necessidade de técnicas como inicialização cuidadosa de pesos, como a Xavier/He, que visam manter a magnitude dos gradientes estável.
-
Introduz a necessidade de técnicas como gradient clipping, limitar a magnitude máxima do gradiente durante o treinamento, para combater a explosão de gradientes.
-
Contextualiza o desenvolvimento de arquiteturas mais complexas como LSTMs/GRUs (em redes recorrentes) e mecanismos como conexões residuais (nos Transformers) que foram projetados, em parte, para lidar com esses problemas de fluxo de gradiente.
Inicialização de Pesos Xavier/Glorot e He
A inicialização adequada dos pesos é importante para o treinamento eficiente de redes neurais profundas. As inicializações Xavier/Glorot e He foram desenvolvidas para manter a variância dos sinais e gradientes estável através das camadas da rede.
Inicialização Xavier/Glorot: proposta por Xavier Glorot e Yoshua Bengio (2010), esta inicialização é adequada para funções de ativação com comportamento aproximadamente linear na origem (sigmóide, tanh). Dada por:
Para uma camada com $n_{in}$ entradas e $n_{out}$ saídas:
\[W \sim \mathcal{U}\left[-\frac{\sqrt{6} }{\sqrt{n_{in} + n_{out} } }, \frac{\sqrt{6} }{\sqrt{n_{in} + n_{out} } }\right]\]Ou na versão com distribuição normal:
\[W \sim \mathcal{N}\left(0, \frac{2}{n_{in} + n_{out} }\right)\]Visa manter a variância da ativação e dos gradientes aproximadamente igual entre as camadas, evitando que o sinal se perca ou exploda durante a propagação.
Inicialização He
Desenvolvida por Kaiming He et al. (2015), esta inicialização é otimizada para funções de ativação ReLU e suas variantes, que não são simétricas em torno da origem.
Para uma camada com $n_{in}$ entradas:
\[W \sim \mathcal{N}\left(0, \frac{2}{n_{in} }\right)\]Como ReLU zera metade da distribuição (valores negativos), a inicialização He compensa esse efeito usando um fator $2$ no numerador, garantindo que a variância se mantenha correta após a aplicação da função de ativação.
Ambas as inicializações permitem treinar redes profundas muito mais rapidamente e com maior estabilidade, sendo essenciais para o sucesso do aprendizado profundo moderno.
Função de Custo (Loss Function)
A função de custo é uma medida quantitativa que avalia a discrepância entre as previsões geradas pela rede neural e os valores esperados, também chamados de alvos. Em problemas de classificação multiclasse, como a predição da próxima palavra em uma sequência textual, a entropia cruzada é frequentemente adotada devido à sua eficácia. Esta função penaliza fortemente as previsões incorretas enquanto recompensa as corretas, sendo definida matematicamente como:
\[L = -\sum_{i=1}^{n} y_i \log(\vert{y}_i)\]na qual $y_i$ representa o valor real da classe $i$, geralmente $1$ para a classe correta e $0$ para as demais, $\vert{y}_i$ indica a probabilidade atribuída pelo modelo à classe $i$, e $n$ corresponde ao número total de classes. A minimização desta função durante o treinamento direciona o modelo a maximizar a probabilidade associada à classe correta.
No contexto dos word embeddings, isto se traduz em maximizar a probabilidade da palavra correta.
Vamos calcular a entropia cruzada para um exemplo de classificação multiclasse com $3$ classes. Suponha que:
- Vetor de probabilidades previsto pela rede (saída do Softmax): $\vert{y} = [0.1, 0.7, 0.2]$;
- Vetor alvo real (one-hot encoded): $y = [0, 1, 0]$, este vetor indica que a classe correta é a segunda.
A fórmula da entropia cruzada para um único exemplo é:
\[L = -\sum_{i=1}^{n} y_i \log(\vert{y}_i)\]Na qual, $n=3$ é o número de classes e $\log$ é o logaritmo natural.
Substituindo os valores, teremos:
\[L = - [ (y_1 \times \log(\vert{y}_1)) + (y_2 \times \log(\vert{y}_2)) + (y_3 \times \log(\vert{y}_3)) ]\] \[L = - [ (0 \times \log(0.1)) + (1 \times \log(0.7)) + (0 \times \log(0.2)) ]\]Como $0 \times \text{qualquer coisa} = 0$, a fórmula simplifica em:
\[L = - [ 0 + (1 \times \log(0.7)) + 0 ] = - \log(0.7)\]Usando uma calculadora encontramos $\log(0.7) \approx -0.3567$.
\[L = -(-0.3567) = 0.3567\]O custo, erro, para este exemplo é aproximadamente $0.3567$. Quanto menor o custo, melhor a previsão da rede, a probabilidade $\vert{y}_i$ da classe correta $y_i=1$ está mais próxima de $$1$. Se a rede tivesse previsto $\vert{y} = [0.01, 0.98, 0.01]$, o custo seria $L = -\log(0.98) \approx 0.02$, um valor muito menor.
Gradiente Descendente
O gradiente descendente é um algoritmo de otimização fundamental usado para ajustar os parâmetros da rede, pesos e vieses, de forma a minimizar a função de custo. A ideia central é calcular como a função de custo $L$ muda em relação a cada parâmetro ajustável da rede e, então, dar um pequeno passo na direção que diminui o custo. Gradiente é um termo para a taxa de variação de uma função em relação a suas variáveis. Em termos geométricos, o gradiente aponta na direção de maior aumento da função. Portanto, para minimizar a função de custo, precisamos mover na direção oposta ao gradiente.Por isso, o descendente no nome.
Seja $\theta$ um símbolo genérico para representar qualquer parâmetro ajustável na rede, como um peso $w_{ij}$ ou um viés $b_j$. O processo envolve calcular o gradiente da função de custo em relação a um parâmetro específico $\theta_j$. Ou seja, a derivada parcial $\frac{\partial L}{\partial \theta_j}$ e atualizar o valor desse parâmetro na direção oposta ao gradiente:
\[\theta_j \leftarrow \theta_j - \eta \frac{\partial L}{\partial \theta_j}\]Em que:
- $\theta_j$ é um parâmetro específico na rede (um peso ou viés);
- $\eta$ (eta) é la taxa de aprendizado (learning rate), um hiperparâmetro que controla o tamanho do passo de atualização;
- $\frac{\partial L}{\partial \theta_j}$ é la derivada parcial da função de custo $L$ em relação ao parâmetro $\theta_j$. Este valor indica a sensibilidade do custo a pequenas mudanças em $\theta_j$.

Figura 5: Mostra, graficamente o conceito do gradiente descendente em um gráfico de curvas de nível.
A atualização de um único parâmetro ($\theta_j$) usando Gradiente Descendente é direta. Suponha que para um determinado parâmetro $\theta_j$:
- Valor atual do parâmetro: $\theta_j = 0.8$;
- Taxa de aprendizado: $\eta = 0.01$ (um valor pequeno, comum na prática);
- Gradiente da função de custo em relação a este parâmetro (calculado via backpropagation): $\frac{\partial L}{\partial \theta_j} = -2.5$, o sinal negativo indica que aumentar $\theta_j$ diminuiria o custo $L$.
A fórmula de atualização será dada por:
\[\theta_j \leftarrow \theta_j - \eta \frac{\partial L}{\partial \theta_j}\]Usando alguns os valores hipotéticos teremos:
\[\theta_j \leftarrow 0.8 - (0.01 \times (-2.5))\] \[\theta_j \leftarrow 0.8 - (-0.025)\] \[\theta_j \leftarrow 0.8 + 0.025 = 0.825\]O novo valor do parâmetro $\theta_j$ será $0.825$. Como o gradiente era negativo, a atualização aumentou o valor do parâmetro, movendo-o na direção que, localmente, diminui o custo. Se o gradiente fosse positivo, digamos $+1.5$, a atualização seria $\theta_j \leftarrow 0.8 - (0.01 \times 1.5) = 0.8 - 0.015 = 0.785\;$, diminuindo o valor do parâmetro.
Retropropagação (Backpropagation)
A retropropagação, Backpropagation em inglês, é o algoritmo que permite calcular eficientemente esses gradientes em redes multicamadas. A ideia central é usar a regra da cadeia do cálculo diferencial. A regra da cadeia nos permite calcular a derivada de uma função composta, essencial para entender como o erro na saída da rede se relaciona com os pesos em cada camada.
A Regra da Cadeia na Retropropagação
A regra da cadeia do cálculo diferencial é o princípio matemático que viabiliza todo o algoritmo de retropropagação. Ela permite calcular derivadas de funções compostas. Este é exatamente o caso que temos em redes neurais de multiplas camadas, onde a saída de uma camada é a entrada da próxima. A regra da cadeia afirma que, se temos uma função composta $f(g(x))$, a derivada de $f$ em relação a $x$ pode ser expressa como o produto das derivadas de $f$ e $g$:
\[\frac{d}{dx}[f(g(x))] = \frac{df}{dg} \cdot \frac{dg}{dx}\]Aplicação na Retropropagação:
- A função de custo $L$ depende das saídas $\vert{y}$;
- As saídas $\vert{y}$ dependem das ativações $z^{(L)}$;
- As ativações $z^{(L)}$ dependem dos pesos $w$ e ativações anteriores.
Para calcular $\frac{\partial L}{\partial w_{ji}^{(l)} }$, encadeamos estas derivadas:
\[\frac{\partial L}{\partial w_{ji}^{(l)} } = \frac{\partial L}{\partial z_j^{(l)} } \cdot \frac{\partial z_j^{(l)} }{\partial w_{ji}^{(l)} }\]Onde $\frac{\partial L}{\partial z_j^{(l)} } = \delta_j^{(l)}$ (o erro do neurônio) e $\frac{\partial z_j^{(l)} }{\partial w_{ji}^{(l)} } = a_i^{(l-1)}$ (a ativação da camada anterior).
Caso Especial: Entropia Cruzada + Sigmóide
Uma propriedade matemática notável ocorre quando combinamos entropia cruzada como função de custo e sigmóide como ativação de saída. Aplicando a regra da cadeia:
\[\delta_k^{(L)} = \frac{\partial L}{\partial z_k^{(L)} } = \frac{\partial L}{\partial \vert{y}_k} \cdot \frac{\partial \vert{y}_k}{\partial z_k^{(L)} }\]Para entropia cruzada: $\frac{\partial L}{\partial \vert{y}_k} = -\frac{y_k}{\vert{y}_k} + \frac{1-y_k}{1-\vert{y}_k}$
Para sigmóide: $\frac{\partial \vert{y}_k}{\partial z_k^{(L)} } = \vert{y}_k(1-\vert{y}_k)$
Multiplicando: $\delta_k^{(L)} = (-\frac{y_k}{\vert{y}_k} + \frac{1-y_k}{1-\vert{y}_k}) \cdot \vert{y}_k(1-\vert{y}_k) = \vert{y}_k - y_k$
Esta simplificação elegante é o que torna a combinação entropia cruzada + sigmóide computacionalmente eficiente.
O algoritmo de retropropagação começa com o cálculo do erro na camada de saída, a diferença entre a previsão $\vert{y}$ e o alvo $y$. Em seguida, esse erro é propagado para trás, em direção a camada de entrada na rede, esta é a origem do nome retropropagação, camada por camada. Em cada camada, calcula-se o quanto cada neurônio contribuiu para o erro da camada seguinte.
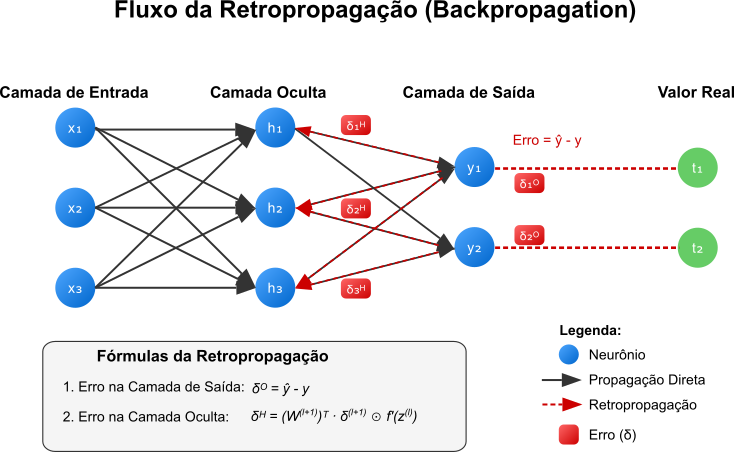
Figura 6: Fluxo do algoritmo de retropropagação. O erro é calculado na camada de saída e propagado para trás, camada por camada, ajustando os pesos conforme necessário. A seta azul representa o fluxo do erro, enquanto a seta vermelha representa o fluxo dos gradientes.
Isso permite determinar o gradiente da função de custo em relação aos pesos de cada conexão, informando como ajustar esses pesos para reduzir o erro geral da rede. O processo pode ser resumido nos seguintes passos:
-
Calcular o erro na camada de saída:
\[\delta_k^{(L)} = \frac{\partial L}{\partial z_k^{(L)} } = \vert{y}_k - y_k\]Por que a simplificação $\delta^{(L)} = \vert{y} - y$ é válida para entropia cruzada + sigmóide?
A simplificação ocorre devido à cancelamento matemático entre a derivada da função de custo, entropia cruzada e a derivada da função de ativação, sigmóide. Veja a derivação:
Função de Custo (Entropia Cruzada Binária):
\[L = -y \log(\vert{y}) - (1 - y) \log(1 - \vert{y})\]Neste caso, $\vert{y} = \sigma(z)$ é a saída da sigmóide.
Derivada de $L$ em relação a $z$:
Pela regra da cadeia:
\[\delta^{(L)} = \frac{\partial L}{\partial z} = \frac{\partial L}{\partial \vert{y} } \cdot \frac{\partial \vert{y} }{\partial z}\]Cálculo de $\frac{\partial L}{\partial \vert{y} }$:
\[\frac{\partial L}{\partial \vert{y} } = -\frac{y}{\vert{y} } + \frac{1 - y}{1 - \vert{y} }\]Derivada da Sigmóide: \(\frac{\partial \vert{y} }{\partial z} = \vert{y}(1 - \vert{y})\)
Combinação das Derivadas:
\[\delta^{(L)} = \left(-\frac{y}{\vert{y} } + \frac{1 - y}{1 - \vert{y} }\right) \cdot \vert{y}(1 - \vert{y})\]Simplificando:
\[\delta^{(L)} = -y(1 - \vert{y}) + (1 - y)\vert{y} = \vert{y} - y\]O termo $\vert{y}(1 - \vert{y})$, derivada da sigmóide, cancela-se com os denominadores da entropia cruzada, resultando na expressão simplificada $\delta^{(L)} = \vert{y} - y$. Isso só é possível porque:
- A entropia cruzada é projetada para “casar” com a função sigmóide.
-
Propagar o erro para camadas anteriores:
\[\delta_j^{(l)} = \left(\sum_{k} \delta_k^{(l+1)} w_{kj}^{(l+1)}\right) f'(z_j^{(l)})\] -
Calcular os gradientes dos pesos:
\[\frac{\partial L}{\partial w_{ji}^{(l)} } = \delta_j^{(l)} a_i^{(l-1)}\]
Neste caso, temos:
- $\delta$ representa o erro em cada neurônio;
- $z$ é a entrada da função de ativação;
- $f’$ é a derivada da função de ativação;
- $a$ é a ativação do neurônio.
Exemplo Prático de Retropropagação
Contexto: queremos calcular o gradiente para o peso $w_{12}^{(2)}$, que conecta o neurônio $h_2$ da camada oculta (camada $l=2$) ao neurônio $y_1$ da camada de saída.
Dados do Exemplo:
- Ativação da camada anterior: $a_2^{(1)} = h_2 \approx 0.3430$ (calculado na propagação direta);
- Saída da rede: $\vert{y} = 0.5824$ (previsão).
- Valor real: $y = 1$.
Passo 1: Cálculo de $\delta_1^{(2)}$
Para entropia cruzada + sigmóide, o erro na saída é:
\[\delta_1^{(2)} = \vert{y} - y = 0.5824 - 1 = -0.4176\]Passo 2: Cálculo do Gradiente
Usando a fórmula:
\[\frac{\partial L}{\partial w_{12}^{(2)} } = \delta_1^{(2)} \cdot a_2^{(1)}\]Substituindo os valores:
\[\frac{\partial L}{\partial w_{12}^{(2)} } = (-0.4176) \times 0.3430 \approx -0.1432\]Passo 3: Atualização do Peso
Supondo uma taxa de aprendizado $\eta = 0.01$:
\[w_{12}^{(2)} \leftarrow w_{12}^{(2)} - \eta \frac{\partial L}{\partial w_{12}^{(2)} }\] \[w_{12}^{(2)} \leftarrow -0.3 - 0.01 \times (-0.1432) = -0.3 + 0.001432 = -0.298568\]A atenta leitora deve tomar nota dos seguintes pontos importantes:
-
Simplificação para Entropia Cruzada + Sigmóide: a combinação dessas funções elimina a necessidade de calcular explicitamente $\sigma’(z^{(2)})$, pois a derivada se cancela na regra da cadeia. Isso acelera computacionalmente o treinamento diminuindo o custo total do treinamento.
-
Generalização para Outras Funções: se a função de custo fosse MSE (Erro Quadrático Médio) ou a ativação fosse outra (por exemplo: $\text{ReLU}$), o cálculo de $\delta$ incluiria a derivada da função de ativação:
\[\delta_j^{(l)} = \left(\sum_{k} \delta_k^{(l+1)} w_{kj}^{(l+1)}\right) f'(z_j^{(l)})\]
Implementação do Treinamento
Este é o momento em que a esforçada leitora deve dar uma parada, tomar uma água, ver o céu azul e respirar fundo porque vamos explorar detalhadamente como o treinamento funciona em uma rede neural rasa, semelhante à utilizada nos modelos de word embeddings. Este exemplo detalhado servirá como base para que a encantada leitora domine o processo de treinamento desses modelos.
O processo começa com a inicialização aleatória dos pesos e vieses:
- $W1 = pequenos_valores_aleatorios(tamanho_entrada, tamanho_oculta)$;
- $b1 = zeros(tamanho_oculta)$;
- $W2 = pequenos_valores_aleatorios(tamanho_oculta, tamanho_saida)$;
- $b2 = zeros(tamanho_saida)$.
Passo a Passo da Propagação Direta e Retropropagação
Considere uma rede neural simples com uma camada oculta e uma função de ativação sigmóide. O treinamento de um único exemplo envolve:
-
Propagação direta:
Calculando a saída da camada oculta:
\[h = \sigma(W_1 x + b_1)\]Calculando a saída da rede:
\[\vert{y} = \text{softmax}(W_2 h + b_2)\] -
Cálculo do erro:
\[L = -\sum_{i} y_i \log(\vert{y}_i)\] -
Retropropagação:
Erro na camada de saída:
\[\delta^{(2)} = \vert{y} - y\]Gradientes para $W_2$ e $b_2$:
\[\frac{\partial L}{\partial W^{(2)} } = h^T \delta^{(2)}\]
\[\frac{\partial L}{\partial b_2} = \delta^{(2)}\]Em notação matricial:
- Se $h$ é um vetor linha (dimensão $1 \times d$)
- e $\delta^{(2)}$ é um vetor linha (dimensão $1 \times \vert V \vert $),
a multiplicação correta para gerar um gradiente de dimensão $d \times \vert V \vert $ (compatível com $W^{(2)}$) será:
\[\frac{\partial L}{\partial W^{(2)} } = \underbrace{h^T}_{d \times 1} \underbrace{\delta^{(2)} }_{1 \times \vert V \vert }\]Erro propagado para a camada oculta:
\[\delta^{(1)} = (W_2^T \delta^{(2)}) \odot \sigma'(W_1 x + b_1)\]Gradientes para W1 e b1:
\[\frac{\partial L}{\partial W_1} = \delta^{(1)} x^T\] \[\frac{\partial L}{\partial b_1} = \delta^{(1)}\] -
Atualização dos pesos:
\[W_2 = W_2 - \eta \frac{\partial L}{\partial W_2}\] \[b_2 = b_2 - \eta \frac{\partial L}{\partial b_2}\] \[W_1 = W_1 - \eta \frac{\partial L}{\partial W_1}\] \[b_1 = b_1 - \eta \frac{\partial L}{\partial b_1}\]
Otimizações do Treinamento
Na prática, várias otimizações são aplicadas para melhorar a eficiência e eficácia do treinamento:
Gradient Descent com Mini-lotes (Mini-batch Gradient Descent)
Em vez de atualizar os parâmetros após cada exemplo (o que é chamado de Gradiente Descendente Estocástico ou SGD) ou usar todos os exemplos do conjunto de treinamento de uma vez (Gradiente Descendente Batch ou GD), uma abordagem comum é usar pequenos lotes (mini-batches) de exemplos. Isso oferece um equilíbrio entre a velocidade de convergência e a estabilidade do processo de treinamento. A atualização para todos os parâmetros $\theta$ da rede (pesos e vieses) usando um mini-lote de tamanho $m$ é dada por:
\[\theta \leftarrow \theta - \eta \frac{1}{m} \sum_{i=1}^{m} \nabla_{\theta} L^{(i)}\]Neste caso:
- $\theta$ representa o vetor de todos os parâmetros ajustáveis da rede.
- $m$ representa o tamanho do mini-lote.
- $L^{(i)}$ é a função de custo calculada para o $i$-ésimo exemplo do mini-lote.
- $\nabla_{\theta} L^{(i)}$ é o vetor de gradientes da função de custo em relação a todos os parâmetros $\theta$, calculado para o exemplo $i$. A soma calcula o gradiente médio sobre o mini-lote.
Taxa de Aprendizado Adaptativa
A taxa de aprendizado $\eta$ pode diminuir ao longo do tempo para permitir convergência mais precisa:
\[\eta_t = \eta_0 \cdot (1 - \frac{t}{T})\]Onde $t$ é a iteração atual e $T$ é o número total de iterações.
Algoritmos como Adam, RMSprop e Adagrad ajustam a taxa de aprendizado individualmente para cada parâmetro baseado no histórico de gradientes.
Regularização L2
Antes de detalharmos técnicas como regularização, é importante entender dois desafios comuns no treinamento de redes neurais: Overfitting e Underfitting.
-
Underfitting (Subajuste): ocorre quando o modelo é muito simples para capturar os padrões presentes nos dados de treinamento. Ele falha em aprender bem tanto nos dados de treino quanto em dados novos. Isso geralmente indica que a arquitetura da rede é inadequada ou que o treinamento foi insuficiente.
-
Overfitting (Sobreajuste): ocorre quando o modelo aprende os dados de treinamento excessivamente bem, incluindo ruídos e particularidades específicas daquele conjunto de dados. Como resultado, o modelo tem um desempenho excelente nos dados de treino, mas generaliza mal para dados novos e não vistos, apresentando um erro muito maior nesses casos. O modelo “decorou” o treino em vez de aprender os padrões gerais.
O objetivo do treinamento é encontrar um equilíbrio, um modelo que generalize bem para novos dados. As técnicas de otimização e, especialmente, de regularização, são projetadas principalmente para combater o overfitting.
L2 Regularization (Regularização L2): adiciona um termo à função de custo que penaliza pesos grandes:
\[L_{reg} = L + \frac{\lambda}{2} \sum_w w^2\]A regularização L2 adiciona um termo de penalidade à função de custo original ($L$) para desencorajar pesos muito grandes, ajudando a prevenir o overfitting. A fórmula é:
\[L_{reg} = L + \frac{\lambda}{2} \sum_{k} w_k^2\]Em que $\lambda$ é o hiperparâmetro de força da regularização e a soma é sobre todos os pesos $w_k$ na rede, ou em uma camada específica.
Exemplo: suponha que uma camada da rede tem os seguintes pesos:
\[w = [0.5, -0.2, 1.0, -1.5]\]E escolhemos uma força de regularização $\lambda = 0.01$.
Passo 1: Calcular a soma dos quadrados dos pesos.
\[\sum_{k} w_k^2 = (0.5)^2 + (-0.2)^2 + (1.0)^2 + (-1.5)^2\] \[\sum_{k} w_k^2 = 0.25 + 0.04 + 1.0 + 2.25 = 3.54\]Passo 2: Calcular o termo de penalidade L2.
\[\text{Penalidade L2} = \frac{\lambda}{2} \sum_{k} w_k^2 = \frac{0.01}{2} \times 3.54\] \[\text{Penalidade L2} = 0.005 \times 3.54 = 0.0177\]Passo 3: Adicionar a penalidade ao custo original.
Se o custo calculado a partir do erro de previsão (por exemplo:, entropia cruzada) fosse $L = 0.3567$, o custo regularizado seria:
\[L_{reg} = L + \text{Penalidade L2} = 0.3567 + 0.0177 = 0.3744\]É este valor $L_{reg}$ que o algoritmo de otimização tentará minimizar. A penalidade adicional puxa os pesos para valores menores durante o treinamento.
Dropout como Alternativa de Regularização
Além da regularização L2, uma técnica de regularização extremamente eficaz para redes neurais é o Dropout, que pode ser traduzido como abandono, proposto por Hinton et al. em 2012. Diferentemente da regularização L2 que opera modificando a função de custo, o Dropout atua diretamente na arquitetura da rede durante o treinamento. O Dropout consiste em desativar aleatoriamente uma fração dos neurônio durante cada passo do treinamento. Matematicamente, para cada exemplo de treinamento e iteração, uma máscara aleatória $m$ é gerada, onde cada elemento $m_j$ segue uma distribuição de Bernoulli:
\[m_j \sim \text{Bernoulli}(p)\]Na qual, $p$ é a probabilidade de manter um neurônio ativo, tipicamente entre $0.5$ e $0.8$. Durante a propagação direta, a ativação de uma camada com Dropout será calculada por:
\[\tilde{h} = m \odot h\]Neste caso, $\odot$ representa a multiplicação elemento a elemento, $h$ é o vetor de ativações original e $\tilde{h}$ é o vetor de ativações com Dropout aplicado. Na prática, o Dropout pode ser visto como treinar um conjunto de diferentes sub-redes a cada iteração.
O Dropout combate o overfitting por meio dos seguintes mecanismos:
- Prevenção de co-adaptação: os neurônios não podem depender excessivamente uns dos outros, pois qualquer neurônio pode ser desativado a qualquer momento.
- Efeito de ensemble (conjunto): o Dropout efetivamente treina um grande número de redes diferentes com pesos compartilhados, que são então implicitamente combinadas durante a inferência.
- Adição de ruído: adiciona uma forma de ruído controlado durante o treinamento, forçando a rede a aprender representações mais robustas.
Matematicamente, pode-se mostrar que o Dropout aproxima um tipo de regularização adaptativa, onde a penalidade aplicada a cada peso varia de acordo com a sua importância.
Implementação no Treinamento e Inferência: durante o treinamento, o Dropout é aplicado a cada camada da rede, exceto na camada de saída. Durante a inferência, não aplicamos o Dropout, mas escalamos as ativações para compensar a fração de neurônios que foram desativados durante o treinamento. Assim:
Durante o treinamento: para cada exemplo do mini-lote:
- Gerar uma máscara binária $m$ com probabilidade $p$ de $1$’s;
- Multiplicar as ativações pela máscara: $\tilde{h} = m \odot h$;
- Prosseguir com a propagação direta e retropropagação normalmente.
Durante a inferência (teste): não aplicamos o Dropout diretamente. Em vez disso, escalamos as ativações dos neurônios por $p$ para compensar o fato de que durante o treinamento, em média, apenas uma fração $p$ dos neurônios estava ativa. Alternativamente, podemos escalar os pesos durante a inferência por um fator de $p$, o que tem o mesmo efeito.
A esforçada leitora deve observar que o Dropout é aplicado apenas durante o treinamento, e não durante a inferência. Durante a inferência, todos os neurônios estão ativos, mas as ativações são escaladas para refletir a fração de neurônios que estavam ativos durante o treinamento. Finalmente, podemos ver um exemplo de dropout.
Considere uma camada oculta com $4$ neurônios cuja ativação para um determinado exemplo seja:
\[h = [0.6, 0.2, 0.8, 0.4]\]Com uma taxa de Dropout $p = 0.75$. isso significa que serão mantidos $75\%$ dos neurônios ativos. Geramos uma máscara aleatória:
\[m = [1, 0, 1, 1]\]Aplicando o Dropout:
\[\tilde{h} = m \odot h = [0.6, 0, 0.8, 0.4]\]A atenta leitora deve observar que o segundo neurônio foi desativado para esta iteração. A propagação direta e a retropropagação prosseguem utilizando $\tilde{h}$ em vez de $h$. Sendo assim, durante a inferência, teríamos duas opções:
- Usar todos os neurônios sem Dropout e escalar as ativações: $h_{\text{teste} } = p \cdot h = 0.75 \cdot [0.6, 0.2, 0.8, 0.4] = [0.45, 0.15, 0.6, 0.3]$;
- Ou, equivalentemente, escalar os pesos da camada por $p$.
Comparação entre Regularização L2 e Dropout
| Aspecto | Regularização L2 | Dropout |
|---|---|---|
| Princípio Básico | Penaliza pesos grandes na função de custo | Desativa aleatoriamente neurônios durante o treinamento |
| Implementação | Adiciona termo $\frac{\lambda}{2}\sum w^2$ à função de custo | Multiplica ativações por máscara binária aleatória |
| Hiperparâmetros | $\lambda$ (força da regularização) | $p$ (probabilidade de manter neurônio ativo) |
| Efeito nos Pesos | Puxa todos os pesos em direção a zero | Não afeta diretamente os valores dos pesos |
| Ajuste na Inferência | Nenhum necessário | Escalar ativações ou pesos por $p$ |
| Eficácia em Redes Grandes | Boa, mas pode ser insuficiente sozinha | Excelente, especialmente em redes profundas |
| Custo Computacional | Baixo (apenas termo adicional no custo) | Moderado (geração de máscaras e multiplicações) |
| Situações Ideais | Datasets menores, redes simples | Redes grandes, datasets com ruído |
| Combinação com Outras Técnicas | Combina bem com Dropout | Pode ser usado com L1/L2 para maior regularização |
| Efeito em Word Embeddings | Pode comprimir os embeddings no espaço | Pode criar embeddings mais diversos e robustos |
Na prática, frequentemente ambas as técnicas são utilizadas em conjunto para obter o melhor dos dois mundos: o Dropout previne a co-adaptação de neurônios, enquanto a regularização L2 mantém os pesos em valores razoáveis.
Exemplo Completo de Treinamento de uma Rede Neural Rasa
Neste exemplo, a esforçada leitora poderá ver, cuidadosamente, como treinar uma rede neural rasa para prever uma palavra com base em outra, utilizando um vocabulário pequeno e realizando todos os cálculos passo a passo. O objetivo é ilustrar os conceitos de propagação direta, cálculo do custo, retropropagação e atualização dos pesos, que são fundamentais para entender algoritmos como CBOW e SkipGram que serão assunto deste artigo.
Definição da Rede
- Vocabulário: {“sol”, “lua”, “dia”, “noite”} (tamanho $ \vert V \vert = 4 $);
- Camada de Entrada: Vetor One-Hot de tamanho $4$, representando uma palavra de entrada;
- Camada Oculta: $2$ neurônios, projeção linear, sem função de ativação;
- Camada de Saída: $4$ neurônios, probabilidades para cada palavra do vocabulário, usando softmax.
Inicialização dos Pesos
Inicializamos as matrizes de pesos com valores fixos para facilitar os cálculos:
- Pesos da Camada Oculta ($W^{(1)}$), matriz $4 \times 2$:
- Pesos da Camada de Saída ($W^{(2)}$), matriz $ 2 \times 4 $:
- Não usaremos vieses ($b = 0$).
Entrada e Saída Esperada
- Entrada: palavra “sol”, vetor One-Hot $ x = [1, 0, 0, 0] $;
- Saída Esperada: palavra “dia”, vetor One-Hot $ y = [0, 0, 1, 0]$.
Propagação Direta
Passo 1: calcular a Ativação da Camada Oculta
A ativação da camada oculta $h$ será obtida multiplicando a entrada $x$ pelos pesos $W^{(1)}$:
\[h = x \cdot W^{(1)} = [1, 0, 0, 0] \cdot \begin{pmatrix} 0.1 & 0.2 \\ 0.3 & 0.4 \\ 0.5 & 0.6 \\ 0.7 & 0.8 \end{pmatrix}\]Como $x$ é um vetor One-Hot com $1$ na primeira posição, $h$ corresponde à primeira linha de $W^{(1)}$:
\[h = [0.1, 0.2]\]Passo 2: Calcular a Ativação da Camada de Saída
-
Cálculo do Vetor de Pontuações ($z$)
Multiplicamos $h$ pelos pesos $W^{(2)}$:
\[z = h \cdot W^{(2)} = [0.1, 0.2] \cdot \begin{pmatrix} 0.2 & 0.3 & 0.4 & 0.5 \\ 0.6 & 0.7 & 0.8 & 0.9 \end{pmatrix}\]Calculando cada componente:
\[z_1 = 0.1 \cdot 0.2 + 0.2 \cdot 0.6 = 0.02 + 0.12 = 0.14\] \[z_2 = 0.1 \cdot 0.3 + 0.2 \cdot 0.7 = 0.03 + 0.14 = 0.17\] \[z_3 = 0.1 \cdot 0.4 + 0.2 \cdot 0.8 = 0.04 + 0.16 = 0.20\] \[z_4 = 0.1 \cdot 0.5 + 0.2 \cdot 0.9 = 0.05 + 0.18 = 0.23\]Portanto:
\[z = [0.14, 0.17, 0.20, 0.23]\] -
Aplicação da Função Softmax
A saída prevista $ \vert{y}$ é calculada com a função softmax:
\[\vert{y}_i = \frac{e^{z_i} }{\sum_{j=1}^{4} e^{z_j} }\]Calculando os exponenciais (aproximados):
\[e^{0.14} \approx 1.150, \quad e^{0.17} \approx 1.185, \quad e^{0.20} \approx 1.221, \quad e^{0.23} \approx 1.259\]Soma dos exponenciais:
\[1.150 + 1.185 + 1.221 + 1.259 = 4.815\]Agora, calculamos cada $\vert{y}_i$:
\[\vert{y}_1 = \frac{1.150}{4.815} \approx 0.239\] \[\vert{y}_2 = \frac{1.185}{4.815} \approx 0.246\] \[\vert{y}_3 = \frac{1.221}{4.815} \approx 0.254\] \[\vert{y}_4 = \frac{1.259}{4.815} \approx 0.261\]Portanto:
\[\vert{y} = [0.239, 0.246, 0.254, 0.261]\] -
Cálculo do Custo
Usamos a entropia cruzada como função de custo:
\[L = -\sum_{i=1}^{4} y_i \log(\vert{y}_i)\]Como $y = [0, 0, 1, 0]$, apenas o terceiro termo contribui:
\[L = - y_3 \log(\vert{y}_3) = - 1 \cdot \log(0.254)\]Calculando:
\[\log(0.254) \approx -1.370\] \[L = -(-1.370) = 1.370\]
Retropropagação
Passo 1: calcular o Erro na Camada de Saída Para softmax com entropia cruzada, o erro $\delta^{(2)}$ será:
\[\delta^{(2)} = \vert{y} - y\] \[\delta^{(2)} = [0.239, 0.246, 0.254, 0.261] - [0, 0, 1, 0]\] \[\delta^{(2)} = [0.239, 0.246, 0.254 - 1, 0.261] = [0.239, 0.246, -0.746, 0.261]\]Passo 2: calcular os Gradientes para $W^{(2)}$ O gradiente do custo em relação a $W^{(2)}$ é:
\[\frac{\partial L}{\partial W^{(2)} } = h^T \cdot \delta^{(2)}\]Com $h = [0.1, 0.2]$, vetor coluna $h^T = \begin{pmatrix} 0.1 \ 0.2 \end{pmatrix}$:
\[\frac{\partial L}{\partial W^{(2)} } = \begin{pmatrix} 0.1 \\ 0.2 \end{pmatrix} \cdot [0.239, 0.246, -0.746, 0.261]\]Calculando cada elemento:
\[\frac{\partial L}{\partial W^{(2)} } = \begin{pmatrix} 0.1 \cdot 0.239 & 0.1 \cdot 0.246 & 0.1 \cdot (-0.746) & 0.1 \cdot 0.261 \\ 0.2 \cdot 0.239 & 0.2 \cdot 0.246 & 0.2 \cdot (-0.746) & 0.2 \cdot 0.261 \end{pmatrix}\] \[\approx \begin{pmatrix} 0.0239 & 0.0246 & -0.0746 & 0.0261 \\ 0.0478 & 0.0492 & -0.1492 & 0.0522 \end{pmatrix}\]Passo 3: propagar o Erro para a Camada Oculta. O erro $\delta^{(1)}$ na camada oculta é:
\[\delta^{(1)} = \delta^{(2)} \cdot (W^{(2)})^T\]Transposta de $W^{(2)}$:
\[(W^{(2)})^T = \begin{pmatrix} 0.2 & 0.6 \\ 0.3 & 0.7 \\ 0.4 & 0.8 \\ 0.5 & 0.9 \end{pmatrix}\]Calculando:
\[\delta^{(1)} = [0.239, 0.246, -0.746, 0.261] \cdot \begin{pmatrix} 0.2 & 0.6 \\ 0.3 & 0.7 \\ 0.4 & 0.8 \\ 0.5 & 0.9 \end{pmatrix}\]Para cada componente:
\[\delta^{(1)}_1 = 0.239 \cdot 0.2 + 0.246 \cdot 0.3 + (-0.746) \cdot 0.4 + 0.261 \cdot 0.5\] \[= 0.0478 + 0.0738 - 0.2984 + 0.1305 \approx -0.0463\] \[\delta^{(1)}_2 = 0.239 \cdot 0.6 + 0.246 \cdot 0.7 + (-0.746) \cdot 0.8 + 0.261 \cdot 0.9\] \[= 0.1434 + 0.1722 - 0.5968 + 0.2349 \approx -0.0463\]Portanto:
\[\delta^{(1)} = [-0.0463, -0.0463]\]Passo 4: calcular os Gradientes para $W^{(1)}$. O gradiente do custo em relação a $W^{(1)}$ é:
\[\frac{\partial L}{\partial W^{(1)} } = x^T \cdot \delta^{(1)}\]Com $x = [1, 0, 0, 0]$, vetor coluna $x^T = \begin{pmatrix} 1 \ 0 \ 0 \ 0 \end{pmatrix}$:
\[\frac{\partial L}{\partial W^{(1)} } = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \cdot [-0.0463, -0.0463]\] \[= \begin{pmatrix} 1 \cdot (-0.0463) & 1 \cdot (-0.0463) \\ 0 \cdot (-0.0463) & 0 \cdot (-0.0463) \\ 0 \cdot (-0.0463) & 0 \cdot (-0.0463) \\ 0 \cdot (-0.0463) & 0 \cdot (-0.0463) \end{pmatrix}\] \[= \begin{pmatrix} -0.0463 & -0.0463 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{pmatrix}\]Atualização dos Pesos
Usamos uma taxa de aprendizado $\eta = 0.1$.
-
Atualização de $W^{(2)}$
\[W^{(2)} \leftarrow W^{(2)} - \eta \cdot \frac{\partial L}{\partial W^{(2)} }\] \[W^{(2)} = \begin{pmatrix} 0.2 & 0.3 & 0.4 & 0.5 \\ 0.6 & 0.7 & 0.8 & 0.9 \end{pmatrix} - 0.1 \cdot \begin{pmatrix} 0.0239 & 0.0246 & -0.0746 & 0.0261 \\ 0.0478 & 0.0492 & -0.1492 & 0.0522 \end{pmatrix}\]Calculando cada elemento:
\[W^{(2)}_{1,1} = 0.2 - 0.1 \cdot 0.0239 = 0.2 - 0.00239 \approx 0.1976\] \[W^{(2)}_{1,2} = 0.3 - 0.1 \cdot 0.0246 = 0.3 - 0.00246 \approx 0.2975\] \[W^{(2)}_{1,3} = 0.4 - 0.1 \cdot (-0.0746) = 0.4 + 0.00746 \approx 0.4075\] \[W^{(2)}_{1,4} = 0.5 - 0.1 \cdot 0.0261 = 0.5 - 0.00261 \approx 0.4974\] \[W^{(2)}_{2,1} = 0.6 - 0.1 \cdot 0.0478 = 0.6 - 0.00478 \approx 0.5952\] \[W^{(2)}_{2,2} = 0.7 - 0.1 \cdot 0.0492 = 0.7 - 0.00492 \approx 0.6951\] \[W^{(2)}_{2,3} = 0.8 - 0.1 \cdot (-0.1492) = 0.8 + 0.01492 \approx 0.8149\] \[W^{(2)}_{2,4} = 0.9 - 0.1 \cdot 0.0522 = 0.9 - 0.00522 \approx 0.8948\]Nova matriz $W^{(2)}$:
\[W^{(2)} \approx \begin{pmatrix} 0.1976 & 0.2975 & 0.4075 & 0.4974 \\ 0.5952 & 0.6951 & 0.8149 & 0.8948 \end{pmatrix}\] -
Atualização de $W^{(1)}$
\[W^{(1)} \leftarrow W^{(1)} - \eta \cdot \frac{\partial L}{\partial W^{(1)} }\] \[W^{(1)} = \begin{pmatrix} 0.1 & 0.2 \\ 0.3 & 0.4 \\ 0.5 & 0.6 \\ 0.7 & 0.8 \end{pmatrix} - 0.1 \cdot \begin{pmatrix} -0.0463 & -0.0463 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{pmatrix}\]Calculando:
\[W^{(1)}_{1,1} = 0.1 - 0.1 \cdot (-0.0463) = 0.1 + 0.00463 \approx 0.1046\] \[W^{(1)}_{1,2} = 0.2 - 0.1 \cdot (-0.0463) = 0.2 + 0.00463 \approx 0.2046\]As outras linhas permanecem inalteradas (gradiente zero):
\[W^{(1)} = \begin{pmatrix} 0.1046 & 0.2046 \\ 0.3 & 0.4 \\ 0.5 & 0.6 \\ 0.7 & 0.8 \end{pmatrix}\]
Neste exemplo, a estupefata leitora pode ver como treinar uma rede neural rasa para prever dia a partir de sol. O processo incluiu propagação direta, cálculo do custo com entropia cruzada, retropropagação para determinar os gradientes e atualização dos pesos com uma taxa de aprendizado. Este exemplo serve como base para entender modelos de word embeddings como CBOW e Skip-gram, ajustando apenas as entradas e saídas conforme necessário. A rede pode ser vista na Figura 8.
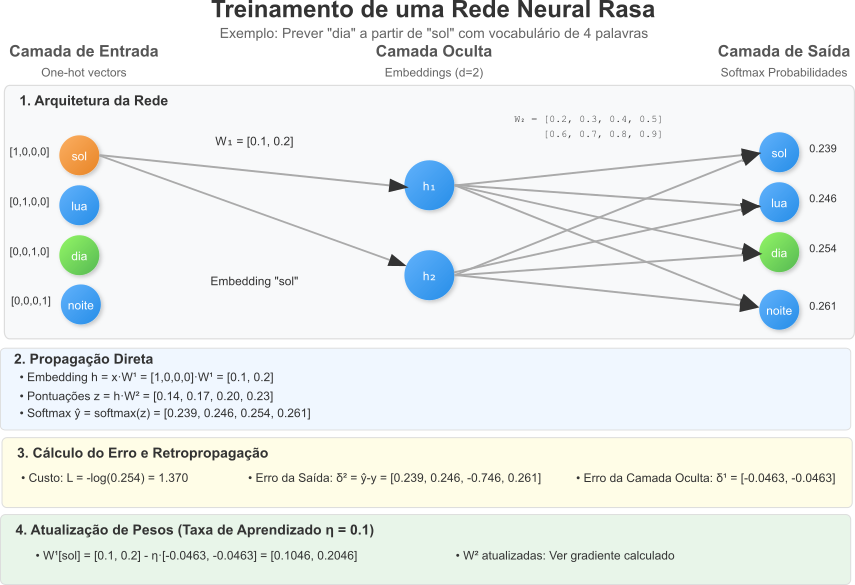
Figura 7: Esquema da Rede Rasa treinada no exemplo.
Implementação em C++ 20 do Exemplo de Treinamento de uma Rede Neural Rasa
#include <iostream> /**< Para operações de entrada/saída padrão */
#include <vector> /**< Para std::vector, usado para armazenar pesos e ativações */
#include <cmath> /**< Para funções matemáticas como std::exp e std::log */
#include <iomanip> /**< Para formatação de saída numérica */
/**
* @brief Calcula o produto escalar de dois vetores
* @param a Primeiro vetor de entrada
* @param b Segundo vetor de entrada
* @return Valor do produto escalar entre os vetores
*/
float dot(const std::vector<float>& a, const std::vector<float>& b) {
float result = 0.0f;
for (size_t i = 0; i < a.size(); ++i) {
result += a[i] * b[i];
}
return result;
}
/**
* @brief Calcula o softmax de um vetor de scores
* @param scores Vetor de pontuações de entrada
* @return Vetor de probabilidades após aplicação do softmax
* @details Implementa estabilidade numérica subtraindo o valor máximo
* antes de calcular as exponenciais
*/
std::vector<float> softmax(const std::vector<float>& scores) {
std::vector<float> exps(scores.size());
float max_score = *std::max_element(scores.begin(), scores.end());
float sum_exps = 0.0f;
for (size_t i = 0; i < scores.size(); ++i) {
exps[i] = std::exp(scores[i] - max_score); // Subtrai max para estabilidade numérica
sum_exps += exps[i];
}
for (float& val : exps) {
val /= sum_exps;
}
return exps;
}
/**
* @brief Função principal que implementa o exemplo de treinamento da rede neural rasa
* @return 0 se a execução for bem-sucedida
*/
int main() {
// --- Definir Vocabulário e Índices ---
/**
* @brief Vocabulário e configuração da rede
* Vocabulário: {"sol", "lua", "dia", "noite"} com índices {0, 1, 2, 3}
*/
int vocab_size = 4;
int vector_size = 2; /**< Dimensão da camada oculta */
// --- Definir Pesos de Entrada e Saída ---
/**
* @brief Matriz de pesos da camada de entrada W^(1)
* Formato: matriz 4x2 conforme definido no exemplo
*/
std::vector<std::vector<float>> W_input = {
{0.1, 0.2}, // "sol"
{0.3, 0.4}, // "lua"
{0.5, 0.6}, // "dia"
{0.7, 0.8} // "noite"
};
/**
* @brief Matriz de pesos da camada de saída W^(2)
* Formato: matriz 2x4 conforme definido no exemplo
*/
std::vector<std::vector<float>> W_output = {
{0.2, 0.3, 0.4, 0.5},
{0.6, 0.7, 0.8, 0.9}
};
// --- Definir Par de Treinamento ---
/**
* @brief Definição da entrada e saída esperada
* Entrada: palavra "sol" (índice 0), representada como vetor one-hot [1,0,0,0]
* Saída esperada: palavra "dia" (índice 2), representada como vetor one-hot [0,0,1,0]
*/
int input_idx = 0; // "sol"
int target_idx = 2; // "dia"
float learning_rate = 0.1f; /**< Taxa de aprendizado (η) */
// --- Passo 1: Calcular a Ativação da Camada Oculta ---
/**
* @brief Calcula a ativação da camada oculta h = x·W^(1)
* Como x é um vetor one-hot com 1 na posição input_idx, h é igual
* à linha input_idx da matriz W_input
*/
std::vector<float> h = W_input[input_idx];
// h = [0.1, 0.2] para "sol"
// --- Passo 2: Calcular o Vetor de Pontuações ---
/**
* @brief Calcula o vetor de pontuações z = h·W^(2)
*/
std::vector<float> z(vocab_size, 0.0f);
for (int i = 0; i < vocab_size; ++i) {
for (int j = 0; j < vector_size; ++j) {
z[i] += h[j] * W_output[j][i];
}
}
// z = [0.14, 0.17, 0.20, 0.23]
// --- Passo 3: Aplicar Softmax ---
/**
* @brief Aplica a função softmax para obter as probabilidades previstas
*/
std::vector<float> y_pred = softmax(z);
// y_pred ≈ [0.239, 0.246, 0.254, 0.261]
// --- Passo 4: Calcular a Perda (Entropia Cruzada) ---
/**
* @brief Calcula a função de custo usando entropia cruzada
* L = -∑ y_i·log(y_pred_i), onde y é o vetor one-hot da saída esperada
*/
float loss = -std::log(y_pred[target_idx]);
// loss ≈ 1.370
// --- Passo 5: Calcular o Erro na Camada de Saída ---
/**
* @brief Calcula o erro na camada de saída δ^(2) = y_pred - y
* Onde y é o vetor one-hot da saída esperada
*/
std::vector<float> delta_output(vocab_size, 0.0f);
for (int i = 0; i < vocab_size; ++i) {
delta_output[i] = y_pred[i] - (i == target_idx ? 1.0f : 0.0f);
}
// delta_output ≈ [0.239, 0.246, -0.746, 0.261]
// --- Passo 6: Calcular os Gradientes para W^(2) ---
/**
* @brief Calcula o gradiente da função de custo em relação a W^(2)
* ∂L/∂W^(2) = h^T·δ^(2)
*/
std::vector<std::vector<float>> grad_W_output(vector_size, std::vector<float>(vocab_size, 0.0f));
for (int i = 0; i < vector_size; ++i) {
for (int j = 0; j < vocab_size; ++j) {
grad_W_output[i][j] = h[i] * delta_output[j];
}
}
// grad_W_output ≈ [[0.0239, 0.0246, -0.0746, 0.0261], [0.0478, 0.0492, -0.1492, 0.0522]]
// --- Passo 7: Propagar o Erro para a Camada Oculta ---
/**
* @brief Calcula o erro na camada oculta δ^(1) = δ^(2)·(W^(2))^T
*/
std::vector<float> delta_hidden(vector_size, 0.0f);
for (int i = 0; i < vector_size; ++i) {
for (int j = 0; j < vocab_size; ++j) {
delta_hidden[i] += delta_output[j] * W_output[i][j];
}
}
// delta_hidden ≈ [-0.0463, -0.0463]
// --- Passo 8: Calcular os Gradientes para W^(1) ---
/**
* @brief Calcula o gradiente da função de custo em relação a W^(1)
* ∂L/∂W^(1) = x^T·δ^(1)
* Como x é um vetor one-hot, apenas a linha input_idx será atualizada
*/
std::vector<std::vector<float>> grad_W_input(vocab_size, std::vector<float>(vector_size, 0.0f));
for (int j = 0; j < vector_size; ++j) {
grad_W_input[input_idx][j] = delta_hidden[j];
}
// grad_W_input[0] ≈ [-0.0463, -0.0463], outras linhas são zeros
// --- Passo 9: Atualizar os Pesos ---
/**
* @brief Atualiza os pesos usando gradiente descendente
* W^(new) = W^(old) - η·∂L/∂W
*/
// Atualizar W^(2)
for (int i = 0; i < vector_size; ++i) {
for (int j = 0; j < vocab_size; ++j) {
W_output[i][j] -= learning_rate * grad_W_output[i][j];
}
}
// Atualizar W^(1)
for (int i = 0; i < vocab_size; ++i) {
for (int j = 0; j < vector_size; ++j) {
W_input[i][j] -= learning_rate * grad_W_input[i][j];
}
}
// --- Exibir Resultados ---
/**
* @brief Exibe os resultados dos cálculos e pesos atualizados
*/
std::cout << std::fixed << std::setprecision(4);
std::cout << "Ativação da Camada Oculta (h): ";
for (float val : h) std::cout << val << " ";
std::cout << "\n";
std::cout << "Vetor de Pontuações (z): ";
for (float val : z) std::cout << val << " ";
std::cout << "\n";
std::cout << "Probabilidades Previstas (ŷ): ";
for (float val : y_pred) std::cout << val << " ";
std::cout << "\n";
std::cout << "Função de Custo (L): " << loss << "\n";
std::cout << "Erro na Camada de Saída (δ^(2)): ";
for (float val : delta_output) std::cout << val << " ";
std::cout << "\n";
std::cout << "Erro na Camada Oculta (δ^(1)): ";
for (float val : delta_hidden) std::cout << val << " ";
std::cout << "\n";
std::cout << "W^(1) Atualizado para 'sol' (índice 0): ";
for (float val : W_input[0]) std::cout << val << " ";
std::cout << "\n";
std::cout << "W^(2) Atualizado: \n";
for (int i = 0; i < vector_size; ++i) {
std::cout << " Linha " << i << ": ";
for (float val : W_output[i]) std::cout << val << " ";
std::cout << "\n";
}
return 0;
}
Aplicações em word embeddings
Agora que entendemos os fundamentos das redes neurais rasas, podemos compreender como os modelos de word embeddings utilizam essa arquitetura para aprender representações distribuídas de palavras. A atenta leitora deve lembrar que os word embeddings são representações vetoriais densas de palavras, onde palavras semanticamente semelhantes estão próximas no espaço vetorial e são a base teórica sobre a qual construímos os modelos transformers.
No coração dos modelos de word embeddings está a camada de projeção, que é essencialmente a camada oculta da rede neural:
A matriz de pesos $W$ entre a camada de entrada e a camada oculta tem dimensões $ \vert V \vert \times d$, onde $ \vert V \vert $ é o tamanho do vocabulário e $d$ é a dimensão do embedding. Após o treinamento, cada linha dessa matriz representa o embedding de uma palavra específica.
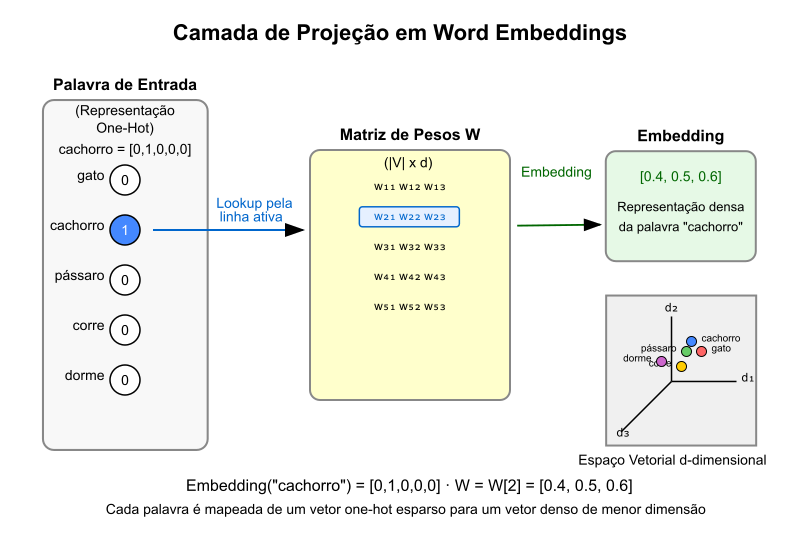
Figura 8: Ilustração detalhada da camada de projeção em modelos de word embeddings. À esquerda, a representação one-hot da palavra cachorro no vocabulário. Ao centro, a matriz de pesos $W$, dimensões $\vert V \vert \times d$, que mapeia as palavras para o espaço vetorial denso. À direita, o vetor de embedding resultante após a operação de consulta, *lookup, em inglês* na linha correspondente da matriz. O espaço vetorial d-dimensional mostra como diferentes palavras são posicionadas de acordo com suas relações semânticas.
Do ponto de vista da álgebra linear, esta matriz de pesos $W$ representa uma transformação linear do espaço One-Hot de dimensão $ \vert V \vert $ para o espaço de embedding denso de dimensão $d$. O processo de treinamento visa aprender os elementos dessa matriz $W$ de forma que a transformação capture as relações semânticas desejadas.
A camada de projeção nos modelos de word embeddings funciona como uma tabela de consulta eficiente, onde a matriz de pesos $W$ armazena os vetores de embedding. Considere um vocabulário minúsculo: $V = {\text{“a”}, \text{“b”}, \text{“c”}, \text{“d”}}$ tal que: $\vert V \vert =4$. Neste caso, queremos aprender embeddings de dimensão $d=3$.
A matriz de pesos $W$, também chamada de matriz de embedding, terá dimensões $\vert V \vert \times d$, ou seja, $4 \times 3$. Cada linha corresponde ao vetor de embedding de uma palavra do vocabulário. Vamos supor que a matriz $W$ seja:
\[W = \begin{pmatrix} 0.1 & 0.2 & 0.3 \\ % Embedding de a (linha 1) 0.4 & 0.5 & 0.6 \\ % Embedding de b (linha 2) 0.7 & 0.8 & 0.9 \\ % Embedding de c (linha 3) 1.0 & 1.1 & 1.2 % Embedding de d (linha 4) \end{pmatrix}\]Agora, suponha que a palavra de entrada seja b. Sua representação One-Hot será um vetor $x$ de tamanho $ \vert V \vert =4$, com $1$ na posição correspondente a b, a segunda posição, e $0$ nas demais:
A operação de projeção é matematicamente equivalente a multiplicar o vetor One-Hot $x$, como um vetor linha, pela matriz $W$:
\[\text{Embedding}(\text{"b"}) = x \cdot W = [0, 1, 0, 0] \begin{pmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.6 \\ 0.7 & 0.8 & 0.9 \\ 1.0 & 1.1 & 1.2 \end{pmatrix}\]Calculando a multiplicação:
-
O primeiro elemento do resultado será dado por: $(0 \times 0.1) + (1 \times 0.4) + (0 \times 0.7) + (0 \times 1.0) = 0.4$;
-
O segundo elemento do resultado será dado por: $(0 \times 0.2) + (1 \times 0.5) + (0 \times 0.8) + (0 \times 1.1) = 0.5$;
-
O terceiro elemento do resultado será dado por: $(0 \times 0.3) + (1 \times 0.6) + (0 \times 0.9) + (0 \times 1.2) = 0.6$.
Neste caso o resultado será:
\[\text{Embedding}(\text{`b`}) = [0.4, 0.5, 0.6]\]Observe que este é exatamente a segunda linha da matriz $W$. Na prática, as bibliotecas implementam isso como uma operação de lookup, consulta em inglês, direta na matriz $W$ usando o índice da palavra. Neste caso, índice $1$, assumindo indexação baseada em $0$, ou índice #2# se baseada em 1, o que é muito mais eficiente do que realizar a multiplicação matricial completa. As redes neurais são usadas para treinamento em busca dos valores desta matriz $W$.
Redes Neurais Simplificadas dos Modelos de Embeddings
A arquitetura específica dos modelos de word embeddings pode ser descrita como uma rede neural simplificada. Em sua forma mais básica:
- A camada de entrada recebe representações one-hot das palavras;
- A camada oculta linear (sem função de ativação não-linear) projeta estas representações para um espaço vetorial de menor dimensão;
- A camada de saída, com ativação softmax, produz probabilidades para as palavras a serem previstas.
O que torna esta arquitetura especial é que não estamos interessados na saída da rede (as previsões de palavras), mas sim nos pesos aprendidos. Além disso, a camada oculta não utiliza funções de ativação não-lineares. Finalmente, o objetivo implícito destas redes, neste domínio que estamos estudando, é capturar relações semânticas entre palavras através da co-ocorrência estatística. Esta simplicidade arquitetural é suficiente para aprender representações distribuídas de palavras que capturam de forma surpreendente relações semânticas e sintáticas. Veremos estes conceitos com uma pouco mais de detalhes neste artigo.
Desafios e Otimizações
Os modelos de word embeddings, embora conceitualmente simples, enfrentam desafios práticos na implementação:
Problema de Computação do Softmax: o cálculo do softmax na camada de saída envolve normalizar sobre todo o vocabulário, o que pode ser computacionalmente proibitivo para vocabulários grandes. Observe que o softmax é dado por:
\[p(w_O \vert w_I) = \frac{\exp(v^{'}\_{w_O} \cdot v_{w_I})}{\sum_{w \in V} \exp(v^{'}\_w \cdot v_{w_I})}\]Nesta equação, $v_{w_I}$ é o vetor da palavra de entrada e $v^{‘}_w$ é o vetor de saída associado à palavra $w$. O processo de cálculo e a origem do custo computacional podem ser detalhados da seguinte forma:
- Cálculo dos Scores Brutos: para cada palavra $w$ no vocabulário $V$, calcula-se um score, frequentemente o produto escalar $v^{‘}_w \cdot v_{w_I}\;$;
- Transformação Exponencial: cada score é transformado pela função exponencial, $\exp(v^{‘}_w \cdot v_{w_I})$, garantindo valores positivos;
- Cálculo do Termo de Normalização (Denominador): este é o passo computacionalmente intensivo. É necessário calcular a soma dos scores exponenciais para todas as $\vert V \vert$ palavras no vocabulário: $\sum_{w \in V} \exp(v^{‘}_w \cdot v_{w_I})$;
- Obtenção da Probabilidade (Normalização): a probabilidade final para uma palavra específica $w_O$ é obtida dividindo seu score exponencial pelo termo de normalização (o denominador calculado no passo anterior). Isso garante que $\sum_{w_O \in V} p(w_O \vert w_I) = 1$.
A necessidade de calcular o denominador, somando sobre todas as $\vert V \vert$ palavras do vocabulário para cada exemplo ou atualização, resulta em uma complexidade computacional de $O(\vert V \vert)$, tornando o Softmax padrão impraticável para vocabulários muito grandes e motivando o uso de otimizações como Negative Sampling ou Hierarchical Softmax.
Negative Sampling: Uma técnica que reduz o custo computacional do softmax padrão, amostrando apenas um pequeno número de palavras negativas (incorretas) para cada palavra-alvo. Isso transforma o problema de classificação multiclasse em vários problemas de classificação binária, reduzindo significativamente o custo computacional. Para isso, transformamos o problema de classificação multiclasse em vários problemas de classificação binária, reduzindo significativamente o custo computacional.
A intuitiva leitora pode pensar que, em vez de tentar prever a palavra correta entre todas as palavras do vocabulário, multiclasse, a técnica Negative Sampling treina a rede para distinguir a palavra-alvo real de algumas poucas palavras negativas, no sentido de incorretas, amostradas aleatoriamente. Isso simplifica enormemente o cálculo a cada passo.
A criativa leitora não precisa aceitar minha palavra. Vamos ver um exemplo prático de como isso funciona passo a passo:
Passo 1: vamos criar um cenário inicial considerando o modelo SkipGram com um vocabulário reduzido. Suponha que temos um vocabulário de 7 palavras: $V = {\text{o, gato, preto, corre, pelo, jardim, cachorro}}$.
- Palavra de Entrada (Alvo): $w_I$ =
preto; - Palavra de Contexto (Saída Real/Positiva): $w_O$ =
gato; - Vocabulário (simplificado): $V = {\text{o, gato, preto, corre, pelo, jardim, cachorro}}$ ($\vert V \vert = 7$);
- Dimensão do Embedding: $d = 4$. É um hiperparâmetro do modelo. Escolhi um valor baixo, $4$, para simplificar os cálculos manuais no exemplo. Valores reais comuns são $50$, $100$, $300$, etc.
- Número de Amostras Negativas: $k = 2$. É um hiperparâmetro do modelo. Escolhi $k = 2$ para manter o exemplo conciso. Valores comuns na prática estão entre $5$ e $20$.
- Vetores (Iniciais/Fictícios):
- Vetor de Entrada para
preto($v_{\text{preto} }$): $[0.4, -0.3, 0.1, 0.5]$. Os valores específicos deste vetor são hipotéticos. Em um treinamento real, os vetores são inicializados aleatoriamente, com valores pequenos, e depois aprendidos, ajustados, durante o processo de treinamento. Escolhi alguns valores para permitir o cálculo no exemplo. - Vetores de Saída ($v^{‘}_w$) para algumas palavras. Assim como o vetor de entrada, os valores específicos dos vetores de saída, também chamados de pesos da camada de saída ou context vectors, são hipotéticos. Eles também seriam inicializados aleatoriamente e aprendidos durante o treinamento. Para nosso exemplo, escolhi os seguintes valores:
- $v^{‘}_{\text{gato} }$ (Positivo): $[0.1, 0.2, -0.2, 0.4]$
- $v^{‘}_{\text{cachorro} }$ (Negativo 1): $[0.1, -0.3, 0.8, -0.1]$
- $v^{‘}_{\text{jardim} }$ (Negativo 2): $[0.5, 0.1, 0.3, -0.2]$
- Vetor de Entrada para
Passo 2: processo de Treinamento para o Par (preto, gato) com $k=2$. Nosso objetivo é treinar a rede para:
- aumentar a probabilidade do par positivo (
preto,gato) ser observado; - diminuir a probabilidade dos pares negativos (
preto,cachorro) e (preto,jardim) serem observados.
Isso é feito tratando cada um como um problema de classificação binária usando a função sigmóide $\sigma(x) = \frac{1}{1 + e^{-x} }$.
Passo 2.1: Processar o Par Positivo (preto -> gato)
-
Calcular o Score:
\[s_{pos} = v^{'}\_{\text{gato} } \cdot v_{\text{preto} }\] \[s_{pos} = [0.1, 0.2, -0.2, 0.4] \cdot [0.4, -0.3, 0.1, 0.5]\] \[s_{pos} = (0.1)(0.4) + (0.2)(-0.3) + (-0.2)(0.1) + (0.4)(0.5)\] \[s_{pos} = 0.04 - 0.06 - 0.02 + 0.20 = 0.16\] -
Calcular a Probabilidade (Sigmoide): O alvo aqui é $1$ (par positivo).
\[P(\text{gato} \vert \text{preto})_{pos} = \sigma(s_{pos}) = \sigma(0.16) = \frac{1}{1 + e^{-0.16} } \approx \frac{1}{1 + 0.852} \approx 0.540\] -
Calcular o Gradiente para este Par: O gradiente em relação ao score é $(\sigma(s_{pos}) - \text{target}) = (0.540 - 1) = -0.460$. Este valor será usado para atualizar $v^{‘}_{\text{gato} }$ e $v_{\text{preto} }$.
-
Gradiente para $v^{‘}_{\text{gato} }$: $g \cdot v_{\text{preto} } = -0.460 \times [0.4, -0.3, 0.1, 0.5]$
-
Gradiente (contribuição) para $v_{\text{preto} }$: $g \cdot v^{‘}_{\text{gato} } = -0.460 \times [0.1, 0.2, -0.2, 0.4]$
-
Passo 2.2: Processar o Primeiro Par Negativo (preto -> cachorro).
- Amostrar Negativo: Escolhemos
cachorroaleatoriamente (evitandogato).
com um valor exemplo para $\eta$ (ex.: $\eta = 0.01$).
-
Calcular o Score:
\[s_{neg1} = v^{'}\_{\text{cachorro} } \cdot v_{\text{preto} }\] \[s_{neg1} = [0.1, -0.3, 0.8, -0.1] \cdot [0.4, -0.3, 0.1, 0.5]\] \[s_{neg1} = (0.1)(0.4) + (-0.3)(-0.3) + (0.8)(0.1) + (-0.1)(0.5)\] \[s_{neg1} = 0.04 + 0.09 + 0.08 - 0.05 = 0.16\] -
Calcular a Probabilidade (Sigmoide): O alvo aqui é $0$ (par negativo).
\[P(\text{cachorro} \vert \text{preto})_{neg} = \sigma(s_{neg1}) = \sigma(0.16) \approx 0.540\] -
Calcular o Gradiente para este Par: O gradiente em relação ao score é $(\sigma(s_{neg1}) - \text{target}) = (0.540 - 0) = 0.540$.
- Gradiente para $v^{‘}_{\text{cachorro} }$: $g \cdot v_{\text{preto} } = 0.540 \times [0.4, -0.3, 0.1, 0.5]$;
- Gradiente (contribuição) para $v_{\text{preto} }$: $g \cdot v^{‘}_{\text{cachorro} } = 0.540 \times [0.1, -0.3, 0.8, -0.1]$.
Passo 2.3: Processar o Segundo Par Negativo (preto -> jardim).
-
Amostrar Negativo: Escolhemos
jardimaleatoriamente (evitandogato). -
Calcular o Score:
\[s_{neg2} = v^{'}\_{\text{jardim} } \cdot v_{\text{preto} }\] \[s_{neg2} = [0.5, 0.1, 0.3, -0.2] \cdot [0.4, -0.3, 0.1, 0.5]\] \[s_{neg2} = (0.5)(0.4) + (0.1)(-0.3) + (0.3)(0.1) + (-0.2)(0.5)\] \[s_{neg2} = 0.20 - 0.03 + 0.03 - 0.10 = 0.10\] -
Calcular a Probabilidade (Sigmoide): O alvo aqui é $0$.
\[P(\text{jardim} \vert \text{preto})_{neg} = \sigma(s_{neg2}) = \sigma(0.10) = \frac{1}{1 + e^{-0.10} } \approx \frac{1}{1 + 0.905} \approx 0.525\] -
Calcular o Gradiente para este Par: O gradiente em relação ao score é $(\sigma(s_{neg2}) - \text{target}) = (0.525 - 0) = 0.525$.
- Gradiente para $v^{‘}_{\text{jardim} }$: $g \cdot v_{\text{preto} } = 0.525 \times [0.4, -0.3, 0.1, 0.5]$;
- Gradiente (contribuição) para $v_{\text{preto} }$: $g \cdot v^{‘}_{\text{jardim} } = 0.525 \times [0.5, 0.1, 0.3, -0.2]$;
Passo 3: atualização dos Vetores (usando Gradiente Descendente com taxa $\eta$):
-
Atualizar $v^{‘}_{\text{gato} }$ (Positivo):
\[v^{'}\_{\text{gato} } \leftarrow v^{'}\_{\text{gato} } - \eta \cdot (\sigma(s_{pos}) - 1) \cdot v_{\text{preto} }\] \[v^{'}\_{\text{gato} } \leftarrow v^{'}\_{\text{gato} } - \eta \cdot (-0.460) \cdot v_{\text{preto} }\] -
Atualizar $v^{‘}_{\text{cachorro} }$ (Negativo 1):
\[v^{'}\_{\text{cachorro} } \leftarrow v^{'}\_{\text{cachorro} } - \eta \cdot (\sigma(s_{neg1}) - 0) \cdot v_{\text{preto} }\] \[v^{'}\_{\text{cachorro} } \leftarrow v^{'}\_{\text{cachorro} } - \eta \cdot (0.540) \cdot v_{\text{preto} }\] -
Atualizar $v^{‘}_{\text{jardim} }$ (Negativo 2):
\[v^{'}\_{\text{jardim} } \leftarrow v^{'}\_{\text{jardim} } - \eta \cdot (\sigma(s_{neg2}) - 0) \cdot v_{\text{preto} }\] \[v^{'}\_{\text{jardim} } \leftarrow v^{'}\_{\text{jardim} } - \eta \cdot (0.525) \cdot v_{\text{preto} }\] -
Atualizar $v_{\text{preto} }$ (Entrada): O gradiente para $v_{\text{preto} }$ acumula as contribuições do par positivo e de todos os pares negativos.
\[\nabla_{v_{\text{preto} } } L = (\sigma(s_{pos}) - 1) v^{'}\_{\text{gato} } + (\sigma(s_{neg1}) - 0) v^{'}\_{\text{cachorro} } + (\sigma(s_{neg2}) - 0) v^{'}\_{\text{jardim} }\] \[v_{\text{preto} } \leftarrow v_{\text{preto} } - \eta \cdot \nabla_{v_{\text{preto} } } L\]
Passo 4: agora, a atenta leitora deve notar que só precisamos calcular scores e gradientes para a palavra positiva (gato) e as $k=2$ negativas (cachorro, jardim), um total de $k+1 = 3$ pares. Isso é muito mais rápido que calcular para todas as $\vert V \vert = 7$ palavras, como exigiria o Softmax completo. A complexidade é $O(k)$ em vez de $O(\vert V \vert)$. Além disso, apenas os vetores de saída ($v^{‘}$) das palavras envolvidas, tanto positivas quanto negativas, são atualizados neste passo. Os vetores de saída das outras palavras do vocabulário não são tocados. Finalmente, o vetor de entrada da palavra alvo, $v_{\text{preto} }$, é atualizado com base no erro combinado de todos os $k+1$ pares processados.
Este exemplo simplificado demonstra como o Negative Sampling reduz drasticamente a carga computacional ao focar em distinguir a palavra de contexto correta de apenas algumas amostras incorretas, tornando o treinamento de word embeddings viável em grandes conjuntos de dados.
Hierarchical Softmax
Utiliza uma árvore binária de Huffman para representar o vocabulário, reduzindo a complexidade para $O(\log \vert V \vert )$.
Uma Árvore Binária de Huffman é uma estrutura de dados em árvore utilizada principalmente para compressão de dados sem perdas. Ela é construída usando um algoritmo guloso, em inglês greedy, inventado por David A. Huffman.
O algoritmo de Huffman constrói uma árvore com base nas frequências dos símbolos, como caracteres ou palavras, que se deseja codificar. A ideia central é atribuir códigos binários de comprimento variável a cada símbolo:
- Símbolos mais frequentes recebem códigos binários mais curtos;
- Símbolos menos frequentes recebem códigos binários mais longos.
Para este algoritmo, a construção da árvore é feita da seguinte forma:
- cada símbolo começa como uma folha de árvore com sua frequência associada;
- iterativamente, os dois nós, folhas ou subárvores, com as menores frequências são selecionados e combinados para formar um novo nó interno. A frequência deste novo nó é a soma das frequências dos seus filhos;
- esse processo continua até que todos os nós sejam combinados em uma única árvore raiz.
Propriedades interessantes:
- Ótima: gera o código de prefixo com o menor comprimento médio esperado para um dado conjunto de frequências.
- Código de Prefixo: nenhum código atribuído a um símbolo é prefixo de outro código. Isso garante que a decodificação seja única e sem ambiguidades. Por exemplo, se
0é o código paraA, nenhum outro código pode começar com0(como01para `B).- Estrutura: é uma árvore binária completa, cada nó interno tem exatamente dois filhos. As folhas representam os símbolos originais, e o caminho da raiz até uma folha define o código binário para aquele símbolo. Por exemplo, seguir para a esquerda pode ser
0e para a direita1.Aplicação em Hierarchical Softmax: No contexto do Word2Vec, uma árvore de Huffman é construída para o vocabulário, usando as frequências das palavras. Palavras mais frequentes ficam mais perto da raiz. Implicando em caminhos/códigos mais curtos. A probabilidade de uma palavra é calculada navegando pela árvore, tornando o cálculo muito mais eficiente do que o Softmax padrão sobre todo o vocabulário.
A intuitiva leitora pode imaginar que o Hierarchical Softmax organiza o vocabulário em uma árvore binária de Huffman, onde palavras frequentes ficam mais perto da raiz. Para prever uma palavra, a rede só precisa aprender a fazer uma sequência de decisões binárias, próximo nó à esquerda/direita, para navegar da raiz até a folha correspondente à palavra correta. O número de decisões é logarítmico no tamanho do vocabulário ($O(\log \vert V \vert )$), tornando o processo muito mais rápido que o Softmax padrão ($O( \vert V \vert )$).
Exemplo Numérico de Hierarchical Softmax
Vamos ilustrar como o Hierarchical Softmax calcula a probabilidade $p(w_O \vert w_I)$.
Passo 1: Cenário Inicial:
- Vocabulário e Frequências (Simplificado):
gato: 50;cachorro: 45;corre: 30;late: 25;preto: 15.
-
Árvore de Huffman Construída (Exemplo): suponha que a construção resultou na árvore apresentada na Figura 9. Nesta árvore os vértices são $n_0$ a $n_3$, e as folhas são as palavras. Na Figura 10 eu adotei a convenção $0=\text{Esquerda}$, $1=\text{Direita}$.

Figura 9: Mostra uma árvore de Huffman com cinco palavras e suas respectivas propriedades.
- Códigos de Huffman Resultantes:
gato: 00cachorro: 01late: 100preto: 101corre: 11
-
Dimensão do Embedding: $d=3$.
-
Palavra de Entrada (Skip-Gram): $w_I = $
\[v_{\text{preto} } = [0.4, 0.1, -0.2]\]preto, com vetor (hipotético): -
Palavra de Saída (Contexto a prever): $w_O = $
corre. -
Vetores dos Nós Internos (Aprendidos/Hipotéticos): Cada nó interno $n_j$ tem um vetor $v^{‘}_{n_j}$ de dimensão $d=3$.
- $v^{‘}_{n0} = [0.1, 0.5, -0.1]$;
- $v^{‘}_{n1} = [-0.2, 0.3, 0.4]$ (Não usado para prever
corre); - $v^{‘}_{n2} = [0.3, -0.1, 0.2]$;
- $v^{‘}_{n3} = [0.6, 0.2, -0.3]$ (Não usado para prever
corre).
2. Calculando $p(\text{corre} \vert \text{preto})$:
Para prever corre, precisamos navegar da raiz ($n_0$) até a folha corre. O caminho é $n_0 \rightarrow n_2 \rightarrow \text{corre}$, que corresponde ao código Huffman 11.
-
Passo 1: Decisão no nó $n_0$.
-
Para chegar a
corre, precisamos ir para a direita (código1) em $n_0$. -
A probabilidade de ir para a direita será dada por $p(\text{direita} \vert n_0) = \sigma(-v^{‘}_{n0} \cdot v_{\text{preto} })$.
-
Calculamos o score: $s_0 = v^{‘}_{n0} \cdot v_{\text{preto} } = [0.1, 0.5, -0.1] \cdot [0.4, 0.1, -0.2]$
\[s_0 = (0.1)(0.4) + (0.5)(0.1) + (-0.1)(-0.2) = 0.04 + 0.05 + 0.02 = 0.11\] -
Calculamos a probabilidade: $p(\text{direita} \vert n_0) = \sigma(-s_0) = \sigma(-0.11) = \frac{1}{1 + e^{0.11} } \approx \frac{1}{1 + 1.116} \approx 0.473$
-
-
-
Passo 2: Decisão no nó $n_2$.
-
Vindo de $n_0$, chegamos a $n_2$. Para chegar a
corre, precisamos ir para a direita novamente (código1). -
A probabilidade de ir para a direita é $p(\text{direita} \vert n_2) = \sigma(-v^{‘}_{n2} \cdot v_{\text{preto} })$.
-
Calculamos o score: $s_2 = v^{‘}_{n2} \cdot v_{\text{preto} } = [0.3, -0.1, 0.2] \cdot [0.4, 0.1, -0.2]$
\[s_2 = (0.3)(0.4) + (-0.1)(0.1) + (0.2)(-0.2) = 0.12 - 0.01 - 0.04 = 0.07\] -
Calculamos a probabilidade: $p(\text{direita} \vert n_2) = \sigma(-s_2) = \sigma(-0.07) = \frac{1}{1 + e^{0.07} } \approx \frac{1}{1 + 1.072} \approx 0.483$
-
-
-
Passo 3: Calcular a Probabilidade Final.
-
A probabilidade total de prever
\[p(\text{corre} \vert \text{preto}) = p(\text{direita} \vert n_0) \times p(\text{direita} \vert n_2)\] \[p(\text{corre} \vert \text{preto}) \approx 0.473 \times 0.483 \approx 0.228\]correé o produto das probabilidades das decisões tomadas ao longo do caminho:
-
3. Treinamento (Conceitual):
-
Cálculo do Erro: A perda seria calculada como $L = -\log p(\text{corre} \vert \text{preto}) \approx -\log(0.228) \approx 1.478$.
-
Backpropagation: O erro seria propagado de volta ao longo do caminho $n_0 \rightarrow n_2$. Os gradientes seriam calculados para:
-
O vetor de entrada $v_{\text{preto} }$.
-
Os vetores dos nós internos no caminho: $v^{‘}_{n0}$ e $v^{‘}_{n2}$.
-
-
Atualização: Apenas $v_{\text{preto} }$, $v^{‘}_{n0}$ e $v^{‘}_{n2}$ seriam atualizados usando gradiente descendente. Os vetores dos outros nós internos ($v^{‘}_{n1}$, $v^{‘}_{n3}$) e os vetores de saída associados a outras palavras não são tocados neste passo.
Neste exemplo, para calcular a probabilidade de corre, realizamos apenas $2$ cálculos de score e sigmoide, um para cada nó interno no caminho. Com o Softmax padrão, teríamos que calcular scores para todas as $5$ palavras do vocabulário. A complexidade aqui é $O(\text{profundidade da palavra}) \approx O(\log \vert V \vert)$, que é muito menor que $O(\vert V \vert)$ para vocabulários grandes.
A atenta leitora deve ter percebido que a diferença na eficiência computacional entre o Softmax padrão e suas otimizações (Hierarchical Softmax - HS, Negative Sampling - NS) é drástica para vocabulários grandes.
Vamos considerar um vocabulário realista com $\vert V \vert = 100.000$ palavras.
-
Softmax Padrão: a complexidade é $O(\vert V \vert)$. Para calcular a probabilidade de uma palavra de saída, precisamos calcular $e^{\text{score} }$ para todas as 100.000 palavras no vocabulário e então somá-las para obter o denominador. Isso envolve aproximadamente 100.000 operações de exponenciação e adição/divisão por exemplo de treinamento.
-
Hierarchical Softmax: a complexidade é $O(\log_2 \vert V \vert)$. A estrutura de árvore binária (geralmente Huffman) permite calcular a probabilidade navegando da raiz até a folha da palavra correta. O número de passos (decisões binárias) é a profundidade da árvore, que é aproximadamente $\log_2(100.000)$.
\[\log_2(100.000) \approx 16.6\]Portanto, o Hierarchical Softmax requer cerca de 17 cálculos, normalmente produtos escalares seguidos de sigmóides, por exemplo de treinamento. Uma redução imensa! Quase inacreditável!
-
Negative Sampling: a complexidade é $O(k+1)$, onde $k$ é o número de amostras negativas escolhidas. Um valor comum para $k$ em modelos como Word2Vec é entre 5 e 20 para conjuntos de dados pequenos, e $2$ a $5$ para grandes. Se usarmos $k=5$:
A complexidade é $O(5+1) = O(6)$.
Isso significa que, para cada palavra de entrada, treinamos a rede para distinguir a palavra-alvo correta, $1$ classificação binária, de $5$ palavras erradas, $5$ classificações binárias, totalizando apenas 6 cálculos de classificação binária por exemplo de treinamento.
Eu acredito que neste ponto a esperta leitora deve ter percebido por que essas otimizações são essenciais para tornar o treinamento de word embeddings viável em grandes corpora de texto. A diferença na eficiência computacional entre o Softmax padrão e suas otimizações é drástica para vocabulários grandes.
Comparação:
- Softmax: ~100.000 operações/exemplo;
- HS: ~17 operações/exemplo;
- NS (k=5): ~6 operações/exemplo.
De Representações Estáticas para Contextuais: As Limitações e o Próximo Passo
As redes neurais rasas dos modelos tradicionais de word embeddings, como Word2Vec e GloVe, produzem embeddings estáticos. Isso significa que cada palavra no vocabulário possui um único vetor de representação, independentemente do contexto em que aparece. Por exemplo, a palavra banco teria o mesmo vetor em sentei no banco da praça e fui ao banco sacar dinheiro.
Essa abordagem, é muito melhor que as vetorizações inocente e probabilística, porém, a estimada leitora deve ter em mente que existem limitações significativas:
-
Polissemia: falha em capturar os múltiplos significados que uma única palavra pode ter. Por exemplo, a palavra
bancoteria o mesmo vetor de embedding nas frasessentei no banco da praça, um assento, efui ao banco sacar dinheiro, uma instituição financeira, embora os significados sejam completamente distintos. O embedding estático não consegue diferenciar esses usos contextuais. -
Dependência de Contexto: não consegue ajustar a representação da palavra com base nas palavras vizinhas que modificam seu sentido ou função gramatical.
Essas limitações motivaram a pesquisa em direção a representações de palavras contextuais, na qual o vetor de uma palavra depende da sentença em que ela se encontra. Isso levou a avanços subsequentes que utilizam redes neurais mais profundas e mecanismos mais sofisticados:
-
ELMo (Embeddings from Language Models) (2018): utilizou redes neurais recorrentes, LSTMs bidirecionais, profundas para gerar embeddings que variam conforme o contexto. A representação de uma palavra é uma função de todos os estados internos da LSTM.
-
BERT (Bidirectional Encoder Representations from Transformers) (2018): baseado na arquitetura Transformer, revolucionou o campo ao usar o mecanismo de auto-atenção (self-attention) para ponderar a influência de todas as palavras na sentença ao gerar a representação de cada palavra. Isso permite capturar relações complexas de longo alcance e gerar embeddings profundamente contextuais.
-
GPT (Generative Pre-trained Transformer) e seus sucessores: também baseados na arquitetura Transformer, principalmente no lado do decodificador, focam na geração de texto e aprendem representações contextuais poderosas através de pré-treinamento em larga escala.
Os modelos de word embeddings tradicionais, com sua arquitetura neural rasa, representaram um passo fundamental nessa evolução. Eles demonstraram o poder das representações distribuídas e estabeleceram a fundação sobre a qual modelos contextuais mais poderosos, como os Transformers, foram construídos, incorporando mecanismos adicionais como a atenção para superar as limitações dos embeddings estáticos.
Aspectos Práticos do Treinamento
Além dos conceitos teóricos, que a sagaz leitora analisou em todo este texto, alguns aspectos práticos são importantes ao treinar redes neurais, incluindo as usadas para word embeddings:
-
Inicialização de Pesos: a inicialização aleatória simples pode levar a problemas como gradientes explosivos ou desvanecentes. Métodos mais sofisticados como a Inicialização de Xavier/Glorot, para funções como sigmóide/tanh, ou Inicialização de He, para ReLU e suas variantes, ajudam a manter a variância dos sinais e gradientes estável através das camadas, facilitando o treinamento. Elas inicializam os pesos com base no número de neurônios de entrada e/ou saída da camada.
-
Ajuste de Hiperparâmetros: o desempenho da rede neural é altamente sensível aos hiperparâmetros, que são definidos antes do treinamento. Alguns dos mais importantes incluem:
-
Taxa de Aprendizado ($\eta$): controla o tamanho do passo na atualização dos pesos. Valores muito altos podem causar instabilidade; valores muito baixos podem tornar o treinamento lento ou preso em mínimos locais ruins. Técnicas de taxa de aprendizado adaptativa (como Adam, RMSprop) ou cronogramas de decaimento da taxa de aprendizado são comuns.
-
Tamanho do Mini-lote (Mini-batch Size): o número de exemplos usados para calcular o gradiente em cada atualização. Afeta a velocidade de treinamento e a estabilidade do gradiente.
-
Número de Épocas: quantas vezes o conjunto de treinamento completo é visto pela rede.
-
Arquitetura da Rede: número de camadas ocultas e número de neurônios por camada, para MLPs, ou a dimensão do embedding.
-
Parâmetros de Regularização: como a força da regularização L2 ($\lambda$) ou a taxa de dropout.
A escolha ótima desses hiperparâmetros geralmente requer experimentação e validação cruzada.
-
Validação Cruzada (Cross-Validation)
A validação cruzada é uma técnica de avaliação de modelos de aprendizado de máquina que visa estimar o desempenho do modelo em dados não vistos. Em vez de usar uma única divisão entre conjunto de treino e teste, a validação cruzada divide os dados em múltiplos subconjuntos e realiza várias iterações de treinamento e teste. Algumas técnicas comuns incluem:
K-Fold Cross-Validation: Os dados são divididos em k subconjuntos (folds). Em cada iteração, um subconjunto diferente é usado como teste, enquanto os k-1 restantes são usados para treino. O processo é repetido k vezes, e a performance final é a média dos resultados.
Leave-One-Out Cross-Validation (LOOCV): Caso especial do k-fold onde k é igual ao número de exemplos. A cada iteração, apenas um exemplo é usado para teste.
Stratified K-Fold: Variação do k-fold que mantém a proporção das classes em cada fold, importante para dados desbalanceados.
Benefícios:
- Fornece estimativa mais robusta da performance do modelo;
- Reduz o viés de seleção da divisão treino/teste;
- Ajuda a detectar overfitting;
- Permite usar todo o dataset para treinamento e validação.
-
Bibliotecas e Frameworks: implementar redes neurais do zero é instrutivo e serve para que a dedicada leitora entende todo o processo. Entretanto, na prática, o uso de bibliotecas e frameworks acelera significativamente o desenvolvimento e o treinamento.
-
No ecossistema Python, TensorFlow, Keras, frequentemente usada como interface de alto nível para TensorFlow, e PyTorch são extremamente populares, oferecendo blocos de construção otimizados, diferenciação automática, autograd, para calcular gradientes $\frac{\partial L}{\partial w}$ sem derivação manual, e suporte robusto a GPUs.
-
Para quem trabalha com C++, existem opções poderosas como a API C++ do TensorFlow, embora mais comumente usada para implantação/inferência de modelos treinados em Python, e a LibTorch, o frontend C++ do PyTorch, que trazem funcionalidades semelhantes, como tensores e diferenciação automática, diretamente para o C++. Finalmente temos o Caffe (Convolutional Architecture for Fast Feature Embedding). Um framework de aprendizado profundo desenvolvido na UC Berkeley, escrito primariamente em C++ com interfaces para Python e MATLAB. Foi criado com foco em três princípios fundamentais: expressividade, velocidade e modularidade. Além disso, bibliotecas nativas de C++ como mlpack, com foco em desempenho e facilidade de uso, e DyNet, especialmente forte para Processamento de Linguagem Natural e redes dinâmicas, fornecem implementações eficientes e são projetadas com C++ em mente, sendo valiosas em cenários onde o desempenho computacional ou a integração com sistemas C++ legados são críticos.
Referências
AGGARWAL, C. C. Neural networks and deep learning: a textbook. Cham: Springer, 2018.
BENGIO, Y. et al. A Neural Probabilistic Language Model. Journal of Machine Learning Research, v. 3, p. 1137-1155, 2003.
BERKELEY VISION AND LEARNING CENTER. Caffe: Convolutional Architecture for Fast Feature Embedding. Disponível em: https://caffe.berkeleyvision.org/. Acesso em: 26 abr. 2025.
BRAGA, A. P.; CARVALHO, A. P. L. F.; LUDERMIR, T. B. Redes neurais artificiais: teoria e aplicações. 2. ed. Rio de Janeiro: LTC, 2007.
CURTIN, R. R. et al. mlpack: A Scalable C++ Machine Learning Library. Journal of Machine Learning Research, v. 14, n. 1, p. 801-805, 2013. Disponível em: https://www.mlpack.org/. Acesso em: 26 abr. 2025.
GLOROT, X.; BENGIO, Y. Understanding the difficulty of training deep feedforward neural networks. Journal of Machine Learning Research - Proceedings Track, v. 9, p. 249-256, jan. 2010.
GLOROT, X.; BORDES, A.; BENGIO, Y. Deep sparse rectifier neural networks. In: Proceedings of the fourteenth international conference on artificial intelligence and statistics, p. 315-323, 2011.
GOODFELLOW, I.; BENGIO, Y.; COURVILLE, A. Deep Learning. Cambridge, MA: MIT Press, 2016.
HAYKIN, S. Redes neurais: princípios e prática. 2. ed. Porto Alegre: Bookman, 2001.
HAYKIN, S. Neural Networks and Learning Machines. 3rd ed. Upper Saddle River: Pearson, 2009.
HE, K.; ZHANG, X.; REN, S.; SUN, J. Deep Residual Learning for Image Recognition. In: IEEE CONFERENCE ON COMPUTER VISION AND PATTERN RECOGNITION (CVPR), 2016, Las Vegas. Proceedings […]. IEEE, 2016, p. 770-778. DOI: 10.1109/CVPR.2016.90.
HINTON, G. E.; SRIVASTAVA, N.; KRIZHEVSKY, A.; SUTSKEVER, I.; SALAKHUTDINOV, R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv preprint arXiv:1207.0580, 2012.
HUFFMAN, D. A. A Method for the Construction of Minimum-Redundancy Codes. Proceedings of the IRE, v. 40, n. 9, p. 1098-1101, 1952. DOI: 10.1109/JRPROC.1952.273898.
KERAS Team. Keras: Deep Learning para humanos. Disponível em: https://keras.io/. Acesso em: 26 abr. 2025.
MCCULLOCH, W. S.; PITTS, W. A logical calculus of the ideas immanent in nervous activity. The bulletin of mathematical biophysics, v. 5, n. 4, p. 115-133, 1943.
MIKOLOV, T.; CHEN, K.; CORRADO, G.; DEAN, J. Efficient Estimation of Word Representations in Vector Space. In: INTERNATIONAL CONFERENCE ON LEARNING REPRESENTATIONS (ICLR), 2013, Scottsdale. Proceedings. Scottsdale: ICLR, 2013. Disponível em: https://arxiv.org/abs/1301.3781. Acesso em: 26 abr. 2025.
MIKOLOV, T.; SUTSKEVER, I.; CHEN, K.; CORRADO, G.; DEAN, J. Distributed Representations of Words and Phrases and their Compositionality. In: ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS (NIPS), 26., 2013, Lake Tahoe. Proceedings […]. Lake Tahoe: NIPS, 2013. p. 3111-3119. Disponível em: https://proceedings.neurips.cc/paper/2013/hash/9aa42b31882ec039965f3c4923ce901b-Abstract.html. Acesso em: 26 abr. 2025.
MINSKY, M.; PAPERT, S. Perceptrons: An introduction to computational geometry. Cambridge, MA: MIT Press, 1969.
NAIR, V.; HINTON, G. E. Rectified linear units improve restricted boltzmann machines. In: Proceedings of the 27th international conference on machine learning (ICML-10), p. 807-814, 2010.
NIELSEN, M. Neural Networks and Deep Learning. Determination Press, 2015.
NEUBIG, G. et al. DyNet: The Dynamic Neural Network Toolkit. arXiv preprint arXiv:1701.03980, 2017. Disponível em: https://dynet.readthedocs.io/. Acesso em: 26 abr. 2025.
PYTORCH Team. PyTorch: Tensores e redes neurais dinâmicas em Python com forte aceleração por GPU. Disponível em: https://pytorch.org/. Acesso em: 26 abr. 2025.
PYTORCH Team. LibTorch: A interface C++ do PyTorch. Disponível em: https://pytorch.org/. Acesso em: 26 abr. 2025.
ROSENBLATT, F. The Perceptron: a probabilistic model for information storage and organization in the brain. Psychological review, v. 65, n. 6, p. 386-408, 1958.
RUMELHART, D. E.; HINTON, G. E.; WILLIAMS, R. J. Learning representations by back-propagating errors. Nature, v. 323, n. 6088, p. 533-536, 1986.
TENSORFLOW. TensorFlow: Uma plataforma de código aberto para aprendizado de máquina. Disponível em: https://www.tensorflow.org/. Acesso em: 26 abr. 2025.
TENSORFLOW. API C++ do TensorFlow. Disponível em: https://www.tensorflow.org/api_docs/cc. Acesso em: 26 abr. 2025.
VASWANI, A. et al. Attention is All You Need. Advances in Neural Information Processing Systems, v. 30, 2017.
