Transformers - A Temida Matemática
Neste artigo, a curiosa leitora irá enfrentar os Transformers. Nenhuma relação com o o Optimus Prime. Se for estes Transformers que está procurando, o Google falhou com você!
Neste texto vamos discutir os Transformers modelos de aprendizado de máquina que revolucionaram o processamento de linguagem natural (NLP). Estas técnicas foram apresentados ao mundo em um artigo intitulado Attention is All You Need (Atenção é Tudo que Você Precisa), publicado em 20171 na conferência Advances in Neural Information Processing Systems (NeurIPS). Observe, atenta leitora que isso se deu há quase 10 anos. No ritmo atual, uma eternidade.
O entendimento da linguagem natural por máquinas é, ou era, um desafio importante que beirava o impossível. Este problema parece estar resolvido. Se isso for verdade, terá sido graças as técnicas e algoritmos, criados em torno de aprendizado de máquinas e estatísticas. Ou se preferir, podemos dizer que Usamos algoritmos determinísticos para aplicar técnicas estocásticas em bases de dados gigantescas e assim, romper os limites que haviam sido impostos pela linguística matemática e computacional determinísticas.
Veremos como esses modelos, inicialmente projetados para tradução automática, se tornaram a base para tarefas como geração de texto, como no GPT-3, compreensão de linguagem e até mesmo processamento de áudio.
Começaremos com as técnicas de representação mais simples e os conceitos matemáticos fundamentais: produtos escalares e multiplicação de matrizes. E, gradualmente, construiremos nosso entendimento. O que suporta todo este esforço é a esperança que a esforçada leitora possa acompanhar o raciocínio e entender como os Transformers funcionam a partir do seu cerne.
Finalmente, os exemplos. O combinado será o seguinte: aqui eu faço em C++ 20. Depois, a leitora faz em Python, C, C++ ou qualquer linguagem que desejar. Se estiver de acordo continuamos.
Para que os computadores processem e compreendam a linguagem humana, é essencial converter texto em representações numéricas. Esse treco burro só entende binário. Dito isso, vamos ter que, de alguma forma, mapear o conjunto dos termos que formam uma linguagem natural no conjunto dos binários que o computador entende. Ou, em outras palavras, temos que representar textos em uma forma matemática que os computadores possam manipular. Essa representação é o que chamamos de vetorização.
Vetores, os compassos de tudo que há e haverá
Eu usei exatamente esta frase em um texto sobre eletromagnetismo. A ideia, então era explicar eletromagnetismo a partir da matemática. Lá há uma definição detalhada de vetores e todas as suas operações. Aqui, podemos ser um tanto mais diretos. Vetores são os artefatos matemáticos que usamos para explicar o universo.
Um vetor é uma entidade matemática que possui tanto magnitude, ou comprimento, quanto direção. Um vetor pode ser definido como um segmento de reta direcionado na geometria, ou uma sequência ordenada de números, chamados de componentes, na álgebra. A representação depende do contexto. Aqui, vamos nos concentrar na representação algébrica, que é mais comum em programação e computação.
Na geometria, um vetor pode ser visualizado como uma seta em um espaço, por exemplo, em um plano $2D$ ou em um espaço $3D$. O comprimento da seta representa a magnitude, e a direção da seta indica a direção do vetor. Imagine uma seta apontando para cima e para a direita em um plano. Essa seta é um vetor com uma certa magnitude (o comprimento da seta) e uma direção ($45$ graus em relação ao eixo horizontal, por exemplo). A Figura 1 mostra um vetor como usado na matemática e na física.
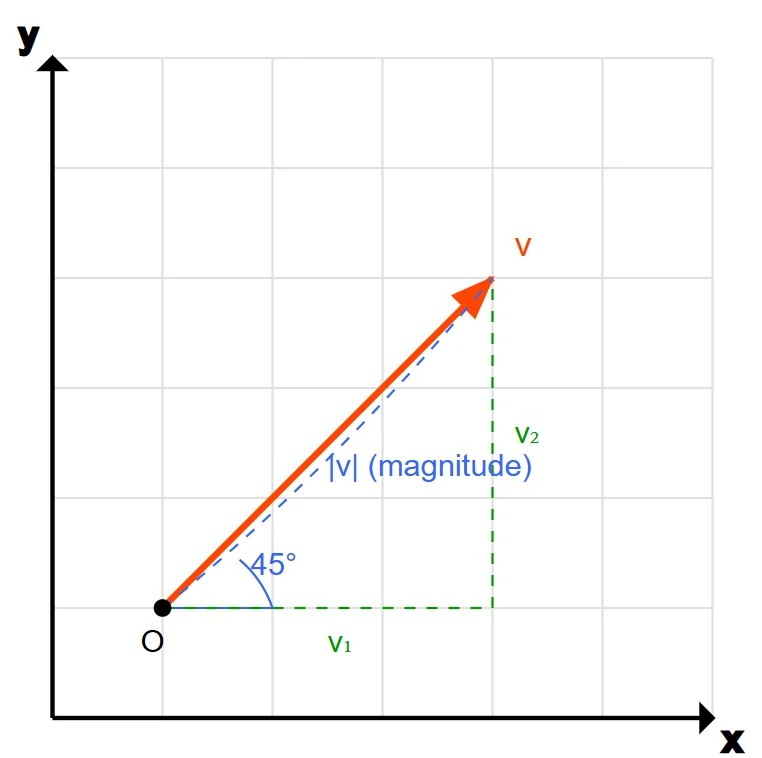Figura 1: Um vetor partindo da origem $O$ com comprimento $\mid V \mid$ e dimensões $V_1$ e $V_2$.
Em um sistema algébrico de coordenadas, um vetor pode ser representado como uma tupla. Por exemplo, em um espaço tridimensional, um vetor pode ser escrito como $(x, y, z)$, onde $x$, $y$ e $z$ são as componentes do vetor ao longo dos eixos $x$, $y$ e $z$, respectivamente. Assim, se nos limitarmos a $2D$, o vetor $(2, 3)$ representa um deslocamento de $2$ unidades na direção $x$ e $3$ unidades na direção $y$. Na Figura 1 podemos ver um vetor $V$ partindo da origem $O$ e terminando no ponto $P(V_1, V_2)$.
Espaço Vetorial
Para compreender vetores e suas operações, precisamos primeiro entender um conceito algébrico, o conceito de espaço vetorial.
Um espaço vetorial é uma estrutura matemática que formaliza a noção de operações geométricas como adição de vetores e multiplicação por escalares.
Formalmente, um espaço vetorial sobre um corpo $F$ é um conjunto $V$ no qual há adição de vetores e multiplicação por escalares em $F$, obedecendo axiomas que garantem associatividade, comutatividade, existência de neutro e inverso aditivo, além de compatibilidade entre multiplicação por escalar e estrutura do corpo.
Em processamento de linguagem natural, trabalharemos principalmente com o espaço vetorial real $\mathbb{R}^n$, onde $n$ representa a dimensão do espaço vetorial. Ou, em nosso caso, quantos itens teremos no nosso vetor. Logo, $\mathbb{R}^n$ representa o espaço vetorial que contém todas as $n$-tuplas ordenadas de números reais. Formalmente, definimos $\mathbb{R}^n$ como:
\[\mathbb{R}^n = \{(x_1, \ldots, x_n) : x_i \in \mathbb{R} \text{ para } i = 1, \ldots, n\}\]Quando representarmos palavras (termos), ou documentos, como vetores, estaremos mapeando elementos linguísticos para pontos em um espaço dado por $\mathbb{R}^n$. Neste caso, a dimensão $n$ será determinada pelo método específico de vetorização que escolhermos.
Ao converter textos e elementos linguísticos em representações vetoriais, criamos word embeddings. Técnicas que mapeiam palavras ou frases para vetores de números reais. Esta representação tenta capturar tanto o significado semântico quanto as relações contextuais entre palavras em um espaço vetorial contínuo. Um desenvolvimento importante nesse campo são os Mecanismos de Atenção, que utilizam vetores de consulta (query), chave (key) e valor (value) como componentes essenciais. Estes mecanismos constituem o núcleo da arquitetura dos Transformers, permitindo que o modelo pondere a importância relativa de diferentes elementos em uma sequência, melhorando significativamente a capacidade de processamento de dependências de longo alcance em textos. Para entender isso, precisamos entender como fazer operações algébricas com vetores.
Operações com Vetores
Dado que estejam em um espaço vetorial, os vetores podem ser somados, subtraídos, multiplicados entre si e por escalares. Neste caso, a curiosa leitora deve saber que escalares são entidades sem direção. As operações sobre vetores têm interpretações geométricas e algébricas. Focando apenas nas interpretações algébricas, temos:
-
Soma: somamos vetores componente a componente. Exemplo: se tivermos $\vec{a}= (1, 2)$ e $\vec{b}= (3, -1)$ então $\vec{a} + \vec {b}$ será dado por $(1, 2) + (3, -1) = (4, 1)$;
-
Oposto: Dado um vetor $\vec{v} = (v_1, v_2, \ldots, v_n)$ no espaço $\mathbb{R}^n$, seu oposto será dado por $-\vec{v} = (-v_1, -v_2, \ldots, -v_n)$. Ou seja, o vetor oposto é o vetor que aponta na direção oposta e tem a mesma magnitude. Exemplo: se $\vec{a}= (1, 2)$ o oposto de $\vec{a}$ será dado por $-\vec{a} = (-1, -2)$;
-
Multiplicação por escalar: multiplicar um vetor por um escalar altera a sua magnitude, mas não a sua direção, a menos que o escalar seja negativo, caso em que a direção é invertida. Exemplo: dado $\vec{a} = (1, 2)$ o dobro de $\vec{a}$ será dado por $2 * (1, 2) = (2, 4)$;
Exemplo Operações com Vetores em C++ 20
#include <iostream> ///< Para entrada e saída padrão (std::cout, std::cerr).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de componentes.
#include <numeric> ///< Para std::inner_product, usado no cálculo do produto escalar.
#include <cmath> ///< Para std::sqrt e std::abs, usados em cálculos de magnitude.
#include <concepts> ///< Para std::is_arithmetic_v, usado no conceito Arithmetic.
#include <stdexcept> ///< Para exceções padrão como std::out_of_range e std::invalid_argument.
#include <string> ///< Para std::string e std::to_string, usados na conversão para string.
#include <sstream> ///< Para std::stringstream, usado na formatação de números de ponto flutuante.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <initializer_list> ///< Para suporte a inicialização de vetores com listas inicializadoras.
#include <algorithm> ///< Para std::abs, usado em cálculos de magnitude.
/**
* @concept Arithmetic
* @brief Conceito para garantir que um tipo é aritmético (integral ou de ponto flutuante).
*
* Restringe os parâmetros de template a tipos aritméticos (por exemplo, int, double, float).
*/
template<typename T>
concept Arithmetic = std::is_arithmetic_v<T>;
/**
* @class MathVector
* @brief Uma classe genérica para representar e manipular vetores matemáticos.
*
* Fornece operações como adição, subtração, multiplicação por escalar, produto escalar,
* cálculo de magnitude e normalização. Suporta vetores de qualquer tipo aritmético.
*
* @tparam T O tipo aritmético dos componentes do vetor (por exemplo, int, double).
*/
template<Arithmetic T>
class MathVector {
private:
std::vector<T> components; ///< Armazenamento interno para os componentes do vetor.
static constexpr T epsilon = 1e-9; ///< Constante pequena para comparações de ponto flutuante.
public:
/**
* @brief Construtor padrão que cria um vetor vazio.
*/
MathVector() = default;
/**
* @brief Constrói um vetor a partir de uma lista inicializadora.
* @param init Lista inicializadora contendo os componentes do vetor.
*/
MathVector(std::initializer_list<T> init) : components(init) {}
/**
* @brief Constrói um vetor a partir de um std::vector.
* @param vec O vetor de entrada contendo os componentes.
*/
explicit MathVector(const std::vector<T>& vec) : components(vec) {}
/**
* @brief Constrói um vetor de tamanho especificado com todos os componentes inicializados com um valor.
* @param n O número de componentes.
* @param val O valor inicial para todos os componentes (padrão é T{}).
*/
explicit MathVector(size_t n, T val = T{}) : components(n, val) {}
/**
* @brief Retorna o número de dimensões (componentes) do vetor.
* @return O tamanho do vetor.
*/
size_t dimensions() const {
return components.size();
}
/**
* @brief Fornece acesso não constante a um componente do vetor.
* @param index O índice do componente a acessar.
* @return Referência ao componente no índice especificado.
* @throws std::out_of_range Se o índice estiver fora dos limites.
*/
T& operator[](size_t index) {
if (index >= dimensions()) {
throw std::out_of_range("Índice fora dos limites do vetor");
}
return components[index];
}
/**
* @brief Fornece acesso constante a um componente do vetor.
* @param index O índice do componente a acessar.
* @return Referência constante ao componente no índice especificado.
* @throws std::out_of_range Se o índice estiver fora dos limites.
*/
const T& operator[](size_t index) const {
if (index >= dimensions()) {
throw std::out_of_range("Índice fora dos limites do vetor");
}
return components[index];
}
/**
* @brief Soma dois vetores componente a componente.
* @param other O vetor a ser somado a este vetor.
* @return Um novo vetor representando a soma.
* @throws std::invalid_argument Se os vetores tiverem dimensões diferentes.
*/
MathVector<T> operator+(const MathVector<T>& other) const {
if (dimensions() != other.dimensions()) {
throw std::invalid_argument("Não é possível somar vetores de dimensões diferentes");
}
MathVector<T> result(dimensions());
for (size_t i = 0; i < dimensions(); ++i) {
result[i] = components[i] + other[i];
}
return result;
}
/**
* @brief Subtrai um vetor de outro componente a componente.
* @param other O vetor a ser subtraído deste vetor.
* @return Um novo vetor representando a diferença.
* @throws std::invalid_argument Se os vetores tiverem dimensões diferentes.
*/
MathVector<T> operator-(const MathVector<T>& other) const {
if (dimensions() != other.dimensions()) {
throw std::invalid_argument("Não é possível subtrair vetores de dimensões diferentes");
}
MathVector<T> result(dimensions());
for (size_t i = 0; i < dimensions(); ++i) {
result[i] = components[i] - other[i];
}
return result;
}
/**
* @brief Multiplica o vetor por um escalar.
* @param scalar O valor escalar para multiplicação.
* @return Um novo vetor com componentes escalados.
*/
MathVector<T> operator*(T scalar) const {
MathVector<T> result(dimensions());
for (size_t i = 0; i < dimensions(); ++i) {
result[i] = components[i] * scalar;
}
return result;
}
/**
* @brief Retorna o vetor oposto (negado).
* @return Um novo vetor com todos os componentes negados.
*/
MathVector<T> operator-() const {
MathVector<T> result(dimensions());
for (size_t i = 0; i < dimensions(); ++i) {
result[i] = -components[i];
}
return result;
}
/**
* @brief Calcula o produto escalar deste vetor com outro.
* @param other O outro vetor para o produto escalar.
* @return O resultado escalar do produto escalar.
* @throws std::invalid_argument Se os vetores tiverem dimensões diferentes.
*/
T dot(const MathVector<T>& other) const {
if (dimensions() != other.dimensions()) {
throw std::invalid_argument("Não é possível calcular o produto escalar de vetores de dimensões diferentes");
}
return std::inner_product(components.begin(), components.end(), other.components.begin(), T(0));
}
/**
* @brief Calcula a magnitude euclidiana (norma L2) do vetor.
* @return A magnitude do vetor.
* @note Para tipos integrais, converte para double para sqrt e converte de volta.
*/
T magnitude() const {
T sum_of_squares = this->dot(*this);
if constexpr (std::is_integral_v<T>) {
return static_cast<T>(std::sqrt(static_cast<double>(sum_of_squares)));
} else {
return std::sqrt(sum_of_squares);
}
}
/**
* @brief Normaliza o vetor para ter comprimento unitário.
* @return Um novo vetor normalizado.
* @throws std::domain_error Se a magnitude do vetor for zero ou próxima de zero.
*/
MathVector<T> normalize() const {
T mag = magnitude();
if (std::abs(mag) < epsilon) {
throw std::domain_error("Não é possível normalizar um vetor de magnitude zero (ou muito próxima de zero)");
}
MathVector<T> result(dimensions());
for (size_t i = 0; i < dimensions(); ++i) {
result[i] = components[i] / mag;
}
return result;
}
/**
* @brief Converte o vetor para uma representação em string.
* @return Uma string representando o vetor (por exemplo, "[1.0000, 2.0000]").
* @note Para tipos de ponto flutuante, usa precisão fixa de 4 casas decimais.
*/
std::string to_string() const {
std::string result = "[";
for (size_t i = 0; i < dimensions(); ++i) {
if constexpr (std::is_floating_point_v<T>) {
std::stringstream ss;
ss << std::fixed << std::setprecision(4) << components[i];
result += ss.str();
} else {
result += std::to_string(components[i]);
}
if (i < dimensions() - 1) {
result += ", ";
}
}
result += "]";
return result;
}
/**
* @brief Fornece iterador para o início dos componentes do vetor.
* @return Iterador para o primeiro componente.
*/
auto begin() const {
return components.begin();
}
/**
* @brief Fornece iterador para o fim dos componentes do vetor.
* @return Iterador após o último componente.
*/
auto end() const {
return components.end();
}
/**
* @brief Fornece iterador não constante para o início dos componentes do vetor.
* @return Iterador para o primeiro componente.
*/
auto begin() {
return components.begin();
}
/**
* @brief Fornece iterador não constante para o fim dos componentes do vetor.
* @return Iterador após o último componente.
*/
auto end() {
return components.end();
}
/**
* @brief Retorna o vetor de componentes subjacente.
* @return Referência constante ao std::vector interno de componentes.
*/
const std::vector<T>& get_components() const {
return components;
}
};
/**
* @brief Multiplica um escalar por um vetor (escalar * vetor).
* @tparam T O tipo aritmético dos componentes do vetor.
* @param scalar O valor escalar.
* @param vec O vetor a ser multiplicado.
* @return Um novo vetor com componentes escalados.
*/
template<Arithmetic T>
MathVector<T> operator*(T scalar, const MathVector<T>& vec) {
return vec * scalar;
}
/**
* @brief Imprime um MathVector com um nome especificado.
* @tparam T O tipo aritmético dos componentes do vetor.
* @param vec O vetor a ser impresso.
* @param name O nome a ser exibido ao lado do vetor.
*/
template<Arithmetic T>
void print_mathvector(const MathVector<T>& vec, const std::string& name) {
std::cout << name << " = " << vec.to_string() << "\n";
}
/**
* @brief Função principal que demonstra operações com a classe MathVector.
*
* Este programa ilustra o uso da classe MathVector para realizar operações como adição,
* subtração, multiplicação por escalar, cálculo do vetor oposto, produto escalar,
* magnitude e normalização de vetores, com tratamento de erros robusto.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
std::cout << std::fixed << std::setprecision(4);
std::cout << "Demonstração de Operações com MathVector\n";
std::cout << "---------------------------------------\n\n";
// Inicialização dos vetores
MathVector<double> a = {2.0, 5.0, 1.0}; ///< Primeiro vetor para demonstração.
MathVector<double> b = {3.0, 1.0, 4.0}; ///< Segundo vetor para demonstração.
// Exemplo 1: Operações básicas
std::cout << "Exemplo 1: Operações básicas\n";
try {
print_mathvector(a, "Vetor a");
print_mathvector(b, "Vetor b");
// Adição
MathVector<double> sum = a + b;
print_mathvector(sum, "a + b");
// Subtração
MathVector<double> diff = a - b;
print_mathvector(diff, "a - b");
// Multiplicação por escalar
MathVector<double> scaled = 2.0 * a;
print_mathvector(scaled, "2 * a");
// Vetor oposto
MathVector<double> opposite = -a;
print_mathvector(opposite, "-a");
} catch (const std::exception& e) {
std::cerr << "Erro nas operações básicas: " << e.what() << "\n";
}
// Exemplo 2: Produto escalar
std::cout << "\nExemplo 2: Produto escalar\n";
try {
double dot_product = a.dot(b);
std::cout << "a · b = " << dot_product << "\n";
} catch (const std::exception& e) {
std::cerr << "Erro no cálculo do produto escalar: " << e.what() << "\n";
}
// Exemplo 3: Magnitude e normalização
std::cout << "\nExemplo 3: Magnitude e normalização\n";
try {
double mag_a = a.magnitude();
std::cout << "Magnitude de a = " << mag_a << "\n";
MathVector<double> a_normalized = a.normalize();
print_mathvector(a_normalized, "Vetor a normalizado");
std::cout << "Magnitude de a normalizado = " << a_normalized.magnitude() << "\n";
} catch (const std::exception& e) {
std::cerr << "Erro no cálculo de magnitude ou normalização: " << e.what() << "\n";
}
return 0;
}
Produto Escalar
Entre as operações entre vetores vamos começar com os produtos escalares, também conhecidos como produto interno. Neste caso, temos uma técnica para multiplicar vetores de forma que o resultado seja um escalar, um número sem dimensão. Para obter o produto escalar, representado por $\cdot$, de dois vetores, multiplicamos seus elementos correspondentes e, em seguida, somamos os resultados das multiplicações. Matematicamente temos:
\[\text{Se } \vec{a} = [a_1, a_2, ..., a_n] \text{ e } \vec{b} = [b_1, b_2, ..., b_n], \text{ então:}\] \[\vec{a} \cdot \vec{b} = \sum_{i=1}^{n} a_i b_i = a_1b_1 + a_2b_2 + ... + a_nb_n\]A Figura 2 mostra um diagrama desta operação com os dois vetores que usamos acima para facilitar o entendimento.
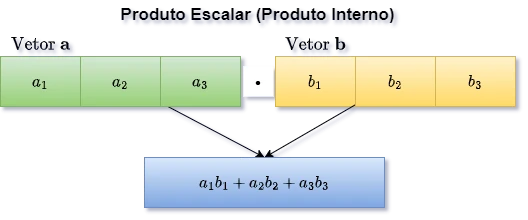
Figura 2: Entendendo o produto escalar entre dois vetores.
Exemplo 1: Considerando os vetores $\vec{a} = [2, 5, 1]$ e $\vec{b} = [3, 1, 4]$. O produto escalar será dado por:
\[\vec{a} \cdot \vec{b} = (2 * 3) + (5 * 1) + (1 * 4) = 6 + 5 + 4 = 15\]O produto escalar também pode ser representado na forma matricial. Se considerarmos os vetores como matrizes, o produto escalar será obtido multiplicando a transposta do primeiro vetor pelo segundo vetor:
\[\vec{a} \cdot \vec{b} = \vec{a}^T\vec{b} = \begin{bmatrix} a_1 & a_2 & \cdots & a_n \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} = \sum_{i=1}^{n} a_i b_i\]A transposta de um vetor é uma operação da álgebra linear que altera a orientação do vetor, convertendo um vetor coluna em um vetor linha ou vice-versa. Formalmente:
Se $\vec{v}$ é um vetor coluna $\vec{v} = \begin{pmatrix} v_1 \ v_2 \ \vdots \ v_n \end{pmatrix}$, sua transposta $\vec{v}^T$ é um vetor linha $\vec{v}^T = \begin{pmatrix} v_1 & v_2 & \cdots & v_n \end{pmatrix}$
Se $\vec{v}$ é um vetor linha $\vec{v} = \begin{pmatrix} v_1 & v_2 & \cdots & v_n \end{pmatrix}$, sua transposta $\vec{v}^T$ é um vetor coluna $\vec{v}^T = \begin{pmatrix} v_1 \ v_2 \ \vdots \ v_n \end{pmatrix}$
Em notação matricial, se representarmos um vetor coluna $\vec{v} \in \mathbb{R}^n$ como uma matriz $n \times 1$, sua transposta $\vec{v}^T$ será uma matriz $1 \times n$. A operação de transposição é indicada pelo sobrescrito $T$.
Em sistemas de processamento de linguagem natural, a transposição de vetores é frequentemente utilizada em operações de atenção e em cálculos de similaridade entre vetores de embedding.
Para ilustrar, considere os vetores $\vec{a} = [2, 5, 1]$ e $\vec{b} = [3, 1, 4]$. Na forma matricial, temos:
\[\vec{a}^T\vec{b} = \begin{bmatrix} 2 & 5 & 1 \end{bmatrix} \begin{bmatrix} 3 \\ 1 \\ 4 \end{bmatrix} = (2 \times 3) + (5 \times 1) + (1 \times 4) = 15\]Produto Escalar com Bibliotecas Numéricas
Em Python podemos usar o JAX, uma biblioteca para computação de alta performance com suporte para diferenciação automática, o produto escalar pode ser calculado usando a função jax.numpy.dot() ou o operador @.
import jax.numpy as jnp
# Defina dois vetores
v1 = jnp.array([1, 2, 3])
v2 = jnp.array([4, 5, 6])
# Calcule o produto escalar usando dot()
dot_product1 = jnp.dot(v1, v2)
# Calcule o produto escalar usando o operador @
dot_product2 = v1 @ v2
print(f"Produto escalar usando dot(): {dot_product1}")
print(f"Produto escalar usando @: {dot_product2}")
Em C++ podemos usar o Eigen, uma biblioteca de álgebra linear de alto desempenho, o produto escalar pode ser calculado usando o método dot() ou o operador de multiplicação de matrizes.
#include <iostream>
#include <Eigen/Dense>
/**
* @brief Função principal que demonstra o cálculo do produto escalar usando a biblioteca Eigen.
*
* Este programa define dois vetores tridimensionais e calcula seu produto escalar de duas formas:
* utilizando o método `dot()` da biblioteca Eigen e utilizando a multiplicação matricial com a transposta
* de um dos vetores. Os resultados são exibidos no console.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
// Defina dois vetores tridimensionais
Eigen::Vector3d v1(1, 2, 3);
Eigen::Vector3d v2(4, 5, 6);
// Calcula o produto escalar usando o método dot()
double dot_product1 = v1.dot(v2);
// Calcula o produto escalar usando a transposta e multiplicação matricial
double dot_product2 = v1.transpose() * v2;
std::cout << "Produto escalar usando dot(): " << dot_product1 << std::endl;
std::cout << "Produto escalar usando transpose e multiplicação: " << dot_product2 << std::endl;
return 0;
}
}
Exemplo em C++ 20 de Produto Escalar
#include <iostream> ///< Para entrada e saída padrão (std::cout, std::cerr).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de componentes.
#include <numeric> ///< Para std::inner_product, usado no cálculo do produto escalar.
#include <cmath> ///< Para funções matemáticas como std::sqrt e std::abs.
#include <concepts> ///< Para std::is_arithmetic_v, usado no conceito Arithmetic.
#include <stdexcept> ///< Para exceções padrão como std::out_of_range e std::invalid_argument.
#include <string> ///< Para std::string e std::to_string, usados na conversão para string.
#include <sstream> ///< Para std::stringstream, usado na formatação de números de ponto flutuante.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <initializer_list> ///< Para suporte a inicialização de vetores com listas inicializadoras.
/**
* @concept Arithmetic
* @brief Conceito para garantir que um tipo é aritmético (integral ou de ponto flutuante).
*
* Restringe os parâmetros de template a tipos aritméticos (por exemplo, int, double, float).
*/
template<typename T>
concept Arithmetic = std::is_arithmetic_v<T>;
/**
* @class MathVector
* @brief Uma classe genérica para representar e manipular vetores matemáticos.
*
* Suporta operações como produto escalar, cálculo de magnitude e conversão para string.
* Esta é uma implementação simplificada, com funcionalidades completas conforme o Bloco 1 do documento original.
*
* @tparam T O tipo aritmético dos componentes do vetor (por exemplo, int, double).
*/
template<Arithmetic T>
class MathVector {
private:
std::vector<T> components; ///< Armazenamento interno para os componentes do vetor.
static constexpr T epsilon = 1e-9; ///< Constante pequena para comparações de ponto flutuante.
public:
/**
* @brief Construtor padrão que cria um vetor vazio.
*/
MathVector() = default;
/**
* @brief Constrói um vetor a partir de uma lista inicializadora.
* @param init Lista inicializadora contendo os componentes do vetor.
*/
MathVector(std::initializer_list<T> init) : components(init) {}
/**
* @brief Constrói um vetor a partir de um std::vector.
* @param vec O vetor de entrada contendo os componentes.
*/
explicit MathVector(const std::vector<T>& vec) : components(vec) {}
/**
* @brief Constrói um vetor de tamanho especificado com todos os componentes inicializados com um valor.
* @param n O número de componentes.
* @param val O valor inicial para todos os componentes (padrão é T{}).
*/
explicit MathVector(size_t n, T val = T{}) : components(n, val) {}
/**
* @brief Retorna o número de dimensões (componentes) do vetor.
* @return O tamanho do vetor.
*/
size_t dimensions() const { return components.size(); }
/**
* @brief Fornece acesso não constante a um componente do vetor.
* @param index O índice do componente a acessar.
* @return Referência ao componente no índice especificado.
* @throws std::out_of_range Se o índice estiver fora dos limites.
*/
T& operator[](size_t index) {
if (index >= dimensions()) throw std::out_of_range("Índice fora dos limites do vetor");
return components[index];
}
/**
* @brief Fornece acesso constante a um componente do vetor.
* @param index O índice do componente a acessar.
* @return Referência constante ao componente no índice especificado.
* @throws std::out_of_range Se o índice estiver fora dos limites.
*/
const T& operator[](size_t index) const {
if (index >= dimensions()) throw std::out_of_range("Índice fora dos limites do vetor");
return components[index];
}
/**
* @brief Calcula o produto escalar deste vetor com outro.
* @param other O outro vetor para o produto escalar.
* @return O resultado escalar do produto escalar.
* @throws std::invalid_argument Se os vetores tiverem dimensões diferentes.
*/
T dot(const MathVector<T>& other) const {
if (dimensions() != other.dimensions()) throw std::invalid_argument("Dimensões diferentes para produto escalar");
return std::inner_product(components.begin(), components.end(), other.components.begin(), T(0));
}
/**
* @brief Calcula a magnitude euclidiana (norma L2) do vetor.
* @return A magnitude do vetor.
* @note Para tipos integrais, converte para double para sqrt e converte de volta.
*/
T magnitude() const {
T sum_of_squares = this->dot(*this);
if constexpr (std::is_integral_v<T>) return static_cast<T>(std::sqrt(static_cast<double>(sum_of_squares)));
else return std::sqrt(sum_of_squares);
}
/**
* @brief Converte o vetor para uma representação em string.
* @return Uma string representando o vetor (por exemplo, "[1.0000, 2.0000]").
* @note Para tipos de ponto flutuante, usa precisão fixa de 4 casas decimais.
*/
std::string to_string() const {
std::string result = "[";
for (size_t i = 0; i < dimensions(); ++i) {
if constexpr (std::is_floating_point_v<T>) {
std::stringstream ss;
ss << std::fixed << std::setprecision(4) << components[i];
result += ss.str();
} else {
result += std::to_string(components[i]);
}
if (i < dimensions() - 1) result += ", ";
}
result += "]"; return result;
}
/**
* @brief Retorna o vetor de componentes subjacente.
* @return Referência constante ao std::vector interno de componentes.
*/
const std::vector<T>& get_components() const { return components; }
};
/**
* @brief Imprime um MathVector com um nome especificado.
* @tparam T O tipo aritmético dos componentes do vetor.
* @param vec O vetor a ser impresso.
* @param name O nome a ser exibido ao lado do vetor.
*/
template<Arithmetic T>
void print_mathvector(const MathVector<T>& vec, const std::string& name) {
std::cout << name << " = " << vec.to_string() << "\n";
}
/**
* @class Matrix
* @brief Uma classe genérica para representar e manipular matrizes.
*
* Suporta operações como multiplicação de matrizes, transposição e conversão de vetores para matrizes linha/coluna.
*
* @tparam T O tipo aritmético dos elementos da matriz.
*/
template<Arithmetic T>
class Matrix {
private:
std::vector<std::vector<T>> data; ///< Armazenamento interno para os elementos da matriz.
size_t rows; ///< Número de linhas.
size_t cols; ///< Número de colunas.
public:
/**
* @brief Constrói uma matriz com dimensões especificadas e valor inicial.
* @param n Número de linhas.
* @param m Número de colunas.
* @param initial_value Valor inicial para todos os elementos (padrão é T{}).
*/
Matrix(size_t n, size_t m, T initial_value = T{})
: rows(n), cols(m), data(n, std::vector<T>(m, initial_value)) {}
/**
* @brief Constrói uma matriz a partir de um vetor de vetores.
* @param values Os dados de entrada como um vetor de vetores.
* @throws std::invalid_argument Se as linhas tiverem tamanhos inconsistentes.
*/
Matrix(const std::vector<std::vector<T>>& values) {
if (values.empty()) {
rows = 0;
cols = 0;
} else {
rows = values.size();
cols = values[0].size();
for (const auto& row : values) {
if (row.size() != cols) throw std::invalid_argument("Linhas com tamanhos diferentes");
}
data = values;
}
}
/**
* @brief Fornece acesso não constante a um elemento da matriz.
* @param i Índice da linha.
* @param j Índice da coluna.
* @return Referência ao elemento na posição (i, j).
* @throws std::out_of_range Se os índices estiverem fora dos limites.
*/
T& at(size_t i, size_t j) {
if (i >= rows || j >= cols) throw std::out_of_range("Índices fora dos limites da matriz");
return data[i][j];
}
/**
* @brief Fornece acesso constante a um elemento da matriz.
* @param i Índice da linha.
* @param j Índice da coluna.
* @return Referência constante ao elemento na posição (i, j).
* @throws std::out_of_range Se os índices estiverem fora dos limites.
*/
const T& at(size_t i, size_t j) const {
if (i >= rows || j >= cols) throw std::out_of_range("Índices fora dos limites da matriz");
return data[i][j];
}
/**
* @brief Retorna o número de linhas.
* @return O número de linhas da matriz.
*/
size_t num_rows() const { return rows; }
/**
* @brief Retorna o número de colunas.
* @return O número de colunas da matriz.
*/
size_t num_cols() const { return cols; }
/**
* @brief Multiplica esta matriz por outra.
* @param other A matriz a ser multiplicada.
* @return A matriz resultante.
* @throws std::invalid_argument Se as dimensões forem incompatíveis.
*/
Matrix<T> operator*(const Matrix<T>& other) const {
if (cols != other.rows) throw std::invalid_argument("Dimensões incompatíveis para multiplicação de matrizes");
Matrix<T> result(rows, other.cols, T{});
for (size_t i = 0; i < rows; ++i) {
for (size_t j = 0; j < other.cols; ++j) {
for (size_t k = 0; k < cols; ++k) {
result.at(i, j) += data[i][k] * other.data[k][j];
}
}
}
return result;
}
/**
* @brief Calcula a transposta da matriz.
* @return A matriz transposta.
*/
Matrix<T> transpose() const {
Matrix<T> result(cols, rows);
for (size_t i = 0; i < rows; ++i) {
for (size_t j = 0; j < cols; ++j) {
result.at(j, i) = data[i][j];
}
}
return result;
}
/**
* @brief Imprime a matriz com um nome opcional.
* @param name Nome opcional a ser exibido antes da matriz.
*/
void print(const std::string& name = "") const {
if (!name.empty()) std::cout << name << " =\n";
for (size_t i = 0; i < rows; ++i) {
std::cout << "[";
for (size_t j = 0; j < cols; ++j) {
std::cout << std::fixed << std::setprecision(2) << data[i][j];
if (j < cols - 1) std::cout << ", ";
}
std::cout << "]\n";
}
}
/**
* @brief Extrai o valor escalar de uma matriz 1x1.
* @return O valor escalar.
* @throws std::logic_error Se a matriz não for 1x1.
*/
T scalar_value() const {
if (rows != 1 || cols != 1) throw std::logic_error("A matriz não é 1x1");
return data[0][0];
}
/**
* @brief Cria uma matriz coluna a partir de um MathVector.
* @param vec O vetor de entrada.
* @return Uma matriz com o vetor como uma única coluna.
*/
static Matrix<T> column_vector_from(const MathVector<T>& vec) {
Matrix<T> result(vec.dimensions(), 1);
for (size_t i = 0; i < vec.dimensions(); ++i) {
result.at(i, 0) = vec[i];
}
return result;
}
/**
* @brief Cria uma matriz linha a partir de um MathVector.
* @param vec O vetor de entrada.
* @return Uma matriz com o vetor como uma única linha.
*/
static Matrix<T> row_vector_from(const MathVector<T>& vec) {
Matrix<T> result(1, vec.dimensions());
for (size_t i = 0; i < vec.dimensions(); ++i) {
result.at(0, i) = vec[i];
}
return result;
}
};
/**
* @brief Função principal que demonstra operações de produto escalar e baseadas em matrizes.
*
* Este programa ilustra o uso da classe MathVector para calcular produtos escalares diretamente
* e através de representações matriciais, além de demonstrar a extração de componentes e a
* interpretação geométrica do produto escalar com vetores similares, ortogonais e opostos.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
std::cout << std::fixed << std::setprecision(4);
std::cout << "Demonstração de Produto Escalar e Interpretação usando MathVector\n";
std::cout << "-------------------------------------------------------------------\n\n";
MathVector<double> a = {2.0, 5.0, 1.0}; ///< Vetor a para demonstração.
MathVector<double> b = {3.0, 1.0, 4.0}; ///< Vetor b para demonstração.
print_mathvector(a, "Vetor a");
print_mathvector(b, "Vetor b");
// Produto escalar direto
std::cout << "\nCálculo principal via a.dot(b):\n";
double dot_value_direct = a.dot(b);
std::cout << "a · b = " << dot_value_direct << "\n";
// Produto escalar baseado em matriz
std::cout << "\nVisão Alternativa: Representação Matricial (a^T * b):\n";
try {
auto a_row = Matrix<double>::row_vector_from(a);
auto b_col = Matrix<double>::column_vector_from(b);
a_row.print("a como vetor linha (a^T)");
b_col.print("b como vetor coluna (b)");
auto dot_result_matrix = a_row * b_col;
dot_result_matrix.print("\nProduto (a^T * b)");
double dot_value_matrix = dot_result_matrix.scalar_value();
std::cout << "Valor do produto escalar (via matriz): " << dot_value_matrix << "\n";
std::cout << "Verificação manual: " << (a[0]*b[0] + a[1]*b[1] + a[2]*b[2]) << "\n";
} catch (const std::exception& e) {
std::cerr << "Erro na representação matricial: " << e.what() << '\n';
}
// Extração de componente usando produto escalar
std::cout << "\nExemplo 2: Extração da segunda componente de [0.2, 0.7, 0.1] usando dot product\n";
MathVector<double> base_extract = {0.0, 1.0, 0.0}; ///< Vetor base para extração da segunda dimensão.
MathVector<double> data_vec = {0.2, 0.7, 0.1}; ///< Vetor de dados para extração.
print_mathvector(base_extract, "Vetor base (ativa 2a dim)");
print_mathvector(data_vec, "Vetor de dados");
double extracted_value = base_extract.dot(data_vec);
std::cout << "Resultado da extração (base · data): " << extracted_value << "\n";
std::cout << "Verificação: data[1] = " << data_vec[1] << "\n";
// Interpretação geométrica do produto escalar
std::cout << "\nExemplo 3: Interpretação geométrica do produto escalar\n";
// Vetores similares
MathVector<double> v_sim1 = {0.8, 0.6}; ///< Primeiro vetor similar.
MathVector<double> v_sim2 = {0.9, 0.5}; ///< Segundo vetor similar.
print_mathvector(v_sim1, "v_sim1");
print_mathvector(v_sim2, "v_sim2");
std::cout << "Produto escalar (similares): " << v_sim1.dot(v_sim2) << " (positivo)\n\n";
// Vetores ortogonais
MathVector<double> v_ort1 = {1.0, 0.0}; ///< Primeiro vetor ortogonal.
MathVector<double> v_ort2 = {0.0, 1.0}; ///< Segundo vetor ortogonal.
print_mathvector(v_ort1, "v_ort1");
print_mathvector(v_ort2, "v_ort2");
std::cout << "Produto escalar (ortogonais): " << v_ort1.dot(v_ort2) << " (zero)\n\n";
// Vetores opostos
MathVector<double> v_op1 = {0.7, 0.3}; ///< Primeiro vetor oposto.
MathVector<double> v_op2 = {-0.7, -0.3}; ///< Segundo vetor oposto.
print_mathvector(v_op1, "v_op1");
print_mathvector(v_op2, "v_op2");
std::cout << "Produto escalar (opostos): " << v_op1.dot(v_op2) << " (negativo)\n";
return 0;
}
O Produto Escalar e a Similaridade
O produto escalar oferece uma medida quantitativa da similaridade direcional entre dois vetores. Embora não constitua uma métrica de similaridade completa em todos os contextos, fornece informações valiosas sobre o alinhamento vetorial. Em termos gerais, a interpretação do produto escalar $\vec{u} \cdot \vec{v}$ segue estas propriedades:
\[\vec{u} \cdot \vec{v} = \vert \vec{u} \vert \vert \vec{v} \vert \cdot \cos(\theta)\]Onde $\theta$ representa o ângulo entre os vetores, e podemos observar que:
- $\vec{u} \cdot \vec{v} > 0$: Os vetores apontam em direções geralmente similares (ângulo agudo). Quanto maior o valor positivo, maior a similaridade em termos de direção e magnitude das componentes que se alinham.
- $\vec{u} \cdot \vec{v} = 0$: Os vetores são ortogonais (perpendiculares). Não há similaridade direcional linear entre eles.
- $\vec{u} \cdot \vec{v} < 0$: Os vetores apontam em direções geralmente opostas (ângulo obtuso). Quanto mais negativo, maior a dissimilaridade direcional.
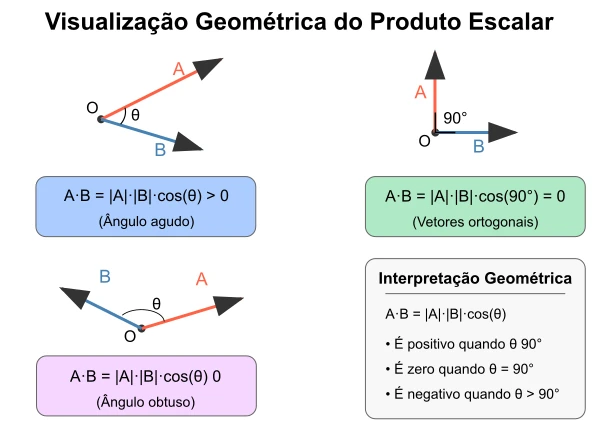
Para vetores normalizados (de magnitude unitária), o produto escalar se reduz diretamente ao cosseno do ângulo entre eles, fornecendo uma medida de similaridade no intervalo $[-1, 1]$, frequentemente utilizada em sistemas de recuperação de informação e processamento de linguagem natural.
Exemplo 2: considerando os vetores $\vec{a} = [0, 1, 0]$ e $\vec{b} = [0.2, 0.7, 0.1]$, o produto escalar será:
\[\vec{a} \cdot \vec{b} = (0 \times 0.2) + (1 \times 0.7) + (0 \times 0.1)\] \[\vec{a} \cdot \vec{b} = 0 + 0.7 + 0 = 0.7\]No exemplo 2, o vetor $\vec{a} = [0, 1, 0]$ pode ser visto como um vetor que ativa, ou dá peso máximo, apenas à segunda dimensão, e peso zero às demais. Ao calcular o produto escalar com $\vec{b} = [0.2, 0.7, 0.1]$, estamos essencialmente extraindo ou medindo o valor da segunda componente de $b$ (que é $0.7$), ponderado pela importância, ou peso que o vetor $a$ atribui a essa dimensão.
Com um pouco mais de formalidade: se temos dois vetores $\vec{u}$ e $\vec{v}$, e você calcula $\vec{u} \cdot \vec{v} = c$, o valor escalar $c$ pode ser interpretado como uma medida de:
- Quanto de $\vec{v}$ “existe” na direção de $\vec{u}$ (e vice-versa);
- O grau de alinhamento ou sobreposição entre os vetores;
- A similaridade entre os padrões representados pelos vetores, no sentido de que componentes importantes em um vetor também são relevantes no outro, com pesos proporcionais aos valores das componentes.
A criativa leitora deve notar que o produto escalar é influenciado tanto pela direção quanto pela magnitude dos vetores.
A magnitude de um vetor é dada pela raiz quadrada da soma dos quadrados dos seus componentes. Isso é equivalente a tirar a raiz quadrada do resultado do produto escalar do vetor com ele mesmo. Para um vetor
\[\vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}\]em um espaço $n$-dimensional, a magnitude, eventualmente chamada de Norma Euclidiana, representada por $ \vert \vec{v} \vert $ será definida por:
\[\vert \vec{v} \vert = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2} = \sqrt{\sum_{i=1}^{n} v_i^2}\]
Exemplo 3: dado o vetor $\vec{b} = \begin{bmatrix} 0.2 \ 0.7 \ 0.1 \end{bmatrix}$, vamos calcular sua magnitude $ \vert \vec{b} \vert $:
Podemos resolver este problema em dois passos:
-
Calcular o produto escalar de $\vec{b}$ consigo mesmo:
\[\vec{b} \cdot \vec{b} = (0.2 \times 0.2) + (0.7 \times 0.7) + (0.1 \times 0.1)\] \[\vec{b} \cdot \vec{b} = 0.04 + 0.49 + 0.01 = 0.54\] -
Extrair a raiz quadrada do resultado:
\[\vert \vec{b} \vert = \sqrt{\vec{b} \cdot \vec{b}} = \sqrt{0.54} \approx 0.7348\]
Portanto, a magnitude do vetor $\vec{b} = \begin{bmatrix} 0.2 \ 0.7 \ 0.1 \end{bmatrix}$ é aproximadamente 0.7348.
A magnitude, pode ter interpretações diferentes em áreas diferentes do conhecimento. Na física, pode representar a intensidade de uma força, ou uma velocidade. No estudo da linguagem natural, a magnitude de um vetor, pode indicar o tamanho do documento em termos de número de palavras, embora não diretamente.
A atenta leitora deve observar que vetores com magnitudes maiores tendem a ter produtos escalares maiores, mesmo que a direção relativa seja a mesma.
Com as definições de produto escalar ($\vec{u} \cdot \vec{v}$) e magnitude ($ \vert \vec{u} \vert $, $ \vert \vec{v} \vert $) em mãos, podemos reorganizar a relação fundamental $\vec{u} \cdot \vec{v} = \vert \vec{u} \vert \cdot \vert \vec{v} \vert \cdot \cos(\theta)$ para isolar o cosseno do ângulo $\theta$. Isso nos fornece diretamente a fórmula da Similaridade de Cosseno, uma das métricas mais importantes em processamento de linguagem natural e recuperação de informação para medir a similaridade direcional entre dois vetores:
\[\text{Similaridade de Cosseno}(\vec{u}, \vec{v}) = \cos(\theta) = \frac{\vec{u} \cdot \vec{v}}{ \vert \vec{u} \vert \vert \vec{v} \vert }\]Esta métrica varia no intervalo $[-1, 1]$:
- $1$: Indica que os vetores apontam exatamente na mesma direção (ângulo $0^\circ$).
- $0$: Indica que os vetores são ortogonais (perpendiculares, ângulo $90^\circ$).
- $-1$: Indica que os vetores apontam em direções exatamente opostas (ângulo $180^\circ$).
A grande vantagem da Similaridade de Cosseno é que ela foca puramente na direção dos vetores, ignorando suas magnitudes. Isso é particularmente útil ao comparar documentos de tamanhos diferentes ou word embeddings, onde a orientação no espaço semântico é mais importante que a magnitude absoluta do vetor.
Quando estudamos processamento de linguagem natural, a magnitude por si não costuma ser a informação mais importante, ou mais buscada. Geralmente estamos interessados na direção de vetores e na similaridade entre eles.
A similaridade entre vetores é uma medida de quão semelhantes são dois vetores em termos de direção e magnitude. Essa medida é fundamental em muitas aplicações, como recuperação de informação, recomendação de produtos e análise de sentimentos.
Em alguns casos, a busca da similaridade implica na normalização dos vetores para que a medida de similaridade seja mais afetada pela direção e menos afetada pela magnitude.
A normalização de um vetor $\vec{v}$ consiste em dividi-lo por sua norma (ou magnitude), resultando em um vetor unitário $\hat{v}$ que mantém a mesma direção, mas possui comprimento 1:
\[\hat{v} = \frac{\vec{v}}{ \vert \vec{v} \vert } = \frac{\vec{v}}{\sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}}\]Neste caso, $ \vert \vec{v} \vert $ representa a norma euclidiana do vetor. Quando dois vetores normalizados são comparados através do produto escalar, o resultado varia apenas entre $-1$ e $1$, correspondendo diretamente ao cosseno do ângulo entre eles. Esta abordagem é particularmente útil em aplicações como recuperação de informações, sistemas de recomendação e processamento de linguagem natural, onde a orientação semântica dos vetores é geralmente mais relevante que suas magnitudes absolutas.
A norma euclidiana, também conhecida como norma $L_2$ ou comprimento euclidiano, é uma função que atribui a cada vetor um valor escalar não-negativo que pode ser interpretado como o “tamanho” ou “magnitude” do vetor. Para um vetor $\vec{v} = (v_1, v_2, \ldots, v_n)$ em $\mathbb{R}^n$, a norma euclidiana é definida como:
\[\vert \vec{v} \vert = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2} = \sqrt{\sum_{i=1}^{n} v_i^2}\]Esta definição é uma generalização do teorema de Pitágoras para espaços de dimensão arbitrária. Geometricamente, representa a distância do ponto representado pelo vetor à origem do sistema de coordenadas.
A norma euclidiana possui as seguintes propriedades fundamentais:
- Não-negatividade: $ \vert \vec{v} \vert \geq 0$ para todo $\vec{v}$, e $ \vert \vec{v} \vert = 0$ se e somente se $\vec{v} = \vec{0}$
- Homogeneidade: $ \vert \alpha\vec{v} \vert = \vert \alpha \vert \cdot \vert \vec{v} \vert $ para qualquer escalar $\alpha$
- Desigualdade triangular: $ \vert \vec{u} + \vec{v} \vert \leq \vert \vec{u} \vert + \vert \vec{v} \vert $
Estas propriedades fazem da norma euclidiana uma ferramenta essencial em diversos campos, desde geometria e física até aprendizado de máquina e processamento de sinais, onde é utilizada para medir distâncias, calcular erros, e normalizar vetores.
Técnicas como a Similaridade de Cosseno, que envolve o produto escalar normalizado pelas magnitudes do vetores, são usadas para isolar a similaridade direcional. Todavia, existem diversas técnicas diferentes para a determinação de um índice para a similaridade entre vetores. Entre elas destacaremos:
-
Distância Euclidiana: mede a distância “direta” entre dois pontos no espaço euclidiano. É sensível tanto à direção quanto à magnitude dos vetores.
-
Distância de Manhattan: também conhecida como distância $L1$, mede a soma das diferenças absolutas das coordenadas dos vetores.
-
Distância de Minkowski: uma generalização das distâncias Euclidiana e de Manhattan, onde a ordem pode ser ajustada para diferentes tipos de distâncias.
-
Similaridade de Jaccard: usada principalmente para conjuntos, mede a similaridade como a razão do tamanho da interseção para o tamanho da união dos conjuntos.
-
Correlação de Pearson: mede a correlação linear entre dois vetores, variando de $-1$ a $1$. É útil para entender a relação linear entre os componentes dos vetores.
-
Distância de Mahalanobis: considera a correlação entre variáveis e é útil quando os vetores têm diferentes escalas ou distribuições.
Algumas já foram usadas processamento de linguagem natural. Outras ainda não. Vamos trabalhar com cada uma delas se, e quando, forem usadas nos algoritmos que estudaremos. A primeira que usaremos será a Similaridade de Cosseno. Mas antes, precisamos entender como representar textos como vetores. Para isso, vamos começar com a representação mais simples e intuitiva: a Frequência de Termos.
Exemplo de Produto Escalar em C++ 20
#include <iostream> ///< Para entrada e saída padrão (std::cout, std::cerr).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de componentes.
#include <numeric> ///< Para std::inner_product, usado no cálculo do produto escalar.
#include <cmath> ///< Para std::sqrt e std::abs, usados em cálculos de magnitude e distâncias.
#include <concepts> ///< Para std::is_arithmetic_v, usado no conceito Arithmetic.
#include <stdexcept> ///< Para exceções padrão como std::out_of_range e std::invalid_argument.
#include <string> ///< Para std::string e std::to_string, usados na conversão para string.
#include <sstream> ///< Para std::stringstream, usado na formatação de números de ponto flutuante.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <initializer_list> ///< Para suporte a inicialização de vetores com listas inicializadoras.
#include <algorithm> ///< Para std::abs, usado no cálculo da distância de Manhattan.
/**
* @concept Arithmetic
* @brief Conceito para garantir que um tipo é aritmético (integral ou de ponto flutuante).
*
* Restringe os parâmetros de template a tipos aritméticos (por exemplo, int, double, float).
*/
template<typename T>
concept Arithmetic = std::is_arithmetic_v<T>;
/**
* @class MathVector
* @brief Uma classe genérica para representar e manipular vetores matemáticos.
*
* Suporta operações como produto escalar, cálculo de magnitude, normalização e conversão para string.
* Usada como base para cálculos de similaridade entre vetores.
*
* @tparam T O tipo aritmético dos componentes do vetor (por exemplo, int, double).
*/
template<Arithmetic T>
class MathVector {
private:
std::vector<T> components; ///< Armazenamento interno para os componentes do vetor.
static constexpr T epsilon = 1e-9; ///< Constante pequena para comparações de ponto flutuante.
public:
/**
* @brief Construtor padrão que cria um vetor vazio.
*/
MathVector() = default;
/**
* @brief Constrói um vetor a partir de uma lista inicializadora.
* @param init Lista inicializadora contendo os componentes do vetor.
*/
MathVector(std::initializer_list<T> init) : components(init) {}
/**
* @brief Constrói um vetor a partir de um std::vector.
* @param vec O vetor de entrada contendo os componentes.
*/
explicit MathVector(const std::vector<T>& vec) : components(vec) {}
/**
* @brief Constrói um vetor de tamanho especificado com todos os componentes inicializados com um valor.
* @param n O número de componentes.
* @param val O valor inicial para todos os componentes (padrão é T{}).
*/
explicit MathVector(size_t n, T val = T{}) : components(n, val) {}
/**
* @brief Retorna o número de dimensões (componentes) do vetor.
* @return O tamanho do vetor.
*/
size_t dimensions() const {
return components.size();
}
/**
* @brief Fornece acesso não constante a um componente do vetor.
* @param index O índice do componente a acessar.
* @return Referência ao componente no índice especificado.
* @throws std::out_of_range Se o índice estiver fora dos limites.
*/
T& operator[](size_t index) {
if (index >= dimensions()) {
throw std::out_of_range("Índice fora dos limites do vetor");
}
return components[index];
}
/**
* @brief Fornece acesso constante a um componente do vetor.
* @param index O índice do componente a acessar.
* @return Referência constante ao componente no índice especificado.
* @throws std::out_of_range Se o índice estiver fora dos limites.
*/
const T& operator[](size_t index) const {
if (index >= dimensions()) {
throw std::out_of_range("Índice fora dos limites do vetor");
}
return components[index];
}
/**
* @brief Calcula o produto escalar deste vetor com outro.
* @param other O outro vetor para o produto escalar.
* @return O resultado escalar do produto escalar.
* @throws std::invalid_argument Se os vetores tiverem dimensões diferentes.
*/
T dot(const MathVector<T>& other) const {
if (dimensions() != other.dimensions()) {
throw std::invalid_argument("Dimensões diferentes para produto escalar");
}
return std::inner_product(components.begin(), components.end(), other.components.begin(), T(0));
}
/**
* @brief Calcula a magnitude euclidiana (norma L2) do vetor.
* @return A magnitude do vetor.
* @note Para tipos integrais, converte para double para sqrt e converte de volta.
*/
T magnitude() const {
T sum_of_squares = this->dot(*this);
if constexpr (std::is_integral_v<T>) {
return static_cast<T>(std::sqrt(static_cast<double>(sum_of_squares)));
} else {
return std::sqrt(sum_of_squares);
}
}
/**
* @brief Normaliza o vetor para ter comprimento unitário.
* @return Um novo vetor normalizado.
* @throws std::domain_error Se a magnitude do vetor for zero ou próxima de zero.
*/
MathVector<T> normalize() const {
T mag = magnitude();
if (std::abs(mag) < epsilon) {
throw std::domain_error("Não é possível normalizar um vetor de magnitude zero (ou muito próxima de zero)");
}
MathVector<T> result(dimensions());
for (size_t i = 0; i < dimensions(); ++i) {
result[i] = components[i] / mag;
}
return result;
}
/**
* @brief Converte o vetor para uma representação em string.
* @return Uma string representando o vetor (por exemplo, "[1.0000, 2.0000]").
* @note Para tipos de ponto flutuante, usa precisão fixa de 4 casas decimais.
*/
std::string to_string() const {
std::string result = "[";
for (size_t i = 0; i < dimensions(); ++i) {
if constexpr (std::is_floating_point_v<T>) {
std::stringstream ss;
ss << std::fixed << std::setprecision(4) << components[i];
result += ss.str();
} else {
result += std::to_string(components[i]);
}
if (i < dimensions() - 1) {
result += ", ";
}
}
result += "]";
return result;
}
};
/**
* @class VectorSimilarity
* @brief Uma classe para calcular métricas de similaridade e distância entre vetores.
*
* Fornece métodos para produto escalar, similaridade de cosseno, distâncias euclidiana e de Manhattan,
* e normalização de vetores, com verificações robustas de dimensões e magnitude.
*
* @tparam T O tipo aritmético dos componentes do vetor (por exemplo, int, double).
*/
template<Arithmetic T>
class VectorSimilarity {
private:
static constexpr T epsilon = 1e-9; ///< Constante pequena para comparações de ponto flutuante.
/**
* @brief Verifica se dois vetores têm a mesma dimensão.
* @param a Primeiro vetor.
* @param b Segundo vetor.
* @return true se as dimensões forem iguais, false caso contrário.
*/
static bool check_dimensions(const MathVector<T>& a, const MathVector<T>& b) {
return a.dimensions() == b.dimensions();
}
public:
/**
* @brief Calcula o produto escalar entre dois vetores.
* @param a Primeiro vetor.
* @param b Segundo vetor.
* @return O resultado escalar do produto escalar.
* @throws std::invalid_argument Se os vetores tiverem dimensões diferentes.
*/
static T dot_product(const MathVector<T>& a, const MathVector<T>& b) {
return a.dot(b);
}
/**
* @brief Calcula a similaridade de cosseno entre dois vetores.
* @param a Primeiro vetor.
* @param b Segundo vetor.
* @return O valor da similaridade de cosseno, no intervalo [-1, 1].
* @throws std::invalid_argument Se os vetores tiverem dimensões diferentes.
* @throws std::domain_error Se a magnitude de qualquer vetor for zero ou próxima de zero.
*/
static T cosine_similarity(const MathVector<T>& a, const MathVector<T>& b) {
if (!check_dimensions(a, b)) {
throw std::invalid_argument("Vetores com dimensões diferentes para similaridade de cosseno");
}
T mag_a = a.magnitude();
T mag_b = b.magnitude();
if (std::abs(mag_a) < epsilon || std::abs(mag_b) < epsilon) {
throw std::domain_error("Magnitude zero (ou próxima) em cálculo de similaridade de cosseno");
}
T dot = a.dot(b);
return dot / (mag_a * mag_b);
}
/**
* @brief Calcula a distância euclidiana entre dois vetores.
* @param a Primeiro vetor.
* @param b Segundo vetor.
* @return A distância euclidiana (norma L2 da diferença).
* @throws std::invalid_argument Se os vetores tiverem dimensões diferentes.
*/
static T euclidean_distance(const MathVector<T>& a, const MathVector<T>& b) {
if (!check_dimensions(a, b)) {
throw std::invalid_argument("Vetores com dimensões diferentes para distância euclidiana");
}
T sum_of_squares = 0;
for (size_t i = 0; i < a.dimensions(); ++i) {
T diff = a[i] - b[i];
sum_of_squares += diff * diff;
}
if constexpr (std::is_integral_v<T>) {
return static_cast<T>(std::sqrt(static_cast<double>(sum_of_squares)));
} else {
return std::sqrt(sum_of_squares);
}
}
/**
* @brief Calcula a distância de Manhattan (norma L1) entre dois vetores.
* @param a Primeiro vetor.
* @param b Segundo vetor.
* @return A distância de Manhattan (soma das diferenças absolutas).
* @throws std::invalid_argument Se os vetores tiverem dimensões diferentes.
*/
static T manhattan_distance(const MathVector<T>& a, const MathVector<T>& b) {
if (!check_dimensions(a, b)) {
throw std::invalid_argument("Vetores com dimensões diferentes para distância de Manhattan");
}
T sum_of_abs_diff = 0;
for (size_t i = 0; i < a.dimensions(); ++i) {
sum_of_abs_diff += std::abs(a[i] - b[i]);
}
return sum_of_abs_diff;
}
/**
* @brief Normaliza um vetor para ter magnitude unitária.
* @param vec O vetor a ser normalizado.
* @return Um novo vetor normalizado.
* @throws std::domain_error Se a magnitude do vetor for zero ou próxima de zero.
*/
static MathVector<T> normalize(const MathVector<T>& vec) {
return vec.normalize();
}
};
/**
* @brief Imprime um MathVector com um nome especificado.
* @tparam T O tipo aritmético dos componentes do vetor.
* @param vec O vetor a ser impresso.
* @param name O nome a ser exibido ao lado do vetor.
*/
template<Arithmetic T>
void print_mathvector(const MathVector<T>& vec, const std::string& name) {
std::cout << name << " = " << vec.to_string() << "\n";
}
/**
* @brief Função principal que demonstra cálculos de similaridade e distância entre vetores.
*
* Este programa ilustra o uso da classe VectorSimilarity para calcular o produto escalar,
* similaridade de cosseno, distâncias euclidiana e de Manhattan, e normalização de vetores.
* Inclui exemplos com vetores alinhados, ortogonais, opostos, extração de componentes,
* e normalização, com tratamento de erros robusto.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
std::cout << std::fixed << std::setprecision(4);
std::cout << "Demonstração de Cálculos de Similaridade e Distância entre Vetores\n";
std::cout << "-----------------------------------------------------------------\n\n";
// Exemplo 1: Vetores alinhados (similares)
std::cout << "Exemplo 1: Vetores geralmente alinhados (similares)\n";
MathVector<double> u1 = {0.5, 0.8, 0.3}; ///< Primeiro vetor similar.
MathVector<double> v1 = {0.6, 0.9, 0.2}; ///< Segundo vetor similar.
try {
print_mathvector(u1, "Vetor u1");
print_mathvector(v1, "Vetor v1");
std::cout << "Produto escalar: " << VectorSimilarity<double>::dot_product(u1, v1) << "\n";
std::cout << "Similaridade de cosseno: " << VectorSimilarity<double>::cosine_similarity(u1, v1) << "\n";
std::cout << "Distância euclidiana: " << VectorSimilarity<double>::euclidean_distance(u1, v1) << "\n";
std::cout << "Distância de Manhattan: " << VectorSimilarity<double>::manhattan_distance(u1, v1) << "\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
// Exemplo 2: Vetores ortogonais (perpendiculares)
std::cout << "\nExemplo 2: Vetores ortogonais (perpendiculares)\n";
MathVector<double> u2 = {1.0, 0.0, 0.0}; ///< Primeiro vetor ortogonal.
MathVector<double> v2 = {0.0, 1.0, 0.0}; ///< Segundo vetor ortogonal.
try {
print_mathvector(u2, "Vetor u2");
print_mathvector(v2, "Vetor v2");
std::cout << "Produto escalar: " << VectorSimilarity<double>::dot_product(u2, v2) << "\n";
std::cout << "Similaridade de cosseno: " << VectorSimilarity<double>::cosine_similarity(u2, v2) << "\n";
std::cout << "Distância euclidiana: " << VectorSimilarity<double>::euclidean_distance(u2, v2) << "\n";
std::cout << "Distância de Manhattan: " << VectorSimilarity<double>::manhattan_distance(u2, v2) << "\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
// Exemplo 3: Vetores em direções opostas
std::cout << "\nExemplo 3: Vetores em direções opostas\n";
MathVector<double> u3 = {0.7, 0.2, -0.3}; ///< Primeiro vetor oposto.
MathVector<double> v3 = {-0.7, -0.2, 0.3}; ///< Segundo vetor oposto.
try {
print_mathvector(u3, "Vetor u3");
print_mathvector(v3, "Vetor v3");
std::cout << "Produto escalar: " << VectorSimilarity<double>::dot_product(u3, v3) << "\n";
std::cout << "Similaridade de cosseno: " << VectorSimilarity<double>::cosine_similarity(u3, v3) << "\n";
std::cout << "Distância euclidiana: " << VectorSimilarity<double>::euclidean_distance(u3, v3) << "\n";
std::cout << "Distância de Manhattan: " << VectorSimilarity<double>::manhattan_distance(u3, v3) << "\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
// Exemplo 4: Extração de componente usando produto escalar
std::cout << "\nExemplo 4: Extração de componente usando produto escalar\n";
MathVector<double> base = {0.0, 1.0, 0.0}; ///< Vetor base para extração da segunda dimensão.
MathVector<double> data = {0.2, 0.7, 0.1}; ///< Vetor de dados para extração.
try {
print_mathvector(base, "Vetor base");
print_mathvector(data, "Vetor data");
double extracted = VectorSimilarity<double>::dot_product(base, data);
std::cout << "Produto escalar (extrai valor): " << extracted << "\n";
std::cout << "Verificação: data[1] = " << data[1] << "\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
// Exemplo 5: Normalização de vetor
std::cout << "\nExemplo 5: Normalização de vetor\n";
MathVector<double> original = {0.2, 0.7, 0.1}; ///< Vetor a ser normalizado.
try {
print_mathvector(original, "Vetor original");
MathVector<double> normalized = VectorSimilarity<double>::normalize(original);
print_mathvector(normalized, "Vetor normalizado");
std::cout << "Magnitude do vetor original: " << original.magnitude() << "\n";
std::cout << "Magnitude do vetor normalizado: " << normalized.magnitude() << "\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
return 0;
}
Agora que conhecemos o produto escalar, podemos nos aprofundar na matemática que é o coração do processamento de linguagem natural: a multiplicação de matrizes.
Multiplicação de Matrizes
A multiplicação de matrizes é uma operação fundamental na álgebra linear que aparece constantemente nos modelos de transformers. Esta operação irá permitir a combinação de diferentes fontes de textos e transformar representações vetoriais, formando a base de diversas operações nos modelos de processamento de linguagem natural.
A multiplicação de matrizes é uma operação que combina duas matrizes para produzir uma nova matriz. É importante notar que a multiplicação de matrizes não é comutativa, ou seja, a ordem das matrizes importa. A multiplicação de matrizes é definida como o produto escalar entre as linhas da primeira matriz e as colunas da segunda matriz.
Formalmente dizemos: sejam $A$ uma matriz de dimensão $m \times n$ e $B$ uma matriz de dimensão $n \times p$. O produto $A \times B$ resultará em uma matriz $C$ de dimensão $m \times p$, onde cada elemento $c_{ij}$ é determinado pelo produto escalar da $i$-ésima linha de $A$ com a $j$-ésima coluna de $B$:
\[c_{ij} = \sum_{k=1}^{n} a_{ik} \cdot b_{kj}\]Observe, atenta leitora, que para que a multiplicação de matrizes seja possível, o número de colunas da primeira matriz deve ser igual ao número de linhas da segunda matriz. Esta restrição não é arbitrária - ela garante que os produtos escalares entre linhas e colunas sejam bem definidos.
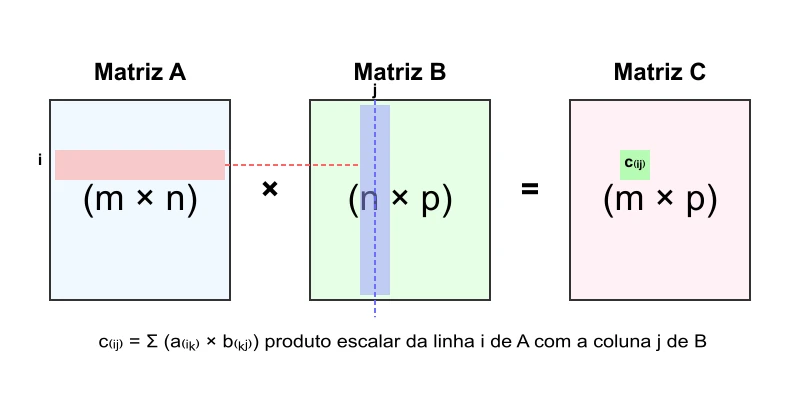
Figura 3: Visualização da multiplicação de matrizes.
Cada elemento $c_{ij}$ da matriz resultante é obtido pelo produto escalar da linha $i$ da matriz $A$ com a coluna $j$ da matriz $B$.
Nos modelos transformer, a multiplicação de matrizes ocorre com frequência em várias etapas, como:
- Atenção: O mecanismo de atenção utiliza multiplicações de matrizes para calcular as representações de query, key e value;
- Embedding de Tokens: Transformação de tokens discretos em vetores contínuos de alta dimensão;
- Projeções Lineares: Transformações dos vetores de query, key e value no mecanismo de atenção;
- Feed-Forward Networks: Camadas densas que aplicam transformações não-lineares às representações;
- Projeções de Saída: Mapeamento das representações finais para o espaço de saída desejado.
A eficiência dos modelos transformers deve-se, em parte, à capacidade de paralelizar estas multiplicações de matrizes em hardware especializado, como GPUs e TPUs.
Finalmente, a esforçada leitora deve observar que estudamos multiplicação de matrizes com mais profundidade neste artigo.
Propriedades Importantes
A multiplicação de matrizes possui algumas propriedades notáveis que a diferenciam da multiplicação de números reais:
- Não comutativa: em geral, $A \times B \neq B \times A$. A ordem das operações importa.
- Associativa: $(A \times B) \times C = A \times (B \times C)$. Podemos calcular multiplicações sucessivas em qualquer ordem.
- Distributiva sobre a adição: $A \times (B + C) = A \times B + A \times C$.
- Elemento neutro: $A \times I = I \times A = A$, onde $I$ é a matriz identidade de dimensão apropriada.
Interpretação Geométrica
Geometricamente, a multiplicação por uma matriz pode ser vista como uma transformação linear no espaço vetorial. Estas transformações podem incluir: rotações, mudança de escala, reflexões, cisalhamentos e projeções. Dependendo da matriz, a transformação pode alterar a posição, a forma ou a orientação dos vetores no espaço.
Nos transformers, estas transformações são aplicadas para mapear representações vetoriais de um espaço para outro, permitindo que a rede aprenda relações complexas entre os elementos da sequência de entrada.
Exemplo Numérico
Nada como um exemplo numérico para fazer a esforçada leitora balançar a poeira. Vamos consider as duas matrizes, $A$ e $B$:
\[A = \begin{bmatrix} 2 & 3 \\ 4 & 1 \end{bmatrix} \quad \text{e} \quad B = \begin{bmatrix} 1 & 5 \\ 2 & 3 \end{bmatrix}\]O produto $C = A \times B$ será:
\[\begin{align} c_{11} &= a_{11} \cdot b_{11} + a_{12} \cdot b_{21} = 2 \times 1 + 3 \times 2 = 2 + 6 = 8 \\ c_{12} &= a_{11} \cdot b_{12} + a_{12} \cdot b_{22} = 2 \times 5 + 3 \times 3 = 10 + 9 = 19 \\ c_{21} &= a_{21} \cdot b_{11} + a_{22} \cdot b_{21} = 4 \times 1 + 1 \times 2 = 4 + 2 = 6 \\ c_{22} &= a_{21} \cdot b_{12} + a_{22} \cdot b_{22} = 4 \times 5 + 1 \times 3 = 20 + 3 = 23 \end{align}\]Portanto:
\[C = A \times B = \begin{bmatrix} 8 & 19 \\ 6 & 23 \end{bmatrix}\]Multiplicação Matriz-Vetor
Um caso especial e extremamente importante, para nossos objetivos, é a multiplicação de uma matriz por um vetor. A perceptiva leitora há de considerar que um vetor que pode ser visto como uma matriz com apenas uma coluna. Esta operação é recorrente em praticamente todas as camadas de um modelo transformer.
Seja $A$ uma matriz $m \times n$ e $\vec{v}$ um vetor coluna de dimensão $n$. O produto $A\vec{v}$ resulta em um vetor coluna $\vec{w}$ de dimensão $m$:
\[\vec{w} = A\vec{v} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} = \begin{bmatrix} \sum_{j=1}^{n} a_{1j}v_j \\ \sum_{j=1}^{n} a_{2j}v_j \\ \vdots \\ \sum_{j=1}^{n} a_{mj}v_j \end{bmatrix}\]Cada componente $w_i$ do vetor resultante é o produto escalar da $i$-ésima linha da matriz $A$ com o vetor $\vec{v}$. Este padrão de operação repete-se continuamente no mecanismo de atenção dos transformers.
Exemplo: Considerando a matriz $A$ definida acima e o vetor $\vec{v} = \begin{bmatrix} 3 \ 2 \end{bmatrix}$, temos:
\[A\vec{v} = \begin{bmatrix} 2 & 3 \\ 4 & 1 \end{bmatrix} \begin{bmatrix} 3 \\ 2 \end{bmatrix} = \begin{bmatrix} (2 \times 3) + (3 \times 2) \\ (4 \times 3) + (1 \times 2) \end{bmatrix} = \begin{bmatrix} 6 + 6 \\ 12 + 2 \end{bmatrix} = \begin{bmatrix} 12 \\ 14 \end{bmatrix}\]Exemplo de Operações de Multiplicação de Matrizes em C++ 20
#include <iostream> ///< Para entrada e saída padrão (std::cout, std::cerr).
#include <vector> ///< Para contêiner std::vector usado no armazenamento de elementos da matriz.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <stdexcept> ///< Para exceções padrão como std::out_of_range e std::invalid_argument.
/**
* @class Matrix
* @brief Uma classe genérica para representar e manipular matrizes.
*
* Suporta operações como multiplicação de matrizes, multiplicação por vetor e impressão formatada.
* A matriz é armazenada como um vetor de vetores de tipo T.
*
* @tparam T O tipo dos elementos da matriz (deve suportar operações aritméticas).
*/
template<typename T>
class Matrix {
private:
std::vector<std::vector<T>> data; ///< Armazenamento interno para os elementos da matriz.
size_t rows; ///< Número de linhas da matriz.
size_t cols; ///< Número de colunas da matriz.
public:
/**
* @brief Construtor para criar uma matriz de dimensões m x n com valor inicial.
* @param m Número de linhas.
* @param n Número de colunas.
* @param initial_value Valor inicial para todos os elementos (padrão é T{}).
*/
Matrix(size_t m, size_t n, T initial_value = T{})
: rows(m), cols(n), data(m, std::vector<T>(n, initial_value)) {}
/**
* @brief Construtor a partir de um vetor de vetores.
* @param values Os dados de entrada como um vetor de vetores.
* @throws std::invalid_argument Se as linhas tiverem tamanhos inconsistentes.
*/
Matrix(const std::vector<std::vector<T>>& values) {
if (values.empty()) {
rows = 0;
cols = 0;
return;
}
rows = values.size();
cols = values[0].size();
// Verifica se todas as linhas têm o mesmo tamanho
for (const auto& row : values) {
if (row.size() != cols) {
throw std::invalid_argument("Todas as linhas devem ter o mesmo número de colunas");
}
}
data = values; // Copia os dados
}
/**
* @brief Fornece acesso não constante a um elemento da matriz.
* @param i Índice da linha.
* @param j Índice da coluna.
* @return Referência ao elemento na posição (i, j).
* @throws std::out_of_range Se os índices estiverem fora dos limites.
*/
T& at(size_t i, size_t j) {
if (i >= rows || j >= cols) {
throw std::out_of_range("Índices fora dos limites da matriz");
}
return data[i][j];
}
/**
* @brief Fornece acesso constante a um elemento da matriz.
* @param i Índice da linha.
* @param j Índice da coluna.
* @return Referência constante ao elemento na posição (i, j).
* @throws std::out_of_range Se os índices estiverem fora dos limites.
*/
const T& at(size_t i, size_t j) const {
if (i >= rows || j >= cols) {
throw std::out_of_range("Índices fora dos limites da matriz");
}
return data[i][j];
}
/**
* @brief Retorna o número de linhas da matriz.
* @return O número de linhas.
*/
size_t num_rows() const { return rows; }
/**
* @brief Retorna o número de colunas da matriz.
* @return O número de colunas.
*/
size_t num_cols() const { return cols; }
/**
* @brief Multiplica esta matriz por outra.
* @param other A matriz a ser multiplicada.
* @return A matriz resultante.
* @throws std::invalid_argument Se as dimensões forem incompatíveis.
*/
Matrix<T> operator*(const Matrix<T>& other) const {
if (cols != other.rows) {
throw std::invalid_argument("Dimensões incompatíveis para multiplicação de matrizes");
}
Matrix<T> result(rows, other.cols, T{});
for (size_t i = 0; i < rows; ++i) {
for (size_t j = 0; j < other.cols; ++j) {
for (size_t k = 0; k < cols; ++k) {
result.data[i][j] += data[i][k] * other.data[k][j];
}
}
}
return result;
}
/**
* @brief Multiplica a matriz por um vetor (representado como matriz coluna).
* @param vec O vetor de entrada.
* @return O vetor resultante da multiplicação.
* @throws std::invalid_argument Se as dimensões forem incompatíveis.
*/
std::vector<T> multiply_vector(const std::vector<T>& vec) const {
if (cols != vec.size()) {
throw std::invalid_argument("Dimensões incompatíveis para multiplicação matriz-vetor");
}
std::vector<T> result(rows, T{});
for (size_t i = 0; i < rows; ++i) {
for (size_t j = 0; j < cols; ++j) {
result[i] += data[i][j] * vec[j];
}
}
return result;
}
/**
* @brief Imprime a matriz formatada com um nome opcional.
* @param name Nome opcional a ser exibido antes da matriz.
*/
void print(const std::string& name = "") const {
if (!name.empty()) {
std::cout << name << " =\n";
}
for (size_t i = 0; i < rows; ++i) {
std::cout << "[";
for (size_t j = 0; j < cols; ++j) {
std::cout << std::fixed << std::setprecision(2) << data[i][j];
if (j < cols - 1) std::cout << ", ";
}
std::cout << "]\n";
}
}
};
/**
* @brief Função principal que demonstra operações de multiplicação de matrizes.
*
* Este programa ilustra a multiplicação de matrizes, a multiplicação de matriz por vetor
* e o tratamento de erros para dimensões incompatíveis usando a classe Matrix.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
std::cout << std::fixed << std::setprecision(2);
std::cout << "Demonstração de Multiplicação de Matrizes\n";
std::cout << "----------------------------------------\n\n";
// Exemplo 1: Multiplicação de duas matrizes
Matrix<double> A({
{2.0, 3.0},
{4.0, 1.0}
}); ///< Matriz A (2x2) para demonstração.
Matrix<double> B({
{1.0, 5.0},
{2.0, 3.0}
}); ///< Matriz B (2x2) para demonstração.
std::cout << "Exemplo 1: Multiplicação de duas matrizes\n";
A.print("Matriz A");
B.print("Matriz B");
try {
Matrix<double> C = A * B;
C.print("A * B");
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << '\n';
}
// Exemplo 2: Multiplicação matriz-vetor
std::vector<double> v = {3.0, 2.0}; ///< Vetor v (2x1) para demonstração.
std::cout << "\nExemplo 2: Multiplicação matriz-vetor\n";
A.print("Matriz A");
std::cout << "Vetor v = [" << v[0] << ", " << v[1] << "]\n";
try {
std::vector<double> result = A.multiply_vector(v);
std::cout << "A * v = [";
for (size_t i = 0; i < result.size(); ++i) {
std::cout << result[i];
if (i < result.size() - 1) std::cout << ", ";
}
std::cout << "]\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << '\n';
}
// Exemplo 3: Demonstração de erro (dimensões incompatíveis)
Matrix<double> D({
{1.0, 2.0, 3.0},
{4.0, 5.0, 6.0}
}); ///< Matriz D (2x3) para demonstração de erro.
std::cout << "\nExemplo 3: Tentativa de multiplicação com dimensões incompatíveis\n";
A.print("Matriz A (2x2)");
D.print("Matriz D (2x3)");
try {
Matrix<double> E = D * A; // Isso deve falhar (3 colunas × 2 linhas)
E.print("D * A");
} catch (const std::exception& e) {
std::cout << "Erro (esperado): " << e.what() << '\n';
}
return 0;
}
Ou, como a preocupada leitora pode preferir, em C++ 20 usando a biblioteca Eigen:
#include <iostream> ///< Para entrada e saída padrão (std::cout, std::cerr).
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <Eigen/Dense> ///< Para a biblioteca Eigen, usada em operações de álgebra linear.
#include <string> ///< Para std::string, usada em mensagens de erro.
#include <stdexcept> ///< Para exceções padrão como std::invalid_argument.
/**
* @brief Função principal que demonstra operações de multiplicação de matrizes usando a biblioteca Eigen.
*
* Este programa ilustra três exemplos: a multiplicação de duas matrizes, a multiplicação de uma matriz por um vetor
* e uma tentativa de multiplicação com dimensões incompatíveis, demonstrando o tratamento de erros. As operações são
* realizadas utilizando a biblioteca Eigen, e os resultados são exibidos no console com formatação de duas casas decimais.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
std::cout << std::fixed << std::setprecision(2); ///< Define precisão fixa de duas casas decimais para saída.
std::cout << "Demonstração de Multiplicação de Matrizes\n";
std::cout << "----------------------------------------\n\n";
// Exemplo 1: Multiplicação de duas matrizes
Eigen::Matrix2d A; ///< Matriz A (2x2) para demonstração.
A << 2.0, 3.0,
4.0, 1.0;
Eigen::Matrix2d B; ///< Matriz B (2x2) para demonstração.
B << 1.0, 5.0,
2.0, 3.0;
std::cout << "Exemplo 1: Multiplicação de duas matrizes\n";
std::cout << "Matriz A =\n" << A << "\n\n";
std::cout << "Matriz B =\n" << B << "\n\n";
try {
Eigen::Matrix2d C = A * B; ///< Calcula o produto A * B.
std::cout << "A * B =\n" << C << "\n\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << '\n';
}
// Exemplo 2: Multiplicação matriz-vetor
Eigen::Vector2d v; ///< Vetor v (2x1) para demonstração.
v << 3.0, 2.0;
std::cout << "Exemplo 2: Multiplicação matriz-vetor\n";
std::cout << "Matriz A =\n" << A << "\n\n";
std::cout << "Vetor v =\n" << v << "\n\n";
try {
Eigen::Vector2d result = A * v; ///< Calcula o produto A * v.
std::cout << "A * v =\n" << result << "\n\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << '\n';
}
// Exemplo 3: Demonstração de erro (dimensões incompatíveis)
Eigen::MatrixXd D(2, 3); ///< Matriz D (2x3) para demonstração de erro.
D << 1.0, 2.0, 3.0,
4.0, 5.0, 6.0;
std::cout << "Exemplo 3: Tentativa de multiplicação com dimensões incompatíveis\n";
std::cout << "Matriz A (2x2) =\n" << A << "\n\n";
std::cout << "Matriz D (2x3) =\n" << D << "\n\n";
try {
// Verificação explícita de dimensões (para ser didático)
if (D.cols() != A.rows()) {
throw std::invalid_argument("Dimensões incompatíveis: D é 2x3 e A é 2x2");
}
// Eigen lançará uma asserção estática aqui se compilado com verificações
Eigen::MatrixXd E = D * A; ///< Tentativa de calcular D * A (deve falhar).
std::cout << "D * A =\n" << E << "\n\n";
} catch (const std::exception& e) {
std::cout << "Erro (esperado): " << e.what() << '\n';
}
return 0;
}
Agora que vimos o básico da matemática, a vetorização de textos será o tema do próximo artigo.
Operações de Matrizes Diferenciáveis: Fundamentos e Aplicações
Vou forçar um pouco a amizade. Para entender os transformers a esforçada leitora precisará entender operações diferenciáveis com matrizes. Estas operações são essenciais para entender os mecanismos de aprendizado profundo, cálculo de gradientes e otimização computacional. Todas técnicas são técnicas usadas para implementar os algoritmos que conhecemos como transformers.
As operações de matrizes diferenciáveis são funções que mapeiam matrizes para matrizes, ou para escalares, mantendo propriedades de diferenciabilidade. Em outras palavras, são operações para as quais podemos calcular derivadas ou gradientes. Este conceito é o coração matemático que permite o funcionamento de algoritmos de otimização, particularmente em redes neurais modernas.
Derivada vs. Gradiente
A derivada é um conceito do cálculo que mede a taxa de variação de uma função $f(x)$ de uma única variável. Formalmente, a derivada de $f$ no ponto $x$ é definida como:
\[f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\]O gradiente, por sua vez, é a generalização da derivada para funções de múltiplas variáveis. Para uma função $f(x_1, x_2, …, x_n)$, o gradiente é um vetor cujas componentes são as derivadas parciais da função em relação a cada variável:
\[\nabla f = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n}\right)\]Diferenças fundamentais: a derivada é um escalar, enquanto o gradiente é um vetor. Além disso, a derivada indica a direção e taxa de crescimento em uma dimensão, enquanto o gradiente aponta na direção de máximo crescimento da função no espaço multidimensional. Finalmente, para funções de uma única variável, o gradiente se reduz à derivada comum
O gradiente é particularmente importante em otimização, pois seu oposto indica a direção de descida mais íngreme, fundamental para algoritmos como o gradiente descendente usado no treinamento de modelos de aprendizado de máquina.
Ao contrário de operações discretas, as operações diferenciáveis permitem ajustes contínuos e graduais, essenciais para a convergência de algoritmos de aprendizado. Pense nas operações diferenciáveis como uma bússola matemática que guia o modelo através de um oceano de parâmetros em direção ao mínimo de uma função de perda.
Formalmente, consideremos uma função $f: \mathbb{R}^{m \times n} \rightarrow \mathbb{R}$ que mapeia uma matriz $X \in \mathbb{R}^{m \times n}$ para um escalar. Esta função é diferenciável em um ponto $X$ se existe uma matriz $\nabla f(X) \in \mathbb{R}^{m \times n}$, chamada gradiente de $f$ em $X$, tal que:
\[\lim_{H \rightarrow 0} \frac{f(X + H) - f(X) - \langle \nabla f(X), H \rangle_F}{\|H\|_F} = 0\]Nesta expressão, temos:
- $H$ representa uma perturbação infinitesimal na matriz $X$;
- $\langle A, B \rangle_F = \text{tr}(A^T B)$ é o produto interno de Frobenius entre matrizes;
- $|H|F = \sqrt{\sum{i,j} H_{ij}^2}$ é a norma de Frobenius da matriz $H$.
O produto interno de Frobenius é essencialmente o produto escalar generalizado para matrizes. Se interpretarmos as matrizes $A$ e $B$ como vetores “esticados”, o produto interno de Frobenius é equivalente ao produto escalar desses vetores.
A norma de Frobenius, por sua vez, é a generalização da norma euclidiana para matrizes, e mede a “magnitude” total de uma matriz.
Operações Fundamentais e Suas Derivadas
Vamos examinar as principais operações de matrizes diferenciáveis e suas derivadas correspondentes. Para cada operação, apresentaremos a definição formal, a interpretação intuitiva e exemplos numéricos quando apropriado.
-
Adição de Matrizes: A adição de matrizes é uma operação elementar onde somamos correspondentemente os elementos de duas matrizes de mesmas dimensões. Sejam $A, B \in \mathbb{R}^{m \times n}$, a adição será definida como:
\[f(A, B) = A + B\]Derivadas:
- $\frac{\partial f}{\partial A} = I$ (matriz identidade);
- $\frac{\partial f}{\partial B} = I$ (matriz identidade).
Isto significa que uma pequena mudança em qualquer elemento de $A$ ou $B$ resulta em uma mudança exatamente igual no elemento correspondente da matriz resultante. Esta propriedade reflete a natureza linear e direta da adição.
Exemplo Numérico: considerando $A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}$ e $B = \begin{bmatrix} 5 & 6 \ 7 & 8 \end{bmatrix}$, temos:
\[A + B = \begin{bmatrix} 1+5 & 2+6 \\ 3+7 & 4+8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix}\]Se perturbarmos $A_{11}$ por uma pequena quantidade $\epsilon$, o resultado será alterado exatamente por $\epsilon$ no elemento $(1,1)$.
-
Multiplicação de Matrizes: a multiplicação matricial é uma operação fundamental que combina informações de duas matrizes através de produtos escalares entre linhas e colunas. Sejam $A \in \mathbb{R}^{m \times n}$ e $B \in \mathbb{R}^{n \times p}$, a multiplicação será definida como:
\[f(A, B) = AB\]Derivadas: Para uma matriz resultante $C = AB$, onde $A \in \mathbb{R}^{m \times n}$ e $B \in \mathbb{R}^{n \times p}$:
- $\frac{\partial C_{ij}}{\partial A_{kl}} = B_{lj}$ se $i = k$, e $0$ caso contrário;
- $\frac{\partial C_{ij}}{\partial B_{kl}} = A_{ik}$ se $j = l$, e $0$ caso contrário.
Em notação tensorial mais compacta:
- $\frac{\partial (AB){ij}}{\partial A{kl}} = \delta_{ik} B_{lj}$;
- $\frac{\partial (AB){ij}}{\partial B{kl}} = A_{il} \delta_{jk}$.
Neste caso, $\delta_{ij}$ é o delta de Kronecker, igual a $1$ se $i = j$ e $$0$ caso contrário.
Para que a esforçada leitora possa entender isso considere que o elemento $C_{ij}$ depende de toda a $i$-ésima linha de $A$ e da $j$-ésima coluna de $B$. Uma mudança em $A_{il}$ afetará $C_{ij}$ proporcionalmente a $B_{lj}$.
Exemplo Numérico: considerando $A = \begin{bmatrix} 2 & 3 \ 4 & 1 \end{bmatrix}$ e $B = \begin{bmatrix} 1 & 5 \ 2 & 3 \end{bmatrix}$, temos:
\[AB = \begin{bmatrix} 2 \times 1 + 3 \times 2 & 2 \times 5 + 3 \times 3 \\ 4 \times 1 + 1 \times 2 & 4 \times 5 + 1 \times 3 \end{bmatrix} = \begin{bmatrix} 8 & 19 \\ 6 & 23 \end{bmatrix}\]Se aumentarmos $A_{12}$ (o elemento $3$) por $0.1$, o novo valor será:
\[A = \begin{bmatrix} 2 & 3.1 \\ 4 & 1 \end{bmatrix}\]E o produto atualizado:
\[AB = \begin{bmatrix} 2 \times 1 + 3.1 \times 2 & 2 \times 5 + 3.1 \times 3 \\ 4 \times 1 + 1 \times 2 & 4 \times 5 + 1 \times 3 \end{bmatrix} = \begin{bmatrix} 8.2 & 19.3 \\ 6 & 23 \end{bmatrix}\]Observe que apenas os elementos da primeira linha foram alterados, e a mudança em $C_{11}$ foi de $0.1 \times B_{21} = 0.1 \times 2 = 0.2$, enquanto a mudança em $C_{12}$ foi de $0.1 \times B_{22} = 0.1 \times 3 = 0.3$.
-
Traço de Matriz: o traço de uma matriz quadrada é a soma dos elementos da diagonal principal. É uma operação que reduz uma matriz a um escalar. Seja $A \in \mathbb{R}^{n \times n}$, o traço será definido como:
\[f(A) = \text{tr}(A)\]Derivada:
- $\frac{\partial \text{tr}(A)}{\partial A} = I$ (matriz identidade).
Isto significa que a derivada do traço em relação a cada elemento da diagonal é $1$, e em relação aos elementos fora da diagonal é $0$.
Exemplo Numérico: para $A = \begin{bmatrix} 3 & 2 \ 1 & 5 \end{bmatrix}$, temos $\text{tr}(A) = 3 + 5 = 8$.
Aumentando $A_{11}$ por 0.1, o novo traço será $3.1 + 5 = 8.1$, confirmando que $\frac{\partial \text{tr}(A)}{\partial A_{11}} = 1$.
-
Determinante de Matriz: o determinante é uma função escalar de uma matriz quadrada que tem interpretações geométricas importantes e está relacionado a propriedades como inversibilidade. Seja $A \in \mathbb{R}^{n \times n}$, o determinante será definido como:
\[f(A) = \det(A)\]Derivada:
- $\frac{\partial \det(A)}{\partial A} = \det(A) \cdot (A^{-1})^T$.
Esta fórmula é válida para matrizes invertíveis. Intuitivamente, a sensitividade do determinante a mudanças em $A$ depende do próprio determinante e da inversa de $A$.
Para uma matriz $2 \times 2$, $A = \begin{bmatrix} a & b \ c & d \end{bmatrix}$, temos fórmulas explícitas:
- $\frac{\partial \det(A)}{\partial a} = d$;
- $\frac{\partial \det(A)}{\partial b} = -c$;
- $\frac{\partial \det(A)}{\partial c} = -b$;
- $\frac{\partial \det(A)}{\partial d} = a$.
Exemplo Numérico: Para $A = \begin{bmatrix} 3 & 2 \ 1 & 5 \end{bmatrix}$, temos $\det(A) = 3 \times 5 - 2 \times 1 = 13$.
Aumentando $A_{11}$ por 0.1, o novo determinante será: $\det\begin{bmatrix} 3.1 & 2 \ 1 & 5 \end{bmatrix} = 3.1 \times 5 - 2 \times 1 = 15.5 - 2 = 13.5$
A mudança foi de 0.5, que corresponde a $\frac{\partial \det(A)}{\partial A_{11}} = A_{22} = 5$, como esperado.
-
Inversa de Matriz: a inversa de uma matriz é uma operação fundamental que transforma $A$ em $A^{-1}$ tal que $AA^{-1} = A^{-1}A = I$.
\[f(A) = A^{-1}\]Derivada: A derivada da inversa em relação aos elementos da matriz original envolve a própria inversa:
\[\frac{\partial (A^{-1})_{ij}}{\partial A_{kl}} = -(A^{-1})_{ik}(A^{-1})_{lj}\]Em notação matricial mais compacta:
\[\frac{\partial A^{-1}}{\partial A_{kl}} = -A^{-1} E_{kl} A^{-1}\]Na qual, $E_{kl}$ é uma matriz com 1 na posição $(k,l)$ e 0 nas demais.
Esta fórmula demonstra como pequenas mudanças em $A$ propagam não-linearmente para sua inversa, através de um “sanduíche” de multiplicações matriciais.
Exemplo Numérico: para $A = \begin{bmatrix} 2 & 1 \ 1 & 1 \end{bmatrix}$, a inversa é $A^{-1} = \begin{bmatrix} 1 & -1 \ -1 & 2 \end{bmatrix}$.
Se perturbarmos $A_{11}$ por $0.1$:
\[A = \begin{bmatrix} 2.1 & 1 \\ 1 & 1 \end{bmatrix}\]A nova inversa seria:
\[A^{-1} = \begin{bmatrix} 0.9091 & -0.9091 \\ -0.9091 & 1.9091 \end{bmatrix} \text{(arredondado para 4 casas decimais)}\]A mudança em $(A^{-1})_{11}$ é aproximadamente $-0.0909$, que está alinhada com a fórmula da derivada.
Propriedades Úteis e Identidades
Além das derivadas básicas acima, existem algumas identidades do cálculo com matrizes que serão úteis para o entendimento de operações diferenciáveis especialmente nos algoritmos que envolvem aprendizado profundo. Algumas delas incluem:
-
Regra da Cadeia para Funções Matriciais:
Se $f(X) = g(h(X))$, então $\nabla f(X) = \nabla h(X) \cdot \nabla g(h(X))$, onde o operador $\cdot$ representa a aplicação apropriada da regra da cadeia.
-
Derivada do Traço de um Produto:
\[\frac{\partial \text{tr}(AB)}{\partial A} = B^T\] \[\frac{\partial \text{tr}(AB)}{\partial B} = A^T\] -
Derivada do Traço de uma Transformação Quadrática:
\[\frac{\partial \text{tr}(AXB)}{\partial X} = A^T B^T\] -
Derivada do Traço de uma Forma Quadrática:
\[\frac{\partial \text{tr}(X^TAX)}{\partial X} = (A + A^T)X\]
Estas identidades são particularmente úteis em otimização, onde muitas funções de perda podem ser expressas em termos de traços.
Aplicações em Aprendizado Profundo e Transformers
As operações de matrizes diferenciáveis são o fundamento matemático do aprendizado profundo. Elas permitem:
- Retropropagação em Redes Neurais: a retropropagação (backpropagation) é um algoritmo que utiliza a regra da cadeia para calcular gradientes em redes neurais. As operações matriciais diferenciáveis permitem o fluxo suave de informação do gradiente através das camadas da rede. Considerando um modelo simples:
no qual $W$ é uma matriz de pesos, $b$ é um vetor de viés, $x$ é o vetor de entrada e $\sigma$ é uma função de ativação não-linear.
Para uma função de perda $L$, calculamos:
\[\frac{\partial L}{\partial W} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial Wx} \cdot \frac{\partial (Wx)}{\partial W}\]Cada uma dessas derivadas envolve operações matriciais diferenciáveis que permitem o ajuste gradual dos pesos em direção ao mínimo da função de perda.
- Otimização de Matrizes de Embedding: em processamento de linguagem natural, as palavras são frequentemente representadas como vetores de embedding. Estes embeddings são linhas, vetores, de uma matriz $E$ que é otimizada através de operações diferenciáveis. Por exemplo, no modelo word2vec, a probabilidade de uma palavra de saída $w_O$ dada uma palavra de entrada $w_I$ será calculada como:
neste caso, $v_{w_I}$ e $v_{w_O}$ são vetores de embedding para palavras de entrada e saída, respectivamente.
A otimização destes embeddings requer o cálculo de gradientes de operações como produtos escalares e multiplicações de matrizes.
- Mecanismos de Atenção nos Transformers: nos modelos Transformer, o mecanismo de atenção utiliza extensivamente operações matriciais diferenciáveis. A atenção é calculada como:
Na qual, $Q$, $K$, e $V$ são matrizes de consulta, chave e valor.
O cálculo dos gradientes para atualizar estas matrizes depende fundamentalmente das derivadas das operações de multiplicação matricial, transposição e outras operações diferenciáveis discutidas anteriormente.
Exemplo de Operações Matriciais Diferenciáveis em C++ 20
#include <iostream> ///< Para entrada e saída padrão (std::cout, std::cerr).
#include <vector> ///< Para contêiner std::vector usado em matrizes manuais.
#include <iomanip> ///< Para std::fixed e std::setprecision, usados na formatação de saída.
#include <stdexcept> ///< Para exceções padrão como std::invalid_argument.
#include <Eigen/Dense> ///< Para a biblioteca Eigen, usada em operações matriciais.
#include <cmath> ///< Para std::abs, usado em comparações de ponto flutuante.
/**
* @class DifferentiableMatrixOperations
* @brief Uma classe para demonstrar operações matriciais diferenciáveis e suas derivadas.
*
* Implementa operações como adição, multiplicação, traço, determinante e inversa de matrizes,
* com métodos para calcular derivadas aproximadas numericamente. Usa a biblioteca Eigen para
* operações eficientes e fornece exemplos numéricos para ilustrar a diferenciabilidade.
*/
class DifferentiableMatrixOperations {
private:
static constexpr double epsilon = 1e-6; ///< Pequena perturbação para cálculo numérico de derivadas.
/**
* @brief Imprime uma matriz Eigen com um nome opcional.
* @param matrix A matriz Eigen a ser impressa.
* @param name Nome opcional a ser exibido antes da matriz.
*/
template<typename Derived>
static void printMatrix(const Eigen::MatrixBase<Derived>& matrix, const std::string& name = "") {
if (!name.empty()) {
std::cout << name << " =\n";
}
std::cout << matrix << "\n";
}
public:
/**
* @brief Realiza a adição de duas matrizes e calcula derivadas parciais aproximadas.
* @param A Primeira matriz (Eigen::MatrixXd).
* @param B Segunda matriz (Eigen::MatrixXd).
* @return A matriz resultante da adição.
* @throws std::invalid_argument Se as dimensões forem incompatíveis.
*/
static Eigen::MatrixXd matrixAddition(const Eigen::MatrixXd& A, const Eigen::MatrixXd& B) {
if (A.rows() != B.rows() || A.cols() != B.cols()) {
throw std::invalid_argument("Dimensões incompatíveis para adição de matrizes");
}
return A + B;
}
/**
* @brief Demonstra a derivada da adição de matrizes (∂(A+B)/∂A = I, ∂(A+B)/∂B = I).
* @param A Matriz de entrada para perturbação.
* @param B Matriz fixa.
* @param i Índice da linha do elemento a perturbar.
* @param j Índice da coluna do elemento a perturbar.
* @return Matriz de derivadas aproximadas para ∂(A+B)/∂A(i,j).
*/
static Eigen::MatrixXd derivativeMatrixAddition(const Eigen::MatrixXd& A, const Eigen::MatrixXd& B, int i, int j) {
Eigen::MatrixXd A_perturbed = A;
A_perturbed(i, j) += epsilon;
Eigen::MatrixXd result = matrixAddition(A_perturbed, B);
Eigen::MatrixXd base = matrixAddition(A, B);
return (result - base) / epsilon; // Derivada numérica: [f(A+h) - f(A)] / h
}
/**
* @brief Realiza a multiplicação de duas matrizes.
* @param A Primeira matriz (Eigen::MatrixXd).
* @param B Segunda matriz (Eigen::MatrixXd).
* @return A matriz resultante da multiplicação.
* @throws std::invalid_argument Se as dimensões forem incompatíveis.
*/
static Eigen::MatrixXd matrixMultiplication(const Eigen::MatrixXd& A, const Eigen::MatrixXd& B) {
if (A.cols() != B.rows()) {
throw std::invalid_argument("Dimensões incompatíveis para multiplicação de matrizes");
}
return A * B;
}
/**
* @brief Demonstra a derivada da multiplicação de matrizes (∂(AB)/∂A, ∂(AB)/∂B).
* @param A Matriz de entrada para perturbação.
* @param B Matriz fixa.
* @param i Índice da linha do elemento a perturbar.
* @param j Índice da coluna do elemento a perturbar.
* @param with_respect_to Indica se a derivada é em relação a A ("A") ou B ("B").
* @return Matriz de derivadas aproximadas.
*/
static Eigen::MatrixXd derivativeMatrixMultiplication(const Eigen::MatrixXd& A, const Eigen::MatrixXd& B,
int i, int j, const std::string& with_respect_to) {
if (with_respect_to == "A") {
Eigen::MatrixXd A_perturbed = A;
A_perturbed(i, j) += epsilon;
Eigen::MatrixXd result = matrixMultiplication(A_perturbed, B);
Eigen::MatrixXd base = matrixMultiplication(A, B);
return (result - base) / epsilon;
} else if (with_respect_to == "B") {
Eigen::MatrixXd B_perturbed = B;
B_perturbed(i, j) += epsilon;
Eigen::MatrixXd result = matrixMultiplication(A, B_perturbed);
Eigen::MatrixXd base = matrixMultiplication(A, B);
return (result - base) / epsilon;
}
throw std::invalid_argument("Parâmetro 'with_respect_to' deve ser 'A' ou 'B'");
}
/**
* @brief Calcula o traço de uma matriz quadrada.
* @param A Matriz quadrada (Eigen::MatrixXd).
* @return O valor escalar do traço.
* @throws std::invalid_argument Se a matriz não for quadrada.
*/
static double matrixTrace(const Eigen::MatrixXd& A) {
if (A.rows() != A.cols()) {
throw std::invalid_argument("Matriz deve ser quadrada para cálculo do traço");
}
return A.trace();
}
/**
* @brief Demonstra a derivada do traço (∂tr(A)/∂A = I).
* @param A Matriz de entrada para perturbação.
* @param i Índice da linha do elemento a perturbar.
* @param j Índice da coluna do elemento a perturbar.
* @return Derivada aproximada do traço em relação a A(i,j).
*/
static double derivativeMatrixTrace(const Eigen::MatrixXd& A, int i, int j) {
Eigen::MatrixXd A_perturbed = A;
A_perturbed(i, j) += epsilon;
double result = matrixTrace(A_perturbed);
double base = matrixTrace(A);
return (result - base) / epsilon;
}
/**
* @brief Calcula o determinante de uma matriz quadrada.
* @param A Matriz quadrada (Eigen::MatrixXd).
* @return O valor escalar do determinante.
* @throws std::invalid_argument Se a matriz não for quadrada.
*/
static double matrixDeterminant(const Eigen::MatrixXd& A) {
if (A.rows() != A.cols()) {
throw std::invalid_argument("Matriz deve ser quadrada para cálculo do determinante");
}
return A.determinant();
}
/**
* @brief Demonstra a derivada do determinante (∂det(A)/∂A = det(A) * (A^-1)^T).
* @param A Matriz de entrada para perturbação.
* @param i Índice da linha do elemento a perturbar.
* @param j Índice da coluna do elemento a perturbar.
* @return Derivada aproximada do determinante em relação a A(i,j).
*/
static double derivativeMatrixDeterminant(const Eigen::MatrixXd& A, int i, int j) {
Eigen::MatrixXd A_perturbed = A;
A_perturbed(i, j) += epsilon;
double result = matrixDeterminant(A_perturbed);
double base = matrixDeterminant(A);
return (result - base) / epsilon;
}
/**
* @brief Calcula a inversa de uma matriz quadrada.
* @param A Matriz quadrada (Eigen::MatrixXd).
* @return A matriz inversa.
* @throws std::invalid_argument Se a matriz não for quadrada ou não for invertível.
*/
static Eigen::MatrixXd matrixInverse(const Eigen::MatrixXd& A) {
if (A.rows() != A.cols()) {
throw std::invalid_argument("Matriz deve ser quadrada para cálculo da inversa");
}
if (std::abs(A.determinant()) < 1e-9) {
throw std::invalid_argument("Matriz não é invertível (determinante próximo de zero)");
}
return A.inverse();
}
/**
* @brief Demonstra a derivada da inversa (∂(A^-1)/∂A).
* @param A Matriz de entrada para perturbação.
* @param i Índice da linha do elemento a perturbar.
* @param j Índice da coluna do elemento a perturbar.
* @return Matriz de derivadas aproximadas para ∂(A^-1)/∂A(i,j).
*/
static Eigen::MatrixXd derivativeMatrixInverse(const Eigen::MatrixXd& A, int i, int j) {
Eigen::MatrixXd A_perturbed = A;
A_perturbed(i, j) += epsilon;
Eigen::MatrixXd result = matrixInverse(A_perturbed);
Eigen::MatrixXd base = matrixInverse(A);
return (result - base) / epsilon;
}
};
/**
* @brief Função principal que demonstra operações matriciais diferenciáveis.
*
* Este programa implementa exemplos numéricos para adição, multiplicação, traço, determinante e inversa
* de matrizes, calculando derivadas aproximadas numericamente. Inclui os exemplos do documento e um caso
* simples de retropropagação para ilustrar a aplicação em aprendizado profundo.
*
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
std::cout << std::fixed << std::setprecision(2);
std::cout << "Demonstração de Operações Matriciais Diferenciáveis\n";
std::cout << "--------------------------------------------------\n\n";
// Exemplo 1: Adição de matrizes
std::cout << "Exemplo 1: Adição de Matrizes e Derivada\n";
Eigen::Matrix2d A1;
A1 << 1.0, 2.0,
3.0, 4.0;
Eigen::Matrix2d B1;
B1 << 5.0, 6.0,
7.0, 8.0;
try {
DifferentiableMatrixOperations::printMatrix(A1, "Matriz A");
DifferentiableMatrixOperations::printMatrix(B1, "Matriz B");
Eigen::MatrixXd sum = DifferentiableMatrixOperations::matrixAddition(A1, B1);
DifferentiableMatrixOperations::printMatrix(sum, "A + B");
// Derivada em relação a A(0,0)
Eigen::MatrixXd deriv_add = DifferentiableMatrixOperations::derivativeMatrixAddition(A1, B1, 0, 0);
DifferentiableMatrixOperations::printMatrix(deriv_add, "∂(A+B)/∂A(0,0)");
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
// Exemplo 2: Multiplicação de matrizes
std::cout << "\nExemplo 2: Multiplicação de Matrizes e Derivada\n";
Eigen::Matrix2d A2;
A2 << 2.0, 3.0,
4.0, 1.0;
Eigen::Matrix2d B2;
B2 << 1.0, 5.0,
2.0, 3.0;
try {
DifferentiableMatrixOperations::printMatrix(A2, "Matriz A");
DifferentiableMatrixOperations::printMatrix(B2, "Matriz B");
Eigen::MatrixXd prod = DifferentiableMatrixOperations::matrixMultiplication(A2, B2);
DifferentiableMatrixOperations::printMatrix(prod, "A * B");
// Derivada em relação a A(1,2)
Eigen::MatrixXd deriv_mult_A = DifferentiableMatrixOperations::derivativeMatrixMultiplication(A2, B2, 0, 1, "A");
DifferentiableMatrixOperations::printMatrix(deriv_mult_A, "∂(A*B)/∂A(0,1)");
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
// Exemplo 3: Traço de matriz
std::cout << "\nExemplo 3: Traço de Matriz e Derivada\n";
Eigen::Matrix2d A3;
A3 << 3.0, 2.0,
1.0, 5.0;
try {
DifferentiableMatrixOperations::printMatrix(A3, "Matriz A");
double trace = DifferentiableMatrixOperations::matrixTrace(A3);
std::cout << "tr(A) = " << trace << "\n";
// Derivada em relação a A(0,0)
double deriv_trace = DifferentiableMatrixOperations::derivativeMatrixTrace(A3, 0, 0);
std::cout << "∂tr(A)/∂A(0,0) = " << deriv_trace << " (esperado: 1.0)\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
// Exemplo 4: Determinante de matriz
std::cout << "\nExemplo 4: Determinante de Matriz e Derivada\n";
Eigen::Matrix2d A4;
A4 << 3.0, 2.0,
1.0, 5.0;
try {
DifferentiableMatrixOperations::printMatrix(A4, "Matriz A");
double det = DifferentiableMatrixOperations::matrixDeterminant(A4);
std::cout << "det(A) = " << det << "\n";
// Derivada em relação a A(0,0)
double deriv_det = DifferentiableMatrixOperations::derivativeMatrixDeterminant(A4, 0, 0);
std::cout << "∂det(A)/∂A(0,0) = " << deriv_det << " (esperado: A(1,1) = 5.0)\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
// Exemplo 5: Inversa de matriz
std::cout << "\nExemplo 5: Inversa de Matriz e Derivada\n";
Eigen::Matrix2d A5;
A5 << 2.0, 1.0,
1.0, 1.0;
try {
DifferentiableMatrixOperations::printMatrix(A5, "Matriz A");
Eigen::MatrixXd inv = DifferentiableMatrixOperations::matrixInverse(A5);
DifferentiableMatrixOperations::printMatrix(inv, "A^-1");
// Derivada em relação a A(0,0)
Eigen::MatrixXd deriv_inv = DifferentiableMatrixOperations::derivativeMatrixInverse(A5, 0, 0);
DifferentiableMatrixOperations::printMatrix(deriv_inv, "∂(A^-1)/∂A(0,0)");
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
// Exemplo 6: Retropropagação simples
std::cout << "\nExemplo 6: Retropropagação Simples\n";
Eigen::MatrixXd W(2, 2); // Matriz de pesos
W << 1.0, 0.5,
0.3, 1.2;
Eigen::VectorXd x(2); // Vetor de entrada
x << 0.4, 0.6;
Eigen::VectorXd y_true(2); // Saída desejada
y_true << 1.0, 0.0;
try {
DifferentiableMatrixOperations::printMatrix(W, "Matriz de pesos W");
DifferentiableMatrixOperations::printMatrix(x, "Vetor de entrada x");
DifferentiableMatrixOperations::printMatrix(y_true, "Saída desejada y_true");
// Forward pass: y = W * x
Eigen::VectorXd y_pred = W * x;
DifferentiableMatrixOperations::printMatrix(y_pred, "Saída predita y_pred");
// Função de perda: L = ||y_true - y_pred||^2
Eigen::VectorXd error = y_true - y_pred;
double loss = error.squaredNorm();
std::cout << "Perda L = " << loss << "\n";
// Gradiente da perda em relação a y_pred: ∂L/∂y_pred = -2 * (y_true - y_pred)
Eigen::VectorXd dL_dy_pred = -2.0 * error;
DifferentiableMatrixOperations::printMatrix(dL_dy_pred, "∂L/∂y_pred");
// Gradiente da perda em relação a W: ∂L/∂W = (∂L/∂y_pred) * x^T
Eigen::MatrixXd dL_dW = dL_dy_pred * x.transpose();
DifferentiableMatrixOperations::printMatrix(dL_dW, "∂L/∂W");
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
return 0;
}
Transformações Afins: Um Pilar Matemático para Word Embeddings, Transformers e LLMs
Transformações afins são operações matemáticas essenciais em aprendizado de máquina, especialmente em processamento de linguagem natural (NLP). Notadamente em modelos como transformers, word embeddings e grandes modelos de linguagem (LLMs), permitindo a manipulação de vetores e matrizes de maneira a preservar propriedades geométricas como colinearidade e razões de distâncias.
Uma transformação afim é uma função que combina uma transformação linear com uma translação. Uma translação é uma operação geométrica que desloca cada ponto de um espaço por uma mesma distância em uma direção específica, preservando distâncias e ângulos entre pontos. Essencialmente, uma translação é um deslocamento rígido de um objeto sem rotação ou distorção. Formalmente, dada uma matriz $A$, que representa a transformação linear, e um vetor $b$, que representa a translação, a transformação afim $T$ de um vetor $x$ será definida como:
\[T(x) = A x + b\]De forma que:
- $x \in \mathbb{R}^n$ é o vetor de entrada;
- $A \in \mathbb{R}^{m \times n}$ é a matriz de transformação linear;
- $b \in \mathbb{R}^m$ é o vetor de translação;
- $T(x) \in \mathbb{R}^m$ é o vetor resultante.
Essa operação pode incluir rotações, escalonamentos, cisalhamentos e deslocamentos, dependendo das propriedades de $A$ e $b$. Em Processamento de Linguagem Natural, essas transformações são aplicadas a vetores de alta dimensão que representam palavras, tokens ou sequências.
| Contexto | Aplicações de Transformações Afins |
|---|---|
| Word Embeddings | Captura de Relações Semânticas: Transformações lineares mapeiam relações entre palavras (ex: $v_{\text{rainha}} \approx A v_{\text{rei}}$) Normalização e Centralização: Translação $b$ centraliza embeddings; matriz $A$ escala vetores Redução de Dimensionalidade: Técnicas como PCA aplicam transformações lineares para projetar embeddings em espaços menores |
| Transformers | Mecanismo de Atenção: Matrizes de consulta, chave e valor são geradas por transformações lineares ($Q = W_Q x$, etc.) Camadas Feed-Forward: Cada bloco inclui transformação afim com não-linearidade: $\text{FFN}(x) = \sigma(W_1 x + b_1) W_2 + b_2$ Normalização de Camada: Layer normalization ajusta ativações: $y = \gamma \cdot \frac{x - \mu}{\sigma} + \beta$ |
| LLMs | Embeddings de Entrada e Saída: Tokens mapeados para vetores via matriz de embedding; saídas projetadas de volta ao vocabulário Atenção Multi-Cabeça: Cada cabeça aplica transformações lineares independentes, resultados combinados Adaptação a Tarefas: Durante fine-tuning, camadas superiores aplicam transformações afins para tarefas específicas |
Tabela 1: A relevância das transformações afins em Processamento de Linguagem Natural destacando word embedding, transformers e LLMs_
Propriedades Importantes
As transformações afins possuem características que as tornam ideais para word embeddings e transformers:
- Preservação de Colinearidade: pontos alinhados permanecem alinhados após a transformação;
- Preservação de Razões de Distâncias: a proporção entre distâncias em uma linha é mantida;
- Composição: a combinação de duas transformações afins resulta em outra transformação afim;
- Inversibilidade: Se $A$ é invertível, $T(x)$ pode ser revertida: $x = A^{-1} (T(x) - b)$.
Exemplo Numérico
Considere um vetor $x = \begin{bmatrix} 1 \ 2 \end{bmatrix}$, uma matriz $A = \begin{bmatrix} 2 & 1 \ 0 & 3 \end{bmatrix}$ e um vetor $b = \begin{bmatrix} 3 \ 1 \end{bmatrix}$. A transformação afim é:
\[T(x) = A x + b = \begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix} + \begin{bmatrix} 3 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \cdot 1 + 1 \cdot 2 \\ 0 \cdot 1 + 3 \cdot 2 \end{bmatrix} + \begin{bmatrix} 3 \\ 1 \end{bmatrix} = \begin{bmatrix} 4 \\ 6 \end{bmatrix} + \begin{bmatrix} 3 \\ 1 \end{bmatrix} = \begin{bmatrix} 7 \\ 7 \end{bmatrix}\]Esse exemplo ilustra como $A$ aplica uma transformação linear (escalamento e cisalhamento) e $b$ desloca o resultado.
Implementação em C++ 20
Abaixo, apresentamos uma implementação em C++ 20 usando a biblioteca Eigen para aplicar transformações afins, seguindo o estilo do documento fornecido.
#include <iostream>
#include <Eigen/Dense>
#include <iomanip> ///< Adicionando esta biblioteca para std::setprecision
#include <stdexcept>
/**
* @brief Aplica uma transformação afim a um vetor.
* @param A Matriz de transformação linear.
* @param b Vetor de translação.
* @param x Vetor de entrada.
* @return O vetor transformado T(x) = Ax + b.
* @throws std::invalid_argument Se as dimensões forem incompatíveis.
*/
Eigen::VectorXd affineTransform(const Eigen::MatrixXd& A, const Eigen::VectorXd& b, const Eigen::VectorXd& x) {
if (A.cols() != x.size() || A.rows() != b.size()) {
throw std::invalid_argument("Dimensões incompatíveis para transformação afim");
}
return A * x + b;
}
/**
* @brief Função principal que demonstra a aplicação de uma transformação afim.
* @return 0 em caso de execução bem-sucedida.
*/
int main() {
std::cout << std::fixed << std::setprecision(2);
std::cout << "Demonstração de Transformação Afim\n";
std::cout << "---------------------------------\n\n";
// Definição da matriz A, vetor b e vetor x
Eigen::MatrixXd A(2, 2);
A << 2.0, 1.0,
0.0, 3.0;
Eigen::Vector2d b(3.0, 1.0);
Eigen::Vector2d x(1.0, 2.0);
std::cout << "Matriz A =\n" << A << "\n\n";
std::cout << "Vetor b =\n" << b << "\n\n";
std::cout << "Vetor x =\n" << x << "\n\n";
try {
Eigen::VectorXd result = affineTransform(A, b, x);
std::cout << "T(x) = Ax + b =\n" << result << "\n";
} catch (const std::exception& e) {
std::cerr << "Erro: " << e.what() << "\n";
}
return 0;
}
-
VASWANI, Ashish et al. Attention is all you need. In: ADVANCES IN NEURAL INFORMATION PROCESSING SYSTEMS, 30., 2017, Long Beach. Proceedings of the […]. Red Hook: Curran Associates, Inc., 2017. p. 5998-6008. Disponível em: https://papers.nips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf. Acesso em: 09 fevereiro 2024. ↩