A esforçada leitora, se realmente quiser entender as técnicas e algoritmos de Reinforcement Learning - RL, deve começar com problemas simples. Não é qualquer problema. Problemas que permitam construir uma compreensão sólida dos princípios estruturantes desta tecnologia. É aqui que o Grid World brilha e se destaca.

A simplicidade do Grid World reside em não ser um desafio do mundo real, como dirigir um carro, ou jogar um jogo de estratégia. Em vez disso, este problema usa um mundo representado por um ambiente formado por uma grade bidimensional, discreta e simplificada. Um mundo cuidadosamente projetado para isolar e destacar os conceitos mais importantes do RL. Não é raro que a simplicidade deste problema faça com que ele seja escolhido para testar novos algoritmos, novas ideias.

Historicamente, o Grid World e problemas similares, foram utilizados para o desenvolvimento e validação dos primeiros algoritmos de RL, como Q-Learning e SARSA. Além disso, este é um problema de decisão sequencial.

A ênfase na natureza sequencial dos Processos de Decisão de Markov não é por acaso. Esta característica distingue os MDPs de outros modelos de decisão e reflete mais fielmente a realidade dos problemas que encontramos tanto na natureza quanto em sistemas artificiais.

A atenta leitora pode, simplesmente, imaginar um jogador de xadrez. Cada movimento que ele faz não pode ser considerado isoladamente. A posição de uma peça determinará não apenas o resultado imediato, mas também moldará todas as possibilidades de jogadas futuras. Esta é a essência de um problema de decisão sequencial, no qual cada escolha se entrelaça com um futuro estocástico.

Em contraste com problemas de decisão única, domínio da programação linear, em que podemos simplesmente otimizar uma determinada solução em busca de um resultado imediato, os problemas sequenciais exigem uma compreensão profunda das relações temporais. Uma decisão aparentemente subótima em um determinado momento pode ser parte de uma estratégia superior se observada ao longo do tempo. Este conceito permite que a esforçada leitora possa entender por que os MDPs são tão poderosos na modelagem de problemas do mundo real.

A dependência temporal em problemas sequenciais cria uma teia complexa de causa e efeito. Cada ação não apenas gera uma recompensa imediata, mas também transporta o sistema para um novo estado, que por sua vez determina quais ações estarão disponíveis no futuro e quais recompensas serão possíveis. Esta cadeia de influências torna o planejamento em MDPs um desafio particularmente interessante. Neste cenário, o trabalho de Markov permite estabelecer que o estado atual contém toda a informação necessária para tomar decisões ótimas, permitindo navegar pela complexidade dos problemas sequenciais sem nos perdermos no labirinto do passado.

A criativa leitora deve imaginar cada estado como sendo uma fotografia completa do sistema, capturando tudo que precisamos saber para seguir adiante. Esta característica sequencial também distingue os MDPsde outros paradigmas de aprendizado de máquina.

Enquanto problemas de classificação ou regressão lidam com mapeamentos estáticos de entradas para saídas, os MDPs forçam a consideração das consequências de longo prazo das decisões tomadas. Introduzindo questões sobre o equilíbrio entre exploração e explotação, sobre como aprender com experiências passadas e sobre como planejar para um futuro incerto.

Exploração (exploration) refere-se a buscar e descobrir novas possibilidades/ações enquanto explotação (exploitation) refere-se a utilizar o conhecimento já adquirido para maximizar recompensas.

Em essência, a natureza sequencial dos MDPsnão é apenas uma característica técnica do modelo. Trata-se de um reflexo de como decisões se desdobram no tempo real. Cada escolha é um elo em uma cadeia contínua de causa e efeito. Esta compreensão permite que qualquer um que busque aplicar MDPsa problemas práticos ou teóricos.

All models are wrong, but some are useful. George Box.

O MDP permite a criação de modelos, apenas modelos. Nada mais, nada menos. Dessa forma, existe uma imperfeição inerente aos processos estocásticos envolvidos. Antes de continuarmos, podemos concordar com algumas definições que serão úteis ao longo do processo de estudo.

1. Agente: no contexto do MDP um agente é a entidade que interage com o ambiente e toma decisões. O agente é o componente que observa o estado atual do ambiente, escolhe ações com base em sua política (strategy/policy) e recebe recompensas como resultado dessas ações. A esforçada leitora pode pensar no agente como um tomador de decisões que está constantemente aprendendo e se adaptando para maximizar suas recompensas ao longo do tempo.

   Uma “política” (policy em inglês) é simplesmente um mapeamento que diz qual ação tomar em cada estado possível do ambiente. É como um conjunto de regras de decisão - para cada situação que você encontra, a política te diz o que fazer.

   A “política ótima” seria o conjunto de decisões que leva às melhores recompensas possíveis.

2. Estados: um estado em um MDP é uma fotografia completa do sistema em um dado momento. Como se a sagaz leitora pudesse pausar o tempo e capturar toda informação necessária a tomada de decisão. A característica fundamental de um estado em um MDP é que ele possui a propriedade de Markov. Isso significa que o estado atual contém toda a informação necessária para decidir a próxima ação, sem precisar de informações anteriores. Por exemplo: em um jogo de xadrez, o estado seria a posição atual de todas as peças no tabuleiro. Não importa qual sequência de movimentos montou o tabuleiro. Apenas a configuração atual será relevante na previsão do acontecerá a seguir.

3. Ações: as ações são as diferentes escolhas disponíveis ao agente em cada estado. A perspicaz leitora deve entender que as ações são os únicos elementos que o agente pode controlar. Em um MDP, em cada estado, existe um conjunto de ações possíveis, denominado $A(s)$, no qual $s$ é o estado atual. Ainda no xadrez, as ações seriam os movimentos legais possíveis para as peças na posição atual. Se você tem um cavalo em $b1$, uma ação possível seria movê-lo para $c3$.

4. Recompensas: as recompensas são como sinais numéricos que guiam o agente em direção ao comportamento desejado. A função de recompensa $R(s,a,s’)$ mapeia cada par estado-ação para um valor numérico. Este valor representa o quão bom foi tomar aquela ação naquele estado. A recompensa é imediata e não considera consequências futuras da ação. Voltando ao exemplo do xadrez, capturar uma rainha poderia dar uma recompensa alta imediata $(+9)$, mesmo que isso possa levar a uma posição tática desfavorável no futuro.

5. Dinâmica: a dinâmica do sistema, também chamada de função de transição $P(s’ \vert s,a)$, descreve como o mundo evolui em resposta às ações do agente. Esta função determina a probabilidade de alcançar um estado $s’$ quando tomamos a ação a no estado $s$. A propriedade mais importante da dinâmica em um MDP é que ela depende apenas do estado atual e da ação escolhida.

6. Planejamento: no planejamento, assume-se que todos os componentes são conhecidos. O objetivo do agente, tomador de decisão, é encontrar uma política, isto é, um mapeamento do histórico de observações de estados para ações, que maximize alguma função objetivo da recompensa.

Um Pouco de Sanidade Não Faz Mal a Ninguém

Até este momento, utilizamos a notação tradicional da teoria da probabilidade, com $X_n$ representando estados e

\[P_{ij}\]

ou

\[P(X_{n+1} = j\vert X_n = i)\]

representando probabilidades de transição. Esta notação serviu bem ao propósito de estabelecer as bases matemáticas dos processos estocásticos e das Cadeias de Markov. No entanto, ao entrarmos no domínio do Reinforcement Learning - RL, adotaremos a notação padrão desta área.

Em RL, representamos estados como $s$ e $s’$, ao invés de $X_n$ e $X_{n+1}$. Esta mudança não é apenas uma preferência estética, reflete uma sutileza importante: em RL, frequentemente estamos mais preocupados com a relação entre estados e menos preocupados com sua evolução temporal explícita. A notação $s$ e $s’$ enfatiza a transição de um estado para outro, independentemente do momento específico em que isso ocorre.

As probabilidades de transição também ganham um novo elemento: a ação $a$. Assim, $P(s’\vert s,a)$ substitui nossa notação anterior $P(X_{n+1} = j\vert X_n = i)$. Esta mudança destaca o papel central do agente no processo de decisão. Não estamos mais apenas observando transições, mas ativamente influenciando-as através de ações.

Esta nova notação permite expressar conceitos de RL de forma natural e intuitiva. Por exemplo: uma política $\pi(s)$ mapeia estados para ações, e a função valor $V^\pi(s)$ representa o valor esperado de longo prazo de estar em um estado $s$ seguindo a política $\pi$. Estas ideias, embora possíveis de expressar na notação anterior, tornam-se mais claras e diretas com a notação padrão de RL.

Deste ponto em diante, adotaremos esta notação padrão de RL. Entretanto, é importante que a atenta leitora mantenha em mente que esta notação representa os mesmos conceitos que desenvolvemos anteriormente, apenas expressos de uma forma mais adequada ao estudo de Reinforcement Learning.

Grid World: Um Problema de Processo de Decisão de Markov (MDP)

No coração do Grid World reside o conceito de Processo de Decisão de Markov - MDP. Um MDP fornece uma estrutura matemática formal para modelar tomadas de decisão sequenciais em ambientes estocásticos¹, nos quais o resultado de uma ação é probabilístico. Em termos mais simples, dizemos que o Grid World é, portanto, um exemplo prático e intuitivo de um MDP.

Imagine um tabuleiro retangular, como um tabuleiro de xadrez simplificado. Sem as casas de cores diferentes. Este é o nosso Grid World. Cujo exemplo, pode ser visto na Figura 1.

Figura 1: Exemplo de Grid World mostrando um agente, recompensa e punição².

Antes de prosseguirmos pode ser produtivo detalhar os componentes deste mundo:

1. Células como Estados: cada célula dentro da grade representa um estado distinto no qual o agente pode se encontrar. A posição do agente na grade define completamente o estado do ambiente.

2. Paredes como Limitações: algumas células podem ser designadas como paredes, atuando como obstáculos intransponíveis. Paredes restringem o movimento do agente, adicionando um elemento de desafio e realismo ao ambiente.

3. Movimento Estocástico: quando o agente decide se mover (por exemplo: para o norte), o resultado não será determinístico. Introduzimos características estocásticas ao movimento:

• Em $80\%$ das vezes, o agente se move na direção desejada.

• Em $10\%$ das vezes, o agente se move para cada lado perpendicular à direção desejada. Por exemplo: se tentar ir para o norte, pode ir para o leste ou oeste com $10\%$ de probabilidade cada. Como pode ser visto na Figura 2.

Figura 2: Visualização do efeito estocástico do movimento.

Se a ação resultante levar o agente a colidir com uma parede, o agente permanece no estado atual. Essa regra garante que o agente não possa atravessar paredes.

Esta característica estocástica no movimento força o agente a lidar com a incerteza e planejar suas ações considerando as possíveis consequências não determinísticas.

Sistema de Recompensas: Incentivando o Comportamento Desejado

Para que o agente aprenda a navegar no Grid World de forma inteligente, vamos criar e fornecer um sistema de recompensas que guie seu aprendizado. Para tanto, vamos definir o nosso sistema de recompensas segundo as seguintes regras:

1. Recompensa por vida ou passo: A cada passo que o agente dá na grade, exceto nos estados terminais, ele recebe uma pequena recompensa, também chamada de recompensa passo (em inglês, living reward). Essa recompensa pode ser positiva ou negativa:

• uma recompensa por passo negativa, como no exemplo fornecido, $-0.03$ incentiva o agente a alcançar os estados terminais o mais rápido possível, viver no ambiente tem um custo;

• uma recompensa por passo positiva, incentiva o agente a permanecer no ambiente o máximo possível, viver no ambiente sua recompensa, se não houvesse estados terminais atrativos;

• recompensas nos Estados Terminais: certos estados na grade são designados como estados terminais. Ao alcançar um estado terminal, o episódio de aprendizado se encerra, e o agente recebe uma grande recompensa, que pode ser: (a) positiva: representando um objetivo bem-sucedido, como alcançar um estado de meta ou coletar um recurso valioso (+1 na Figura 1); (b) negativa: Representando um resultado indesejado, como cair em um estado de armadilha ou falhar na tarefa (-1 na Figura 1).

O sistema de recompensas define o objetivo do agente no Grid World. O agente deve aprender a sequenciar suas ações de forma a maximizar a recompensa acumulada ao longo do tempo, considerando tanto as recompensas imediatas (recompensa por passo) quanto as recompensas futuras (recompensas nos estados terminais).

Estrutura Formal do MDP no Grid World

Agora, que a analítica leitora entendeu os conceitos, podemos mapear os componentes do Grid World na estrutura formal de um MDP:

1. Estados ($S$): o conjunto de todos os possíveis estados é representado por todas as células da grade. Na Figura 1, nosso mundo tem $12$ estados possíveis.

2. Ações ($A$): o conjunto de ações possíveis para o agente em cada estado consiste nos movimentos direcionais: ${Norte, Sul, Leste, Oeste}$.

3. Função de Transição ($P$): a função de transição $P(s′\vert s,a)$ define a probabilidade de, estando no estado $s$ e executando a ação $a$, o agente transite para o estado $s’$. No nosso Grid World, essa função é determinada pelas regras de movimento estocástico que definimos anteriormente ($80\%$ na direção desejada, $10\%$ para os lados, permanecer no mesmo estado se colidir com a parede).

4. Função de Recompensa ($R$): a função de recompensa $R(s,a,s′)$ define a recompensa que o agente recebe ao transitar do estado $s$ para o estado $s′$ após executar a ação $a$. No Grid World, isso engloba tanto as recompensas de passo, positivas e negativas, quanto as recompensas nos estados terminais.

5. Estado Inicial $(s_0)$: um estado específico na grade é designado como o estado inicial, Neste estado o agente começa cada episódio de aprendizado.

6. Estados Terminais ($S_terminal$):: um ou mais estados são designados como estados terminais. Ao alcançar um estado terminal, o episódio se encerra.

O Grid World, como um MDP, assume a propriedade de Markov. Essa propriedade simplifica o problema de aprendizado e tomada de decisão. Ela afirma que o futuro depende apenas do estado presente, e não do histórico passado de estados e ações.

Em termos práticos no Grid World, isso significa que a probabilidade de o agente se mover para um próximo estado e a recompensa que ele receberá dependem apenas da célula em que ele se encontra e da ação que ele escolher executar. O caminho que o agente percorreu para chegar ao estado atual e seu histórico de recompensas são irrelevantes para prever o futuro. Esta simplicidade sustenta o desenvolvimento de algoritmos eficientes de Reinforcement Learning.

A propriedade de Markov permite que os algoritmos de RL tomem decisões baseadas no estado atual, sem a necessidade de manter um histórico complexo de toda a trajetória do agente.

Grid World: Definição em Lógica de Primeira Ordem

Embora a formulação de MDP seja amplamente utilizada e eficaz para modelar o Grid World, podemos também descrever este ambiente de forma mais formal e rigorosa utilizando a Lógica de Primeira Ordem - FOL.

Essa abordagem não é comum e, talvez seja inédita. Então, se não for afeito às aventuras. Pule essa seção. Eu vou arriscar esta definição porque tenho ambições maiores que simplesmente entender RL e, enquanto explico um, vou criando bases de pesquisa. Mas, as vozes na minha cabeça, e o DuckduckGo dizem que não estou só ³, ⁴, ⁵.

A FOL permite definir o domínio do problema, as ações possíveis e o modelo de transição de forma declarativa e precisa. Esta abordagem pode ser particularmente útil para raciocínio formal sobre o ambiente e para conectar o RL com outras áreas da inteligência artificial, como o Planejamento Automatizado e os processos de racionalização.

Definição do Domínio

A definição de um mundo, Em FOL, começa pela definição dos termos primitivos e axiomas que descrevem este mundo. Neste caso, para Grid World, podemos começar por:

1. Termos Primitivos: definimos os seguintes predicados para descrever os elementos básicos do Grid World:

   • $\text{Celula}(x,y)$: este predicado é verdadeiro se a posição $(x,y)$ representa uma célula válida na grade;
   • $\text{Agente(x,y,t)}$: este predicado, é verdadeiro se o agente está localizado na célula $(x,y)$ no instante de tempo $t$.
   • $\text{Estado}(x,y,tipo)$: define o tipo de célula na posição $(x,y)$. O tipo pode ser $\text{vazio}$, $\text{parede}$, $\text{inicio}$, $\text{terminal}^+$ (terminal positivo) ou $\text{terminal}^-$ (terminal negativo).

2. Axiomas Básicos: estabelecemos agora alguns axiomas que restringem e definem o domínio do Grid World:

   • Axioma 1: tipo de célula Único: para cada célula $(x,y)$, existe um e apenas um tipo associado a ela. Formalmente, teremos:

     \[\forall x,y \exists! tipo \text{Estado}(x,y,tipo) \land tipo \in \\text{vazio, parede, inicio, terminal}^+, \text{terminal}^-\}\]

     Este axioma garante que cada célula tem um tipo bem definido e que esse tipo pertence ao conjunto de tipos possíveis.

   • Axioma 2: posição única do agente: em qualquer instante de tempo $t$, o agente pode estar em uma e apenas uma posição. Ou seja, teremos:

     \[\forall t \exists! x,y \;\text{Agente}(x,y,t)\]

     Este axioma assegura que o agente não pode estar em múltiplas posições simultaneamente.

Um mundo, qualquer mundo, que define um problema específico precisa da definição das ações que, por ventura, podem ser implementadas neste mundo. Em FOL, também podemos formalizar predicados referentes às ações que o agente pode executar no Grid World.

1. Ações Primitivas: definimos o conjunto de ações $A$ utilizando um predicado $Acao(a)$ que, pode ser definido como:

   \[\text{Acao}(a) \leftrightarrow a \in \{\text{Norte, Sul, Leste, Oeste}\}\]

   Este predicado define que as ações primitivas disponíveis para o agente são mover-se para $\text{Norte}$, $\text{Sul}$, $\text{Leste}$ ou $\text{Oeste}$.

2. Axiomas de Ação: introduzimos o predicado $\text{Executavel}(a,x,y)$ para definir quando uma ação a é executável a partir da célula $(x,y)$:

   \[\text{Executavel}(a,x,y) \leftrightarrow \exists x',y' \;[\text{Adjacente}(x,y,x',y',a) \land \neg \text{Estado}(x',y',\text{parede})]\]

   Na qual $\text{Adjacente}(x,y,x’,y’,a)$ é um predicado definido para ser verdadeiro se $(x’,y’)$ é adjacente a $(x,y)$ na direção da ação $a$. Este axioma estabelece que uma ação é executável se, na direção pretendida, não houver uma parede na célula adjacente.

3. Modelo de Transição: podemos definir um modelo de transição em FOL tanto para o caso determinístico quanto para o caso estocástico.

   • Caso Determinístico: se uma ação a é executável no estado $(x,y)$ no tempo $t$, então existe um único estado sucessor $(x’,y’)$ no tempo $t+1$:

     \[\forall x,y,t,a \; [\text{Agente}(x,y,t) \land \text{Executavel}(a,x,y)] \rightarrow\] \[\exists! x',y' \; [\text{Adjacente}(x,y,x',y',a) \land \text{Agente}(x',y',t+1)]\]

     Este axioma descreve a transição de estado para o caso em que o movimento é sempre bem-sucedido na direção desejada, caso a ação seja executável.

   • Caso Estocástico: para modelar o caso estocástico, como no nosso Grid World original, precisamos usar probabilidades. Por exemplo: para a ação $Norte$, podemos definir as probabilidades de transição da seguinte forma:

     • Probabilidade de mover para $\text{Norte}$ (direção desejada): $0.8$;

     • Probabilidade de mover para $\text{Leste}$ (perpendicular): $0.1$;

     • Probabilidade de mover para $\text{Oeste}$ (perpendicular): $0.1$.

     Estas transições podem ser representadas probabilisticamente em FOL utilizando, como exemplo considere as seguintes distribuições de probabilidade condicionais, para a ação $Norte$:

     \[P(\text{Agente}(x,y+1,t+1) \mid \text{Agente}(x,y,t) \land \text{Acao}(\text{Norte})) = 0.8\] \[P(\text{Agente}(x+1,y,t+1) \mid \text{Agente}(x,y,t) \land \text{Acao}(\text{Norte})) = 0.1\] \[P(\text{Agente}(x-1,y,t+1) \mid \text{Agente}(x,y,t) \land \text{Acao}(\text{Norte})) = 0.1\]

     Note que estas probabilidades somam $1.0$:

     \[\sum_{s'} P(\text{Agente}(s',t+1) \mid \text{Agente}(s,t) \land \text{Acao}(a)) = 1.0\]

     Esta é uma propriedade fundamental de qualquer distribuição de probabilidade e deve ser mantida para todas as ações do agente.

     Estas equações probabilísticas, que fogem um pouco do formalismo da lógica de primeira ordem, definem o modelo de transição estocástico para a ação $Norte$. Caberá a esforçada leitora criar modelos semelhantes para as ações $Sul$, $Leste$ e $Oeste$.

Para completar o modelo de transição, precisamos também definir o comportamento quando o agente encontra uma parede:

\[P(\text{Agente}(x,y,t+1) \mid \text{Agente}(x,y,t) \land \text{Acao}(\text{Norte}) \land \text{Estado}(x,y+1,\text{parede})) = 1.0\]

Esta equação especifica que quando há uma parede no estado de destino, o agente permanece em sua posição atual com probabilidade 1.0. Equações similares devem ser definidas para as outras direções.

A função objetivo, que guia o aprendizado do agente, também pode ser definida formalmente.

1. Recompensa Imediata: a recompensa imediata $R(x,y)$, recebida ao alcançar uma célula $(x,y)$ pode ser definida em função do tipo de célula:

   \[R(x,y) = \begin{cases} +1 & \text{se } \text{Estado}(x,y,\text{terminal}^+) \\ -1 & \text{se } \text{Estado}(x,y,\text{terminal}^-) \\ r_{\text{vida}} & \text{caso contrário} \end{cases}\]

   Esta função recompensa atribui valores diferentes dependendo se a célula é um terminal positivo, terminal negativo ou uma célula comum (vazia ou de início), utilizando a recompensa de passo $r_{\text{vida}}$. Neste caso, simplificamos a função de recompensa $R(s,a,s′)$ criando um caso especial que considera apenas a posição no mundo.

2. Função Valor: a função valor $V^\pi(x,y)$ para uma política $\pi$ pode ser definida como o valor esperado do retorno acumulado a partir do estado inicial $(x,y)$ seguindo a política $\pi$:

   \[V^\pi(x,y) = \mathbb{E} \left[ \sum_{t=0}^{\infty} \gamma^t R(x_t,y_t) \mid (x_0,y_0)=(x,y), \pi \right]\]

   Esta equação representa a definição padrão da função valor em Reinforcement Learning, agora expressa na nossa formalização em FOL.

Finalmente, o Grid World, formalizado em Lógica de Primeira Ordem, será definido por meio da tupla:

\[GW = \langle \mathcal{L}, \Sigma, M \rangle\]

Na qual, teremos:

• $\mathcal{L}$ é a linguagem de primeira ordem que definimos, incluindo os predicados $\text{Celula}$, $\text{Agente}$, $\text{Estado}$, $\text{Acao}$, $\text{Executavel}$ e $\text{Adjacente$.

• $\Sigma$ é o conjunto de axiomas do domínio que estabelecemos (Axiomas Básicos e Axiomas de Ação).

• $M$ é o modelo de transição estocástico, definido pelas probabilidades de transição para cada ação (como exemplificado para a ação $Norte$).

Este sistema, $GW$, captura formalmente a essência do Grid World utilizando Lógica de Primeira Ordem. É importante notar que este sistema preserva a propriedade de Markov, mesmo na formulação em FOL:

\[P(s_{t+1} \mid s_t, a_t, s_{t-1}, a_{t-1}, ..., s_0) = P(s_{t+1} \mid s_t, a_t)\]

Embora a linguagem de descrição seja diferente (FOL vs. notação de MDP tradicional), a propriedade de Markov, que simplifica o aprendizado, continua válida. A formalização em FOL oferece uma perspectiva alternativa ao estudo do Grid World e, por extensão, para a fundação teórica dos Processos de Decisão de Markov e do Reinforcement Learning.

O Desafio: Encontrar a Política Ótima

O objetivo central no Grid World continua sendo o mesmo: que o agente aprenda uma política ótima. Uma política é uma função que mapeia cada estado para uma ação. Uma política ótima, denotada como $\pi^∗(s)$, é aquela que, para cada estado $s$, seleciona a ação, $a$, que maximiza a soma esperada de recompensas acumuladas a partir daquele estado. A Figura 3 ilustra o conceito de política ótima e subótima, mostrando como o fator de desconto $\gamma$ pode afetar o valor das recompensas futuras.

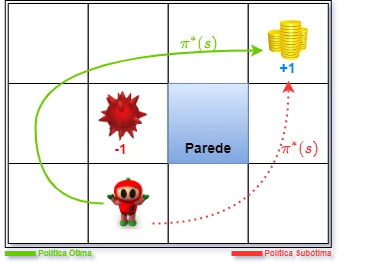
Figura 3: Ilustração da comparação entre uma política ótima e uma subótima, mostrando o efeito do fator de desconto nas recompensas ao longo do caminho.

Em nosso exemplo, um mundo de $4\times 3$ estados, o agente deve aprender a política que o guia de forma eficiente a partir do estado $Inicio$ até o estado terminal $+1$, evitando o estado terminal $-1$ e minimizando a recompensa de passo negativa acumulada ao longo do caminho. Não custa lembrar que os valores de recompensa $+1$ e $-1$ são apenas exemplos.

Próximos Passos: Solucionando o Grid World com Algoritmos de RL

Agora que definimos o Grid World tanto na perspectiva de MDP quanto na de Lógica de Primeira Ordem, o próximo passo natural é explorar como podemos usar algoritmos de Reinforcement Learning para encontrar a política ótima para um agente navegando neste ambiente. Se tudo correr bem, nas seções seguintes, investigaremos algoritmos como Programação Dinâmica, Monte Carlo, Diferença Temporal (TD) e Aprendizado por Q-Learning, e demonstraremos como eles podem ser aplicados para resolver o problema do Grid World e desvendar os segredos do Reinforcement Learning.

Resumo da Notação Utilizada

Notação Matemática

• Estados: Representados por $s$ ou $s’$. O conjunto de todos os estados possíveis é denotado por $S$.
• Ações: Representadas por $a$. O conjunto de ações possíveis é denotado por $A$.
• Função de Transição: Denotada por $P(s’ \vert s, a)$, que representa a probabilidade de transitar para o estado $s’$ ao tomar a ação $a$ no estado $s$.
• Função de Recompensa: Denotada por $R(s, a, s’)$, que mapeia cada par estado-ação para um valor numérico representando a recompensa imediata.
• Política: Denotada por $\pi(s)$, que mapeia estados para ações. A política ótima é denotada por $\pi^*(s)$.
• Função Valor: Denotada por $V^\pi(s)$, que representa o valor esperado de longo prazo de estar em um estado $s$ seguindo a política $\pi$.

Notação em Lógica de Primeira Ordem (FOL)

• Predicados:
  • $\text{Celula}(x, y)$: Verdadeiro se $(x, y)$ é uma célula válida na grade.
  • $\text{Agente}(x, y, t)$: Verdadeiro se o agente está na célula $(x, y)$ no instante $t$.
  • $\text{Estado}(x, y, tipo)$: Define o tipo de célula na posição $(x, y)$.
  • $\text{Acao}(a)$: Verdadeiro se $a$ é uma ação válida.
  • $\text{Executavel}(a, x, y)$: Verdadeiro se a ação $a$ é executável a partir da célula $(x, y)$.
  • $\text{Adjacente}(x, y, x’, y’, a)$: Verdadeiro se $(x’, y’)$ é adjacente a $(x, y)$ na direção da ação $a$.
• Axiomas:
  • Axioma 1: Tipo de célula único.
  • Axioma 2: Posição única do agente.
• Modelo de Transição:
  • Probabilidades de transição são representadas por $P(\text{Agente}(x’, y’, t+1) \mid \text{Agente}(x, y, t), \text{Acao}(a))$.

Exemplos de Uso

• Função de Transição:

  \[P(s' \vert s, a) = \text{Probabilidade de transitar para } s' \text{ ao tomar a ação } a \text{ no estado } s\]

• Função de Recompensa:

  \[R(s, a, s') = \text{Recompensa imediata ao transitar de } s \text{ para } s' \text{ após executar a ação } a\]

• Política:

  \[\pi(s) = \text{Ação a ser tomada no estado } s\]

• Função Valor:

  \[V^\pi(s) = \mathbb{E} \left[ \sum_{t=0}^{\infty} \gamma^t R(s_t) \mid s_0 = s, \pi \right]\]